Transformer Model

Transformer components

Challenging language understanding(NLP 问题)

Long term dependency:
1. e.g.指代消岐：我的书柜太宽了，而且非常重，我没有办法把它搬出书房，“它”的指代是？
2. 解决方法：Attention
Sophisticated meaning:
1. e.g. 多重否定：我原以为这部电影挺无聊的，没想到还不错，“原以为”，“无聊”，“没”，“还不错”
2. 解决方法：Feed Forward network
Word order matters a lot:
1. e.g. 词语顺序敏感：屡败屡战，屡战屡败
2. 解决方法：Position encoding

Key module: attention layer for long-term interaction

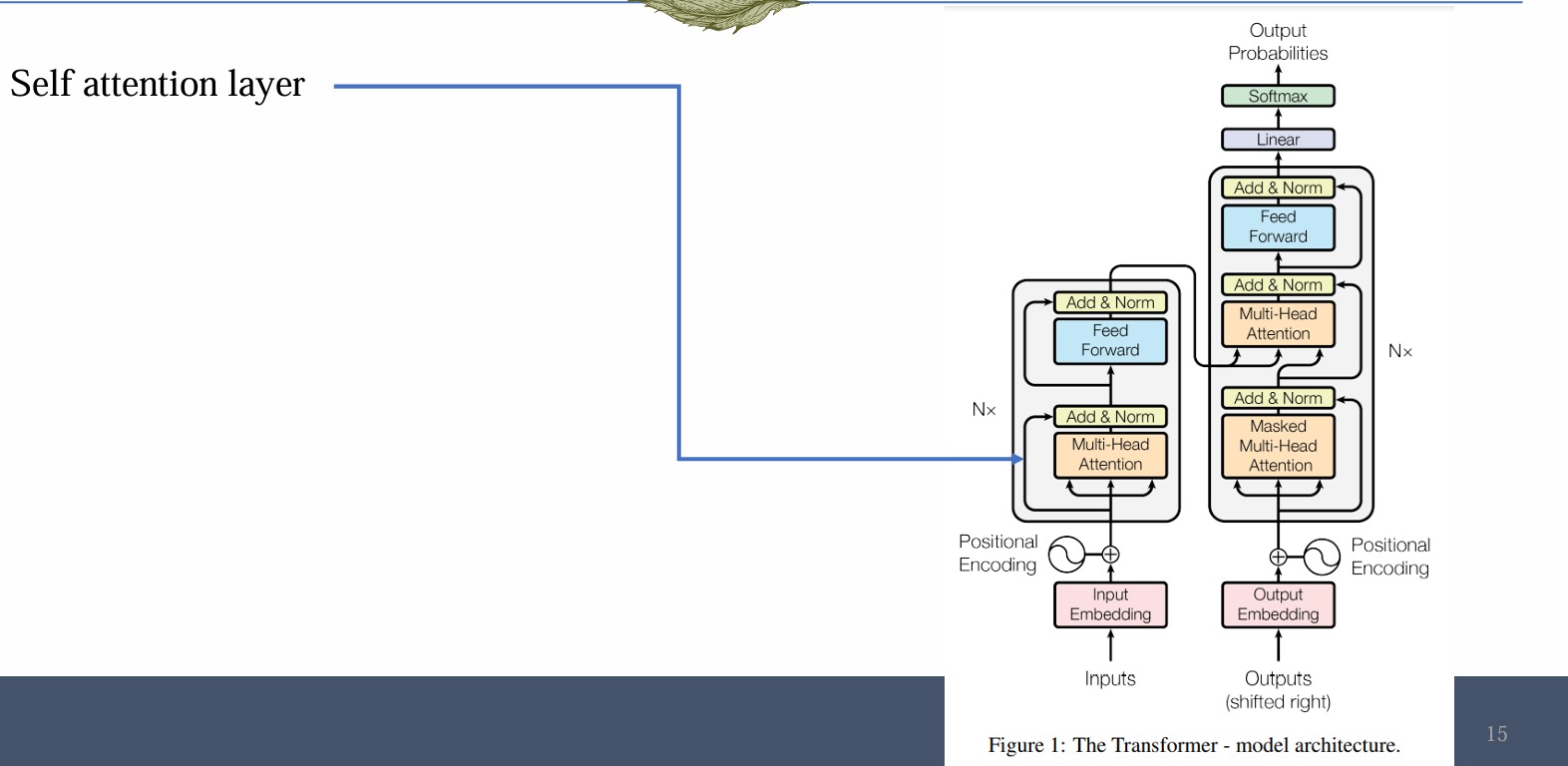
假设词有独立含义，可以用有语义信息的向量表示(本质上是word embedding)
Attention的作用：已知词含义，求每个词在上下文关联中的含义
1. 输入：n个词向量，输出：n个基于上下文理解的含义[x1,x2,…,xn] -> [z1,z2,…,zn]
2. 希望zi在包含自身含义时还包含其他信息，比x更多更准的信息：
  1. 必须收集有选择性的信息
  2. 不同词不同上下文，选择方法和范式不同

How to understand attention?

哈希表：由(keys, value)对组合构成，判断 k 和 q 是否完全对应
1. 若完全对应，则返回 v
2. 若不完全对应，则返回空
Attention 可以理解为 soft version 的哈希表：
1. 不考察 k 和 q 是否完全对应，而是考察二者的相关性，决定线性加权系数
2. 不直接返回 v ，而是根据相关性进行 v 的线性组合，返回线性组合计算结果
输入每个词的词向量 xi ，首先根据矩阵 Wq , Wk , Wv 计算出每个词的 qi , ki , vi
每个词的 qi 要和所有的 ki 作用(点乘，本质上是计算相关程度)，计算长序列每两个词的相似性
点乘结果需要 ÷√dk 得到 score ，÷√dk 因为点乘值可能很大，训练不稳定：期望为0，但是方差不为0(为dk)，导致score很大，softmax后可能为0或者1，不利于学习
得到 qi·kj/√dk 后经过 softmax 得到 xij

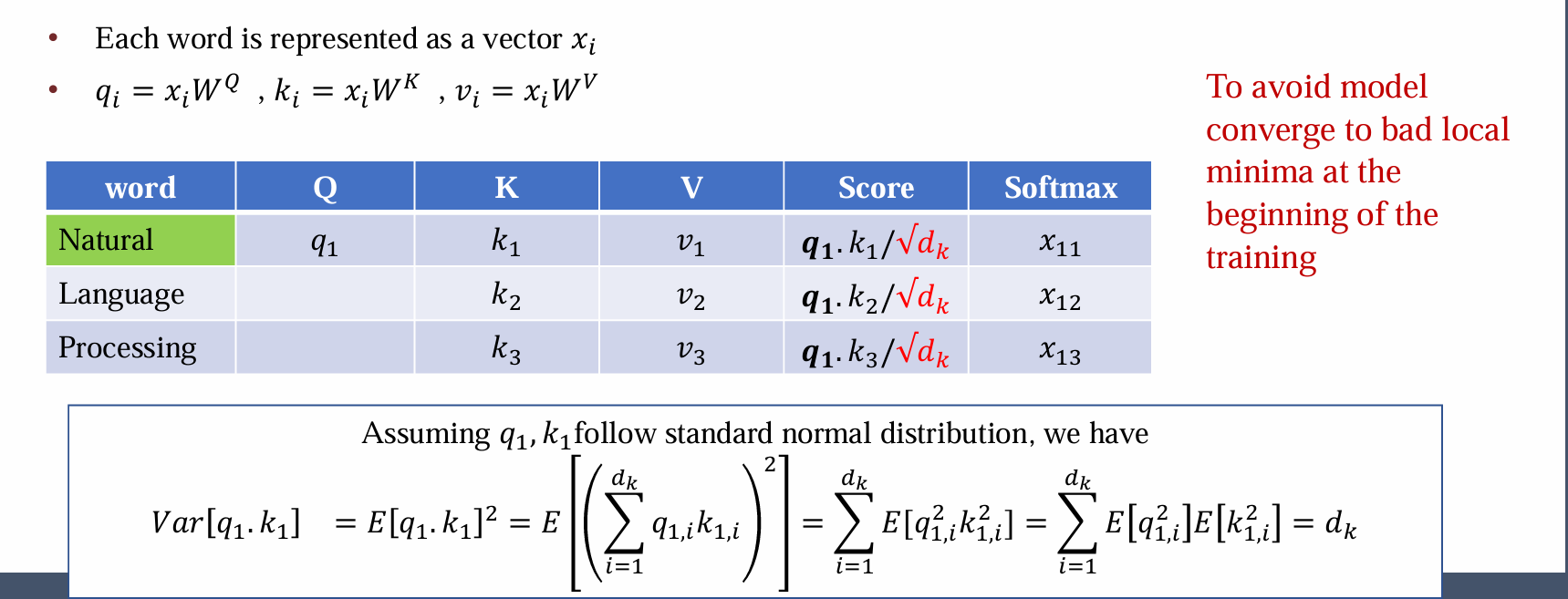
xij 实质上线性加权的权重，其构成的矩阵称之为注意力矩阵 A ，然后再与 v 作用得到最后的输出 zi

同理计算每个词向量，可得[z1,z2,…,zn]：

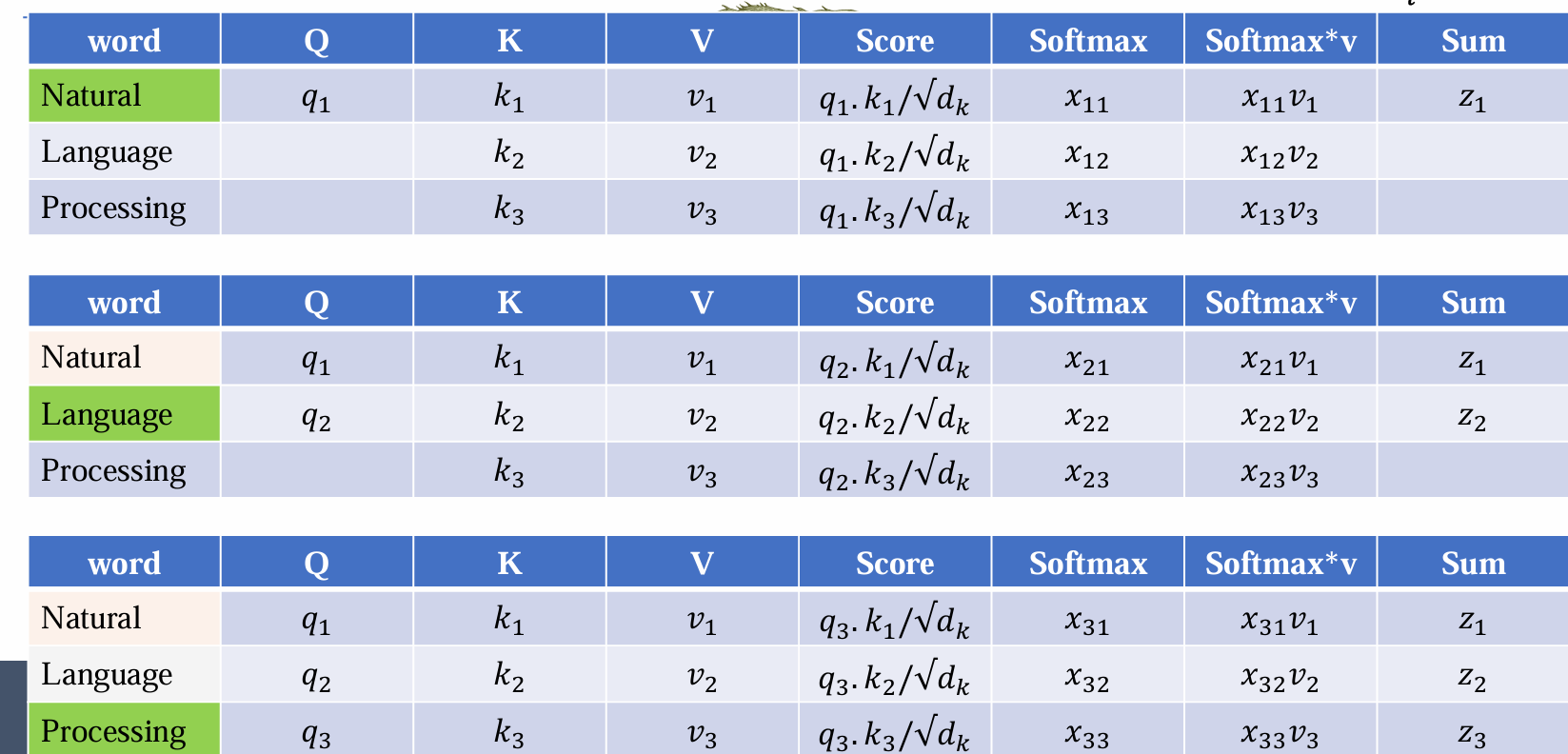
The compact form of attention

问题：代码不能按照如上方式实现，需要进一步优化
attention的输入：X = [x1,x2,…,xn]，每个词都对应的d的vector，X ∈ Rnxd
1. 对于第一层attention，𝑋 由词word embedding组成
2. 对于中建城attention，X 由前一层的输出结果组成
构建 Q , K , V： 𝑄 = 𝑋𝑊q ∈ 𝑅𝑛×𝑑𝑘, 𝐾 = 𝑋𝑊k, 𝑉 = 𝑋𝑊v
计算相关矩阵： 𝐸 = 𝑄𝐾𝑇/√𝑑 ∈ 𝑅𝑛×𝑛
1. 每两个 vector 都需要计算 correlation
2. Q 是 nxd 维，K 是 nxd 维，Q·K.T 得到 nxn 矩阵
3. 第i行第j列描述了第i个query和第j个key的相似程度
归一化相关矩阵：𝐴 = 𝑠𝑜𝑓𝑡𝑚𝑎𝑥(𝐸)
线性组合得到输出： output = 𝐴v
以上操作都为矩阵乘法，均可并行加速

Multi-head attention

每个 head 都有不同的自己的 𝑊q, 𝑊k, 𝑊v，从而增加了数据量和模型复杂程度
线性组合得到输出：output = 𝑐𝑜𝑛𝑐𝑎𝑡𝑒 [𝐴𝑉]
代码实现如下：

def multi_head_attention_forward(
    query: Tensor,
    key: Tensor,
    value: Tensor,
    embed_dim_to_check: int,
    num_heads: int,
    in_proj_weight: Tensor,
    in_proj_bias: Tensor,
    bias_k: Optional[Tensor],
    bias_v: Optional[Tensor],
    add_zero_attn: bool,
    dropout_p: float,
    out_proj_weight: Tensor,
    out_proj_bias: Tensor,
    training: bool = True,
    key_padding_mask: Optional[Tensor] = None,
    need_weights: bool = True,
    attn_mask: Optional[Tensor] = None,
    use_separate_proj_weight: bool = False,
    q_proj_weight: Optional[Tensor] = None,
    k_proj_weight: Optional[Tensor] = None,
    v_proj_weight: Optional[Tensor] = None,
    static_k: Optional[Tensor] = None,
    static_v: Optional[Tensor] = None,
) -> Tuple[Tensor, Optional[Tensor]]:


    attn_output_weights = torch.bmm(q, k.transpose(1, 2))
    assert list(attn_output_weights.size()) == [bsz * num_heads, tgt_len, src_len]

    if attn_mask is not None:
        if attn_mask.dtype == torch.bool:
            attn_output_weights.masked_fill_(attn_mask, float("-inf"))
        else:
            attn_output_weights += attn_mask

    if key_padding_mask is not None:
        attn_output_weights = attn_output_weights.view(bsz, num_heads, tgt_len, src_len)
        attn_output_weights = attn_output_weights.masked_fill(
            key_padding_mask.unsqueeze(1).unsqueeze(2),
            float("-inf"),
        )
        attn_output_weights = attn_output_weights.view(bsz * num_heads, tgt_len, src_len)

    attn_output_weights = softmax(attn_output_weights, dim=-1)
    attn_output_weights = dropout(attn_output_weights, p=dropout_p, training=training)

    attn_output = torch.bmm(attn_output_weights, v)
    assert list(attn_output.size()) == [bsz * num_heads, tgt_len, head_dim]
    attn_output = attn_output.transpose(0, 1).contiguous().view(tgt_len, bsz, embed_dim)
    attn_output = linear(attn_output, out_proj_weight, out_proj_bias)

    if need_weights:
        # average attention weights over heads
        attn_output_weights = attn_output_weights.view(bsz, num_heads, tgt_len, src_len)
        return attn_output, attn_output_weights.sum(dim=1) / num_heads
    else:
        return attn_output, None

严格来说 attention 是非线性，因为 softmax 操作是非线性的
但是非线性不多，attention 的功能主要在于收集和组织可以看到上下文信息的数据，功能类似于线性

Key module: FFN (feed-forward network)

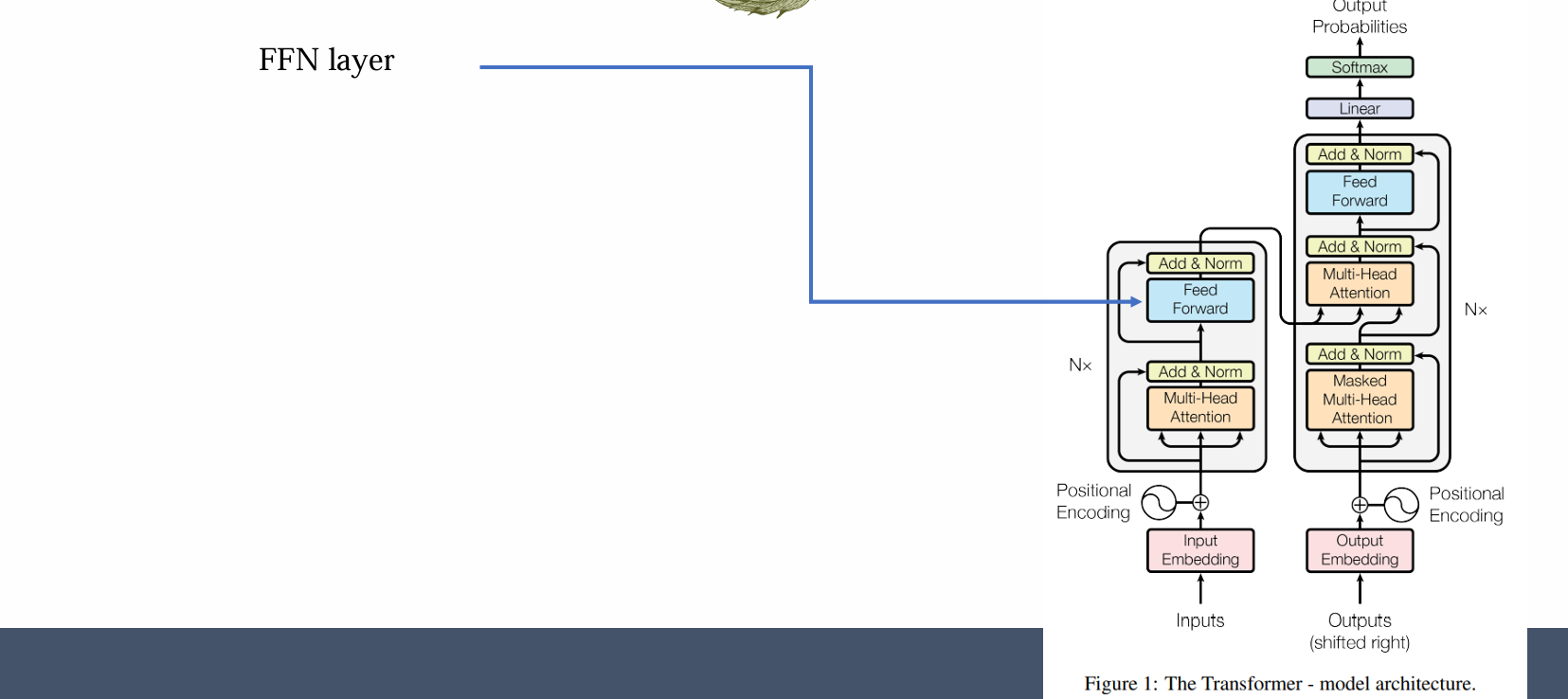
问题：现在的信息只是手机和组织，但是并不能处理复杂的信息，还需进一步整合信息以理解语言的复杂性
FFN 输入: attention output zi
𝐹𝐹𝑁 (𝑧𝑖) = 𝑊²𝜎(𝑊𝑧𝑖)
𝜎 是非线性函数，通常使用GeLU，GeLU在0附近可导:

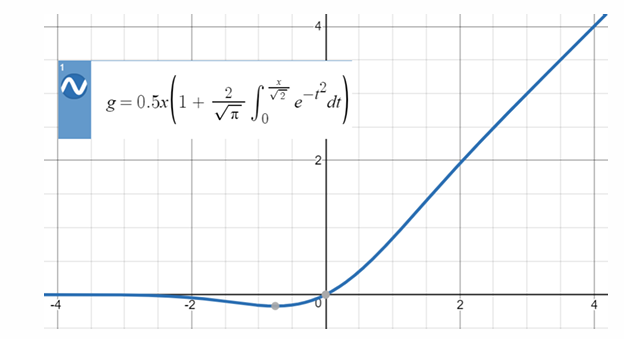
𝜎(𝑊𝑧𝑖)中的 W 是 hidden layer，通常非常大
在各个位置独立处理：

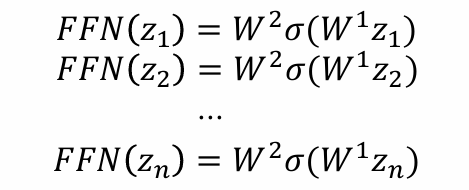
Residual connection

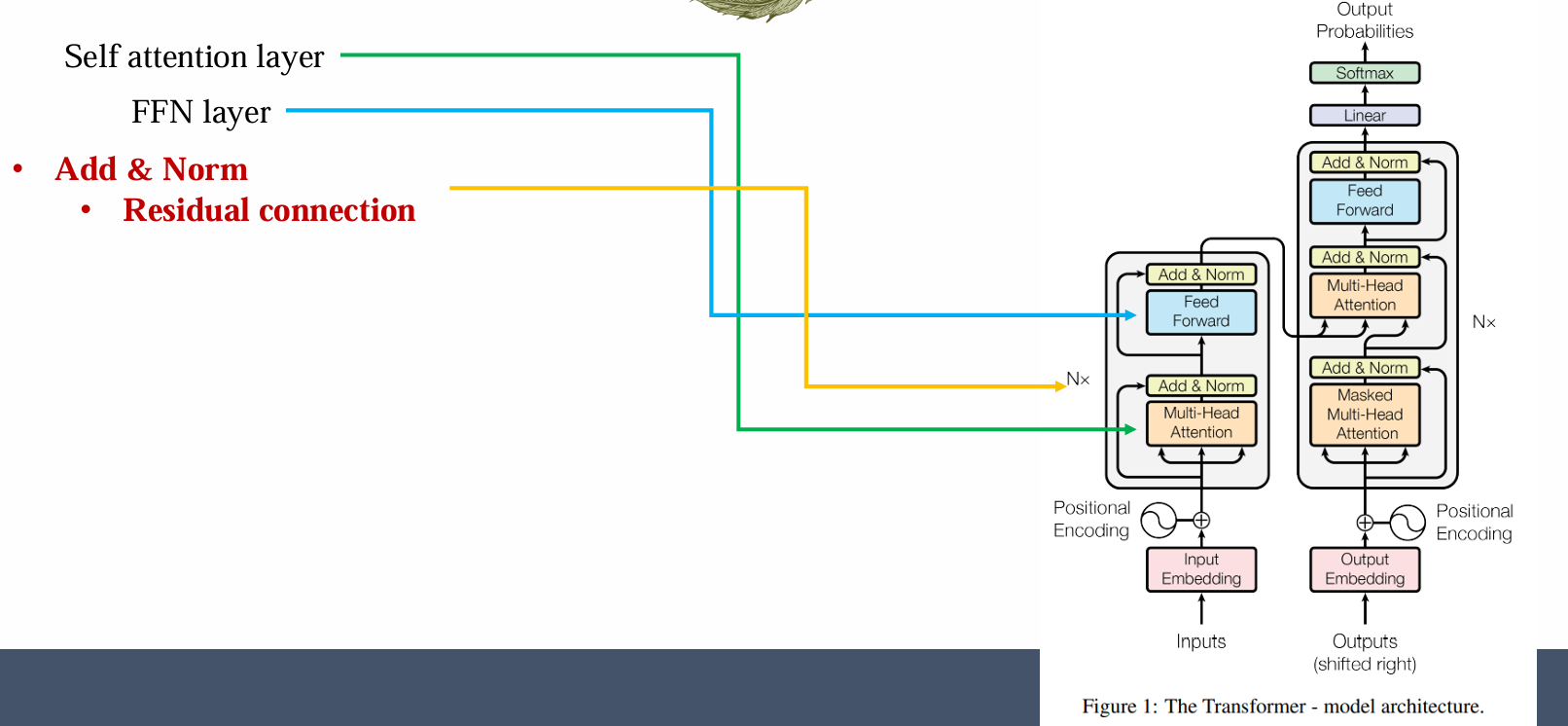
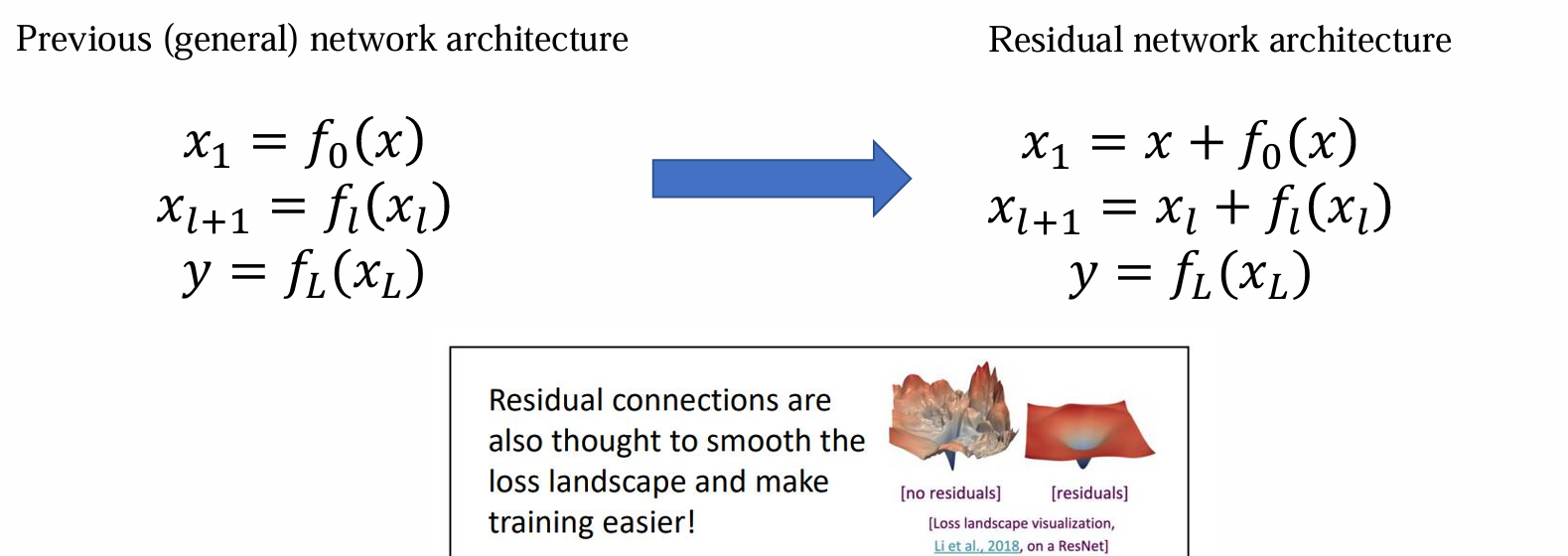
使用 residual connection 可以带来更好的优化效果

Layer normalization

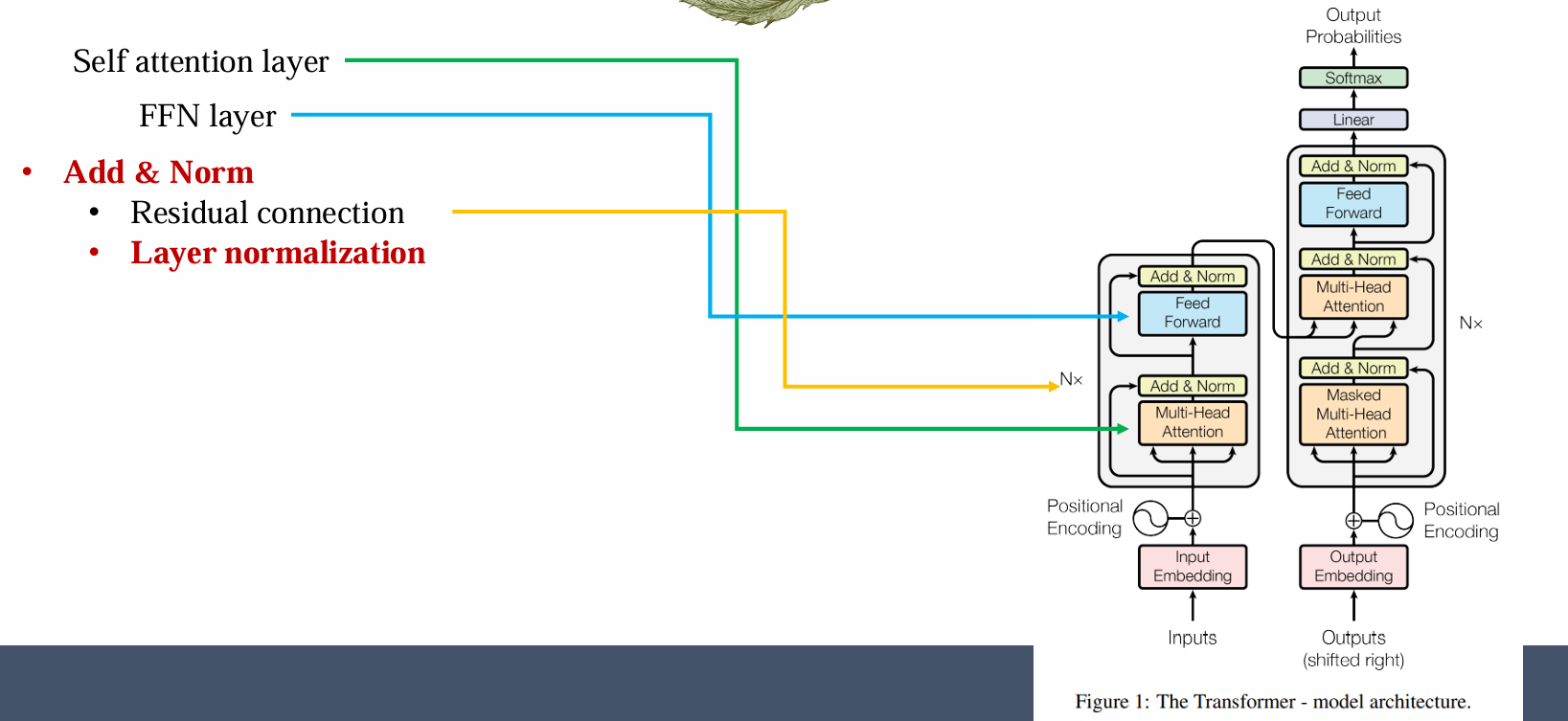
应该着重注意 layer normalization:
1. 很多 paper 和 code 的 layer normalization 是不一致的
2. 很容易出现 bugs
变量的呈现方式是 tensors:
1. 输入：x
2. 中间变量：zi
tensor 比矩阵要多一维度：batch_size * sequence_length * embed_dim
T[i][j][k]:第 i 句的第 j 个 token 的第 k 维的值
T[i][j][:]:隐去第 k 维，第 i 句的第 j 个 token 的 embedding vector
T[:][j][k]:隐去第 i 维，都取第 j 个 token 的第 k 维
不同的归一化方法沿不同维度计算均值和方差，但公式相同：

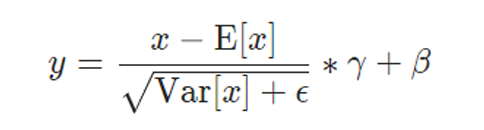
Layer normalization: 沿着 embedding 维度归一化，对每一个 batch 中的(sentence, position)对：
1. 获取(中间层)的embedding
2. 计算其均值和方差
3. 对 embedding 层进行归一化

Transformer vaiants

Two different structures

问题：如何组织这些部分组件，前后顺序应该是怎样的
现在常见的 transformer 通常有两种结构：

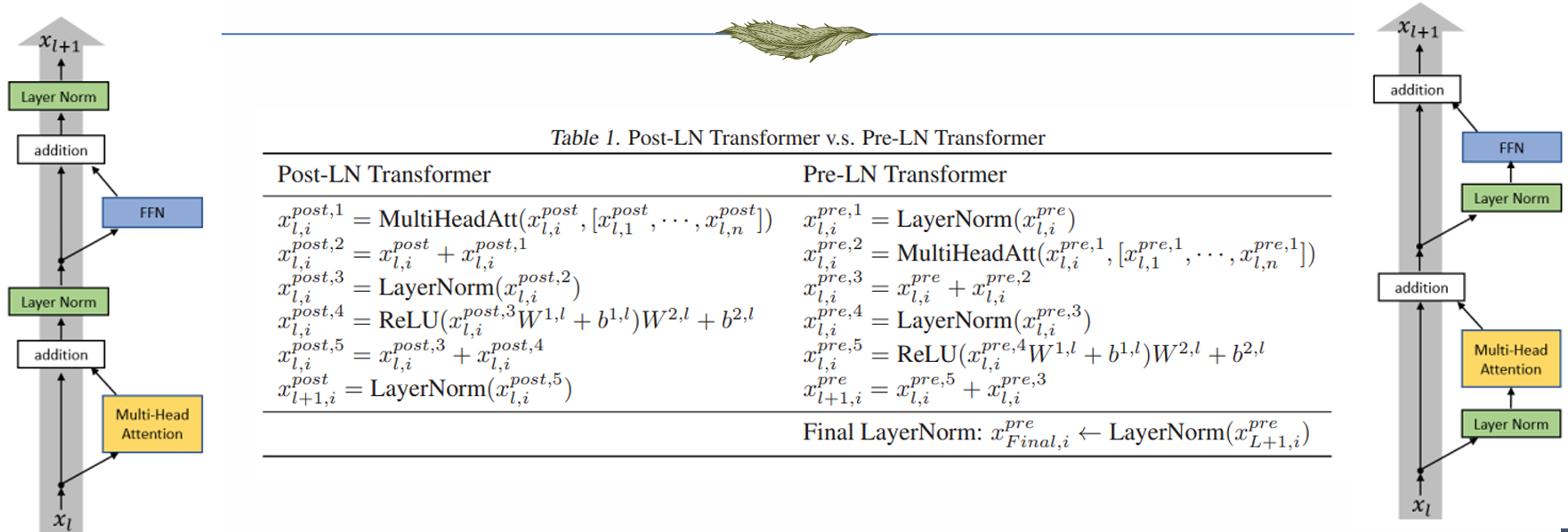
区别：输入是否可以“直通”输出，是否存在非线性
右侧结构输入可以“直通”输出，而左侧的结构优化不稳定

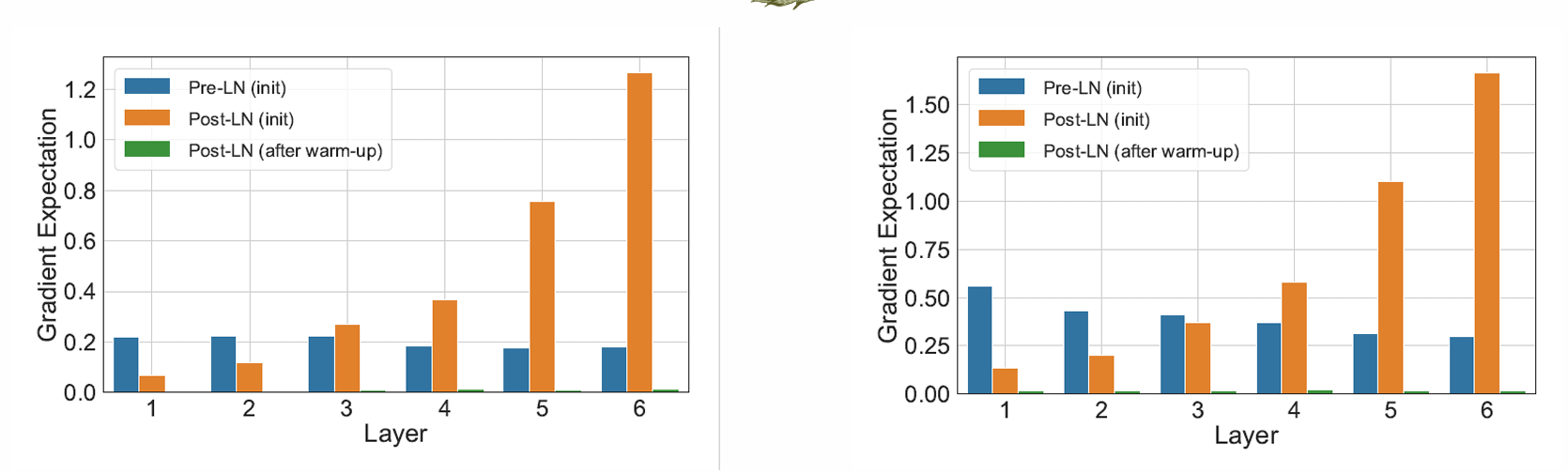
Unstable training of Post-LN Transformer

Transformer 在大多数序列任务中都取得了优异的表现。但是在成功的背后 transformer 的训练是非常不稳定并且需要很多技巧的
训练需要：big data + big model + 对超参数选择极其敏感
优化 transformer 非常困难，因为 transformer 的 lr decay 函数非常敏感，会造成训练不稳定
transformer 的 lr 需要预热阶段，从小增大再减小，且高点极其敏感

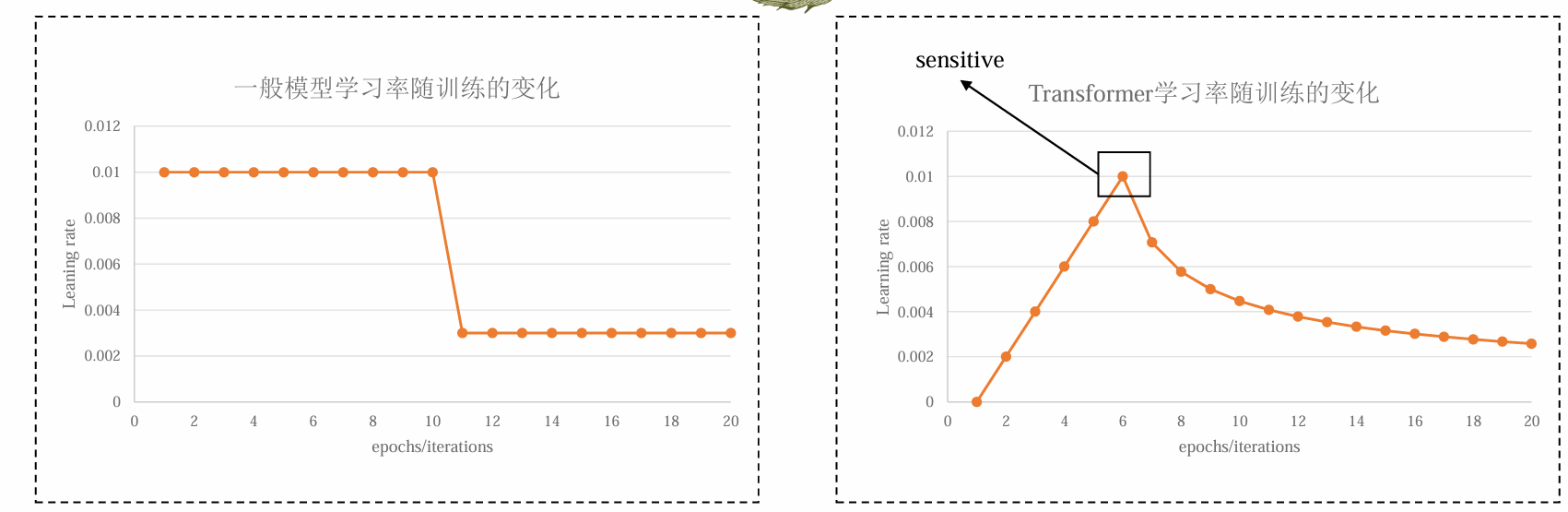
Stable training of Pre-LN Transformer

而右侧结构无上述问题，原因：梯度分布值较为一致

Key module: positional encoding

位置编码常见有三种：绝对位置编码、相对位置编码、旋转位置编码
绝对位置编码：
1. 位置中的词向量xi
2. 位置中的位置编码pi
3. 输入到第一层 transformer layer 中为 xi + pi

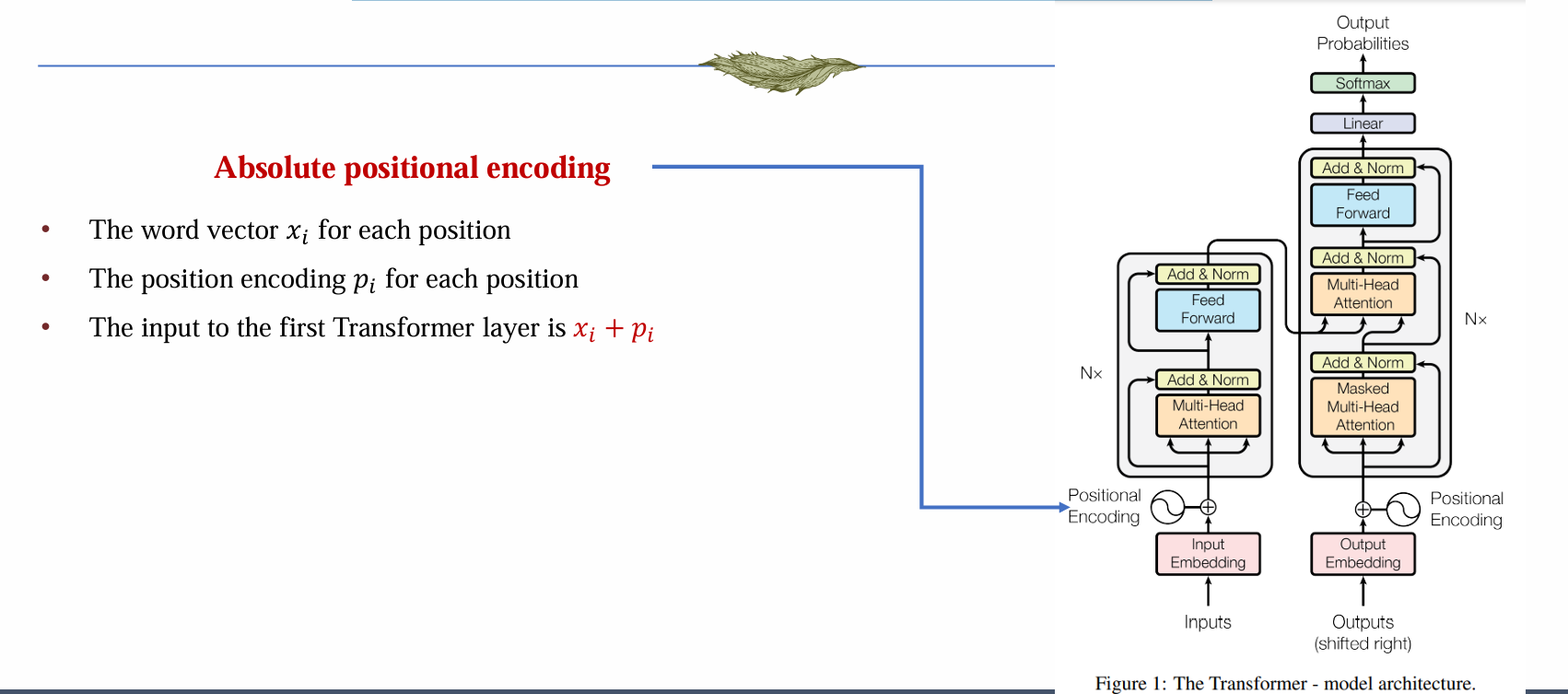
pi 被设置为可训练的参数

问题：
1. 经过 Wq 和 Wk 作用后的位置编码已经和相对位置无关
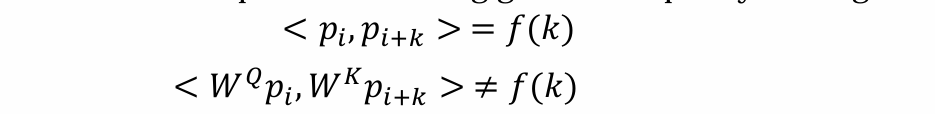
2. 可学习的绝对位置编码无法用于长序列中，因为没有见到过
3. 绝对位置编码无法扩展到更复杂的场景中(e.g. image没有绝对位置的概念)
相对位置编码：对每两个位置之间的相对距离进行编码 bij = f(i - j)
相对位置编码可以大大缓解前面提到的问题

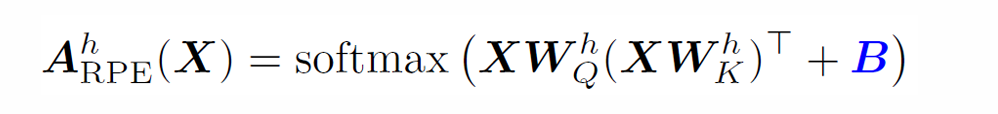
其中 B 考虑到位置相关性，B 矩阵是对称矩阵。e.g. T5

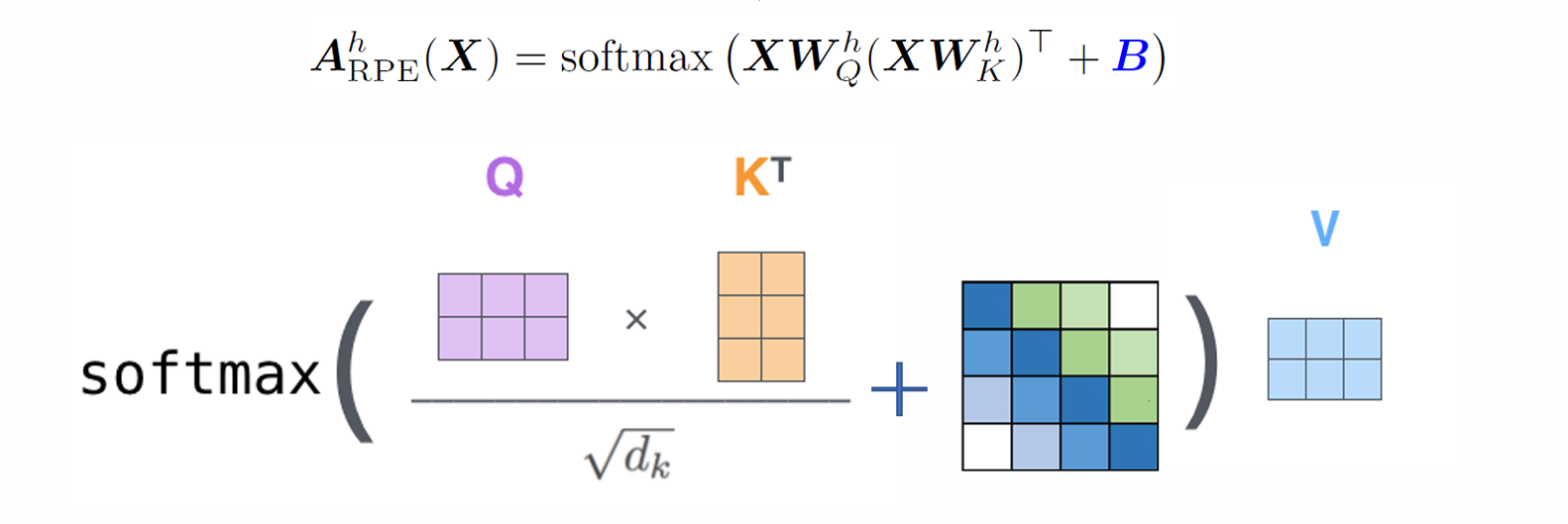
旋转位置编码：通过旋转矩阵对每两个位置之间的相对距离进行编码。本质上把矩阵加法变成矩阵乘法