智能机器人概论 07 运动控制
运动控制 Motion Control
基本概念
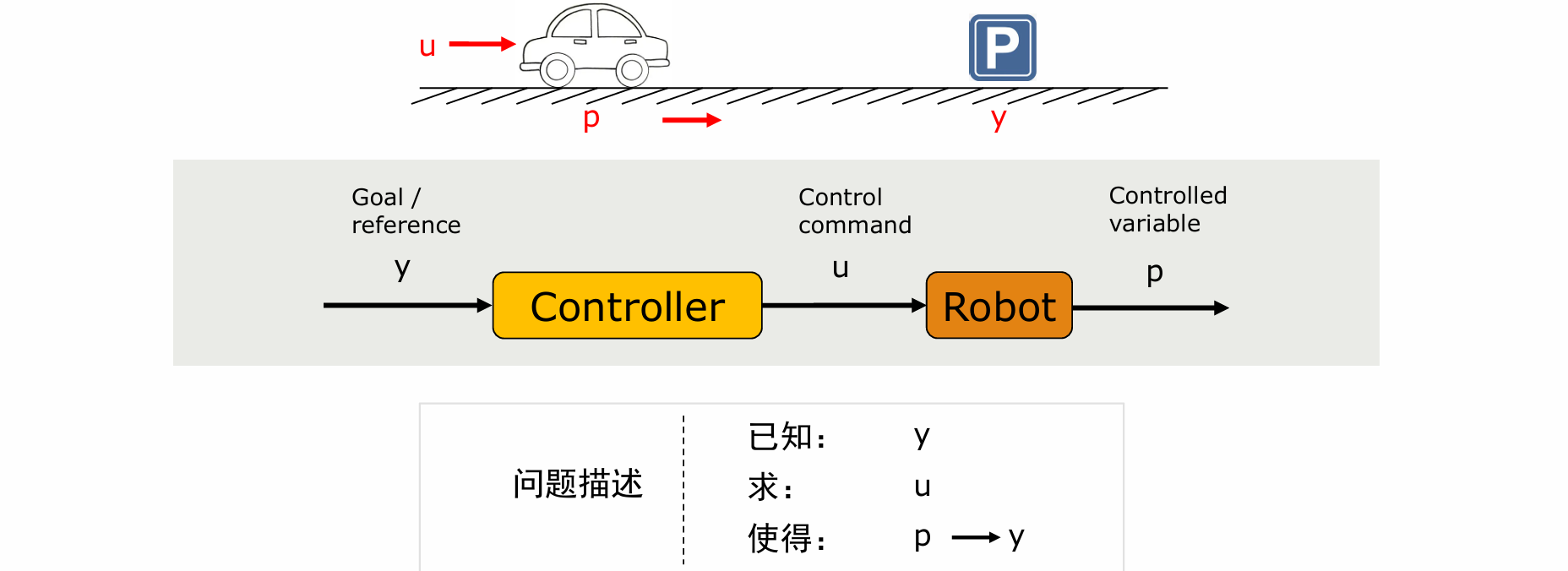
- 开环控制–Open-Loop Control
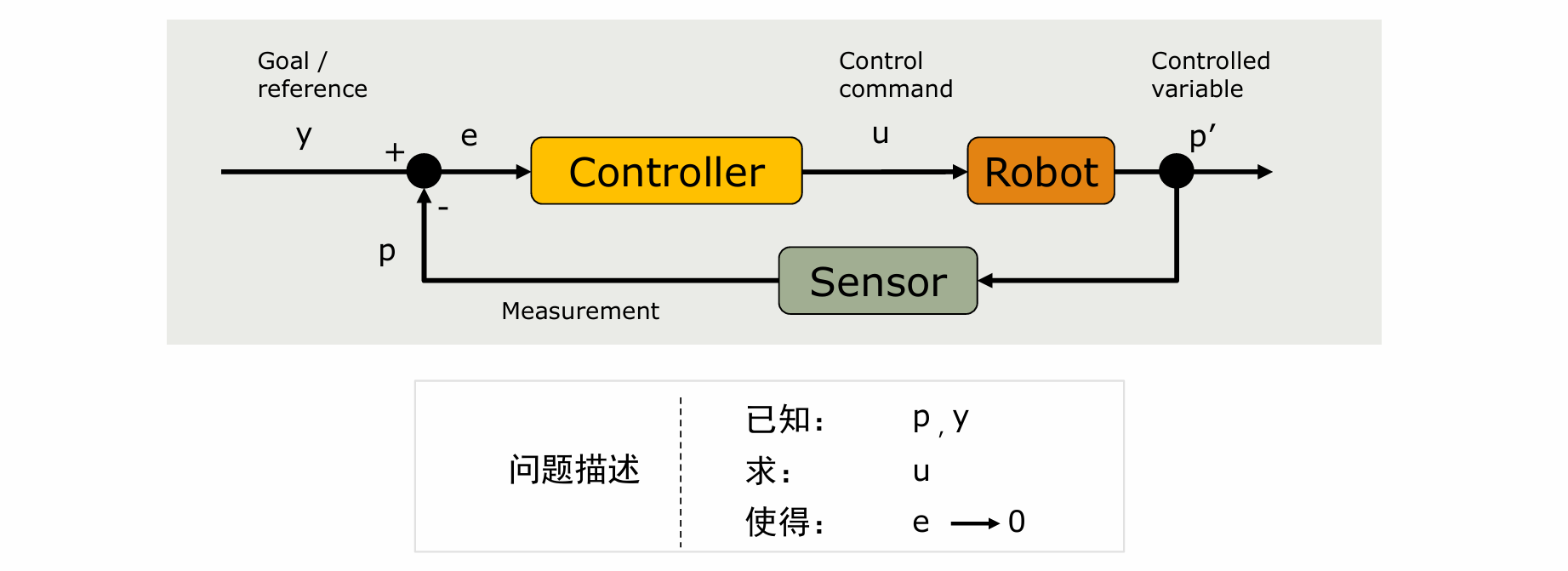
- 闭环控制–Close-Loop Control,也称为反馈控制(Feed-back Control)
- 运动控制方法分类:
- 黑箱控制Black-box Control:PID Control
- 几何控制Geometric Control:Pure Pursuit Control
- 优化控制Optimal Control:MPC Control
- 基于学习的控制Learning-based Control:End-to-end Control
黑箱控制 Black-box Control– PID Control
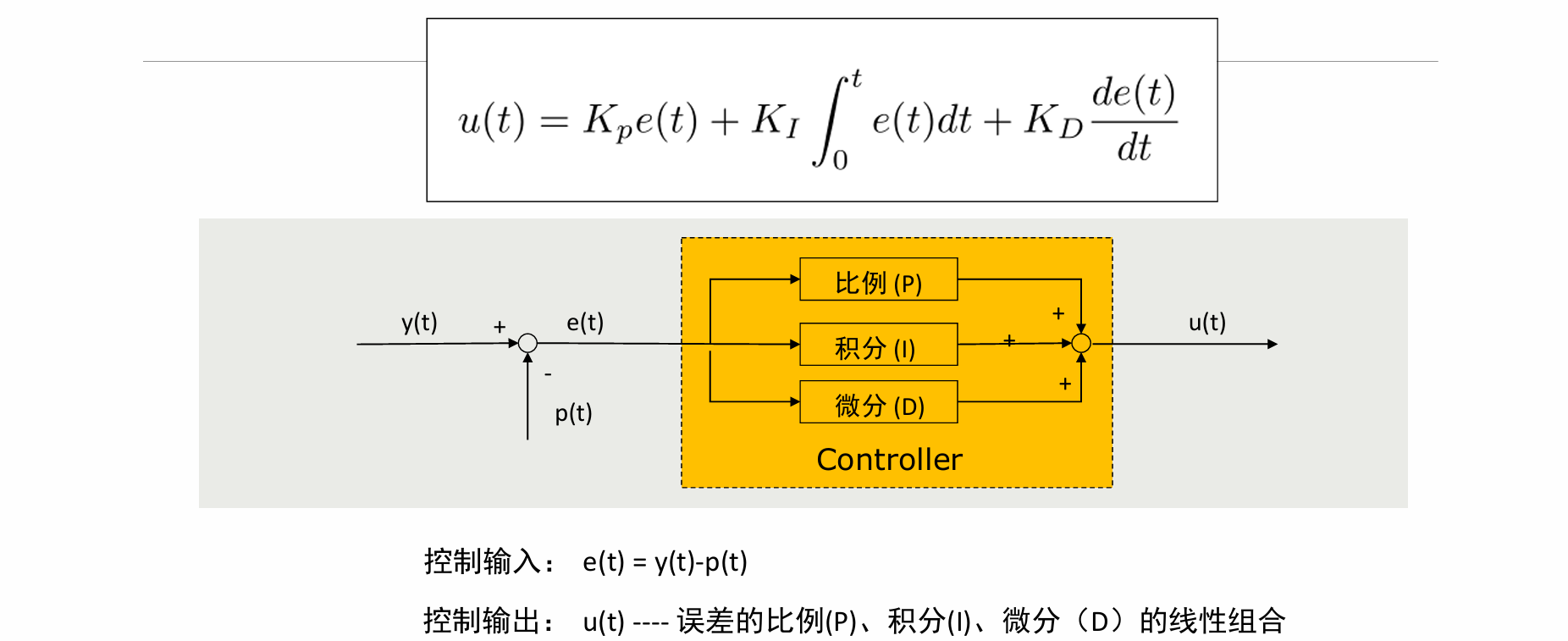
u(t) 是控制量,e(t) 是误差,积分项是过去误差的累积,微分项是误差变化的趋势
问题:需要微调Kp、Ki、Kd
P控制–比例(Proportion)
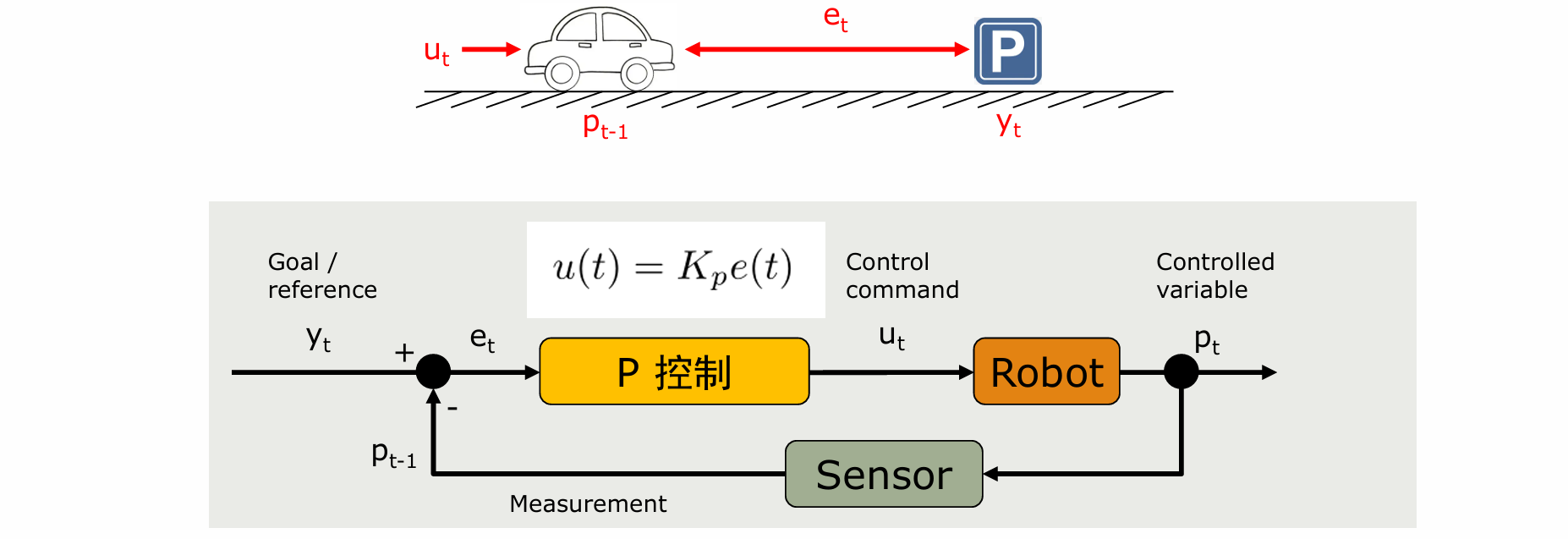
- 比例控制局限性:u低于机器人驱动敏感区间的下界є后,机器人与目标保持et而不可达。误差小的时候不敏感
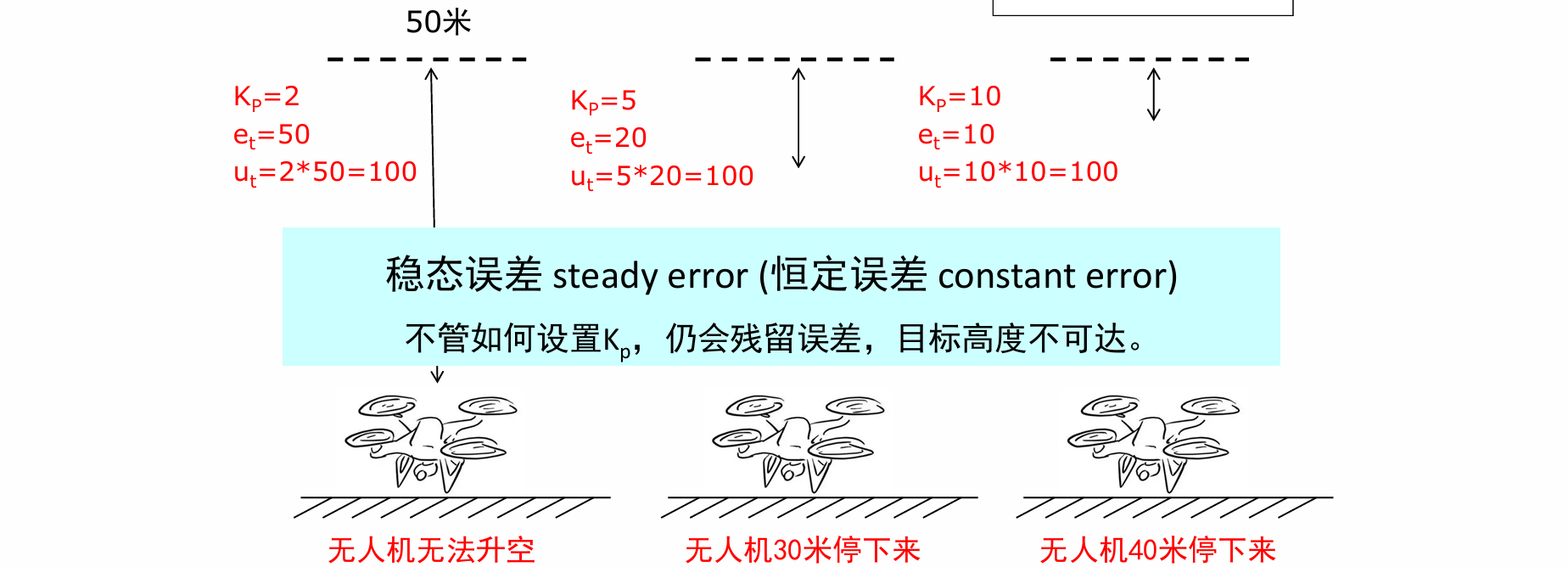
- 解决方法:加入误差累积,使得e(t)累积进入敏感状态
PI控制–积分(Integration)
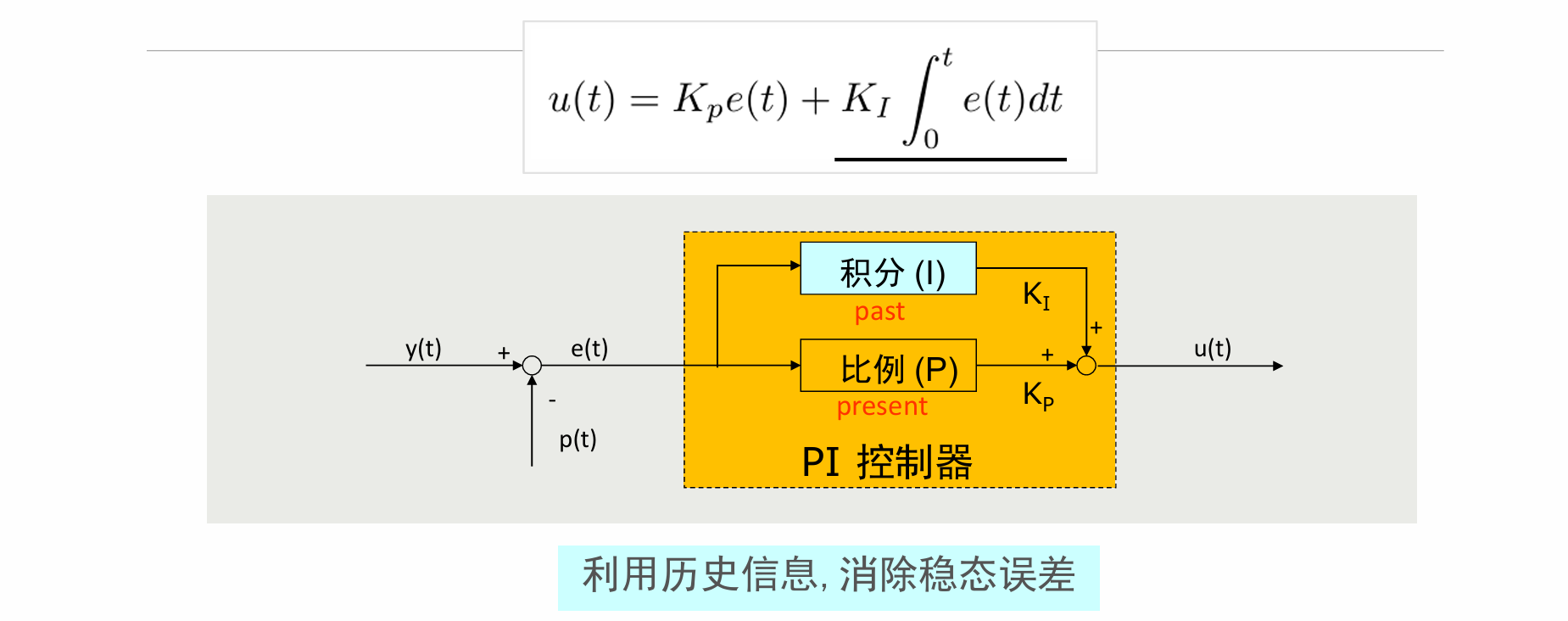
- 积分控制的局限性:到达目标的过程中会发生超调,震荡严重(overshoot)

- 解决方法:为了减少震荡,控制器不仅需要看到过去(I)和现在(P),还需要看到将来(D),具有预测能力
PID控制–微分(Derivative)
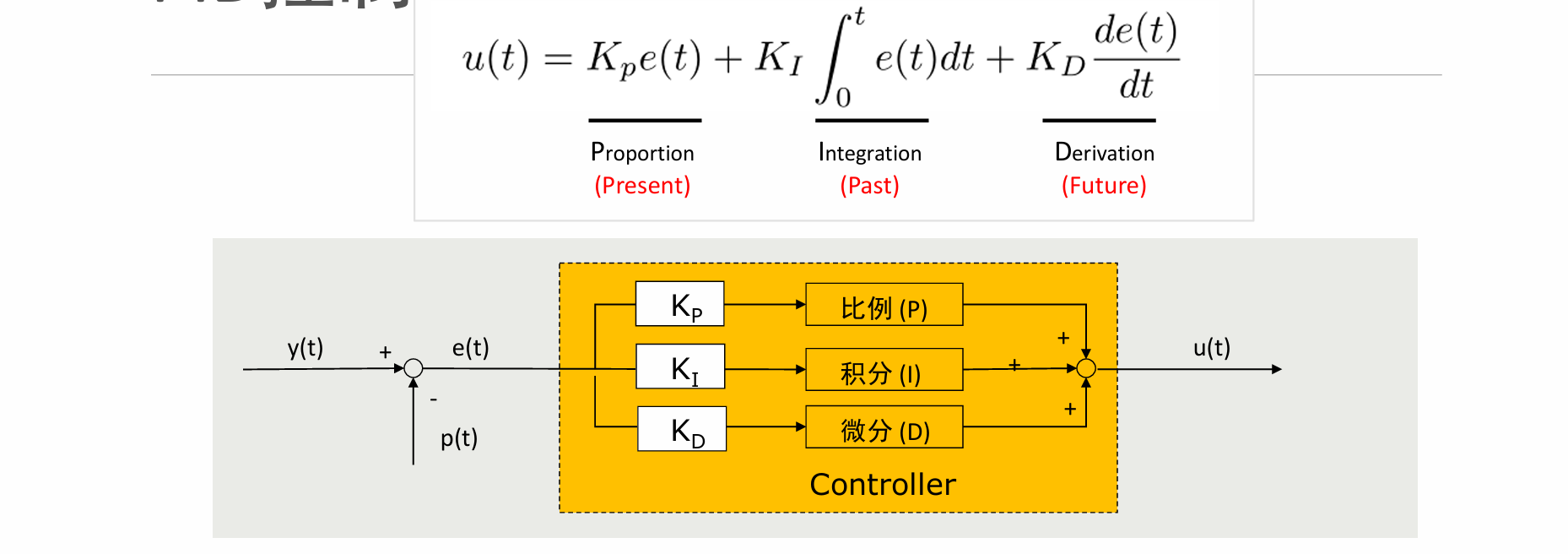
黑盒控制:无需知道过程的知识
方法简单实用:P、I、D的线性组合,依赖调参:KP、KI、KD极大地影响着算法性能
运动学模型 Kinematics Model (Car-like Robot)
类车机器人的运动学 Kinematics of a Car-like Robot
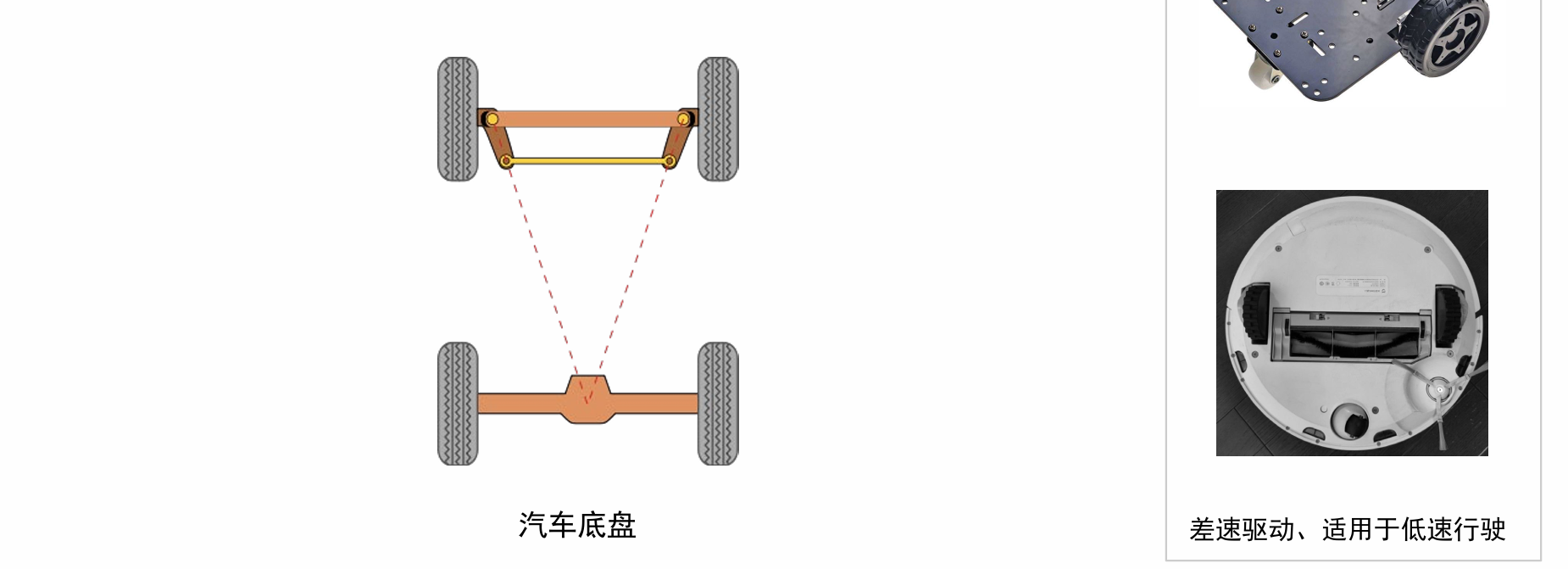
阿克曼转向模型 Ackerman Steering Model
- 基本思想:车体上所有店都是围绕一个共同的圆心运动,这种状态是最稳定的控制状态
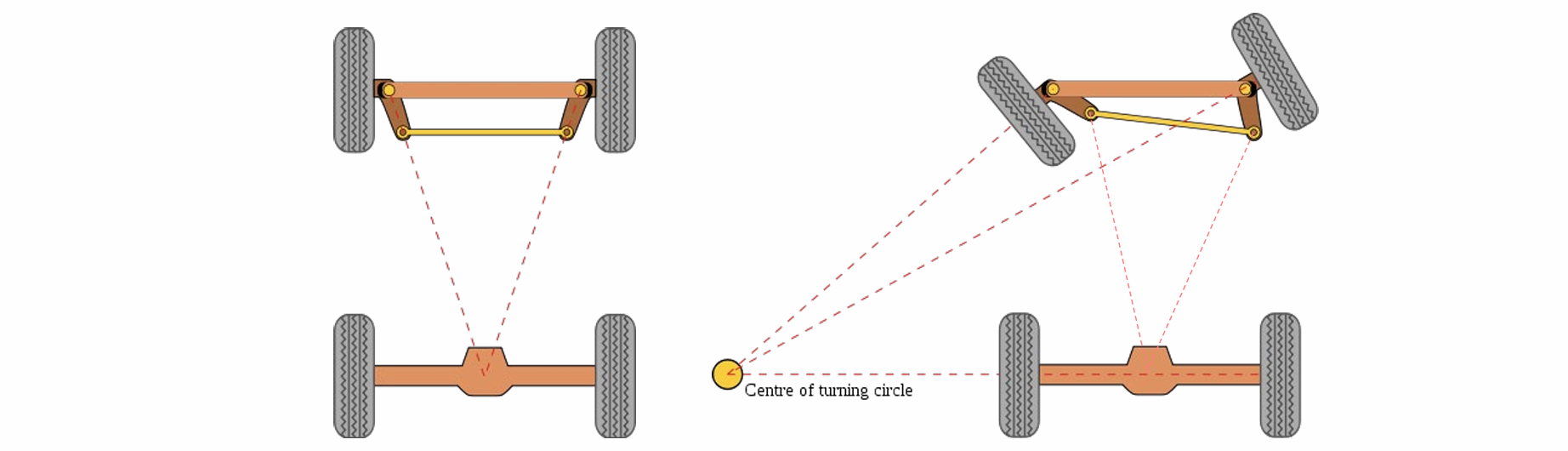
- 通过轮中心点围绕共同圆心运动可得Bicycle Model自行车模型:
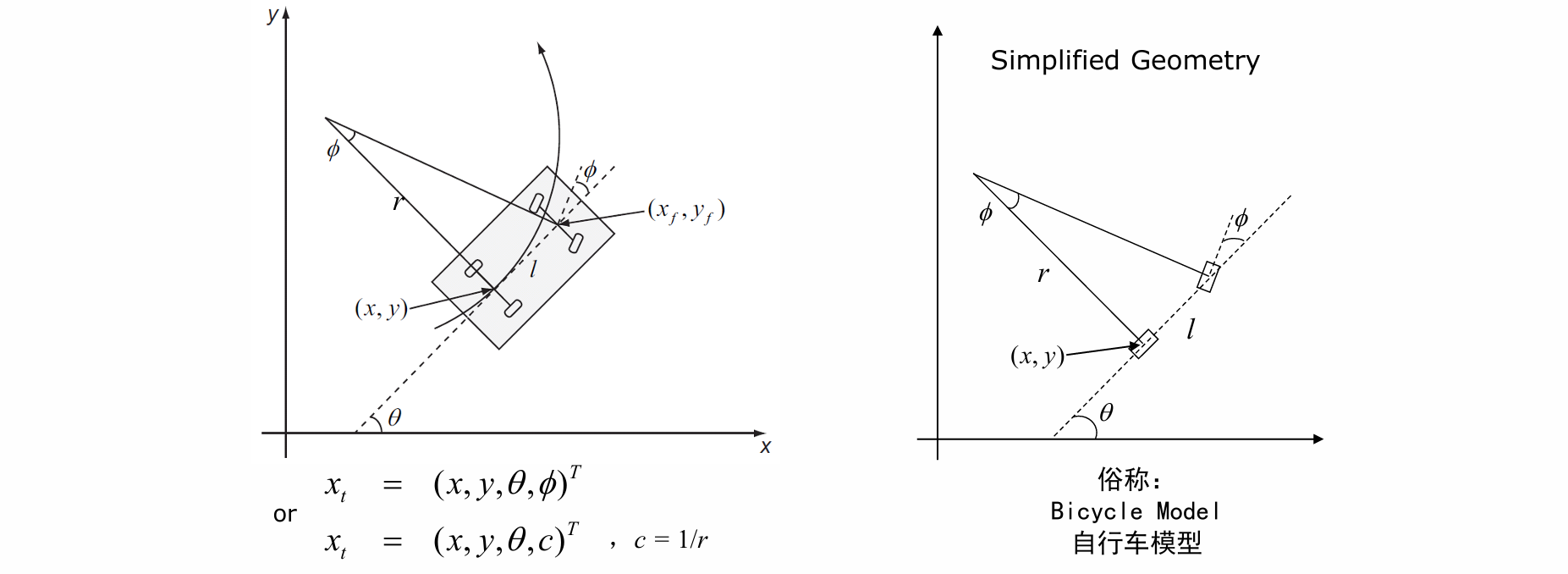
- 正运动学:
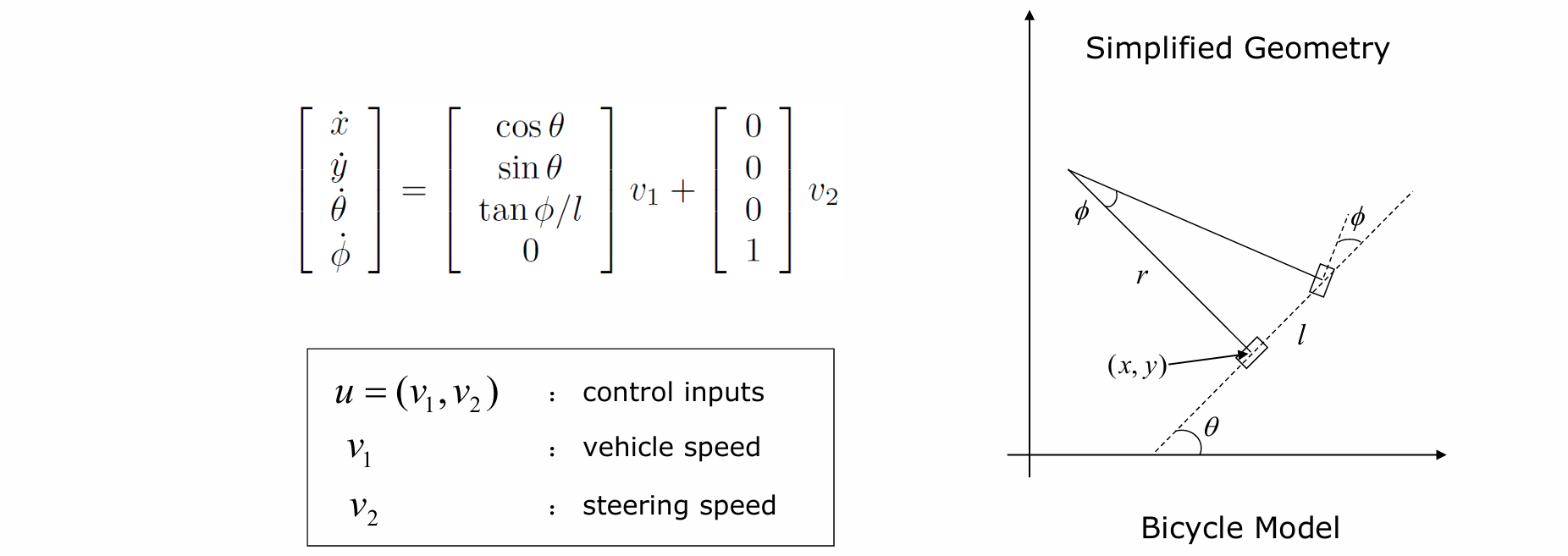
- 逆运动学:

控制集 Control Set
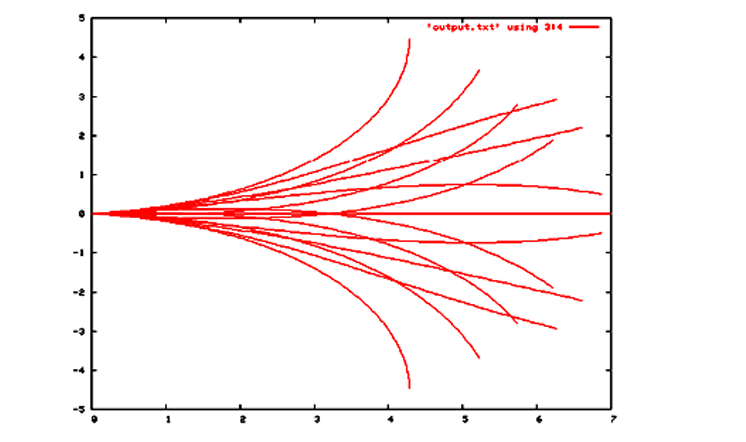
在有限时间窗口T执行控制命令u完成一次运动,获得轨迹Pu,称为控制基元Control Primitive
在控制命令空间中进行采样,获得的轨迹集合{Pu}为控制集
控制集描述了机器人在时间窗口T内可完成的所有运动及可到达的所有状态
控制集可以离线生成,标定控制集是准确控制的基础
几何控制 Geometric Control – Pure Pursuit Control
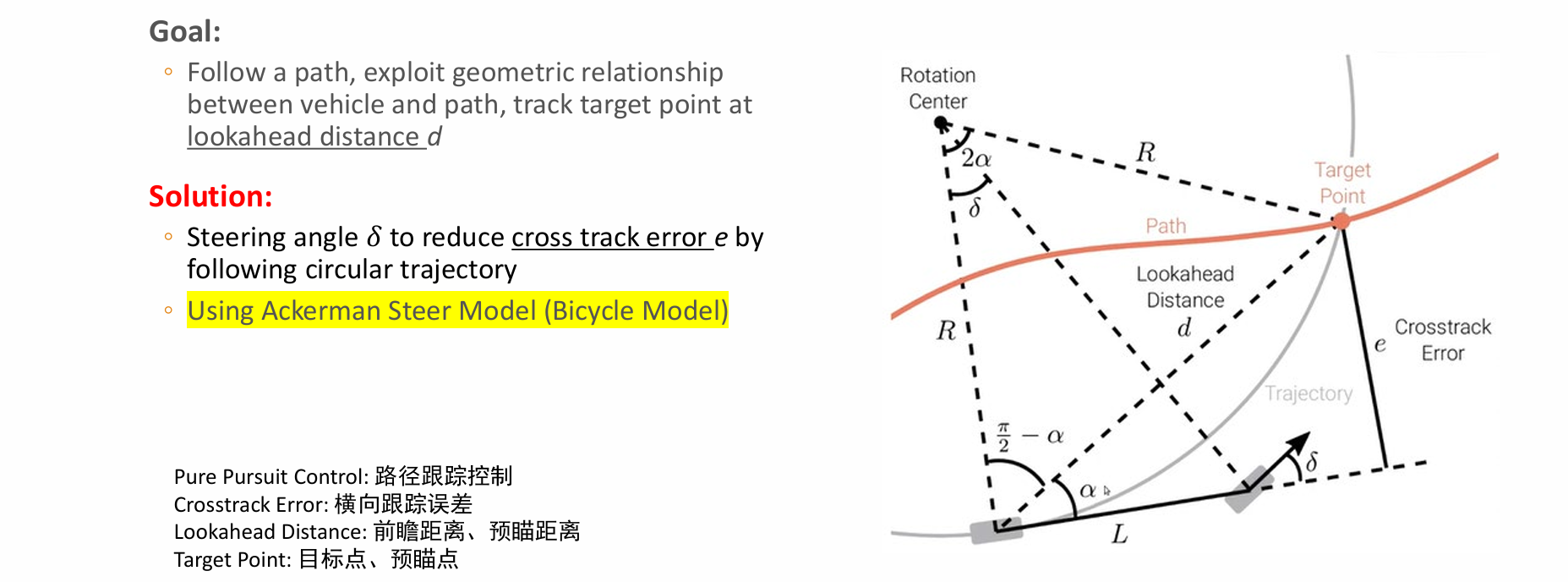
Pure Pursuit Control (cont.)
- 根据车速确定目标点后,转向角δ采用基于横向跟踪误差的比例控制器进行调节
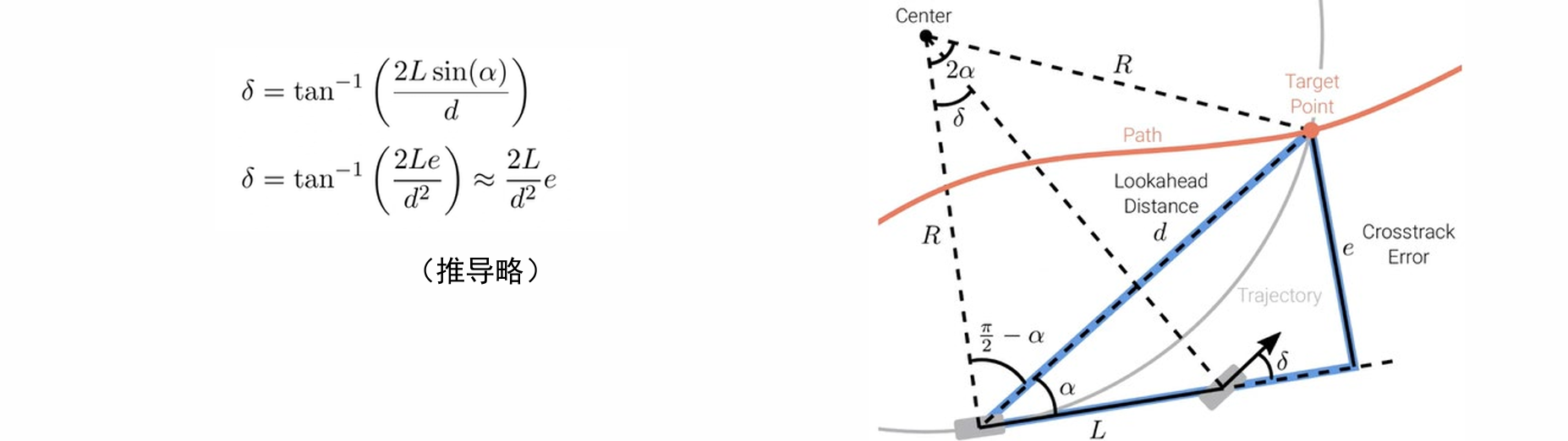
- 好处:系数常数可以通过模型计算
Stanley Control
- Stanly Control 属于几何控制,是 Pure Pursuit Control 的变种

优化控制 Optimal Control – MPC Control
- 前几种控制的问题:没有有效的前瞻性,缺乏长窗口的预见能力
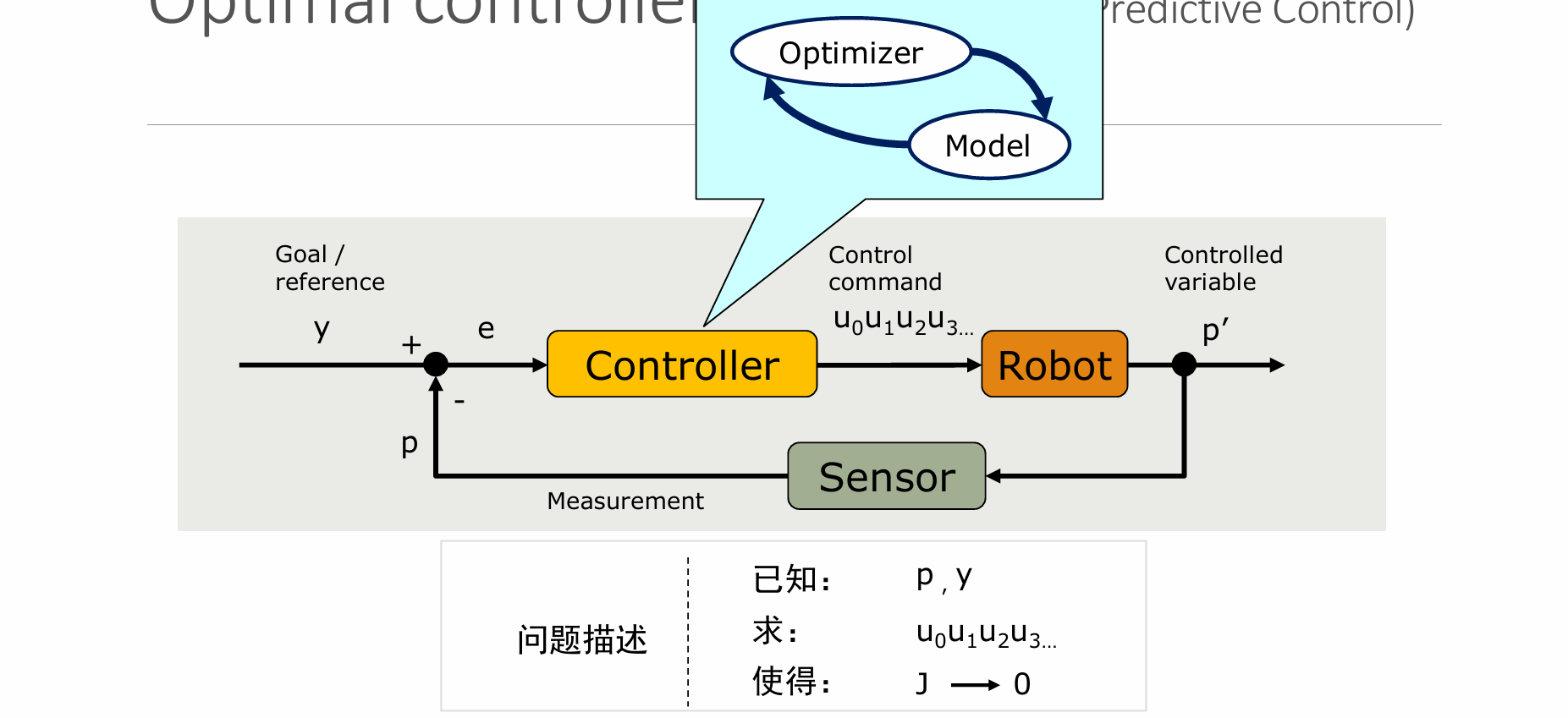
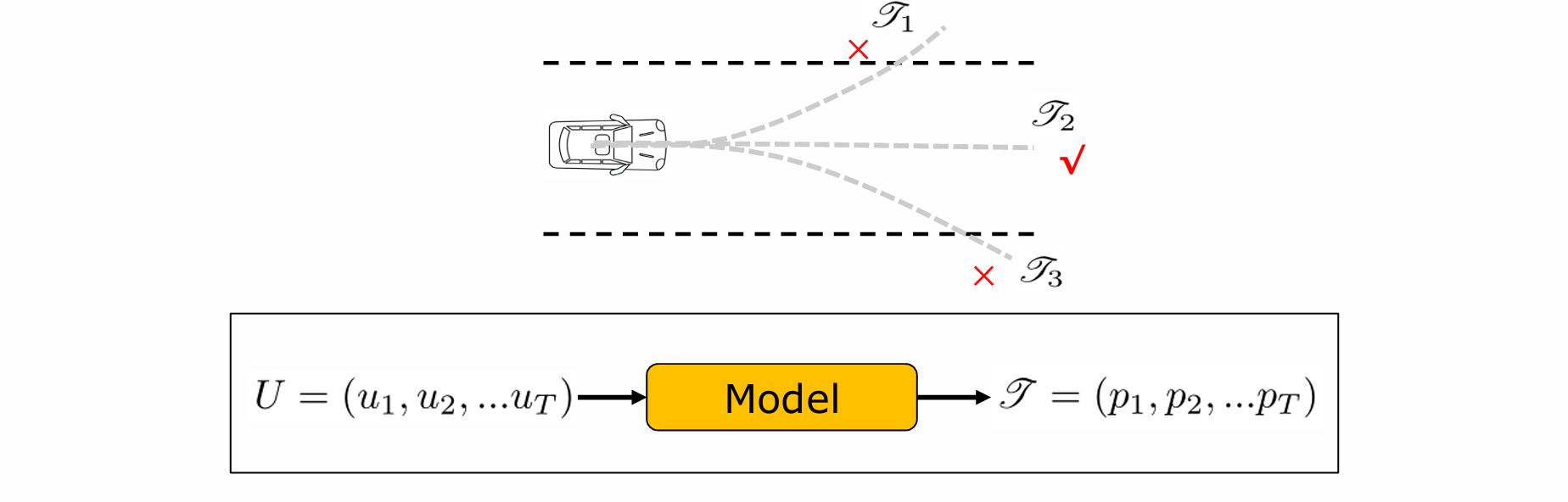
基于模型,将控制序列转换为轨迹序列,使得控制优化具有长时间窗口的预见能力
u1 -> p1;u2 -> p2;u3 -> p3,从而预测选择u2
- 优化的loss选择综合考量误差和控制幅度,对于每一组 u ,选择argmin
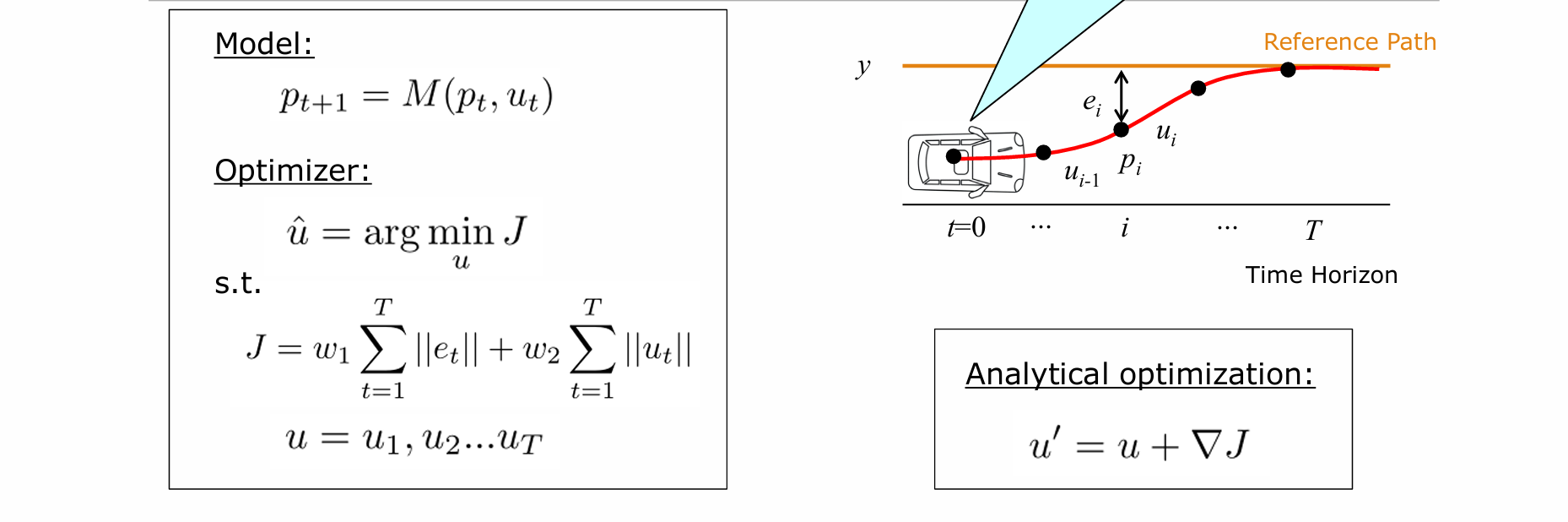
好处:将控制序列转换为轨迹序列,方法具有预测能力;坏处:依赖模型M的精度、优化时间代价高、简单模型会带来性能损失
控制算法的需求:
- 具有长时间窗口的预见能力
- 低时间代价
- 降低模型复杂度,提高模型精度
改进思路:
- 从Model的角度考虑
- 从Optimizer的角度考虑
- 从系统的角度考虑
基于学习的控制 Learning-based Control –End-to-end Control
MCP 方法的局限性:
- 基于精确模型的控制优化,时间代价高
- 控制精度依赖于模型精度
因而可以通过神经网络解决时间代价高的问题。深度模型可以描述复杂、高维、非线性过程

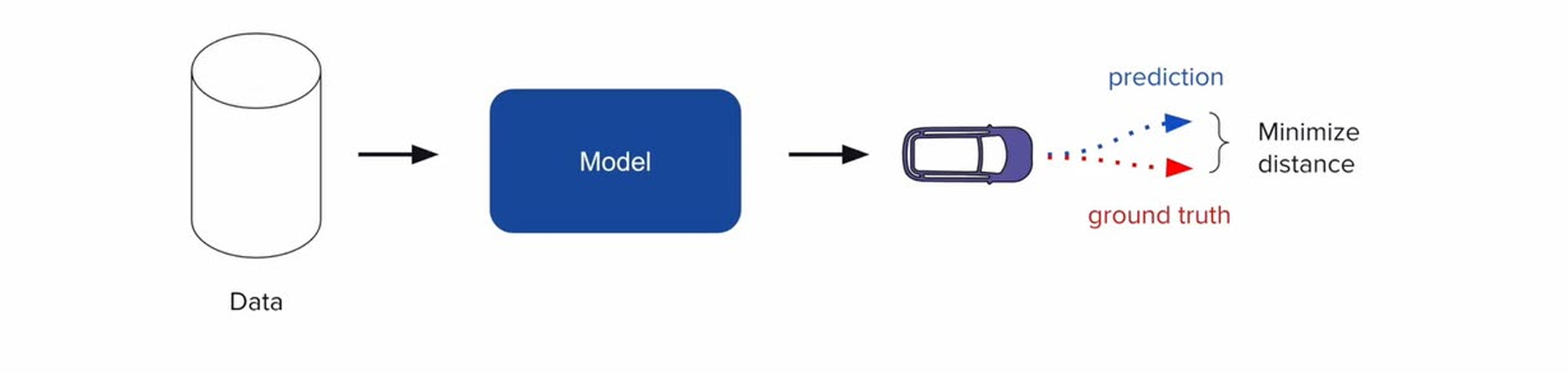
基于神经网络,实现从感知到控制的直接映射;依赖数据驱动,常采用强化学习或模仿学习
优点是整体性强,但可解释性较差
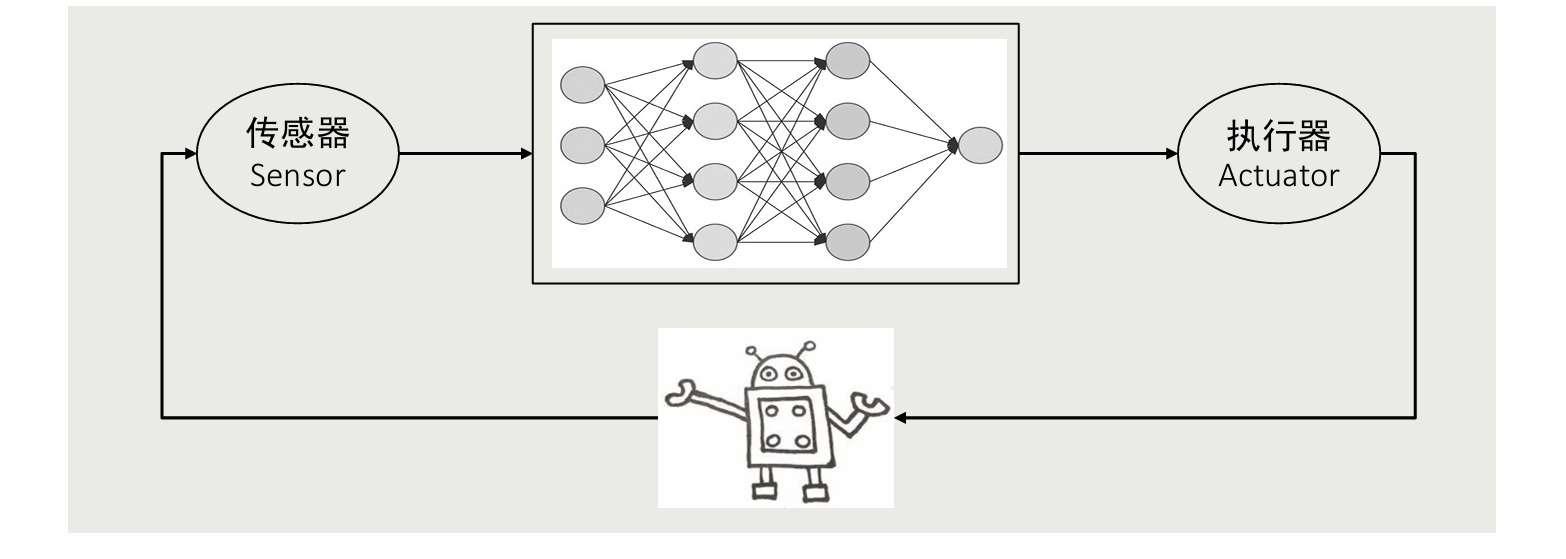
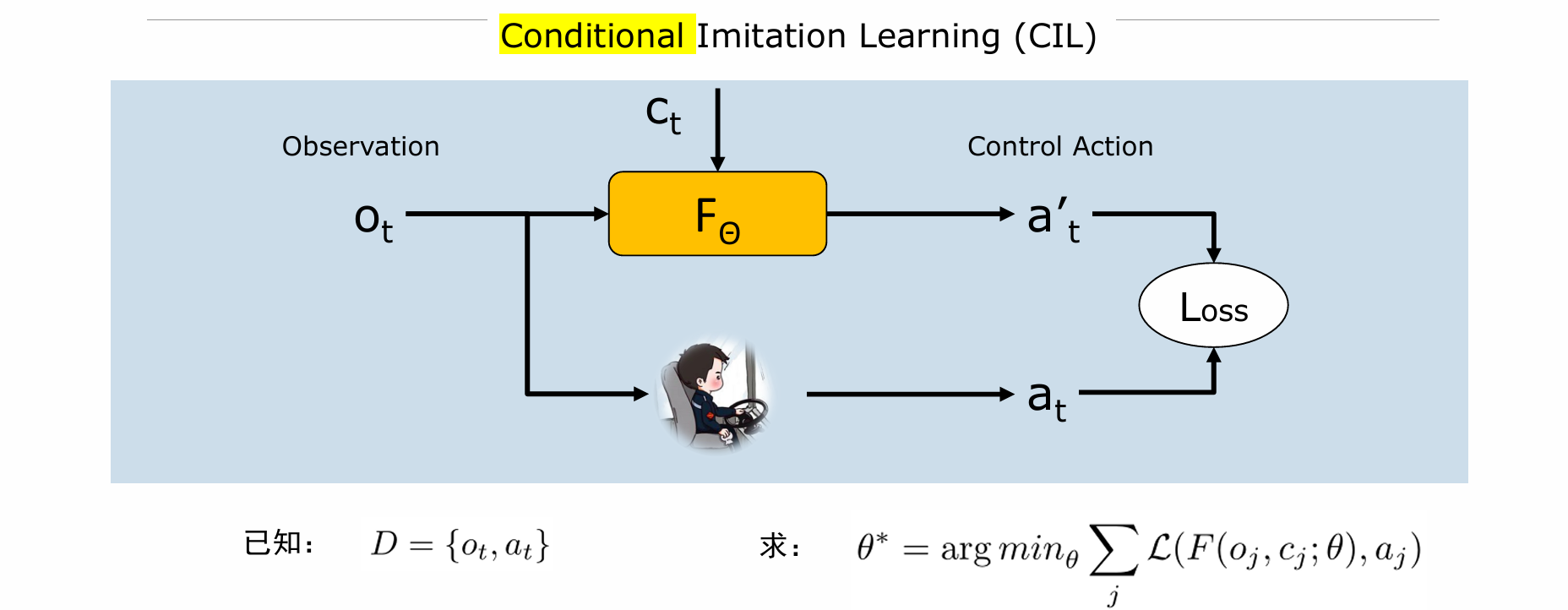
E2E Driving via Imitation Learning
- 学习模仿专家策略