数据结构与算法A 第四章字符串
字符串的基本概念
字符串是组成元素(结点)为单个字符(数字、文本字符或特定的符号)的线性表,简称“串”
字符串所包含的字符个数成为串的长度。空串:长度为零的串“”;空格串:“ ”
字符串的逻辑结构和线性表逻辑结构的区别:
- 字符串的数据对象约束为字符集
- 字符串的基本操作通常以“串的整体”为操作对象
字符串常数:用一对双撇号“xxxx”作为左右括号,中间字符个数有限
字符编码
字符类型是单字节(8 bits)类型
采用ASCII码对128个符号(字符集charset)进行编码
通用文字符号编码标准UNICODE
字符的编码顺序
字符编码表一般遵循“偏序编码规则”:根据字符的自然含义编码,使字符集中的编码顺序和其自然次序一致
字符偏序:根据字符的自然含义,某些字符间两两可以比较次序
encode()是符号的ASCII编码(序号)的映射函数
对于字母而言,大小次序就是按照字典编目次序。e.g. “monday”<”sunday”<”tuesday”.”123”<”1234”<”23”
字符串ADT
子串:s1 = a0a1a2…an-1和s2 = b0b1b2…bm-1,(0 ≤ m ≤ n)若存在整数i (0 ≤ i ≤n-m),使得bj = ai+j, j = 0,1,…,m-1同时成立,则称串s2是串s1的子串,或称s1包含串s2
真子串:子串非空且不是自身
1 | class string |
字符串的存储结构和实现
字符串的顺序存储
顺序存储:C++标准字符串。采用char S[M]的形式定义字符串变量,M是常量保持不变
串的结束标记:’\0’,长度为M的字符串实际最大容量的为(M-1)
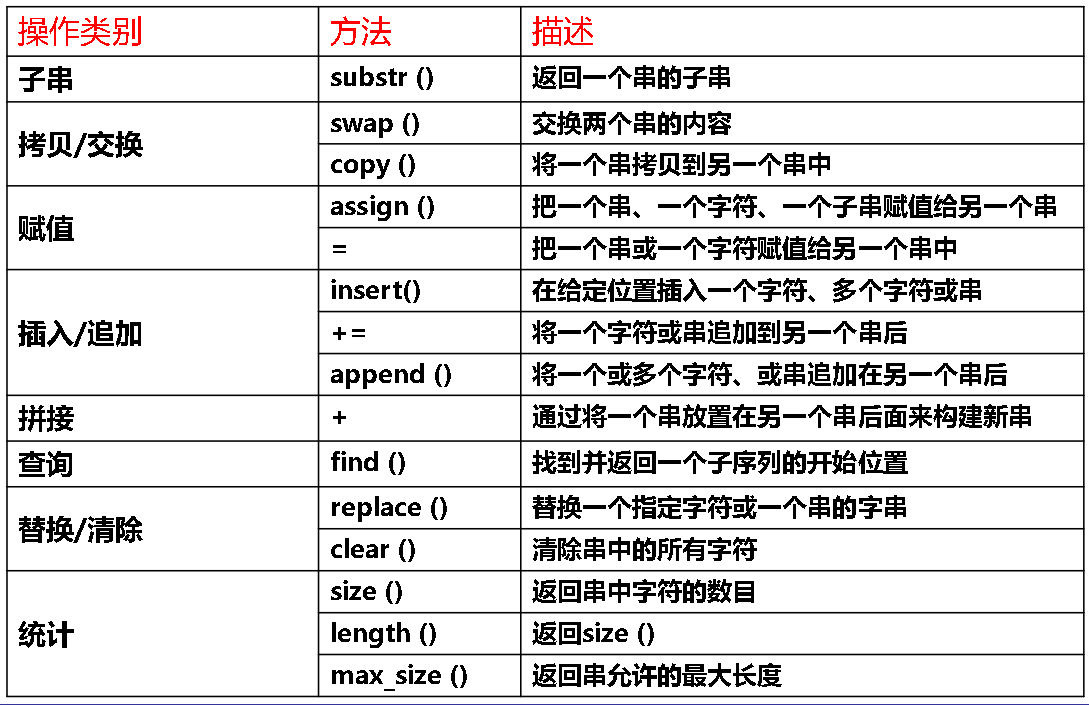
标准字符串函数
- 串长函数:返回字符串的长度。int strlen(char *s);
- 串复制:将s2值复制给s1,返回指针指向s1。char *strcpy(char *s1, char *s2);
- 串拼接:将串s2拼接到s1的尾部。char *strcat(char *s1, char *s2);
- 串比较:int strcmp(char *s1, char *s2);(= ,>,<)
- (左)定位函数:c在s中第一次出现的位置。char *strchr(char *s, char c);
- 右定位函数:c在s中最后一次出现的位置。char *strrchr(char *s, char c);
字符串类class String的存储结构
字符串的长度动态变化,不适合采用动态链表形式
不再以字符数组char S[M]的形式出现,而采用一种动态变长的存储结构
String类部分算子列表
- s2的长度>s1,将s2赋值给s1时,必须释放s1原有空间delete[] s1.str,然后在动态存储区开辟新的存储数组,再把s2的内容复制到新数组中
字符串运算的实现
C++标准串运算的实现
- 字符串的比较strcmp
1 | int strcmp(char *d,char *s) |
- 正向寻找字符
1 | char *strchr(char *d,char ch) //查找ch在d中第一次出现的位置 |
- 反向寻找字符
1 | char *strrchr(char *d,char ch) |
String串运算的实现
- String串运算的实现
1 | String::String(char *s) |
- 拼接算子
1 | String String::operator+(String& s) |
- 赋值算子
1 | String String::operator=(String& s) |
- 抽取子串函数
1 | String String::Substr(int index,int count) |
4.3 字符串的模式匹配
字符串的模式匹配:在文本(T)中寻找一个给定的模式(P)
任务:用给定的模板P,在目标字符串T中搜索与模板P全相同的一个子串,并返回P 和T匹配的第一个子串的首字符位置
模式匹配的分类:
- 精确匹配:如果在目标T中至少一处存在模式P,则称为匹配成功,否则失败
- 模式中的?为通配符
- 近似匹配:如果模式P与目标T(或其子串)存在某种程度相似,则认为匹配成功
- 常用衡量字符串相似度的方法是根据一个串转换成另一个串所需的基本操作数目来确定。(编辑距离 Edit Distance)
- 基本操作由字符串的插入、删除和替换三种操作来组成
朴素的模式匹配算法
从主串T的第一个字符起和模式串P的第一个字符进行比较。若相等,则继续比较T和P的后续字符,否则,从主串S的第“2”个字符起再重新和模式P的第“1”个字符进行比较
最佳情况:在目标的前M个位置上找到模式,时间复杂度O(M)
最差情况:模式与目标的每一个长度为M的子串进行比较。目标形如an, 模式形如am-1b。总比较次数:M(N-M+1)。时间复杂度:O(M*N)
1 |
|
字符串的特征向量KMP算法
P中每个字符对应一个移位值k,该值仅依赖于模式P本身,与目标T无关
当某次比较出现Pi != Tj时,意味着满足:P(0…i-1)=T(j-i…j-1)成立
- 如果P(0…i-2) = P(1…i-1)成立,即模式后移一位后P(0…i-2)=T(j-i+1…j-1)。
- 如果不满足可依据需查找P(0…i-3)与P(2…i-1)是否相等
- 以此类推必然可以找到某个值k使得P(0…i-k-1) = P(k…i-1)成立,此时把模式右移k位开始下一次匹配
P的前缀子串(“首串”):P的前K个字符组成的子串P(0…k-1)。i位置的后缀子串(“尾串”):P在i之前的k个字符组成的子串P(i-k…i-1)
对于Pi而言,一旦与目标Tj失配时,模式的下标从位置i移动到位置k,Pk直接与Tj比较,而跳过了P(0…k-1)。如果把目标Tj看做是不动的,则模式向右滑动了i-k位
把对应模式中每个字符Pi的这个k值称其为特征数ni,即P(0…i-1)中最大相同前缀子串和后缀子串。所有特征数组成了模式的一个特征向量,next数组。
特征向量 N 用来表示模板 P 的字符分布特征,简称 N 向量和 P 同长,由m个特征数n0 …nm-1非负整数组成,记为N = n0n1n2n3……nm-1。k就是要求的特征数ni
特征数ni (-1 ≤ ni ≤ i )是递归定义的,定义如下:
- n0 ←-1,对于i > 0的ni ,假定已知前一位置的特征数 ni-1 ,并且ni-1 = k ;
- 如果pi = pk ,则ni ← k+1 ;
- 当pi ≠ pk 且 k ≠ 0时,则 令k ← nk ; 循环直到条件不满足;
- 当pi ≠ pk 且 k = 0时,则 ni = 0;
个人理解求next数组方法:
- 第零和一位:next[0] = -1 ;next[1] = 0
- 非第零和一位:看第0位开始的k个数和从前一位往回数k个数是否相同。找出最大的k
- 如果找不到,k = 0
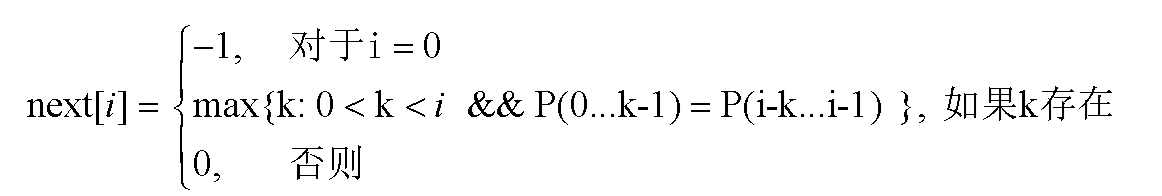
1 | int* findNext (string P) |
- 求出的next数组还可以进一步优化。若求出next[i]=k,当匹配时发现Pi!=Tj时,按照特征向量的意义,该把模式右移i-k位,用Pk与Tj比较。如果Pi!=Pk,则Tj!=Pk,还需再右移,用Pnext[k]来与Tj比较
1 | int* findNext(string P) |
KMP模式匹配算法
- KMP的算法的时间复杂性为O(N)。求next数组的时间为O(m)。因此,KMP算法的时间为O(n+m)。
1 | int KMPStrMatching (const String & T,const String & P,int * N) |

第四章 字符串 OJ作业
1:全在其中
1 | /*描述 |
2:字符串乘方
1 | /*描述 |
3:合格的字符串
1 | /*描述 |


