自然语言处理 lec7 phrase

Syntactic Analysis I

Syntactic Structures

• 讨论了词义消歧、语言模型序列(这句话好不好)、序列标注(词性是否符合语法习惯)

• 我们没有触及另一个有趣而复杂的话题：语法

Syntax

• 语言遵循一定的语法规则(隐性的)，而且会不断变化：

  1. 可以编译的有一定规则和形式
  2. 没有歧义，他人能懂

• 同时附带语义

• 超越字级分析或纯序列分析

• 分析语法的一种可能解决方案是将句子映射到复杂的结构中(句法分析)，例如树或图形。希望讨论的不再是序列而是更复杂的结构——树或图…

• 所需：设计计算解决方案来恢复这些具有挑战性的句法结构

  1. 来自语言学的一个很好的理论，希望能完美地描述所有的语言现象
  2. 一种将句子映射到某些目标结构的算法
     1. 目标结构的形式可以多种多样，例如序列、树、图形等
     2. 目标结构的形式可以多种多样，例如序列、树、图形等
  3. 需要一个方法来评价好坏

Theories

• 句法结构(语法)：管理单词序列的语法或格式正确的规则，通常与某种语言有关

• 语义：单词、短语、句子或段落的含义是如何构建的，如何基于世界或世界的近似值(意思如何聚合)

• 语用(上下文相关)：语境如何影响意义，例如，语言在社交互动中如何被解释

Constituent

Noun Phrases

• 围绕至少一个名词的单词序列

• 功能为名词 e.g. the reason he comes into the Hot Box

• 具有相似的存在模式，经常出现在动词之前(功能相同)，上下文类似

• Constituents(成分)：单词组可以表现为整体，表现为具有某种模式

  1. 在句子中作为整体移动
  2. 可以与一些其他成分合并

• 重点：如何找到成分并恢复成分之间的关系

Constituency Parsing

• 基本思想：短语结构将单词组织成嵌套的成分，将短语结构表示为树

• 希望得到如下输出：

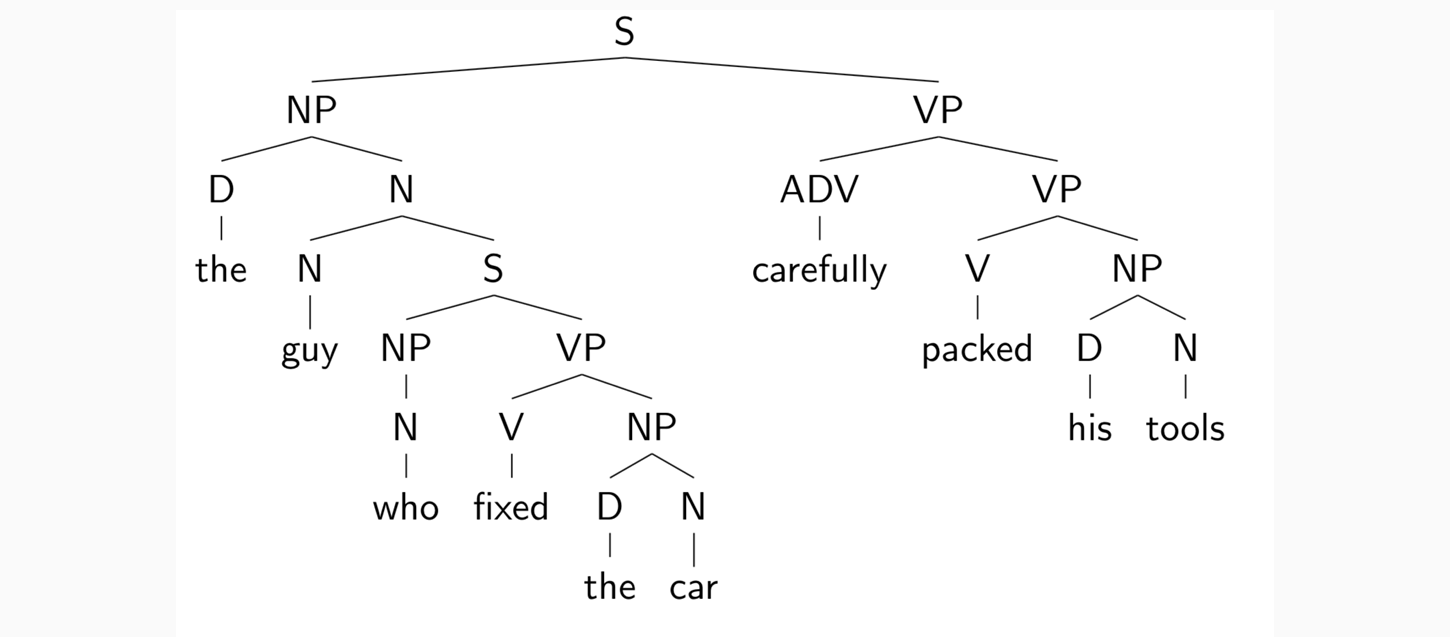
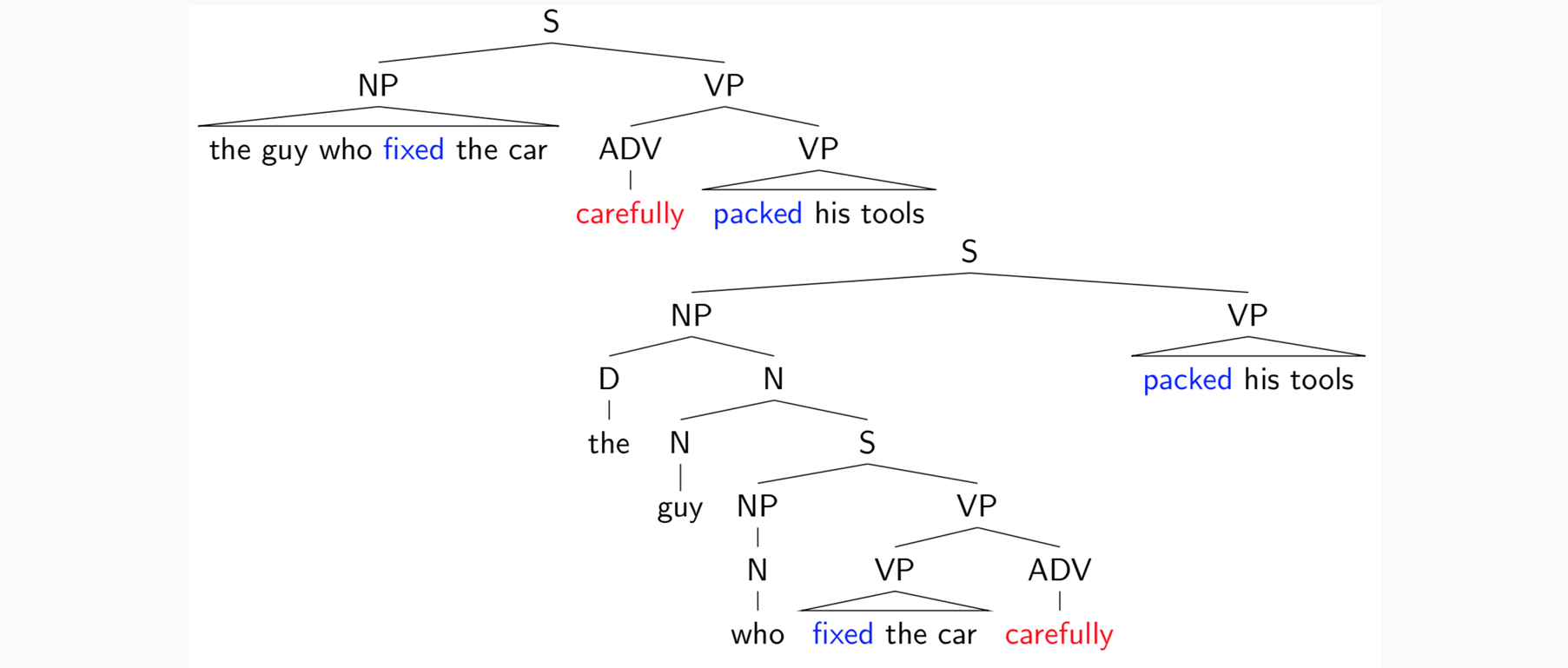
Applications of Parsing

• 可以帮助语法改错

• 特定领域下的机器翻译

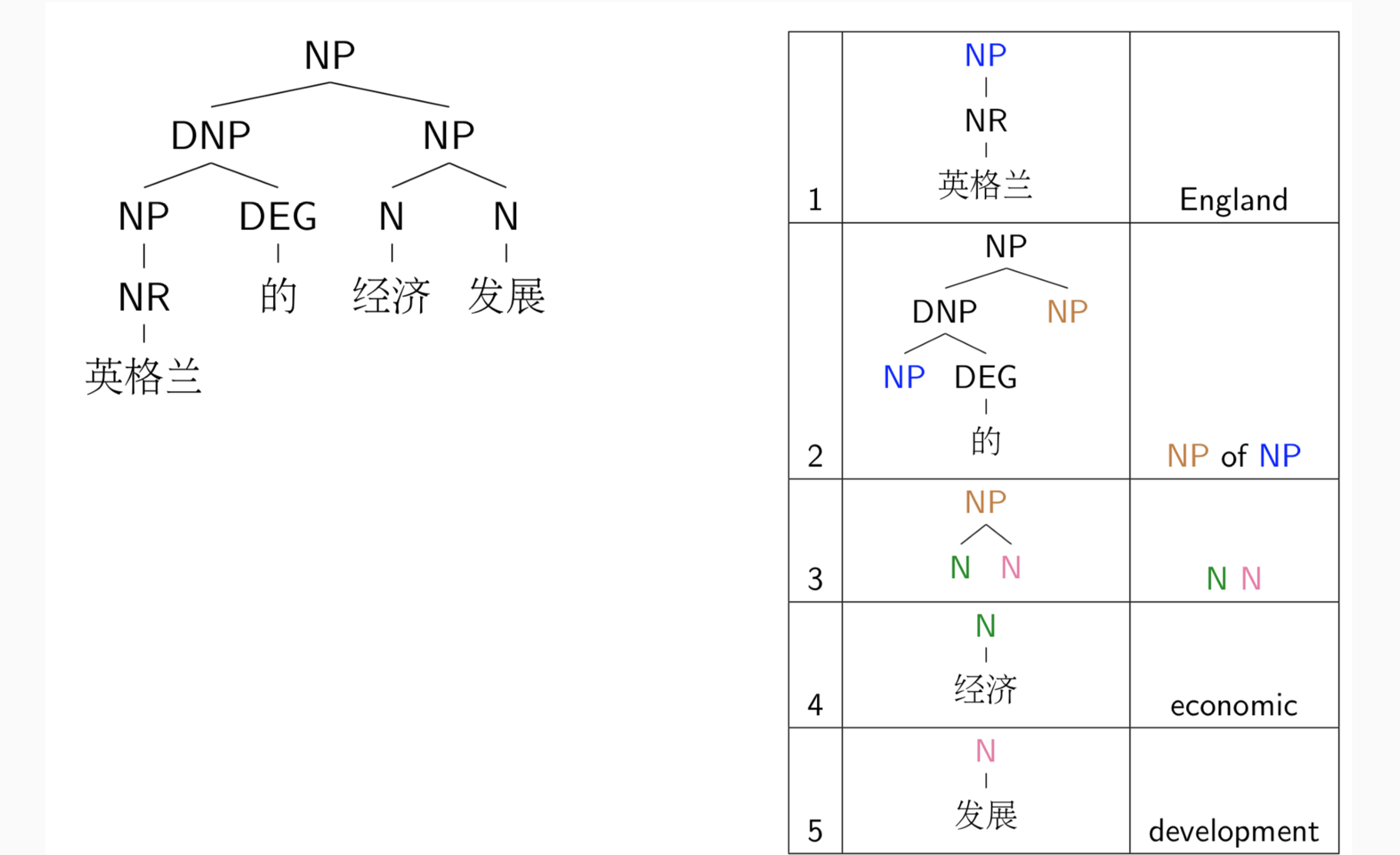
• 应用规则进行翻译：

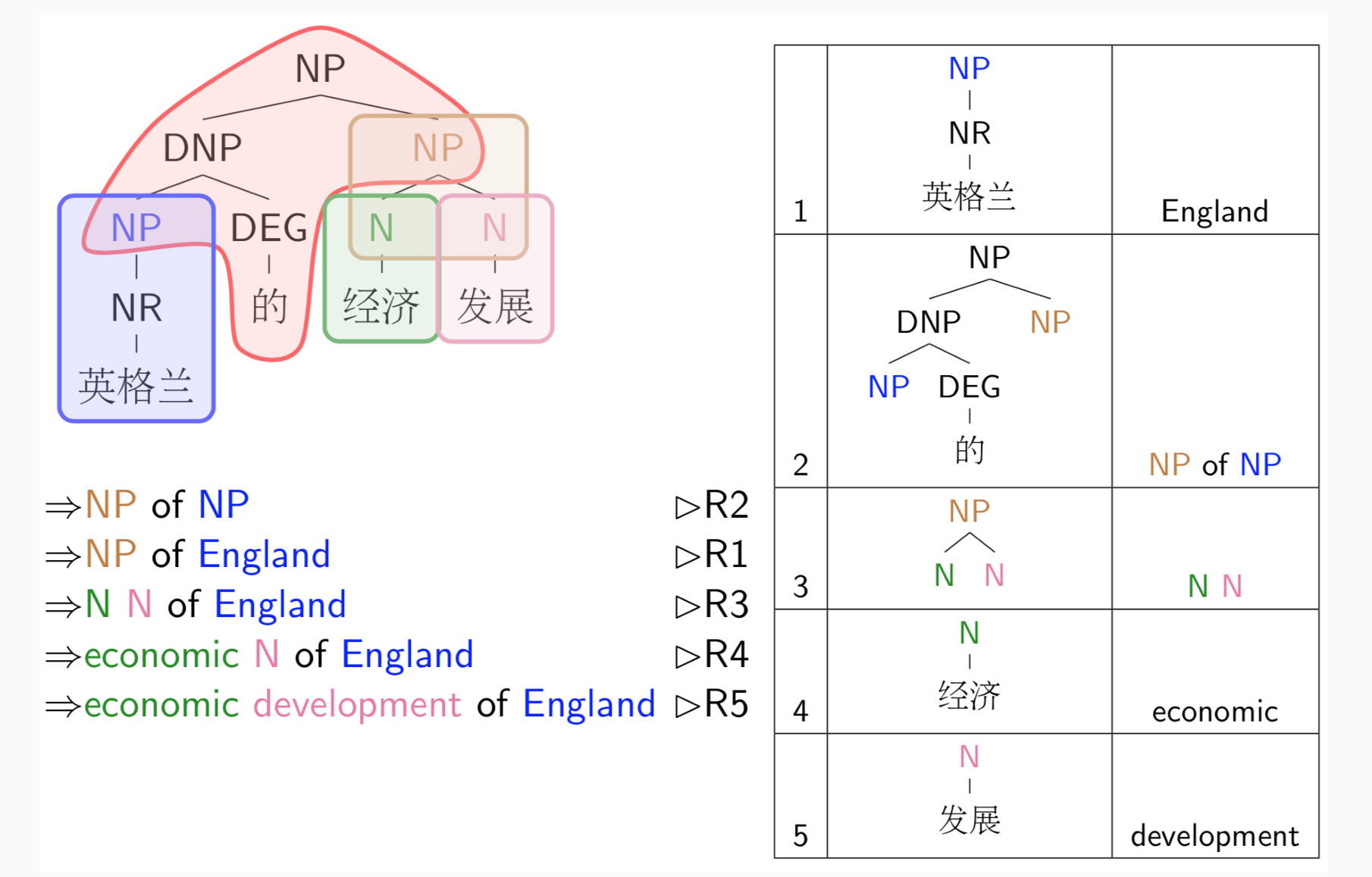
• 此类型的机器翻译应用于必须有出处一一对应的机器翻译，例如特定领域的操作说明

Linguistic Structure Predictions

• word -> word sequence -> tree of words -> graph of words

• trees, graphs, … :需要多次决策构成复杂结构，需要多个分类器。需要考量：

  1. 搜索空间——CFG
  2. 如何考量好坏——PCFG
  3. Decode：找到获得最高分的分析
  4. 参数估计：找到好的参数
     

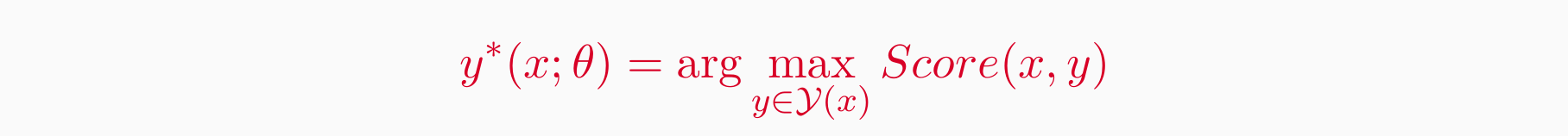
Grammars and Parsing

Formal Languages

• 形式语言：字母表上的词串集，从字母表中生成长度为n的词串构成集合Σ。Σ∗ 表示 Σ 上有限长度的所有字符串的集合。给定一个字母表 Σ，Σ∗ 的任何子集都是字母表 Σ 上的形式语言

• Language models：使用有限规则定义字符串 S ∈ Σ* 的特定子集

• 形式语法：可以生成自然语言的所有且仅可接受句子的语法

• 语法 G 由以下部分组成：

  1. 有限集 Σ terminal symbols(日常生活中能够观察到的词)
  2. 有限集 Σ 以外的 nonterminal symbols(日常生活中不可见的词)，记为N
  3. 一个可识别的nonterminal symbol，START 符号 S
  4. 生成规则的有限集 R，每个规则的形式：
     

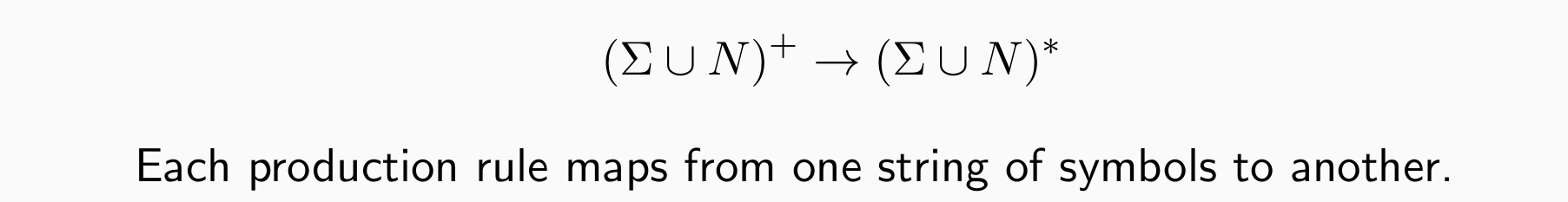
• 语法可用于生成一组字符串

• 语法可用于将字符串映射到符号结构

Context-Free Grammars(上下文无关文法)

• A context-free grammar consists of:

  1. Σ of terminal symbols, e.g., words, characters, …
  2. N of nonterminal symbols，与Σ不交
  3. 生成规则的有限集 R，每个规则的形式：
     

• 将规则集极大的缩小，只有nonterminal可以转化成串，nonterminal转换时与周围无关

• 生成仍然不可控，因为右边的长度是不可控的，因而需要约束后者

• 问题：能生成符合语法的句子，但是语义可能奇怪。判断语法时与词义无关

Grammar Equivalence(语法等价性)

• Equivalence:两组不同的语法生成相同的词串集合

• Strong Equivalence:生成相同的字符串集并为每个句子分配相同的短语结构，生成的树形结构完全一样

• Weak Equivalence:生成相同的字符串集，但不为每个句子分配相同的短语结构

Chomsky Normal Form

• 乔姆斯基范式中的上下文无关语法 G = （N，Σ，R，S） 如下：

  1. N is a set of non-terminal symbols; Σ is a set of terminal symbols
  2. R 是一组规则，采用以下两种形式之一：
     1. X → Y ZforX ∈N, and Y,Z ∈N，一个nonterminal变成两个nonterminal
     2. X → xfor X ∈N, and x∈Σ，一个nonterminal变成一个terminal

• 定理：每个 CFG 都可以转换为乔姆斯基范式的等效 CFG

Probabilistic Context-Free Grammars

• 一个句子什么是语法？如何得到句子的短语结构吗？

• 概率型的上下文无关文法：给每个规则赋分(概率)，如果能从规则得到演算，则可以直接将规则分数相乘得到最终分数：规则的得分怎么来？反映什么？

• 规则 A1 → β1，A2 → β2 的树 t 的概率,…是：其中 q（Ai → βi） 是规则 Ai → βi 的概率。找出一句话生成所需要的规则，得分为规则的乘积

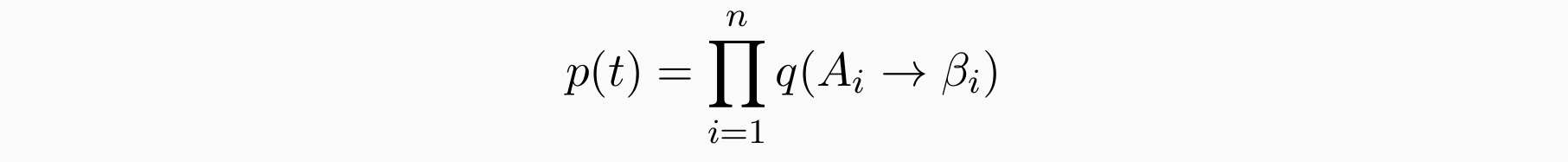
• 当我们扩展 Ai 时，我们选择 Ai → βi 的可能性有多大？对于每个nonterminal Ai:

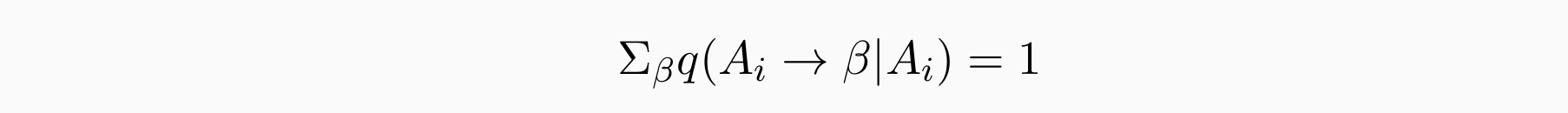
• PCFG 生成 CFG 的随机派生

• 每个事件（按生产规则扩展非终端）在统计上独立于所有其他事件

• PCFG的问题：

  1. PCFG是有偏估计
  2. PCFG有很多0，规则集合不完备
  3. 对结构认定存在差异，有前后矛盾

• PCFG的性质：
  1. 概率型的
  2. 假设我们有一个句子 s，该句子的派生集是 T （s），由 CFG 定义。然后 PCFG 为 T （s） 的每个成员分配一个概率 p（t）
  3. Score 函数 （probability） 可以对树进行排名，句子 s 最可能的解析树是：
     

Deriving a PCFG from a Treebank

• 给定一组示例树（树库），底层 CFG 可以简单地是语料库中看到的所有规则 -> 最大似然估计用于对 CFG 中的每个规则进行加权。其中，计数取自示例树的训练集

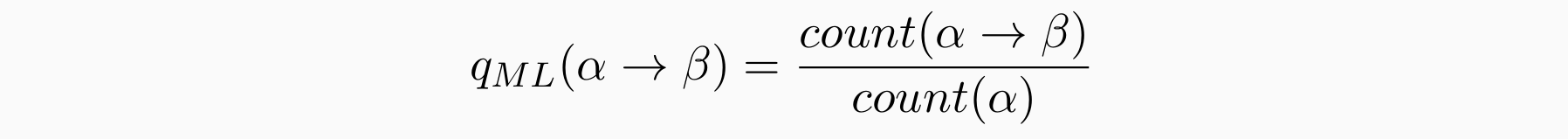
• 如果训练数据是由 PCFG 生成的，那么随着训练数据大小趋于无穷大，最大似然 PCFG 将收敛到与真实 PCFG 相同的分布

Parsing with a PCFG

• 给定PCFG和给定一句话s，希望得到T（s）为产量为 s 的树集

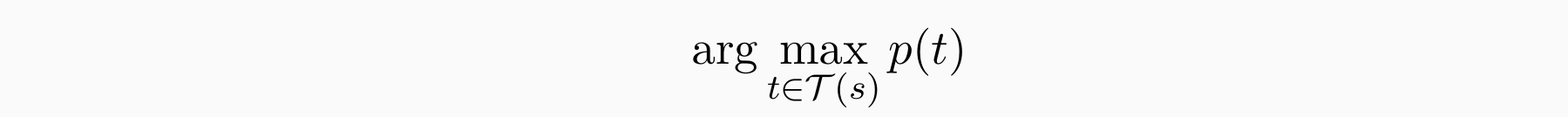
• 解决方法：分治递归，the Cocke-Kasami-Younger (CKY) algorithm

The CKY Algorithm

• 动态规划表π[i，j，X]：nonterminal X 跨越 i 和 j 之间的单词的最大概率

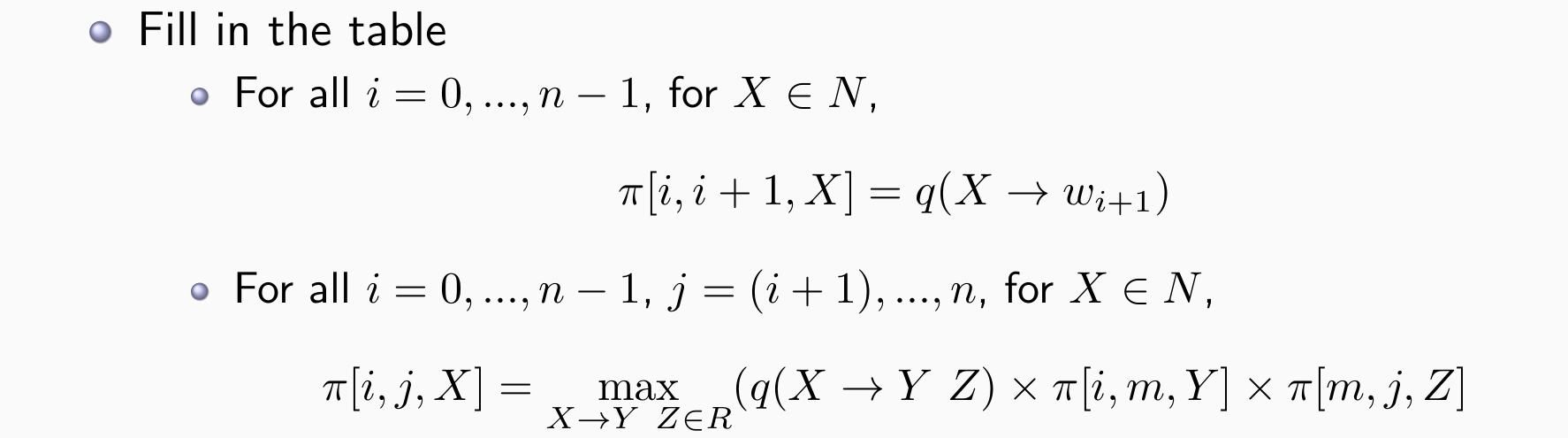
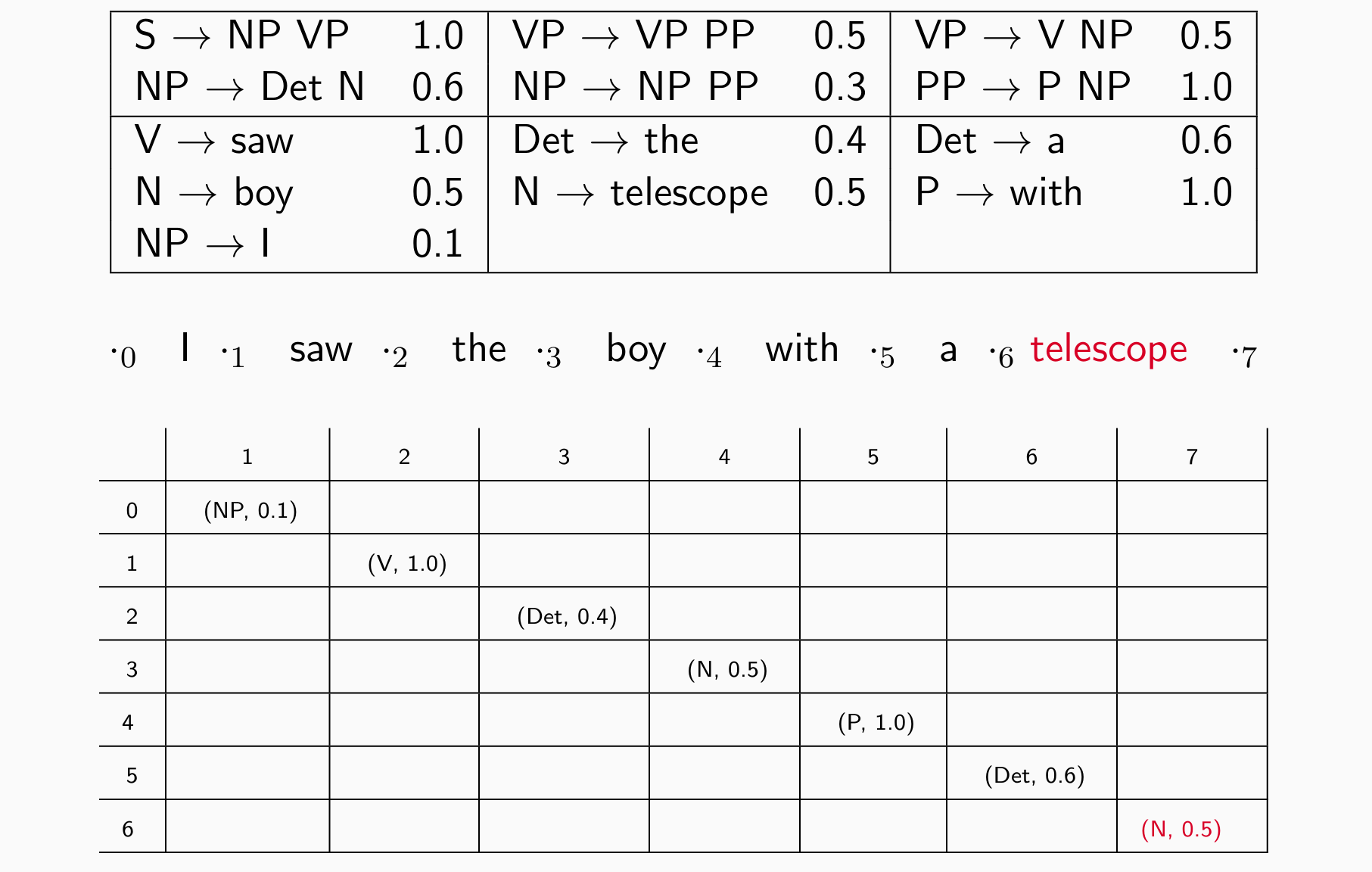
• 一个词看完后看两个词 e.g. I saw的分数

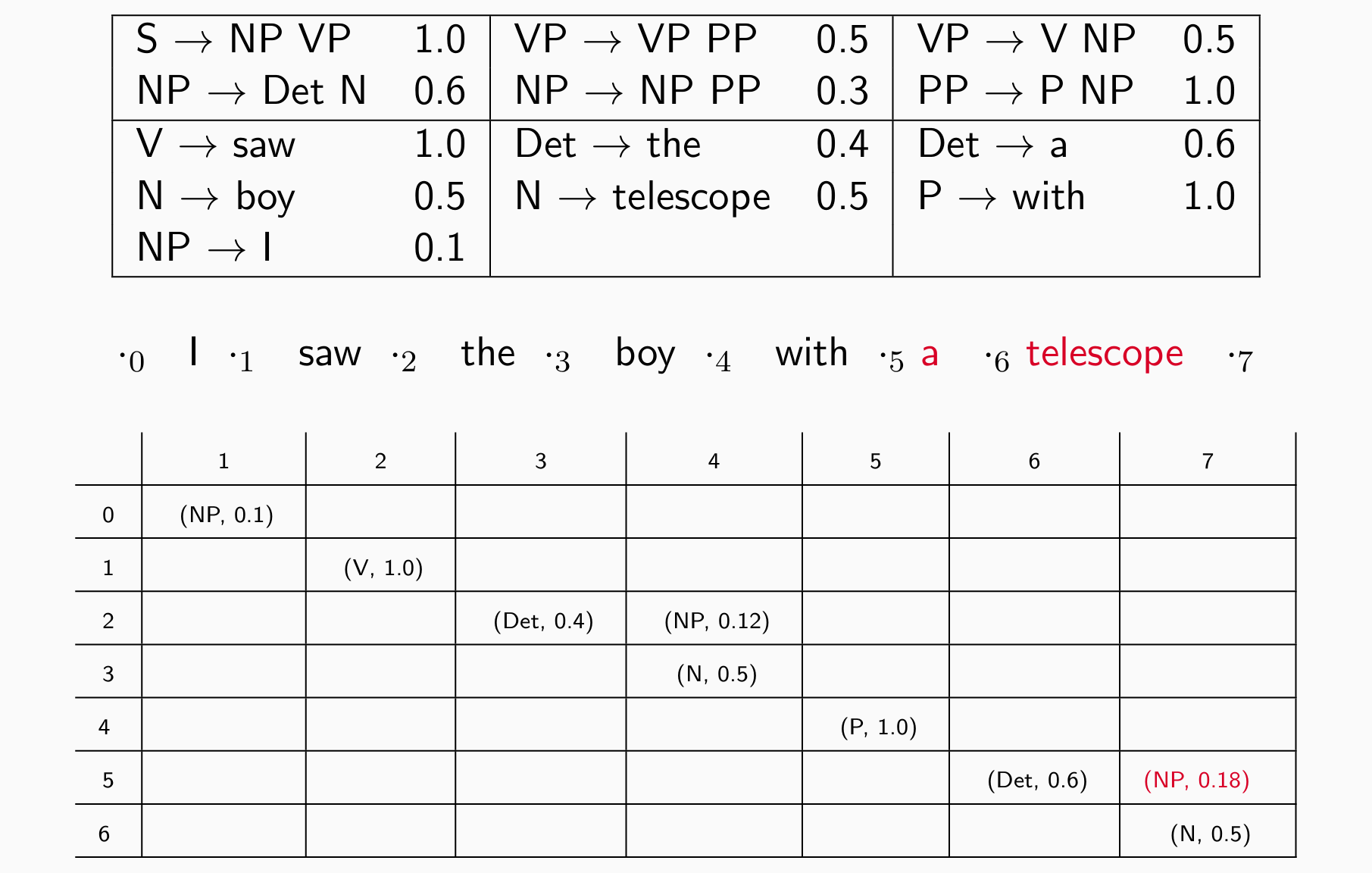
• 再看三个词 e.g. saw the boy

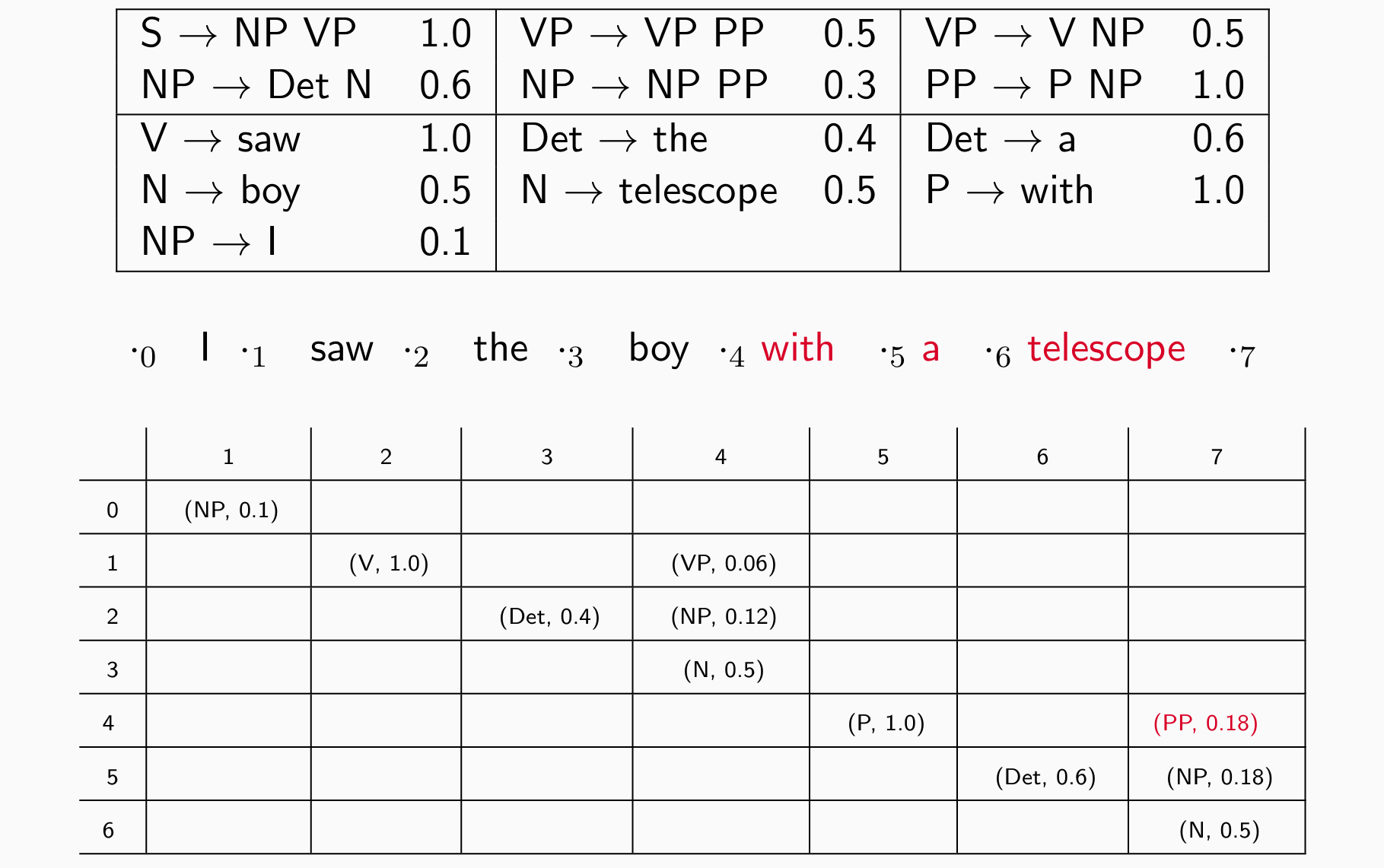
• 再看四个词 e.g. I saw the boy

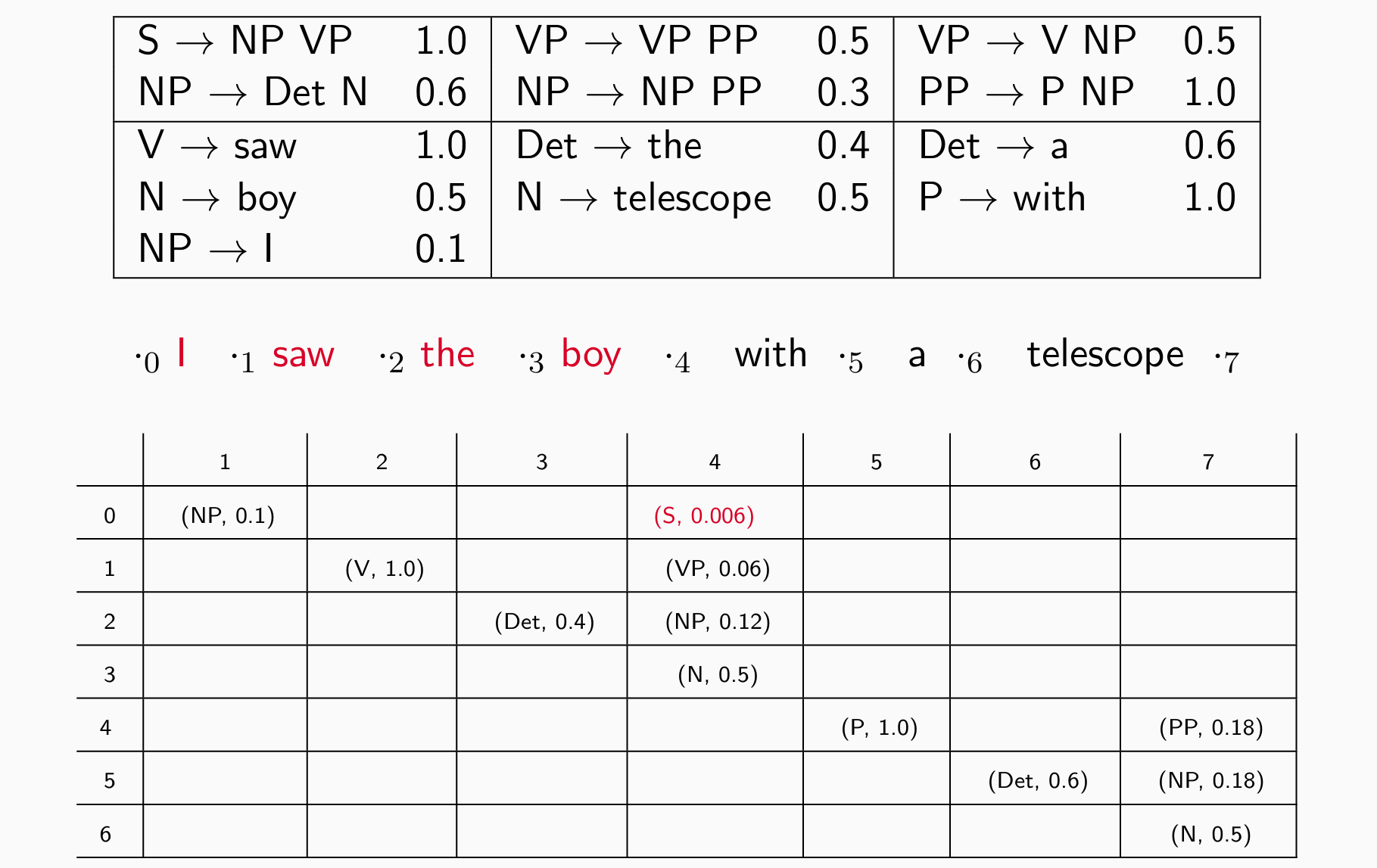
• 直到S出现在右上角：

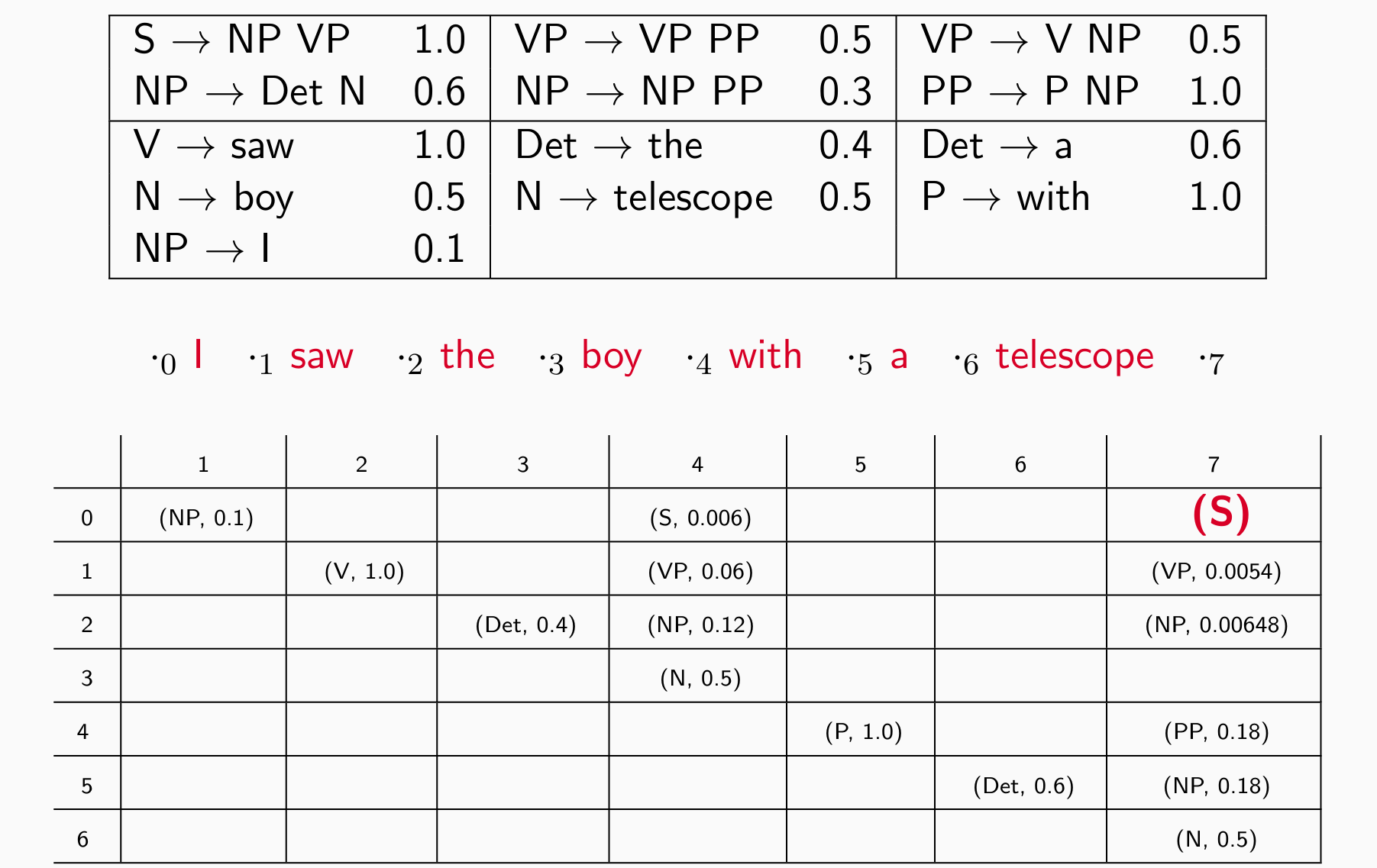
• 可以转成log做加法

• 可能有多个规则达成最终状态，存储多种可能性和得分取最佳

• 简单一点的任务——识别：确定 CFG 是否可以解析句子用PCFG生成

Evaluation

• Labeled Precision, Labeled Recall, F1：比较边和金标准的边是否一致，考察规则是否正确

• 传统方法：

  1. Train PCFG with MLE on the Penn Treebank
  2. Compute parse trees for PTB 23 using your models, e.g., your CKY
  3. Trick against data sparseness in lexicon: delete words, train and test on sequences of POS tags
  4. This yields labeled F-score in the low 70’s

• 问题：

  1. 对词级别的信息缺乏敏感性
  2. 对结构频率缺乏敏感性

Summary

---