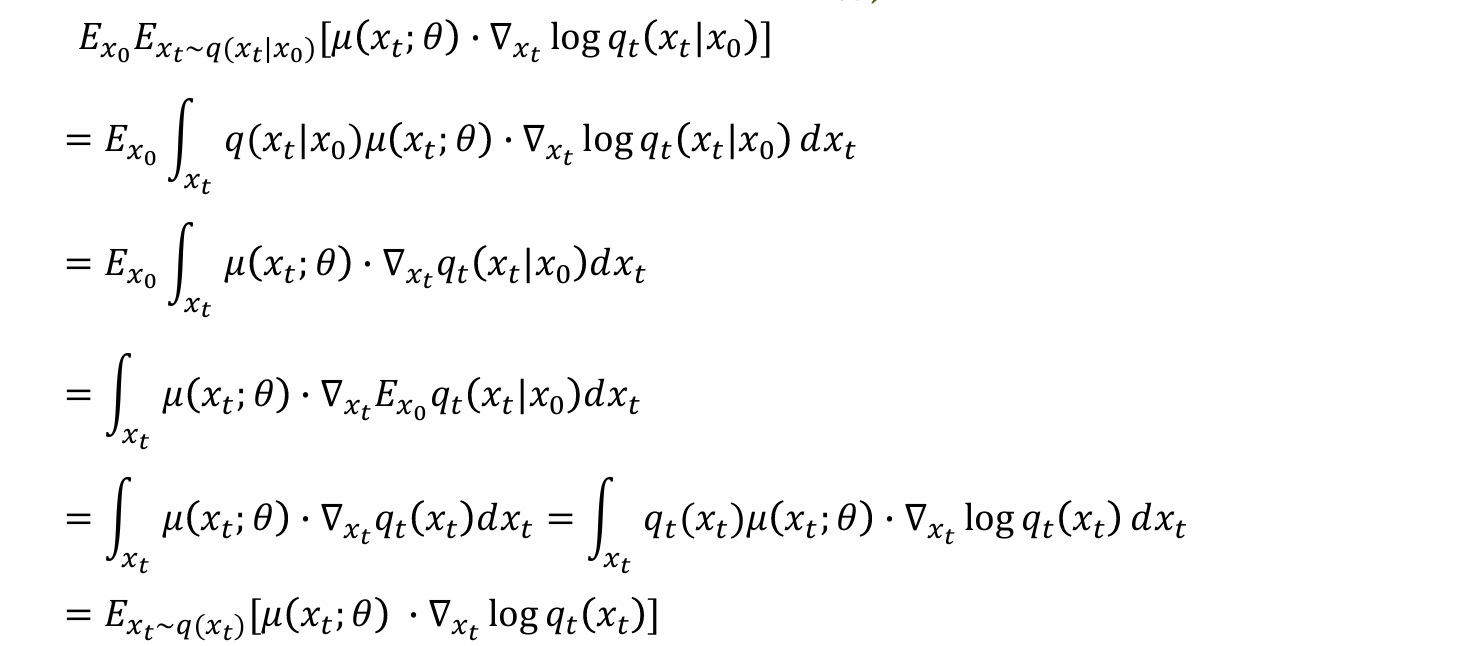生成模型基础 08 Diffusion Model
Difussion Model
Why we introduce diffusion in generative modeling
x为复杂分布无法表达,但是可以通过“扩散”,形成可以建模的简单分布z~N(0, I)
核心思路:如果能够逆转这一过程,则可以重新得到x,完成生成模型的目标
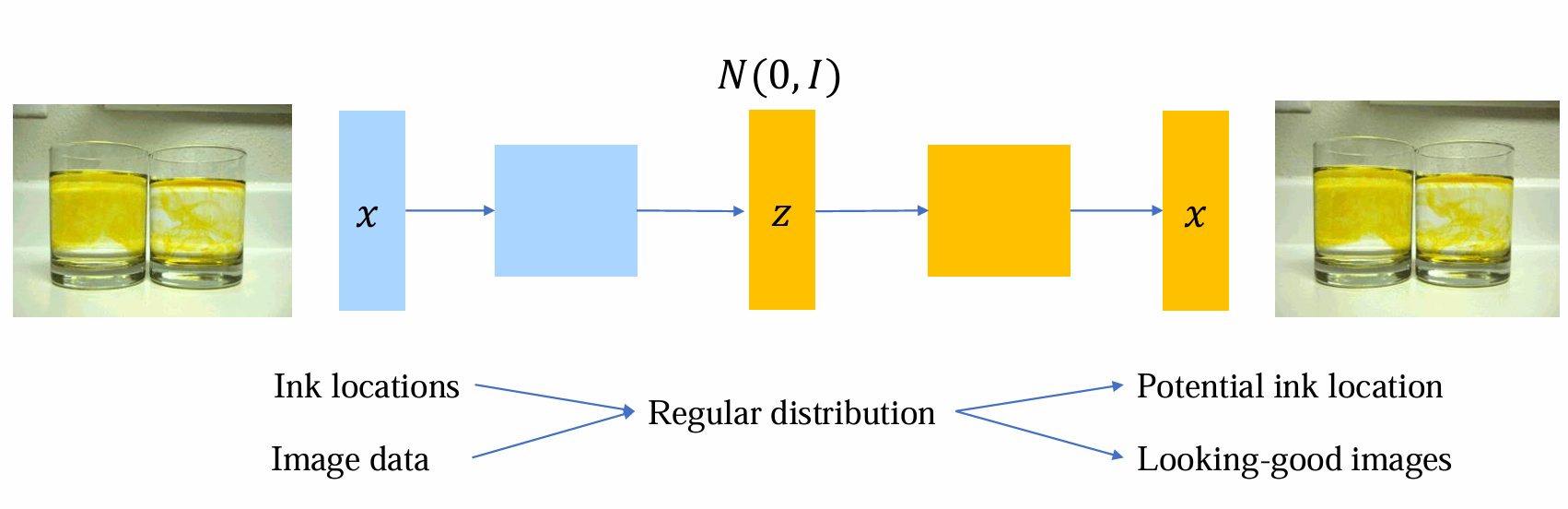
- 问题:
- 高维image如何变成噪声
- 如何逆转这一过程z -> x
- 如何训练模型
Forward process

forward pass:image -> noise
标记法:
- image -> x0
- image(data)服从的分布:q(x0)
- 随机变量x服从高斯分布:N(𝑥; 𝜇, 𝜎²𝐼)
- 从高斯分布中采样:𝑥 = 𝜇 + 𝜖𝜎
前传的过程不断加噪,一共加T次,每次加一点

- 可以从中sample中x1:
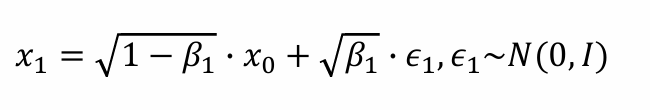
式子的前项可以理解为减弱x0中原来含有的信息,而后一项可以认为加入噪声信息𝜖1
后续的加噪过程与q(x1|x0),相似,可以依次计算q(x2|x1),采样出x2,……

- 从而可得递推公式:
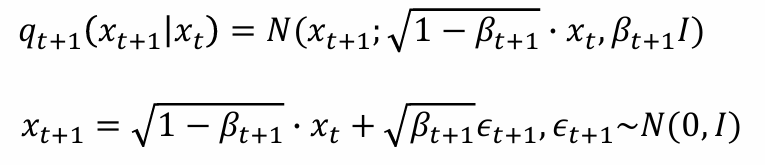
- 计算和上上时间步的关系可得:
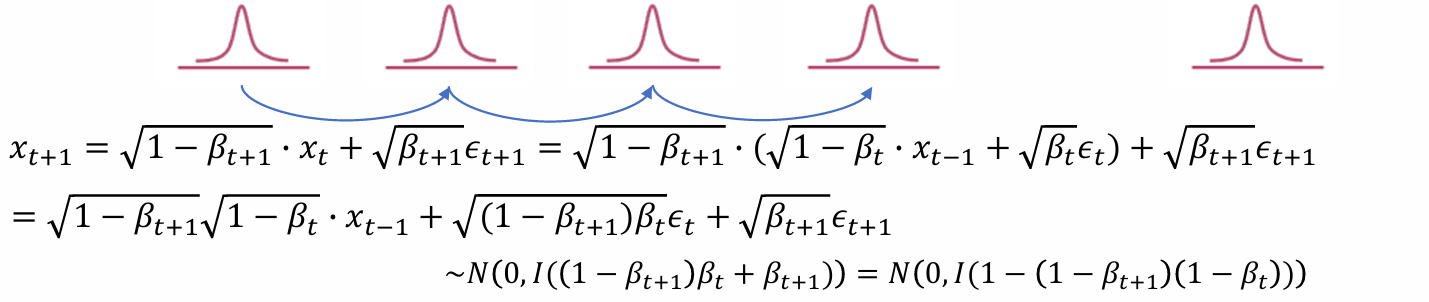
- 可以使用数学归纳法推得xt+1和x0之间的关系:

- 从而可以写成条件概率的形式表示xt+1和x0关系:
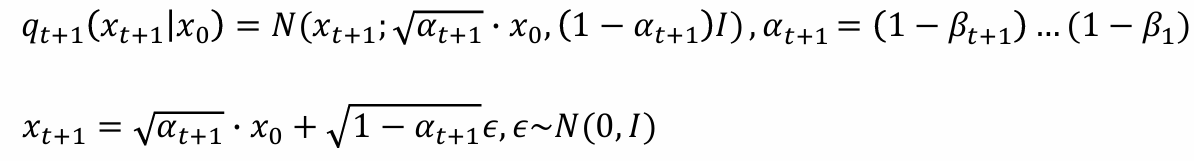
- 当t -> ∞时,αt+1 -> 0,从而xt+1 -> N(0, 1),当加噪步骤t足够多时,结果接近于N(0, 1)的高斯噪声
Backward process: reverse denoising
- 回看前向传播过程,若已知q(x0)则可以根据概率密度公式计算出q(x1):𝑞1(𝑥1) = ∑𝑞(𝑥0)𝑞1(𝑥1|𝑥0),从而可以递推计算出qT

- 前向传播给定任何image 𝑥0~q(x0),都可以得到:
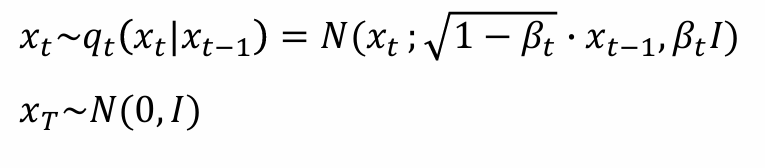
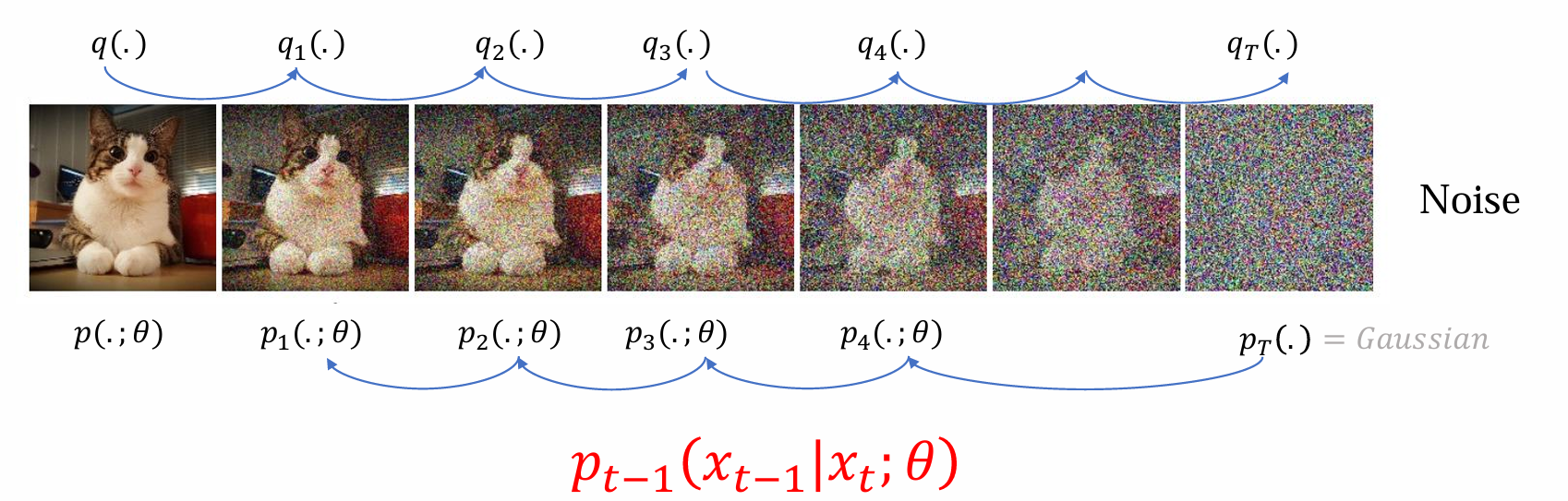
反向传播的去噪过程涉及神经网络θ,概率密度用p表示:𝑝𝑡−1(𝑥𝑡−1|𝑥𝑡;θ),最后得到由θ生成的分布
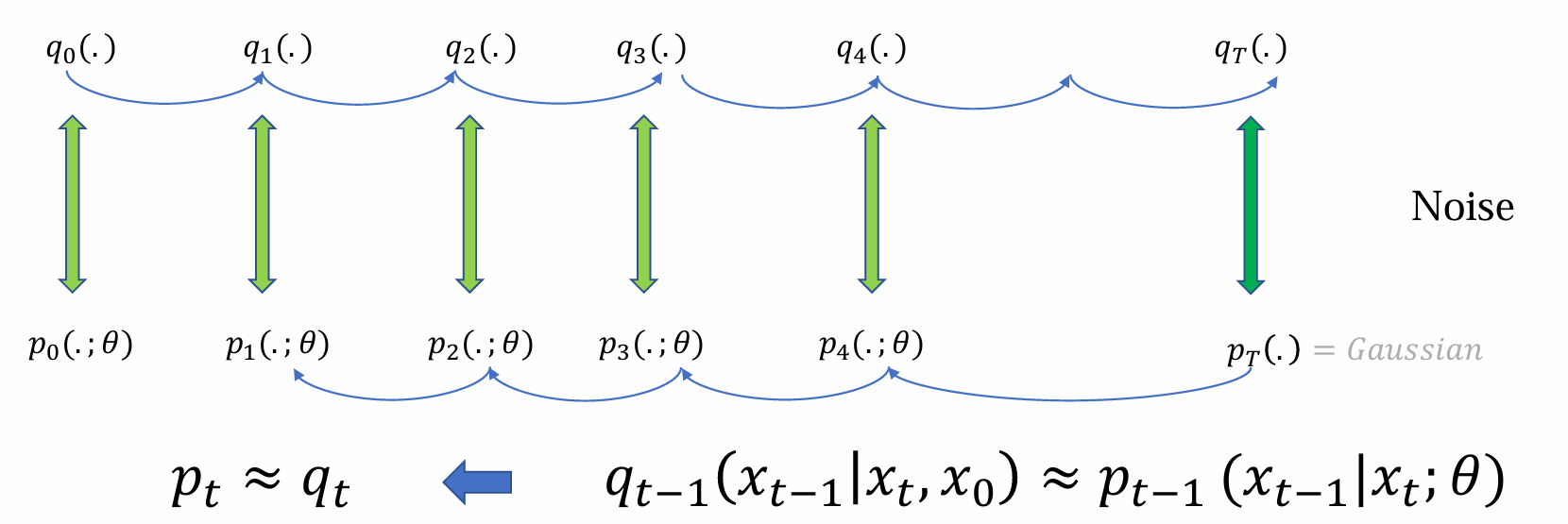
forward的最后如果T足够大可近似认为qT(.)为N(0, 1),严格等于backward的开始PT(.)
𝑥𝑡−1 ~ 𝑝𝑡−1(𝑥𝑡−1|𝑥𝑡;𝜃) = 𝑁(𝑥𝑡−1;𝜇𝜃(𝑥𝑡,𝑡),𝜎𝑡²𝐼)
q0(.)是真实data分布,p0(.;θ)是生成过程的终止,最后生成模型得到的data
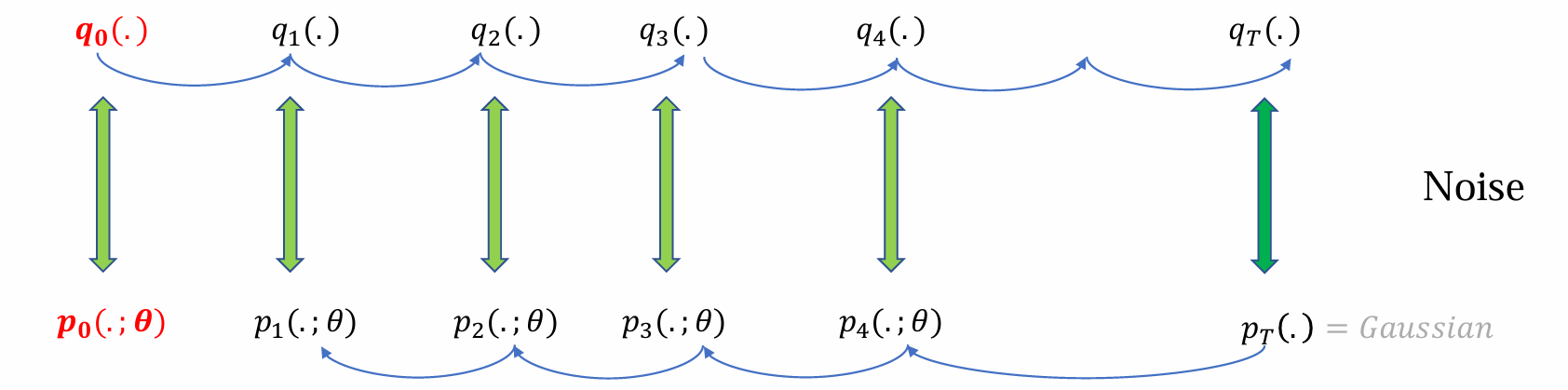
目标:希望每个时间步的p和q都尽可能接近(diffusion的核心),不仅是q0和p0相近
前向传播过程是定死的,βt和αt是不可学习的参数
问题:如何学习θ使得noise分布和denoise分布的每一步都尽可能相似
DDPM
Training
由于q(x0)位置,因此需要从中采样samples,对于每个真实data,希望计算出x0由模型θ生成出的概率大
训练目标:

- 问题:q可以显式计算,但是计算x0在p0的分布是困难的(经过若干神经网络的变换)
Training objective through ELBO
希望加入x1,x2,…等中间过程化简从而使得不可算的过程近似可算
将x1,…,xT的过程简写为z,则可有以下化简:

- 将p(x0;θ)视为x0和θ的联合分布,由贝叶斯公式可以化简为:
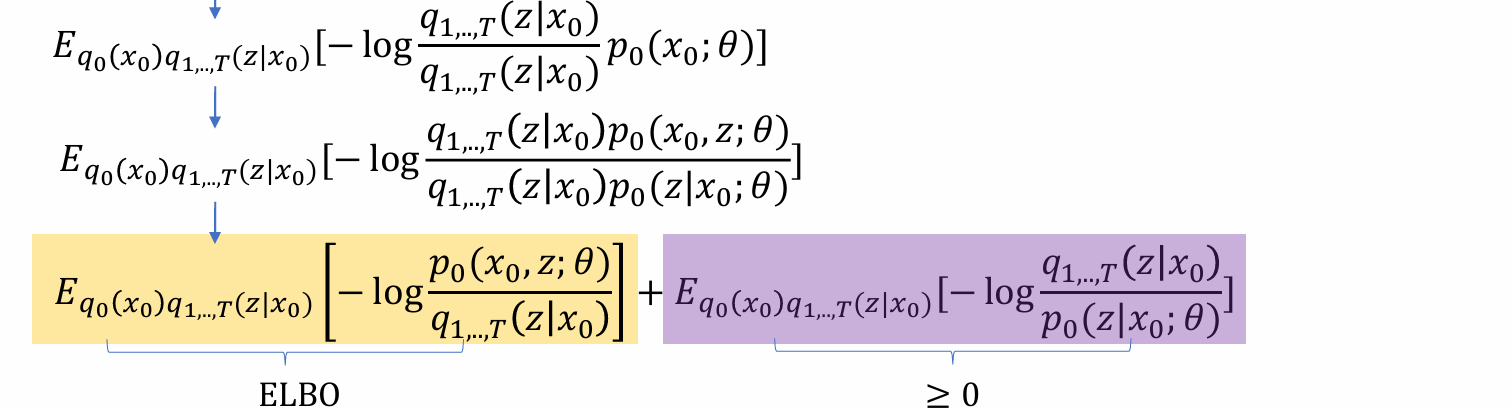
其中后式是定义在z上的两个分布,本质上是(p, q)的KL散度,≥0
因此前式是ELBO,可以通过优化ELBO来优化Training loss
Training loss
- 计算过程:从q0中sample出x0,forward出x1,…,xT,计算p和q(以下内容不考)

可将联合概率密度拆分成多个条件概率密度分布
无法计算qp,…,T(x0:xT),但是可以通过sample得出,可以把所有和q相关的序列sample出从forward process获得
-logp0(x0|x1;θ)表示给定x1,经过θ后,能否还原x0完成去噪
KL散度中后面一项表示加噪后的data能以多大概率还原加噪铅的data
KL散度两项表示已知x0,xT希望q的xT-1分布和P的xT-1分布相近
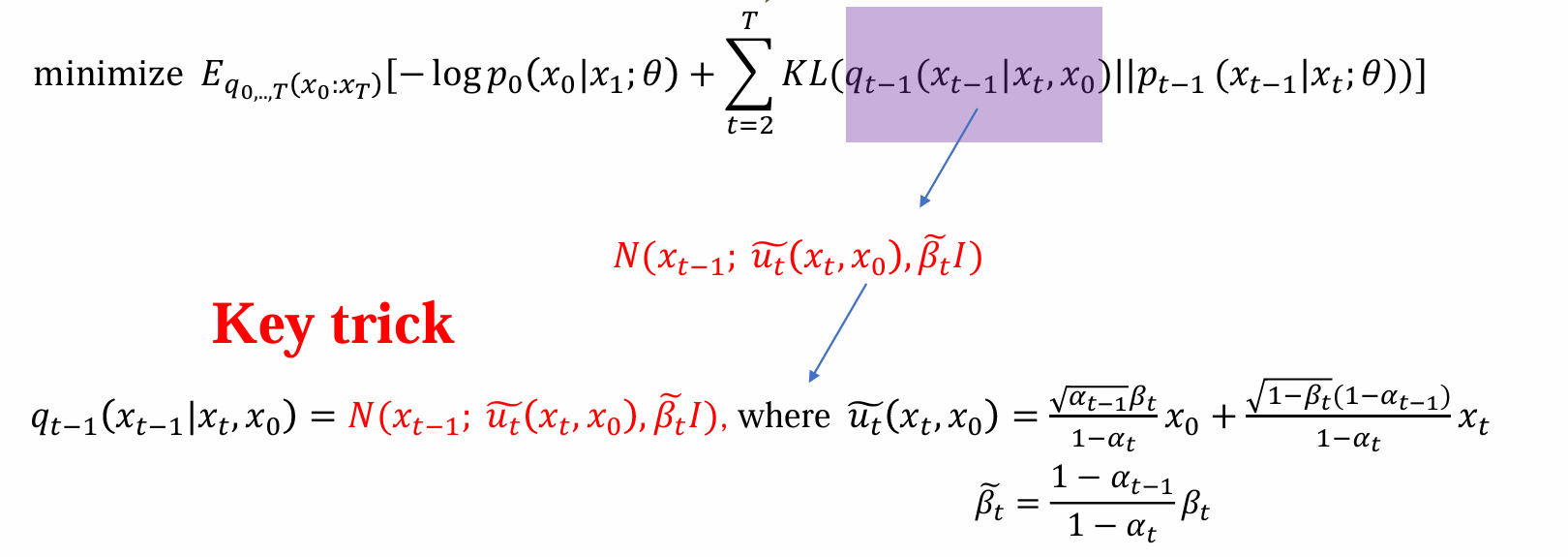

由于只关心和θ相关的(uq)进行最小化,所以可以去掉DKL(p||q)中的首尾两项
从而得到最后的优化目标:
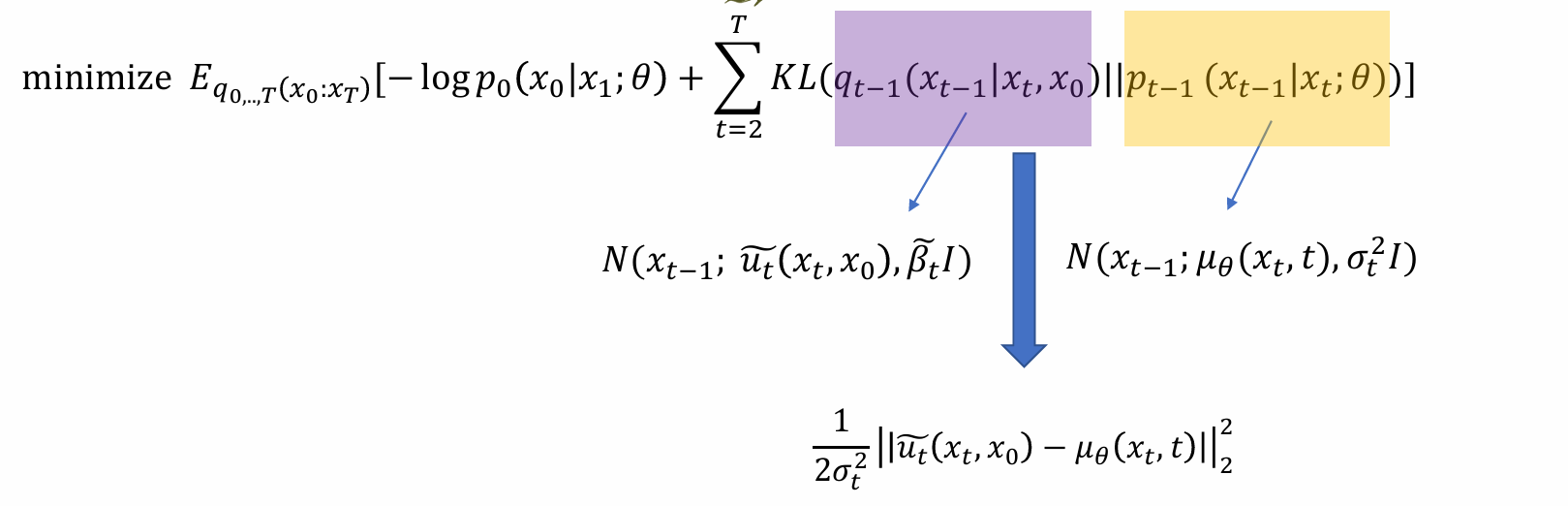
任何一个xT和x0,利用显式计算得到෦𝑢𝑡(𝑥𝑡,𝑥0),再用神经网络计算uθ(xt, x0),希望二者尽可能相似
DDPM loss的本质:
Reparameterization
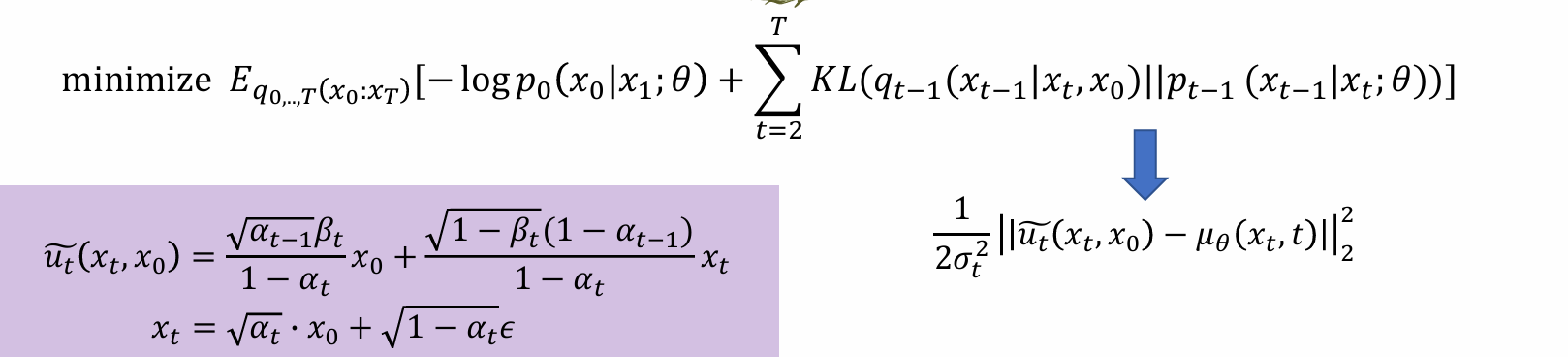
化简目标是均值相减的二范数
问题:ut(xt, x0)和t, x0, xt相关,计算复杂;而uθ之和t, xt相关无需x0,因此希望ut的计算也能去掉x0
forward pass推导出的x0, xt关系,αt和t相关,t越大,αt越小。可以用xt消掉xo
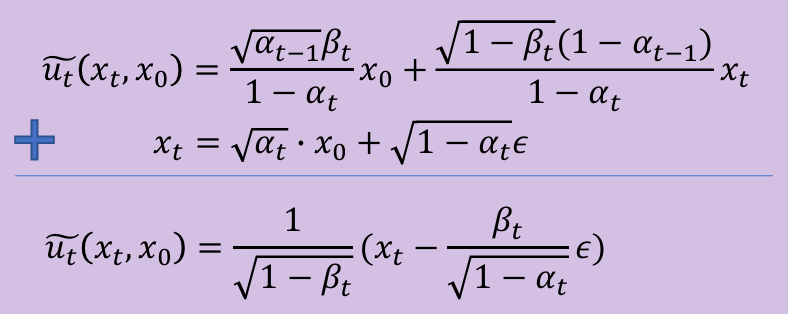
- 希望后式的形式参数化和前式相同,只有𝜖作为神经网络学习的目标:
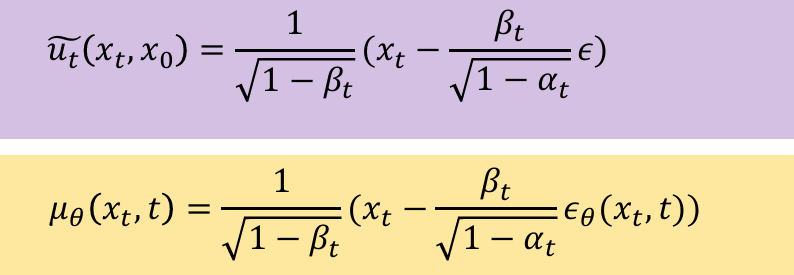
- 从而带入优化目标可化简得:
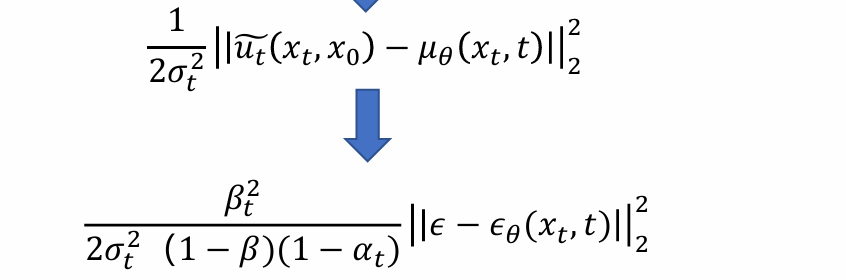
model去噪方法:
- 利用model去噪,重建去噪后的image
- 用模型预测噪声,生成噪声,减去噪声得到image
优化目标中的模型预测的是噪声,使用的为第二种去噪方法

- 模型和xt, t相关,其中t决定加噪的强度,问题:模型该如何构建?用什么模型结构?
Implementation consideration——architecture
输入是加噪后的image xt,输出是噪声的方向。可以选用U-net和transformer架构的模型
问题:如何加入t的信息
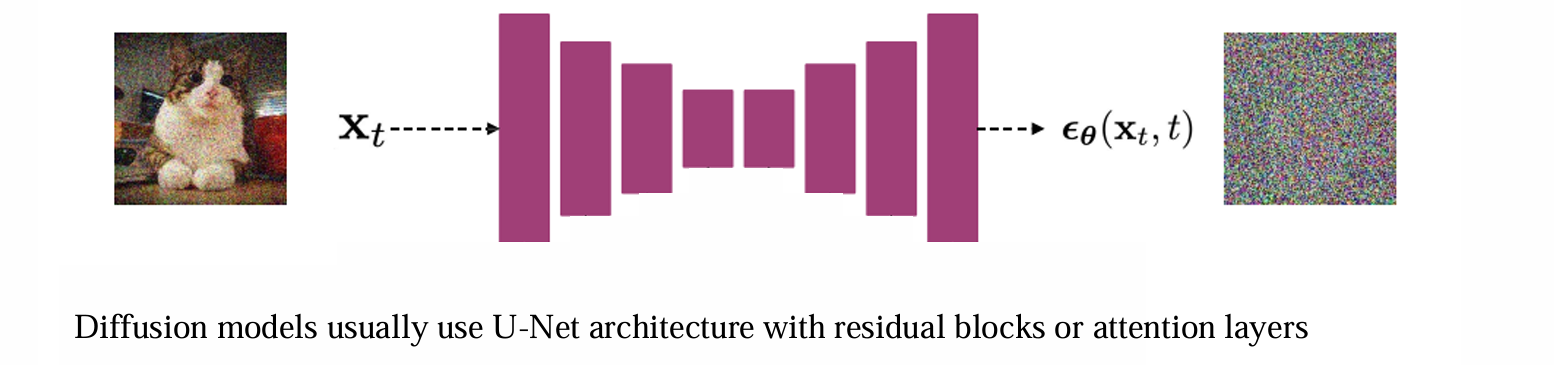
由于θ处理的使高维数据,而t是一维的,因此需要先将t映射到高维空间(e.g. sin, cos)
然后再把映射后的t在不同频率上展开,将t的信息插入到每一层中
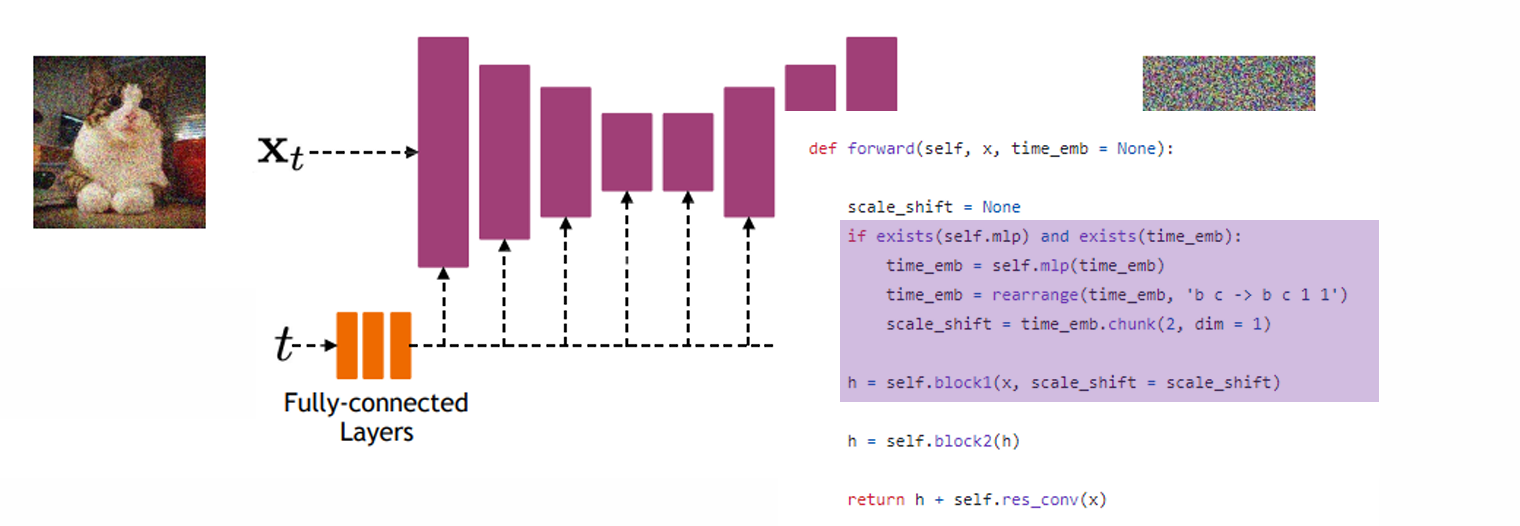
- summary of DDPM(核心:预测noise和加的noise一样)

Connection between DDPM and score function
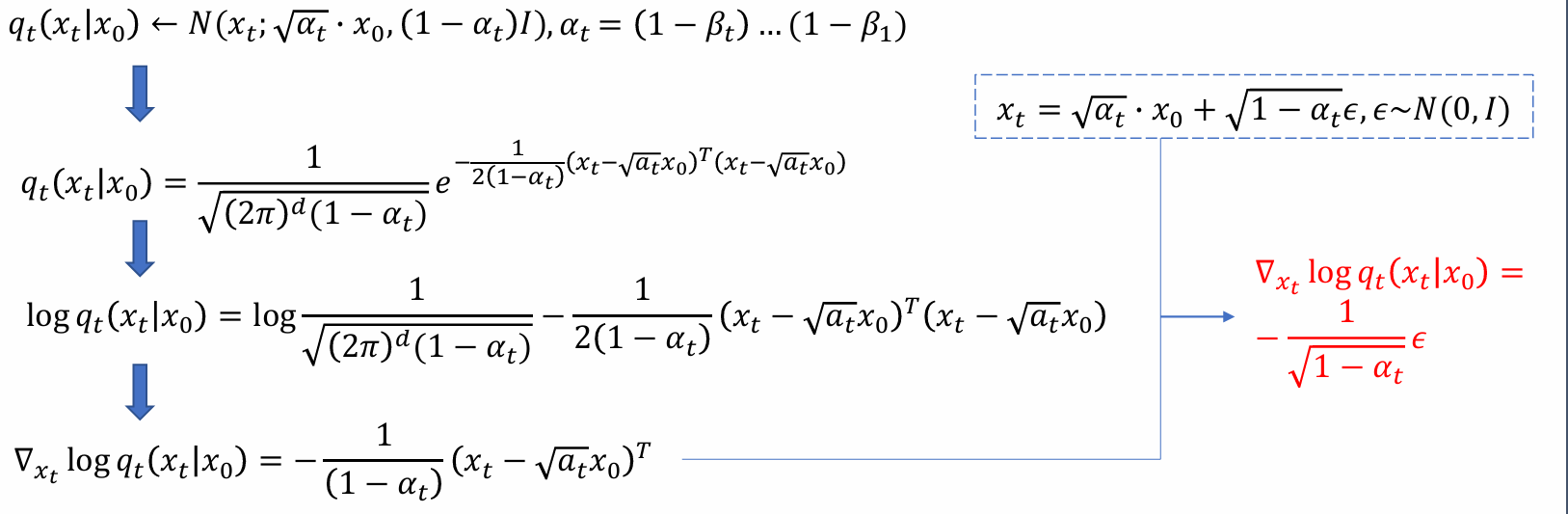
score function:先取对数,再对关心变量求导
预测目标:再t时刻match对应的score function
score function指的不是match image(data)的score function,而是在forward过程中任意t时刻的score function,𝜖θ需要与之对应
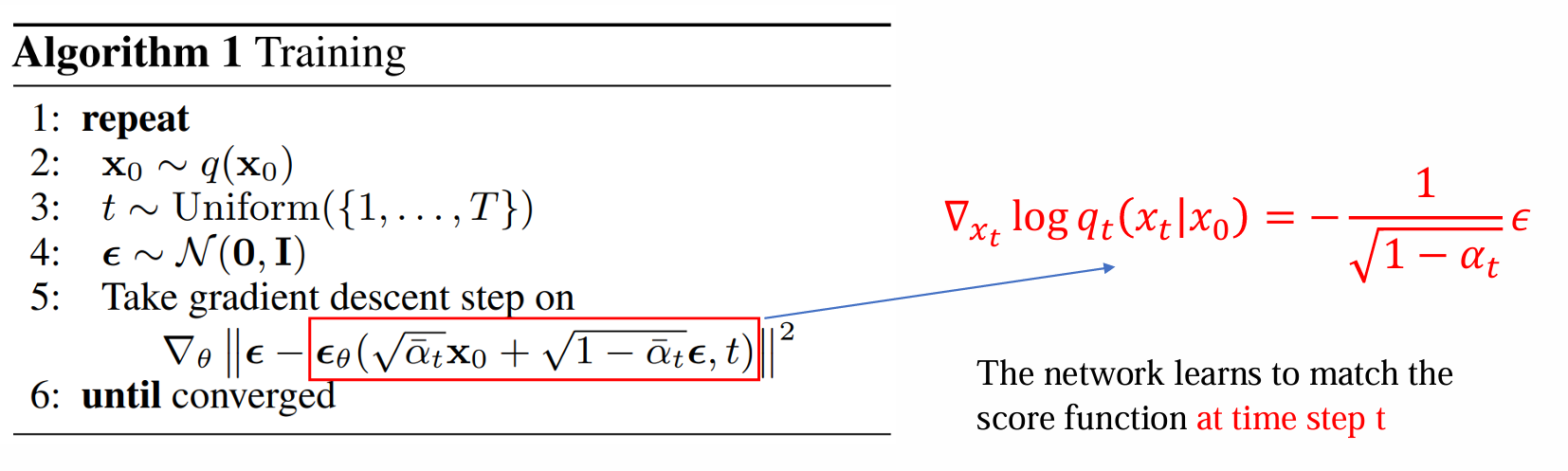
Understand DDPM through stochastic differential equation(随机微分方程)

Infinite-step DDPM
加噪过程是不断加入小的噪声,希望将其连续化,变成无限步
离散化 -> 连续化:取很大的T,再每个时间步t,计算t/T从而映射到[0, 1],当T足够大时可以认为是无限的,连续的
此时关心的x的范围从R变为[0, 1]
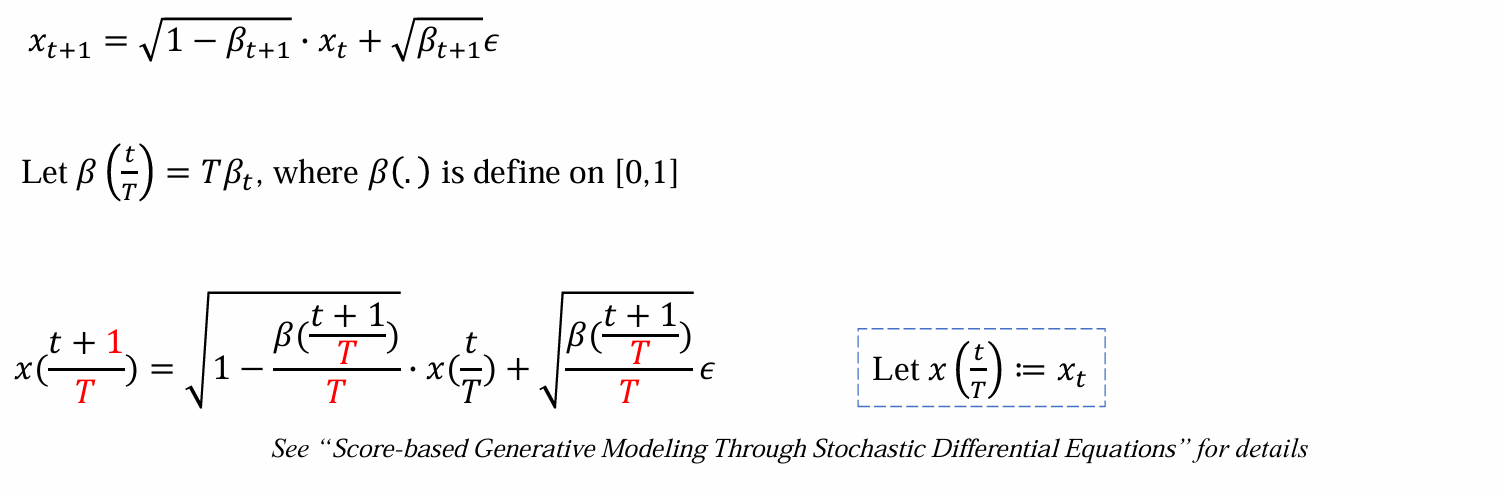
- 考察(x+1)/T,1/T可以写成无穷小量δT,t/T重参数化为t,可以化简为:
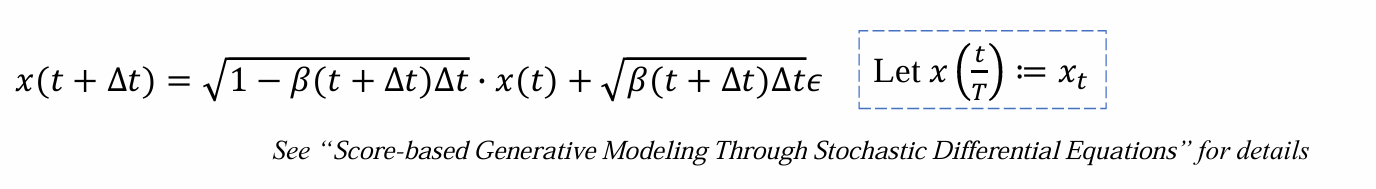
- 做泰勒展开,将高阶无穷小量(δt²)约去,代入x(t+δt)-x(t)=dx(t)可得:

上式称为连续时间马氏过程
问题:上述操作仅涉及forward pass,但是实际上优化关心的是backward pass
The generative reverse stochastic differential equation
给定一个一阶微分方程和在时间 𝑡0 的初始条件:
- 估计t > t0的solution:forward
- 估计t < t0的solution:backward
本质上reverse ODE和forward ODE是一样的,只是t和δt的正负关系有变化
Reverse SDE
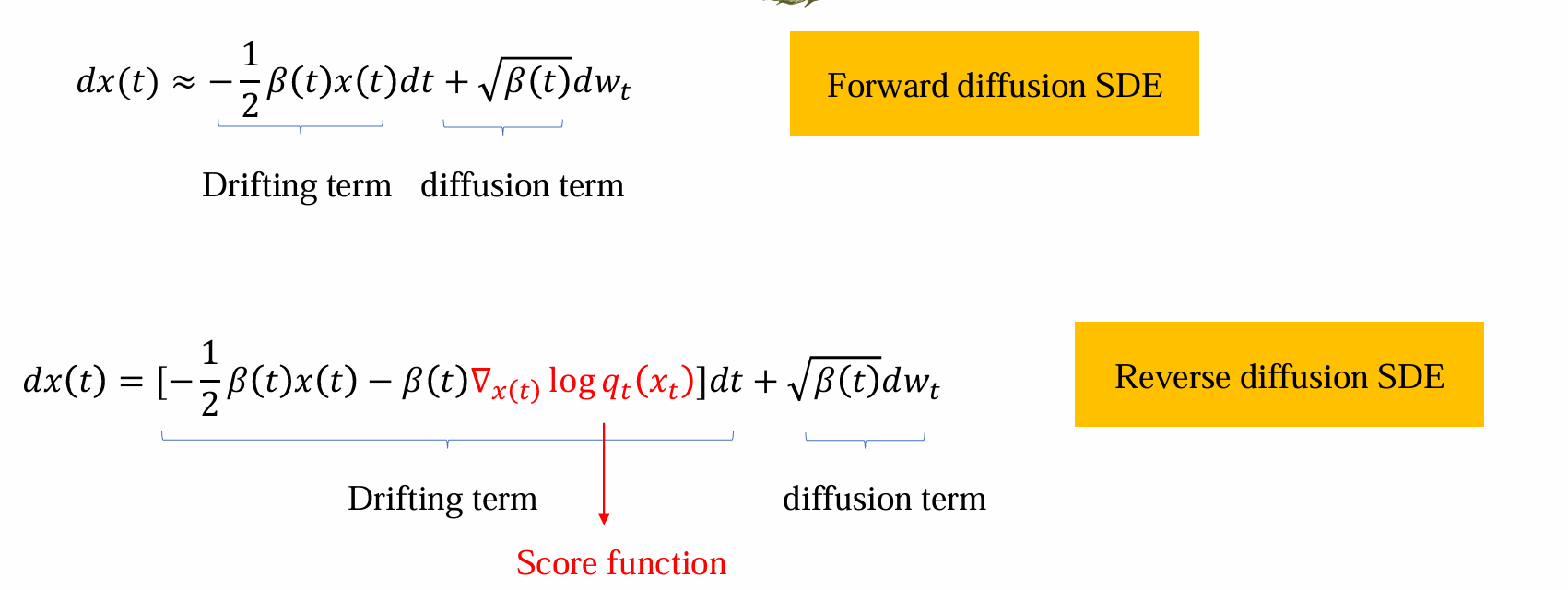
- diffusion term不变;drifting term多了一项:对qt时刻的score function
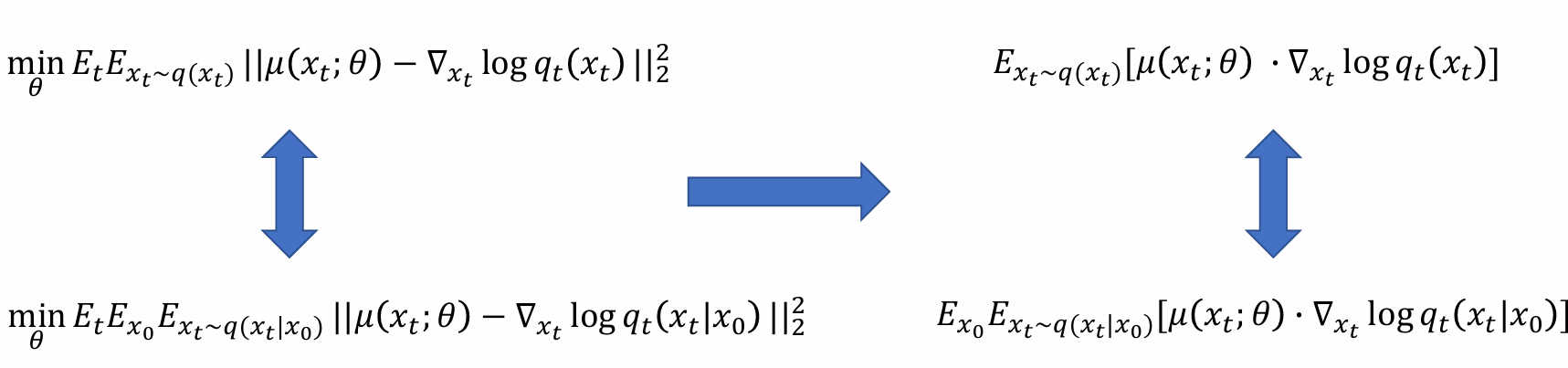
Learning model by score matching
- 由于score function无法计算,也因此需要用神经网络θ估计:
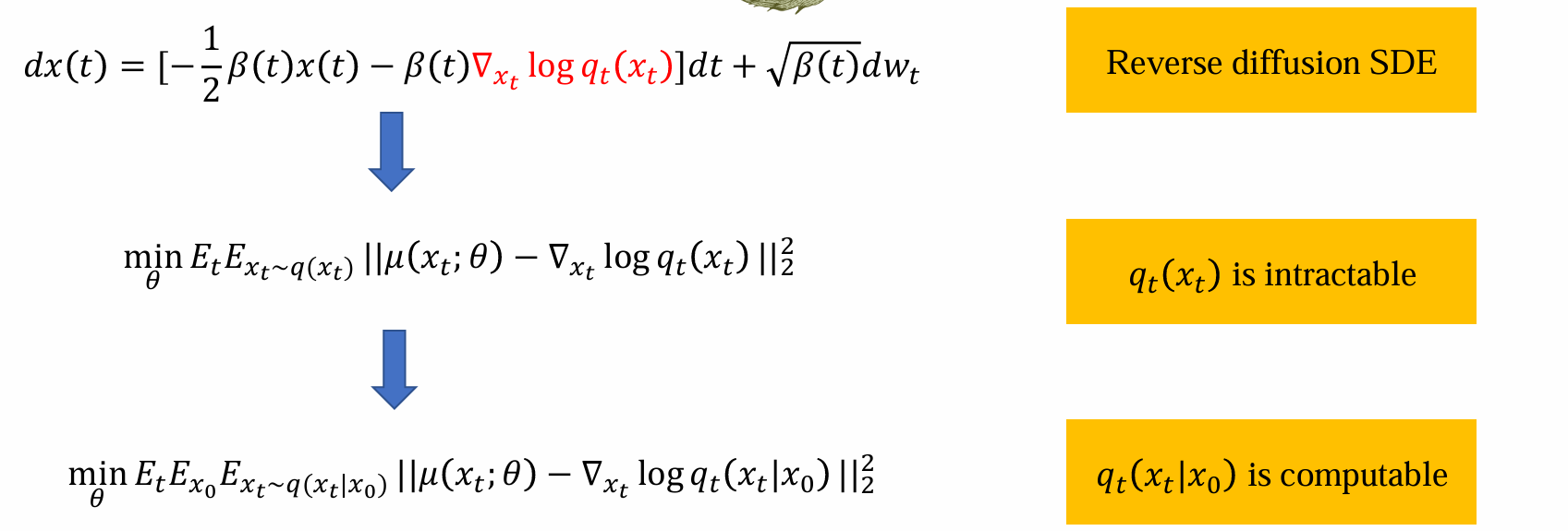
- 优化过程如下: