Generative Adversarial Networks

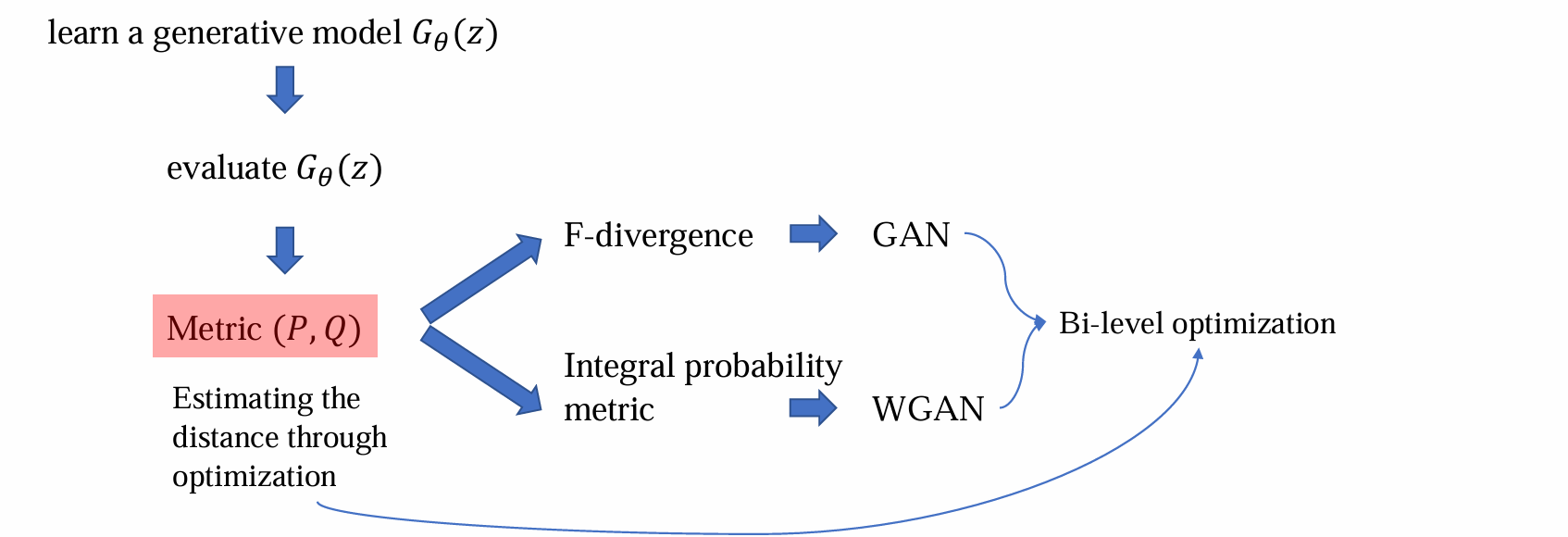
Metrics

From complex distribution to simple distribution

  • 生成模型的核心：给定随机噪声，生成想要的结果形式 e.g. text、image

  • 假设随机变量X服从一个非常复杂的无法显示表示的分布Q，我们该如何从Q中生成数据？

  • 假设我们已知Q的累计概率密度函数F(x)，F(x)有如下性质：

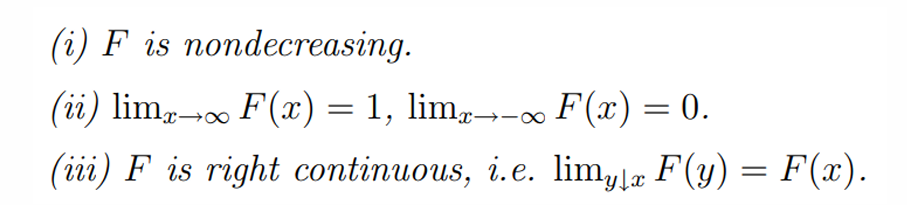
image.png

  • 假设我们可以算出F(x)的逆函数F(x)^(-1)，则可通过下面的算法采样Q：
    1. 从均匀分布中采样Z
    2. X = F(Z)^(-1)服从Q

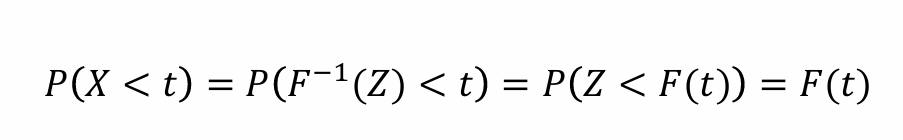
image.png

  • 代入X=F(Z)^(-1)后，X的随机性变为Z的随机性。再对等式两侧同时作用F可得𝑃(𝑍 < 𝐹(𝑡)) = 𝐹(𝑡)

  • 从而如果Q的反函数可求，可利用均匀分布采样出复杂分布Q

  • 问题：Q未知，F(x) 和 F(x) 的反函数都不可求，因而需要神经网络来解决

  • VAE问题：VAE较浅，用小网络做image generation任务时，image真实性和质量较差

  • 解决方法：可以使用GAN来实现从简单噪声中采样，经过复杂的函数变换生成image

image.png

GAN is a kind of implicit generative model

  • 生成图像的模型可以分为两类：

    1. 显式模型：
      1. 已知模型参数
      2. 给定任何数据，都可以算出其出现的概率，可以计算出数据集出现的概率
      3. 可以使用MLE进行优化
      4. e.g. AR model
    2. 隐式模型：
      1. 已知模型参数
      2. 对于每个样本，无法计算出概率密度
      3. 无法通过MLE优化，需要其他的loss
      4. e.g. VAE、GAN

  • 隐式模型问题：希望关心模型生成结果的好坏，那么该如何估计生成数据与真实数据之间的差异？

Difference metrics

  • 给定两个点A、B，可以计算两个点间的欧氏距离：𝑑 =||𝑥𝐴 −𝑥𝐵||2

  • 给定两个集合SA、SB，一种简单的办法是可以计算两个集合这种距离最近的点

image.png

  • 问题：两个集合部分重合的时候，这种距离不再适用

  • 解决方法：可以计算集合A、B中的点到集合B、A最近距离之和

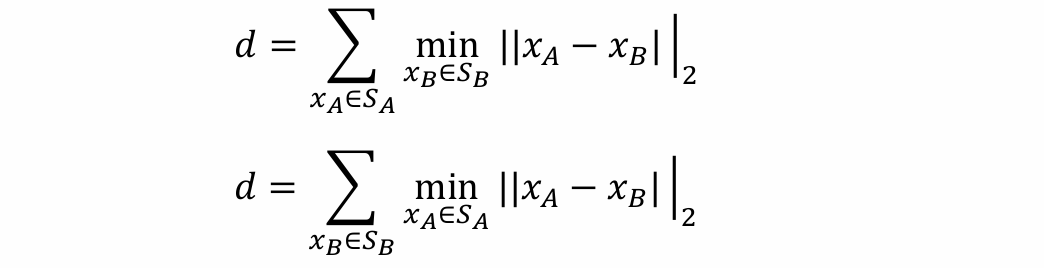
image.png

Difference between two distributions

  • 可以使用f-divergence来评估两个分布的距离

  • 将 𝑃(𝑥) 表示为一个分布（其密度为 𝑝(𝑥)）、𝑄(𝑥) 作为另一种分布（密度为 𝑞(𝑥)）

  • 函数f:[0, +∞] -> [-∞, +∞]满足性质：

    1. 凸函数
    2. 非负函数
    3. f(1) = 0
    4. 有限

  • 则f-divergence定义为：

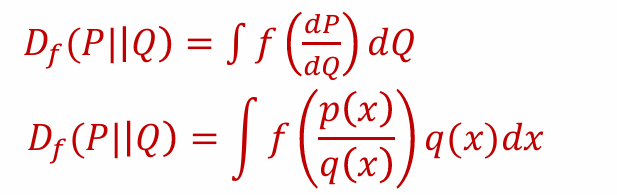
image.png

  • f-divergence不是严格意义上的距离：不满足三角不等式和对称性

  • f-divergence是非负的，证明：

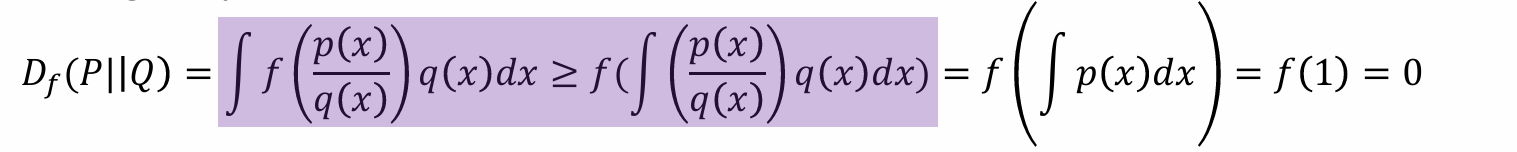
image.png

  • 函数f需要预先定义好

KL divergence

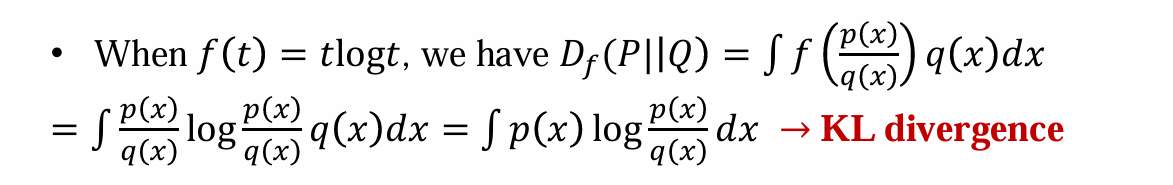
image.png

total variation distance

  • 全变差距离：对差的绝对值进行积分

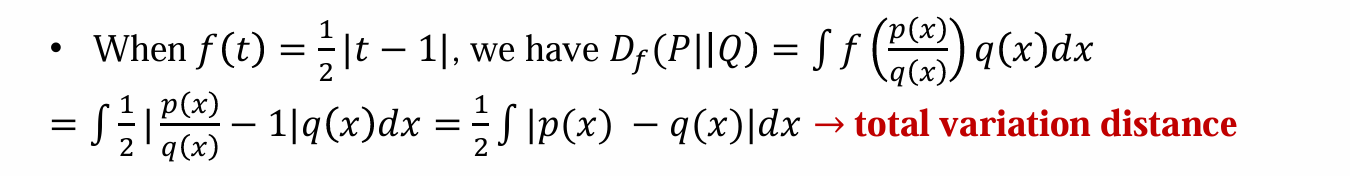
image.png

Jensen-Shannon(JS) divergence

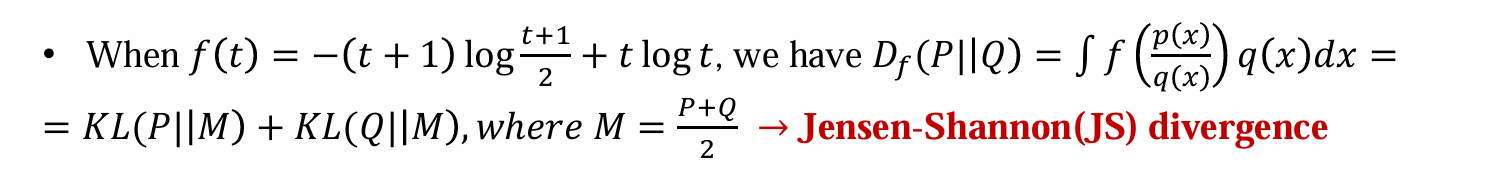
image.png

  • f-divergence作用：衡量生成数据和真实数据分布的差异有多大，从而降低这个差异优化模型，从而生成更真实的image

GAN

  • 学习生成模型（最小化）Jensen-Shannon-divergence

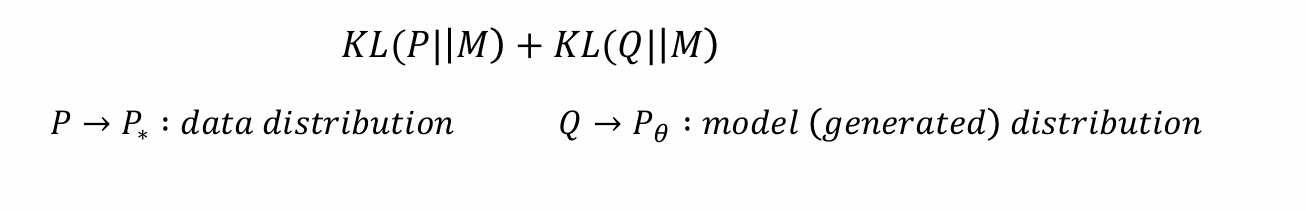
image.png

  • P∗是gt，希望逼近；Pθ是模型生成的数据，希望minimize P∗和Pθ的差别

  • JS散度希望尽可能的小：

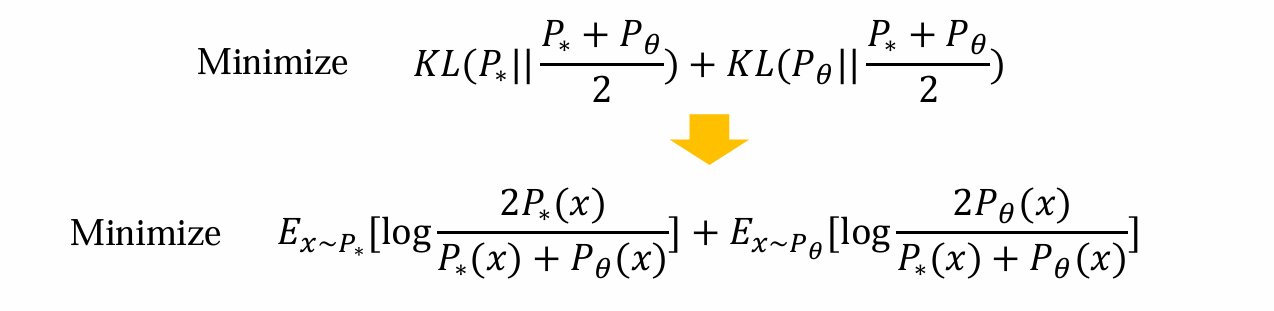
image.png

  • 前者是真实数据的期望，后者是生成数据的期望，二者形式接近但是关心的期望不同

  • 问题：难以计算P∗(x)和Pθ(x)。前者无法计算，后者经过了复杂的神经网络，难以估计

  • 解决方法：可以从二者的物理意义入手，用其他方法做估计

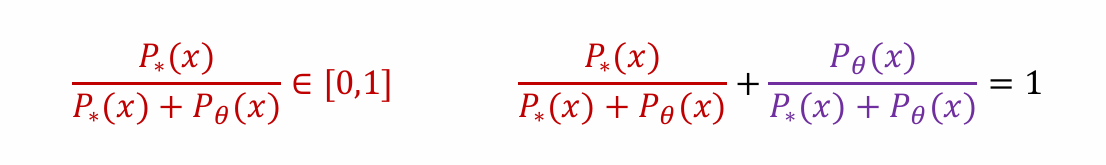
image.png

  • 观察到二者均属于[0, 1]，且分母相同，相加为1

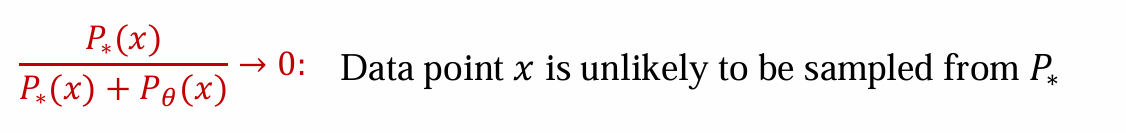
image.png

  • 说明P∗(x)趋近于0，x不太可能是从gt中采样得到

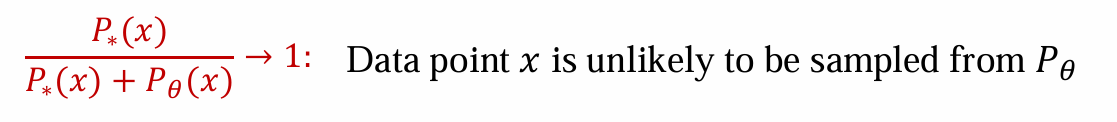
image.png

  • 反之，说明Pθ(x)趋近于0，说明x不太可能是从模型生成数据中采样得到的

  • 可见，可以构建一个二分类器Dθ’(x)来判别数据x是从gt中得到的还是从模型生成出来的：

    1. 如果认为是模型中生成出来的，则输出0
    2. 如果认为是从gt中采样出来的，则输出1

  • 目的：由于P∗(x)和Pθ(x)无法计算，因此用Dθ’(x)的结果来代替：

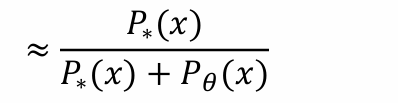
image.png

  • 替换后可得，生成模型的优化是：

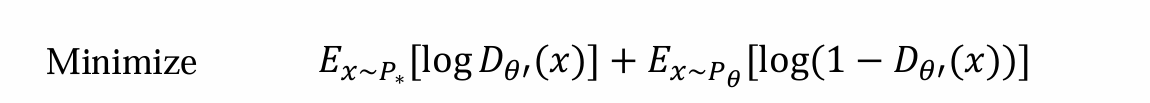
image.png

  • 训练Dθ’：假设生成模型为Gθ(z)，从噪音z中生成数据

    1. 从gt中采样K个数据：[positive, 𝑆𝑝𝑜𝑠]，希望Dθ’输出label为1
    2. 从Gθ(z)中采样k个数据：[negative, 𝑆𝑛𝑒𝑔]，希望Dθ’输出label为0

  • 则Dθ’需要优化maximize acc：前面式子是在真实数据中最对的，后面式子是在Gθ(z)中最对的

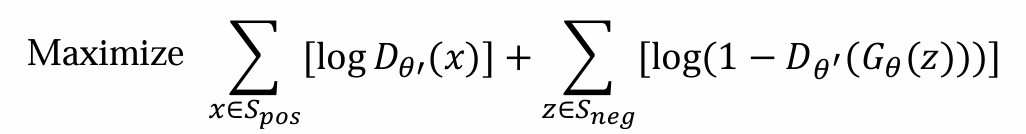
image.png

  • 训练：

    1. 从gt中采样K个数据：[positive, 𝑆𝑝𝑜𝑠]
      2，使用不同噪声z，从Gθ(z)中采样K个数据：[negative, 𝑆𝑛𝑒𝑔]

  • Gθ(z)需要优化minimize loss:前面式子与Gθ(z)无关，而后面式子希望minimize等价于希望骗过Dθ’，让其无法分别

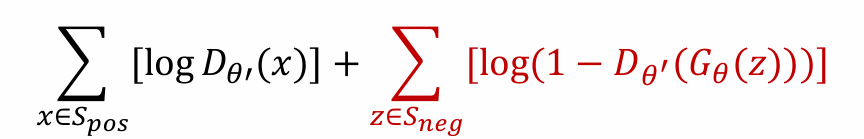
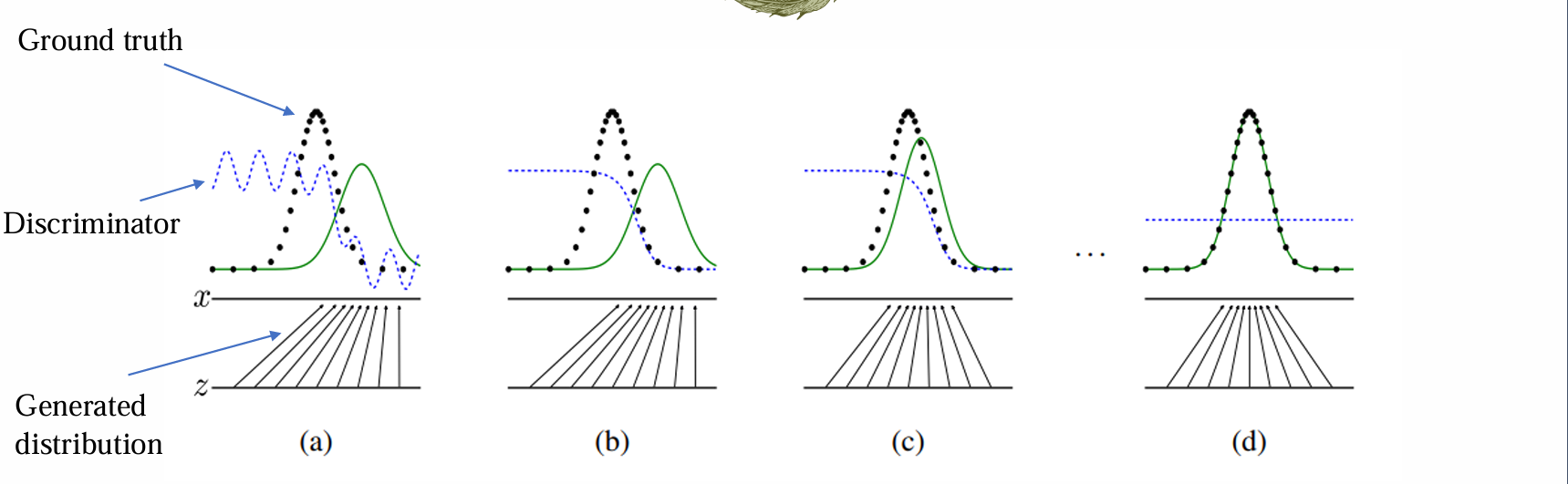
image.png

  • GAN的训练过程：

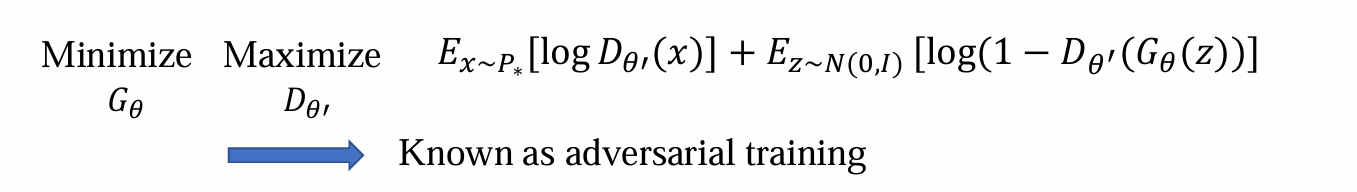
image.png

  • Dθ’的目的是为了能够计算JS散度

  • Gθ的目的是通过训练最小化JS散度提高生成质量

Overview of GAN

  • 模型Gθ可以采样数据：

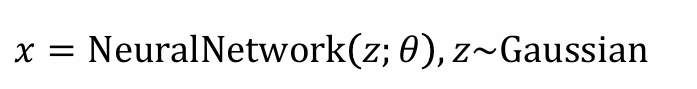
image.png

  • 希望可以评估P∗(x)和Pθ(x)之间的差异 -> 引入JS散度

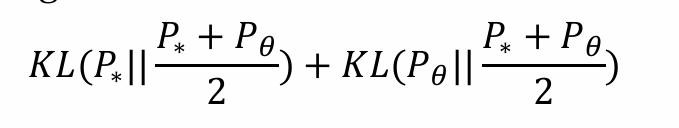
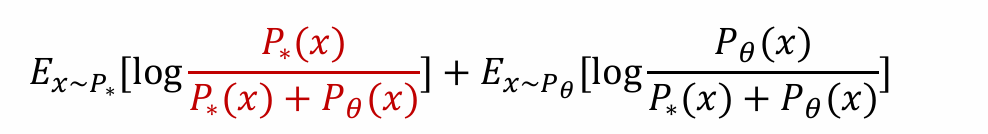
image.png

image.png

  • 因为P∗(x)和Pθ(x)不可求，根据其意义，定义二分类器模型Dθ’

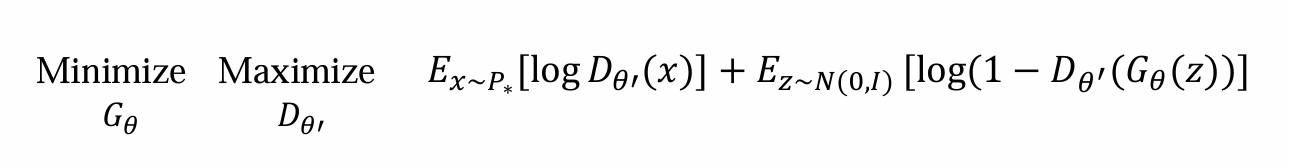
image.png

  • GAN：

image.png

Algorithm

image.png

  • 训练过程：
    1. 初始化
    2. 更新Dθ’，提高其性能，使其可以区分P∗(x)和Pθ(x)
    3. 更新Gθ，使其向gt靠拢
    4. 重复以上两步，理想状态下，直到Dθ’无法判别，收敛到输出恒为1/2

image.png

WGAN

Tough training of GAN

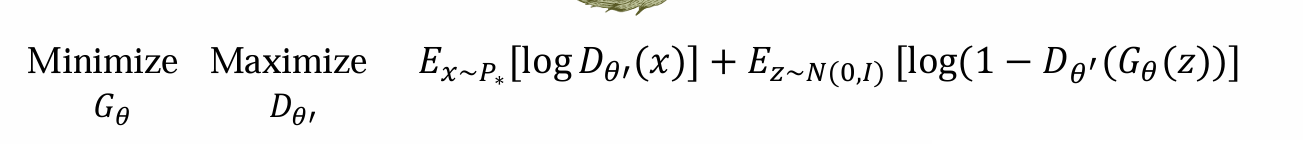
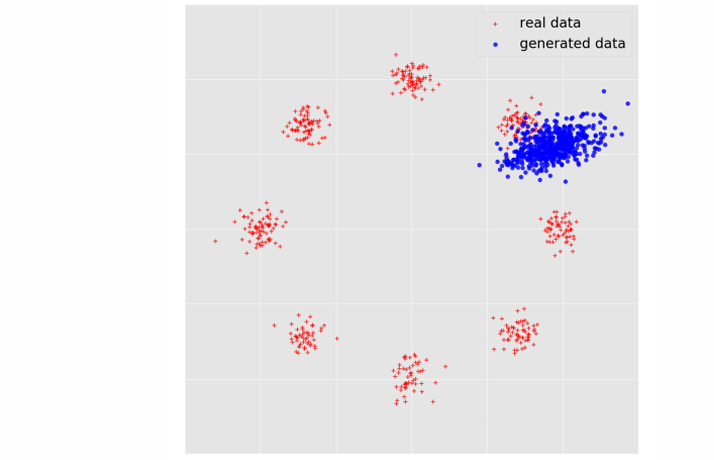
image.png

  • GAN训练中的问题：
    1. 非凸非凹，难以训练和优化
    2. G和D能力上需要相近，然而训练开始阶段D的能力往往显著强于G。G和D参数需要兼容
    3. 模式崩溃问题：只生成了一部分数据也可以使得loss很低，但是没有完成GAN的目标
      image.png
    4. 对超参数的选取非常敏感

Integral probability metric(积分概率度量IPM)

  • 动机：如果分布 𝑃 = 𝑄，对于任何实值函数 𝑓，有 𝐸_{X𝑃}[𝑓(X)] = 𝐸_{X𝑄}[𝑓(X)]

  • naive想法：若P、Q不同，则选f(x)对P、Q取期望，取绝对值度量差异 |𝐸_{X𝑃}[𝑓(X)] - 𝐸_{X𝑄}[𝑓(X)]|

  • 问题：对f的依赖严重，难以找出合适的f

  • 解决方法：取函数族F，含有多个f，遍历F取最大的绝对值差。也满足若P = Q，则DF(P, Q) = 0

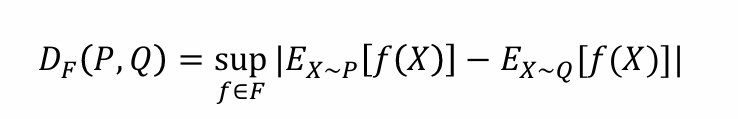
image.png

  • 问题：无法遍历F

Wasserstein distance

  • 解决方法：对F进行约束，约束F为满足1-Lipchitz函数的函数族

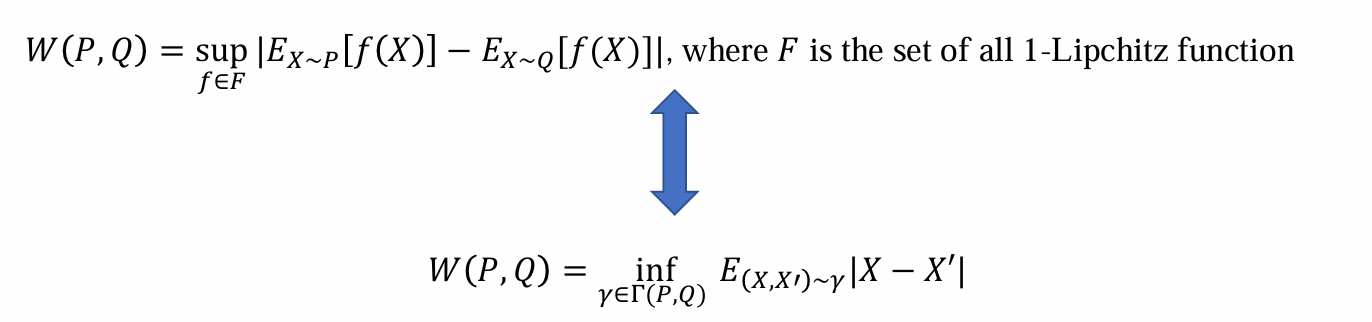
image.png

  • Γ(𝑃,𝑄)是定义在X*X上的联合概率分布，其中任意 𝛾 ∈ Γ：

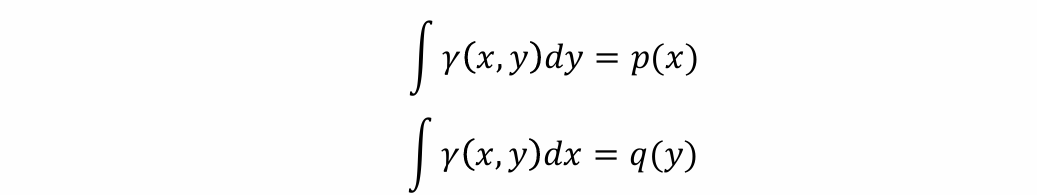
image.png

  • 注：上式应为q(y)

  • 可以借助“愚公移山”辅助理解，现在希望移动分布p(x)使其变为q(y)， 𝛾(x, y)是想要从位置x移动到位置y所移动的概率质量，然而“移动过程”本身需要对其加以限制

image.png

  • 上面的积分含义：从x移出的概率质量和原来在x位置上的概率质量分配是相同的，移出过程不增不减

  • 下面的积分含义：移过来y接收的概率质量都是从x的某个位置移动过来的，因此为对x积分

  • 假设存在一个成本函数，如果你将一个单位从 𝑥 移动到 𝑦，则成本为 𝑐𝑜𝑠𝑡(𝑥, 𝑦) = |𝑥−𝑦|，那么可得：

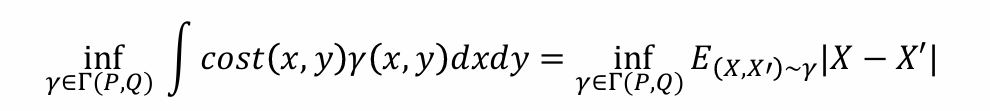
image.png

  • Wasserstein distance用于刻画物质不增不减时，如何移动cost最低

WGAN

  • WGAN的核心思路：使用 Wasserstein distance作为评估标准训练生成模型

  • 问题：依旧无法遍历F，不可算

  • 解决方法：利用神经网络，引入critic网络。本质上是遍历F取最大值(Wasserstein distance定义)，则可以用梯度上升优化

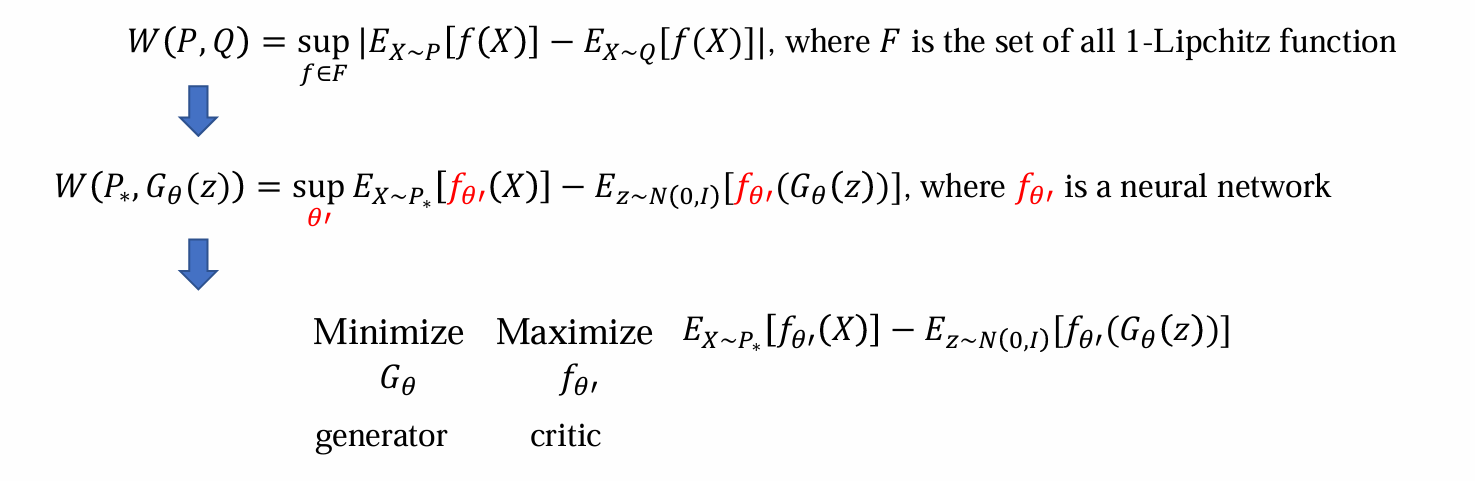
image.png

  • 化简技巧：绝对值取max，可以脱掉绝对值取max

  • minimize：希望生成的data和真实分布尽可能的接近

  • maximize：希望更好的估计 Wasserstein distance

  • 问题：神经网络刻画的f和1-Lipchitz函数计算可能完全不同，从而无法准确描述函数族F，因此需要对神经网络加以约束

  • 性质：在有界闭域上的连续函数具有有限的Lipschitz常数。参数θ’是有限闭集且连续，因此可以使用weight clipping限制参数范围

image.png

  • 做完梯度上升后clip，使其限制在一个范围内，从而使得Lipchitz有限

  • 问题：仍然无法控制Lipchitz系数，现在只是有限，而不一定为1

  • 解决方法：使用Gradient prnalty，1-Lipchitz函数指的是||f(x)−f(y)||≤|x−y|,∀x,y，即任意两点斜率不超过1

  • 因此在优化中，只希望在导数小于等于1的神经网络优化，而不在导数很大的地方对神经网络优化

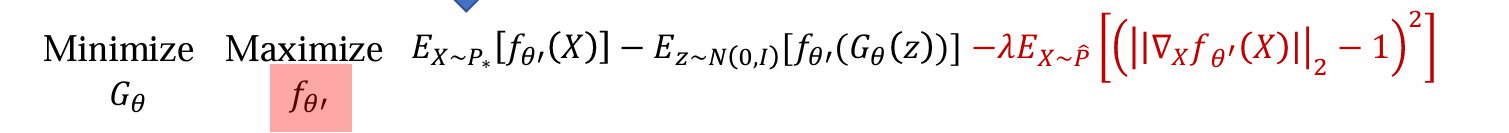
image.png

  • 上式在Lipchitz系数很大的位置，-1取平方后的值很大，从而不进行优化，只在距离1比较近的地方计算Wasserstein distance

  • WGAN的优势：训练稳定

Overview of the design philosophy

image.png