可视计算与交互概论 notes整理第8-11章
第八章 几何表示
- 在几何部分,如何表示空间中的几何体是贯穿其中的主题
几何表示:描述三维物体的形状
- 计算机中表示几何体的常见方法:
- 显式表示方法:点云 (point cloud)、多边形网格 (polygon mesh)、细分表面 (subdivision surface) 等显式表示方法
- 隐式表示方法:水平集 (level set)、代数曲面 (algebraic surface)
多边形网格模型
多边形网格模型通过记录顶点和多边形来表示几何体的表面
多边形网格模型是由一组顶点、边和面组成,这些定义了物体的形
状,由顶点列表、边列表和面列表构成。- 顶点是 3D 空间中的单一点
- 边是连接两个顶点的线
- 面是边的封闭环。面通常是三角形或四边形,并可用于表示曲面或其他复杂形状
欧拉定理:多面体的顶点数 v、边数 e、面数f 满足 v - e + f = 2
多边形网格相较于其他几何表达有很多优点:
- 容易理解和使用,也能十分简便地进行渲染和几何形状处理
- 非常通用,它可以用来创建各种形状,从简单的立方体到复杂的角色
- 可扩展性高:可以用于创建 3D 打印模型,以及逼真的动画和模拟
如果要使用网格模型表达光滑的曲面,则需要大量的面片才能让模型变得精细
三角网格
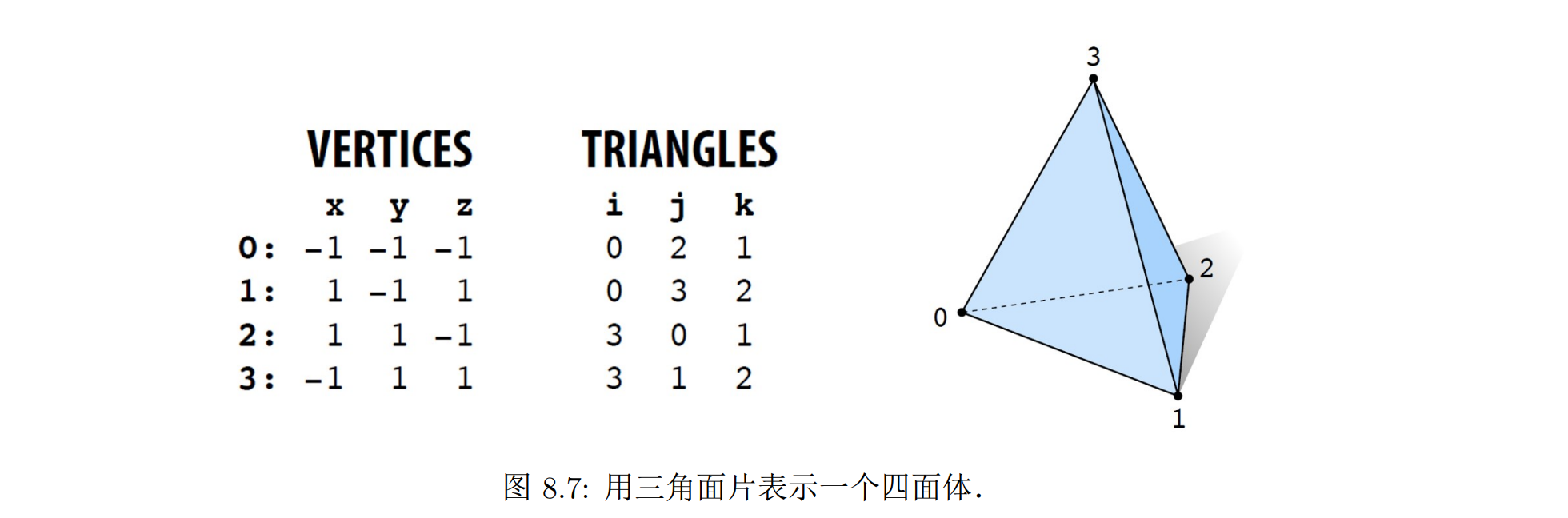
三角网格是最常用的几何表示方式,通过记录组成每个三角面片的顶点坐标,可以唯一表达一个几何体
一种常见的表示三角网格的数据结构是分别记录所有顶点的三维坐标,以及每个面片的三个顶点的下标
例如一个四面体就可以按照如下的方式进行记录。这种数据结构通过共享顶点位置,减少了存储占用,同时保证了网格的整体性,即改变一个顶点在 3 维空间中的位置可以让与该顶点有关的所有三角面片发生移动
四边形网格
- 四边形网格也是较为常用的一种网格表示,所有多边形面片全部是四边形构成,优点:
- 结构规整,易于存储
- 其四边形特性在纹理映射贴图时的计算非常方便
几何表面细分
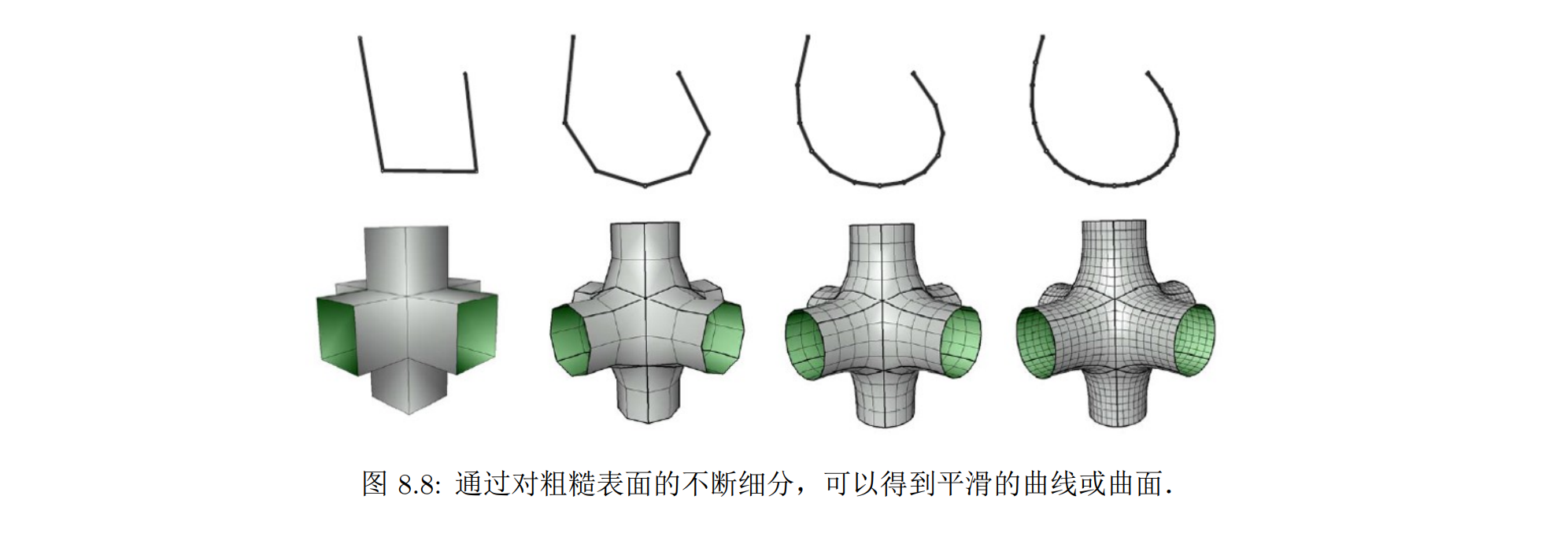
通过增加组成几何表面的网格面片数量,减小每个面片的面积,可以使几何表面看起来更加光滑
网格细分 (mesh subdivision):也称为网格的上采样,是指通过反复细分初始的多边形网格,不断得到更精细的网格的过程
Catmull-Clark 细分
Catmull-Clark 细分是最常用的几何表面细分方法之一,通过将表面的多边形细分为更小的多边形,用相邻的顶点重新定位先前的顶点,对三维多边形网格表面起到平滑效果
Catmull-Clark 细分法采用网格中包含的每一个原始多边形,并将多边形细分为四边形,基于平均值构建新的顶点,并根据周围环境调整原始多边形的先前顶点
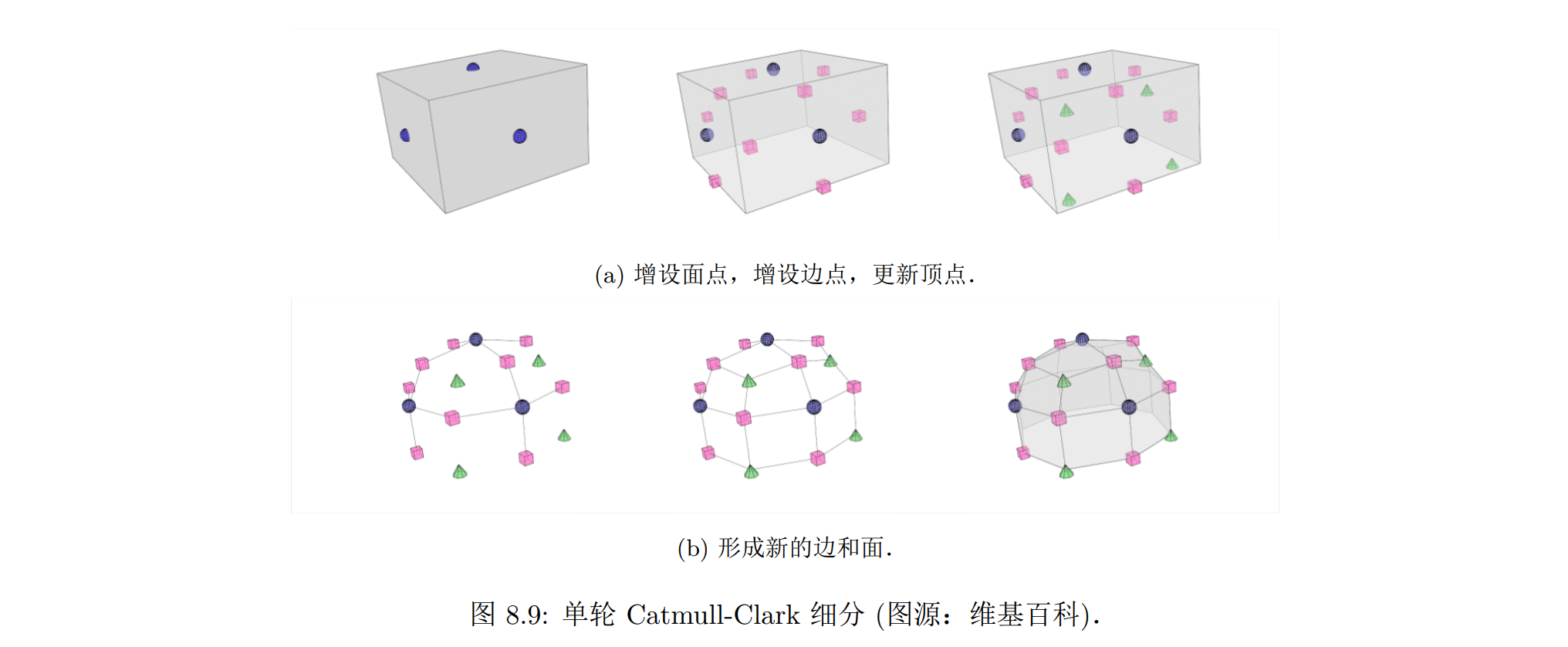
Catmull-Clark 算法每一次细分由增设面点(face point)、增设边点(edge point)、更新顶点 (vertex point)、形成新的边和面四个步骤组成
- 增设面点:对多面体的每个面片计算一个面点,这个面点是这个多边形面上所有顶点坐标的平均值
- 增设边点:对多面体的每条边计算一个边点,找出该条边的两个端点和共享该条边的两个面的面点,对这四个点的坐标取平均
- 更新顶点:对于多边形原有的每个顶点 v,使用(1)所有包含顶点 v 的边的中点 (注意不是上述步骤中的边点) 的平均值 R,(2)所有包含顶点 v 的多边形面片的面点的平均值 F,(3)以及顶点 v 的原有值的加权平均值来调整其三维坐标.加权平均遵循以下公式:
F + 2R + (n − 3)v / n (其中 n 是面点的数量) - 形成新的边和面:将每个面点连接到所有构成了它所在的原始面的边的边点,将每个新顶点连接到所有连接着它原始点的边的边点.新的面就由这些边包围而成
不论原多边形网格是何结构,新得到的多边形网格将只由四边形构成。在不断细分的过程中,表面会不断趋向平滑和圆润
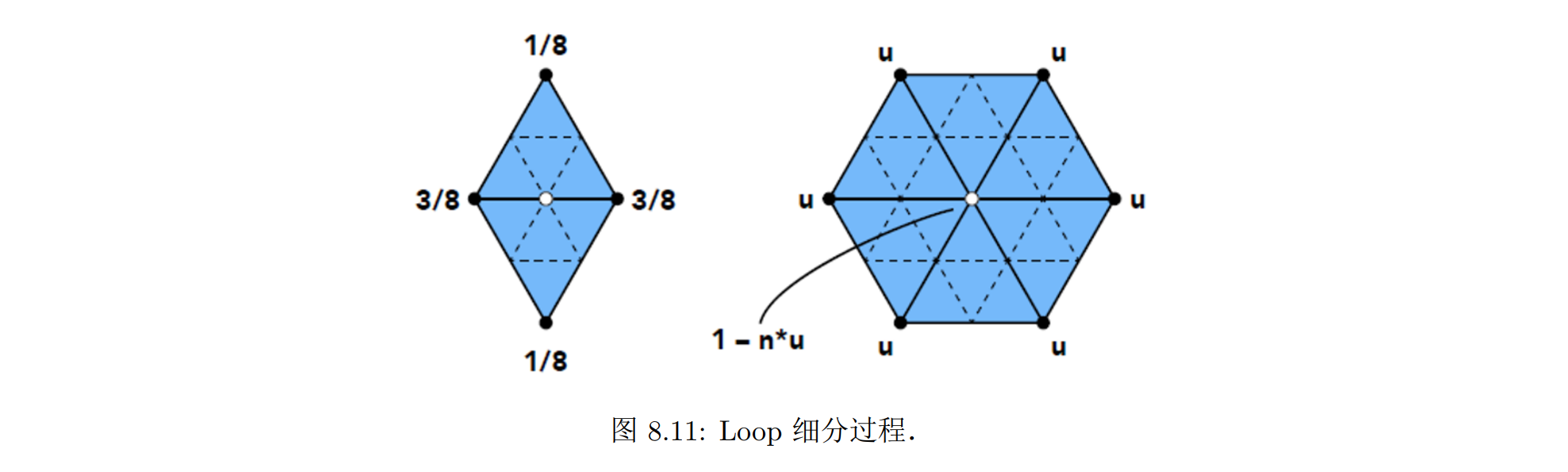
Loop 细分
Loop 细分是常见的针对三角网格模型的细分方法。每一次细分将三角面片细分为四个更小的面片,迭代下去使几何表面变得平滑
Loop 细分的过程由计算新顶点和更新原有顶点两步组成:
- 计算新顶点:
- 对于每一条边,如果这条边被两个三角形面所包含则由这条边的两个端点 v0, v2 和“跨过”这条边的两个顶点 v1, v3 加权平均计算出新顶点 ep
ep =3/8(v0 + v2) + 1/8(v1 + v3) - 如果这条边只被一个三角形面所包含(即为边界上的边),则直接取这条边的中点作为新顶点
- 对于每一条边,如果这条边被两个三角形面所包含则由这条边的两个端点 v0, v2 和“跨过”这条边的两个顶点 v1, v3 加权平均计算出新顶点 ep
- 更新原有顶点:对于每个原有顶点 v,根据以下公式更新后的位置 v′
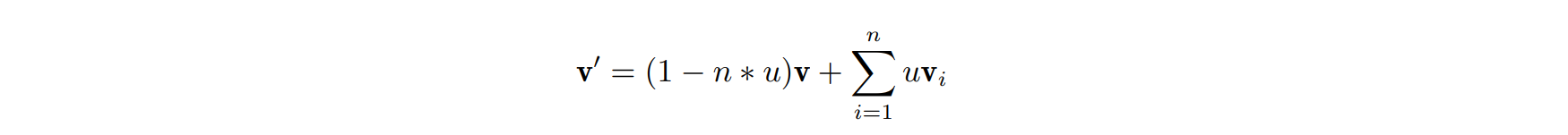
其中 n 为顶点 v 的度数,vi 为与 v 有边相连的顶点,当 n = 3 时 u = 3/16,否则 u =3/8n
- 计算新顶点:
通过不断地生成新顶点和更新原有顶点,每一次细分后连接新顶点与原有顶点,三角面片变得更加精细,得到的几何表面更加平滑
网格参数化
- 网格参数化 (mesh parameterization)是将三维和二维联系起来的桥梁
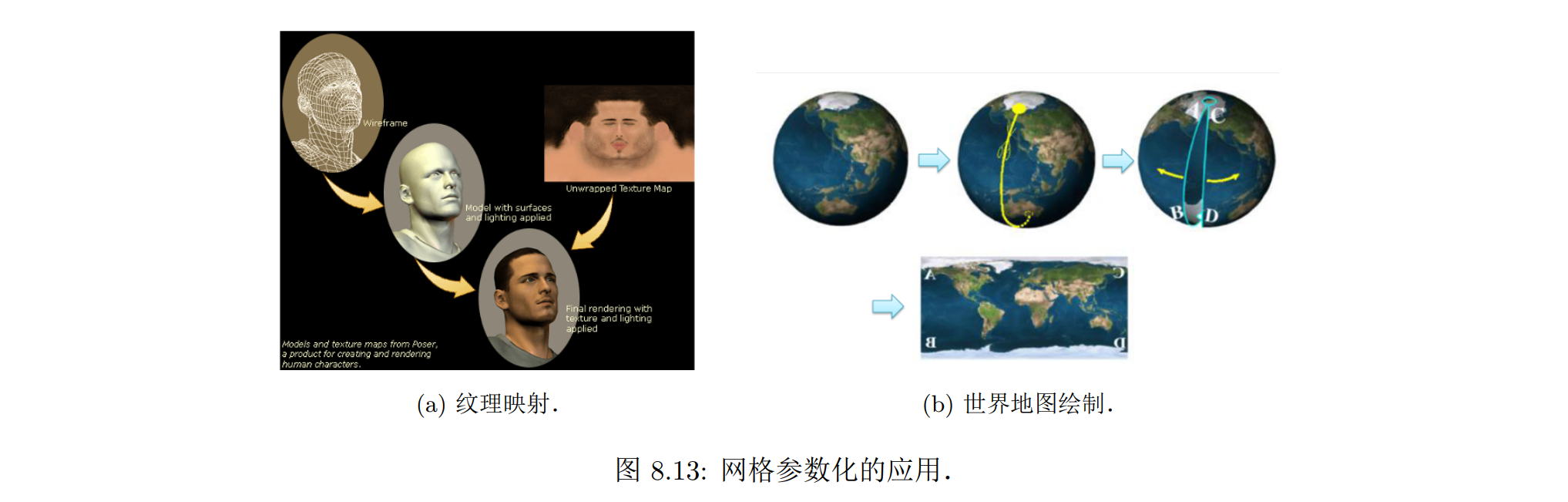
纹理映射技术:通过二维纹理空间和三维曲面之间的对应关系,计算三维曲面上每一点颜色值。这个过程需要建立三维曲面和二维纹理平面之间的一一映射,也就是参数化的过程,即计算三维空间曲面的每个网格顶点对应的两个纹理空间中坐标值 (u, v)
参数化的另一个具体应用是世界地图的绘制.通常可以采用球面坐标系来表示地球表面的每一个点,给定半径后,每一个点对应着唯一一组方位角和仰角。但实际中地球是在平面上画出的,典型的有立体投影 (或球极平面投影)、墨卡托投影和朗伯投影等方法
- 球极平面投影:将一个圆球面通过指定极点射影至一个平面的映射.能够保持角度不变,但是面积会发生改变,尤其在极点附近
- 墨卡托投影:投影后经线是一组竖直的等距离平行直线,纬线是垂直于经线的一组平行直线。各相邻纬线间隔由赤道向两极增大。一点上任何方向的长度比均相等,即没有角度变形,而面积变形显著,随远离标准纬线而增大。该投影具有等角航线被表示成直线的特性
- 朗伯投影:一种等面积的平面投影,它不仅可以精确记录面积,也能不改变方向,一般用于绘制精度要求较高的地质图或导航图
平面参数化的分类:
- 开网格参数化,这种情形下网格是具有边界的开网格,又分为固定边界映射和自由边界映射
- 闭网格参数化,这种情形下网格构成一个封闭曲面,通常人为指定一条边界将封闭网格切开,然后转化为开网格进行参数化
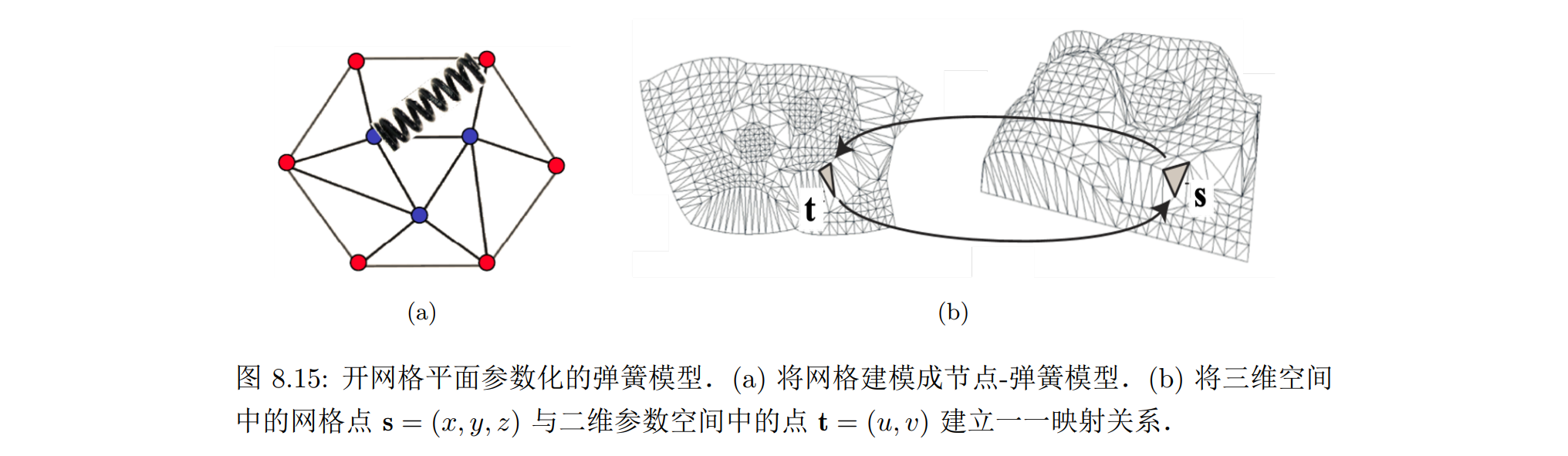
弹簧模型
开网格的平面参数化中,最基础的模型是弹簧模型:网格顶点作为图节点,网格边作为连接节点的边,形成多个弹簧连接的一个整体
建立从网格到纹理空间的参数化映射,也就是将每个网格顶点 si = (xi, yi, zi) ∈ R3 映射成二维参数空间中的点ti = (ui, vi) ∈ R2,可以采用弹簧系统的能量函数来描述参数化后的系统状态:弹簧的拉伸最后会达到平衡状态,使得整个系统能量最低,这个状态也就是参数化的最终结果
- 总能量定义为加权的弹簧能量:其中 n 是节点总数,Dij 是连接第 i 和第 j 个顶点的弹簧的劲度系数,也是其所对应边在系统中的权重
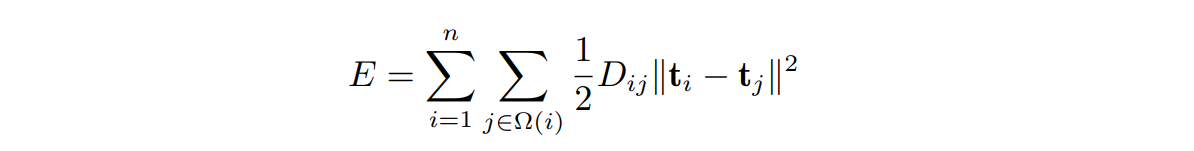

网格每个顶点在参数化后可以表示为相邻顶点的线性组合,组合系数 λij 是连接该顶点的弹簧系数的加权平均,也被称为仿射组合系数
在指定好组合系数之后,该方程变成关于顶点参数化坐标的线性方程组。如果不增加约束条件,那么零解是其平凡解.可以通过对系统施加额外约束从而得到非平凡解
一种约束条件采用固定边界映射,也称为重心坐标映射方法:将开网格边界上的顶点首先映射到指定的凸多边形边界上,那么这些顶点对应的参数化坐标在方程组中变为已知,从而可以求解内部顶点的参数化后的坐标
在弹簧系统中,可以通过设置合适的仿射组合系数来引导平面网格的参数化
- 凸组合,即保证凸多边形的加权平均仍然在凸多边形内部
- 线性重构,即如果网格本身是平面上的网格,组合后的点保持不变
常用的仿射组合系数有三种:

第九章 几何处理
离散微分几何
传统的微分几何是在连续空间中的进行几何分析的,如光滑的参数化曲面,而计算机中的一切量都是离散的,如由连续曲面离散化成的三角网格,离散微分几何就是将二者进行联系的桥梁
对于离散的三角网格而言,在边或顶点的连接处,很多微分量是没有良定义的,因为由三角网格定义出的几何形状只能给出 C0 连续性
局部平均区域
局部平均区域 (local averaging region):从积分的角度描述微分量,计算这个微分量在顶点周围邻域内的积分值,然后假定该微分量在顶点周围邻域内变化很小,可以被近似看成一个定值,于是将积分值除以邻域面积,就可以得到该微分量
顶点邻域的选取方法会直接影响到离散微分量的结果和准确度:
- 若选取的邻域较大,那么得到的微分量在空间上会更为平滑
- 若选取的邻域较小,得到的微分量会更加准确,同时对于网格上的噪声也会更加敏感
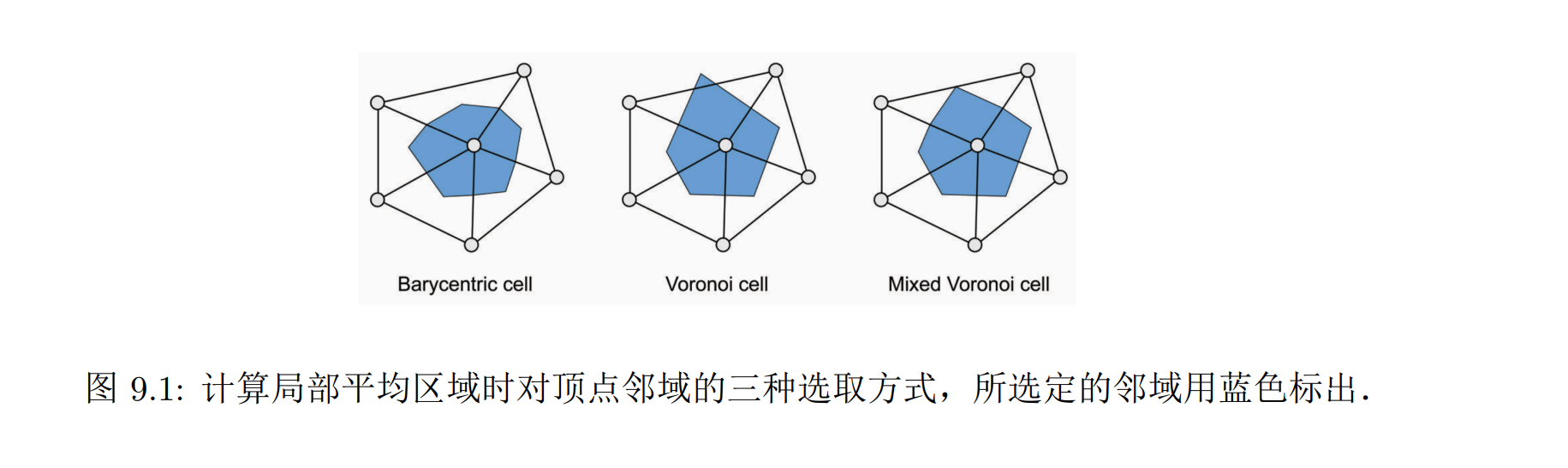
三种定义邻域的方式:
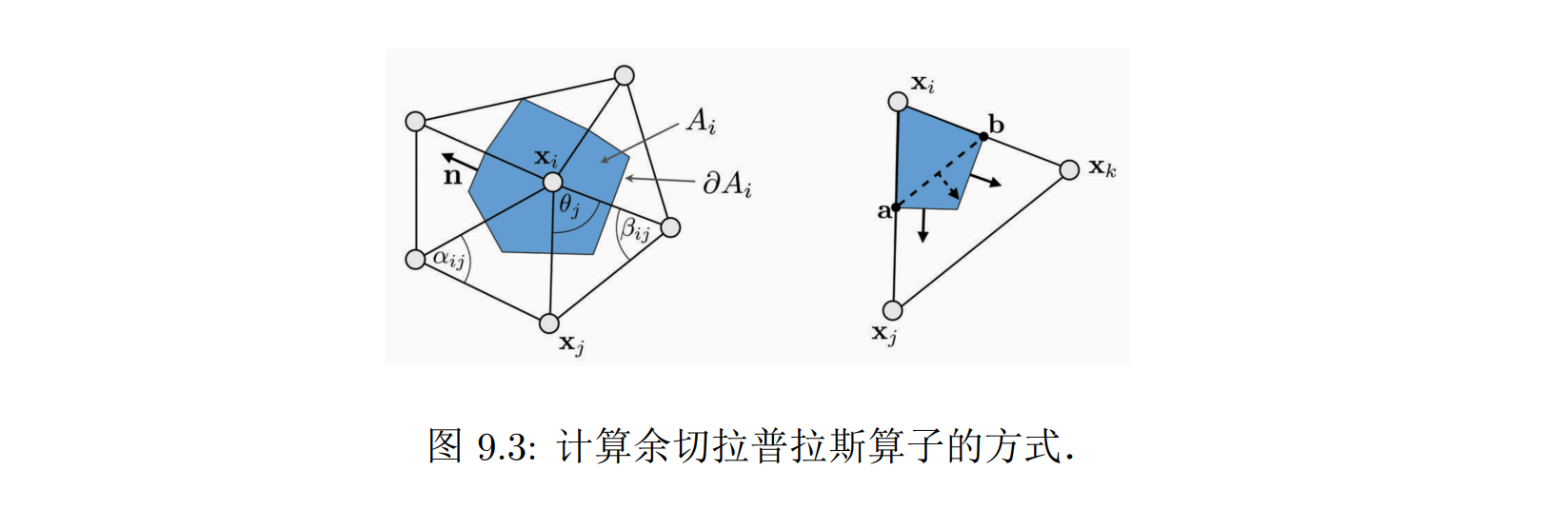
- 重心单元 (barycentric cell),即把三角形的两边的中点和三角形的重心顺次连起来
- 泰森多边形单元 (Voronoi cell),是由每条边的中垂线确定的区域,根据中垂线的性质,每个三角形内,蓝色区域中的点到 x 的距离都会小于另两个顶点,但若顶点周围存在钝角三角形,则蓝色区域会超出三角形
- 混合泰森多边形单元 (mixed Voronoi cell) 是对上一种方法的改进,在出现钝角三角形时,用三条边的中点连线来框选出该三角形内的蓝色区域
法向量
- 三角形内部点的法向量可以唯一定义成三角形所在平面的法向量,而顶点的法向量则可以通过对顶点周围三角形法向量取平均得到:其中,Ω(x) 是与顶点 x 邻接的三角形的集合,αT 及 n(T) 分别是三角形 T 的权重和法向
量
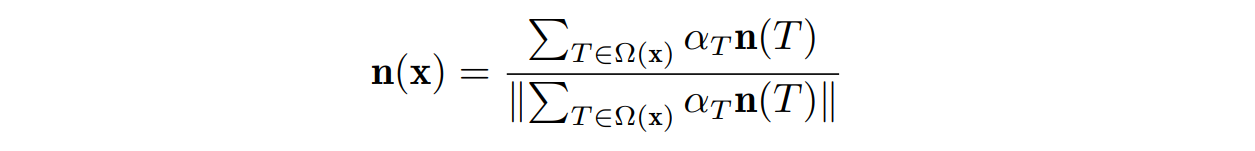
- 对于权重 αT 的选择有很多方式,常见的有以下三种:
- αT = 1.取常数权重是最容易计算的,不过这种取法没有考虑任何三角形的信息,对于不规则的网格会得到一些反常的结果
- αT = area(T).根据三角形面积大小进行加权比常数权重更加合理,且面积大小可以通过两条边叉乘得到,便于计算。但遇到过于不规则的网格时这种做法也不够可靠
- αT = θ(T).根据三角形对应顶点 x 处的角度进行加权可以给出更好的结果,不过这种做法计算起来比较麻烦
梯度
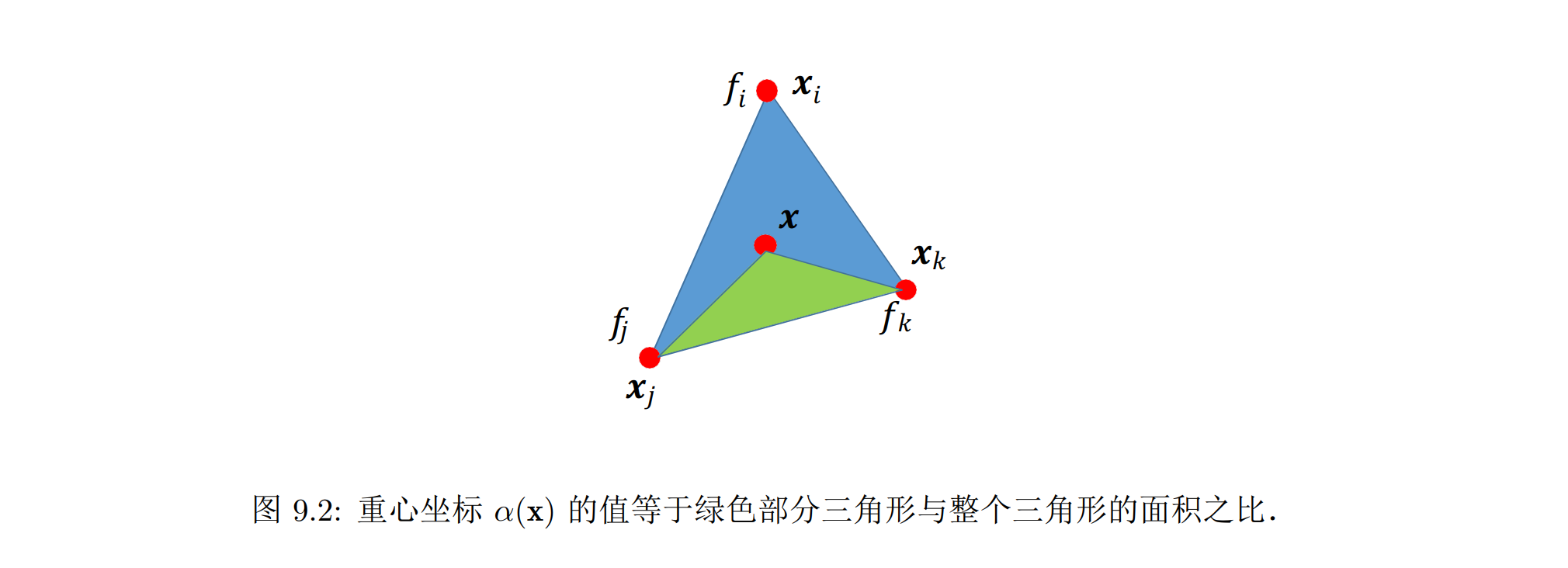
对单个三角形而言,给定三个顶点 xi, xj , xk 上的函数值 fi, fj ,fk,则在三角形内部任一点 x 上的函数值 f(x) 可以根据点 x 的重心坐标 (barycentric coordinate) 进行线性插值得到:f(x) = α(x)fi + β(x)fj + γ(x)fk。其中权重 α, β, γ 是点 x 关于顶点 xi, xj , xk 的重心坐标,且满足 α + β + γ = 1
重心坐标表征的是该点到各顶点的相对位置,一组重心坐标可以唯一地确三角形中的一点
那么函数 f(x) 的导数为:∇xf(x) = fi∇xα + fj∇xβ + fk∇xγ
- 代入重心坐标的表达式可以算得:

离散拉普拉斯算子
拉普拉斯算子被定义为函数梯度的散度:∆f = div∇f
对于标量函数来说,即 ∆f = ∑i(∂²f/∂xi²) ∈R,从定义中可以看出,拉普拉斯算子是一个二阶微分量
拉普拉斯算子应用在标量函数上表达的是函数的趋势,应用在几何表面上刻画的就是几何形状的走向,例如曲面的平均曲率来刻画某处的弯曲程度
记函数 S 是映射到三维空间中的曲面,曲面上某点处的平均曲率为 H,法向量为 n,则有:∆S = −2Hn ∈ R3
在离散情形下,由于三角形面内的梯度是定值,所以拉普拉斯算子恒为 0。因此我们通常从三角形顶点的值出发研究拉普拉斯算子,函数 f(xi) 在顶点 xi处的拉普拉斯算子的一般形式可以写成:ωij 是标量权重,Ω(i) 是顶点 xi 的邻居顶点集合
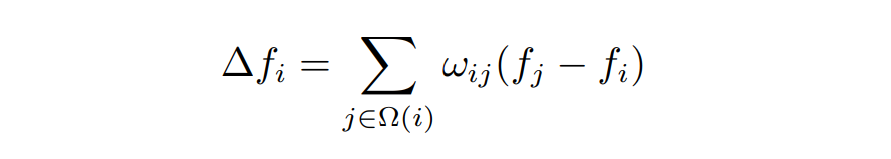
- 不同权重选取方式对应着不同的离散拉普拉斯算子
均匀拉普拉斯
- 均匀拉普拉斯 (uniform Laplacian) 是最简单的一种形式,它将权重取为定值,定义为:其中 Ni 表示邻居顶点的数量
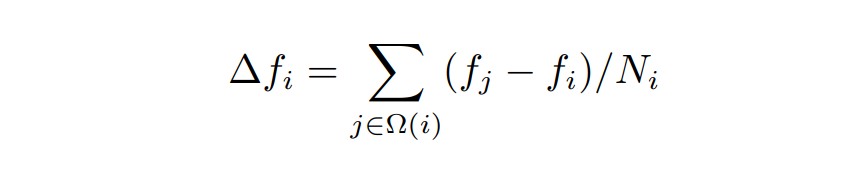
均匀拉普拉斯算子计算的是函数 f 从 xi 到其所有周围顶点 xj 的差的平均值
但实际上它并不是一种恰当的定义方式。我们不能保证一个平面经过三角网格划分后,网格顶点 xi一定处于它所有邻居的中心
余切拉普拉斯
- 通过局部平均区域思想得到的余切拉普拉斯 (cotangent Laplacian):以通过混合有限元 (mixed finite element) 或者有限体积(finite volume) 方法得到

- 当式中两个角度大于 π 时,(cotαij + cotβij ) 会变为负数,这会导致一些三角形发生旋转
网格平滑
网格平滑 (smoothing) 也称为网格降噪 (denoising):降噪一般是指去掉噪音(高频信息)保留整体形状(低频信息)从而获得一个相对光滑的几何模型的过程,比如去掉扫描或者采集数据因为误差或者其他原因导致的噪声
平滑在统计学中指的是通过一个近似函数对输入数据进行较好的拟合,从而保留重要的模式,去掉噪音或者其他不重要的信息
拉普拉斯平滑 (Laplacian smooting)
借助扩散流的数学模型来帮助理解,它常被用来平滑给定的时空信号 f(x, t)。扩散流公式写作:∂f(x, t)/∂t = λ∆f(x, t)
扩散流的过程应用到网格平滑上,也就是将带噪音的顶点坐标理解成杂乱分布的热量。随着扩散过程的进行,热量分布趋于平衡,对应着顶点构成的表面趋于平滑
因此,我们可以通过定义在表面上的拉普拉斯算子,利用扩散流模型,对表面进行平滑
首先,我们需要对公式中的时空信息进行离散化
- 对于空间上的离散化,我们依旧把函数值离散为网格顶点上的值,记 f(t) = (f(v1, t), …, f(vn, t))T,于是对每个顶点有:
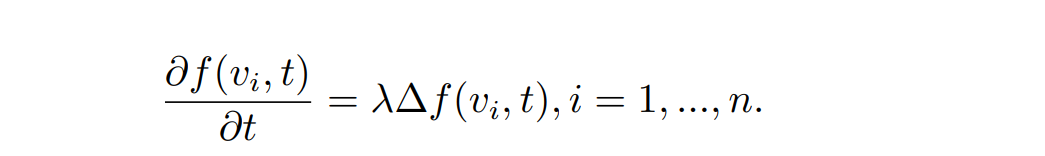
写成矩阵形式为 ∂f(t)/∂t = λLf(t) - 对于时间上的离散化,我们可以采用均匀间隔的时间步长 h 将时间划分为若干段 (0, h, 2h, . . . , t, t+h, t + 2h, . . .),于是通过有限差分可以将偏微分用差值来近似,即:
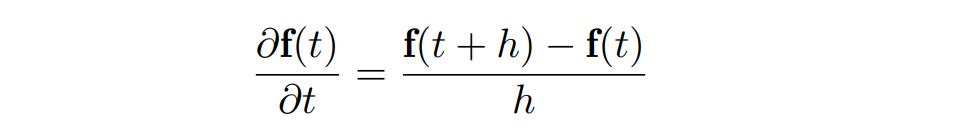
这种差分格式被称为显式欧拉,它的形式可以改写为:
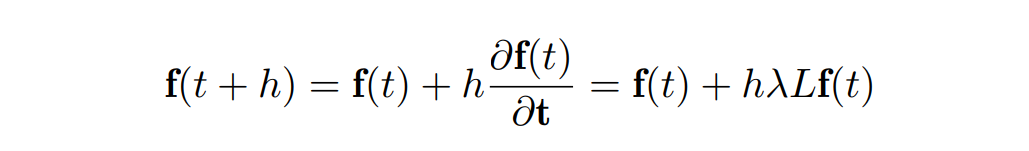
- 对于空间上的离散化,我们依旧把函数值离散为网格顶点上的值,记 f(t) = (f(v1, t), …, f(vn, t))T,于是对每个顶点有:
此式给出了经过时空离散化后函数值的迭代更新方法,每经过一个 h 时间步,用此式更新每个顶点上的函数值,直至达到设定的迭代停止条件
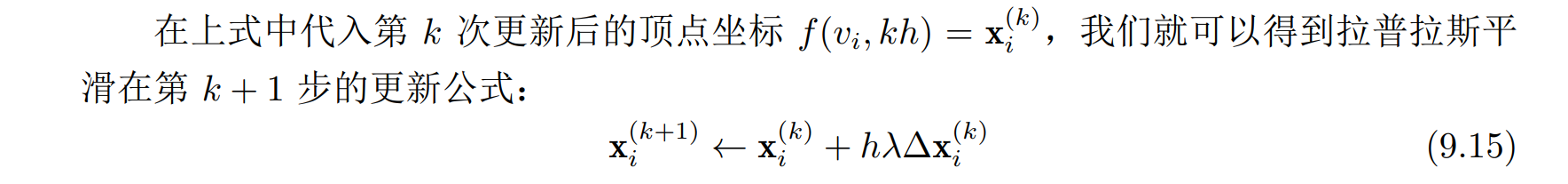
在两种不同的拉普拉斯算子下,可以得到不同的平滑效果。在取余切算子时,由于满足∆x = −2Hn 公式,于是所有顶点将沿着平均曲率定义的方向移动,因此也称为平均曲率流(mean curvature flow)
在取均匀算子的情况下,因为没有考虑面的信息,只考虑了顶点位置,那么平滑不会沿着曲率方向,而是会往重心方向移动,即将每个顶点往相邻顶点的平均位置移动。这个过程等价于某种能量函数最小化,平衡状态下的形状应该是所有边长度相同。这种方式定义的拉普拉斯算子不反映网格形状,可能导致局部几何特征的失真
余切算子能更好地保持几何特征,而均匀算子导致了三角网格切向的松弛
网格简化
网格简化算法可以生成不同细节层次 (Level Of Detail,简称 LoD) 的模型,于是可以在不同情况下选择不同细节层次的模型来渲染
网格简化 (mesh simplification) 的目标是用更少的面片数来表达原有模型,降低模型精度的同时保持模型的整体形状
- 静态简化:化预先计算好一系列不同简化率的模型,在实时运行的程序中可以按照模型离视点 (view point) 的距离选择不同版本的模型进行渲染
- 动态简化:静态简化的延伸,在运行过程中按照需要对模型进行简化,一般使用局部的几何变换来实现,从而生成具有连续的具有不同分辨率的近似模型
简化网格一般可以通过移除顶点或坍缩边来进行,相对来说边坍缩(edge collapsing)算法是更为简单而常用的,它通过删除网格中的边来实现简化的效果
核心:设计一种方法来选出需要被删除的边,并将这条边两端顶点合并成一个点放置在新的位置上
根据不同原则设计出的不同方法直接关系到简化后的模型的质量,不良的处理方法甚至会导致网格模型出现拓扑上的错误
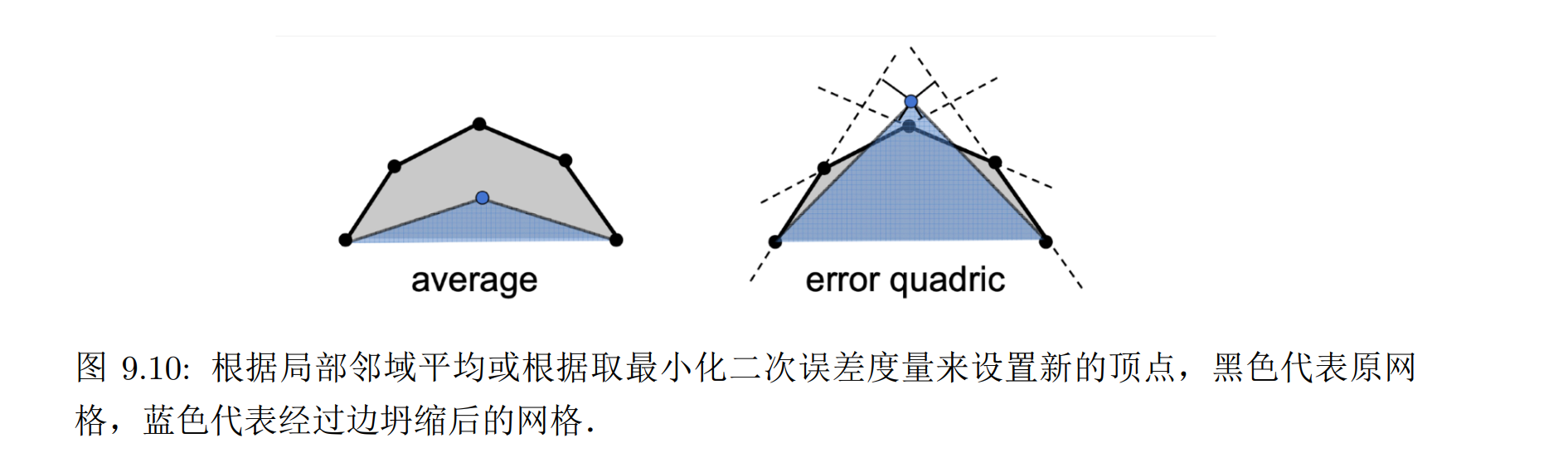
为了衡量坍缩某条边对模型造成的影响,我们需要引入一种误差度量的方式,一种最常用的方式是二次误差度量 (quadratic error metrics)
在删除一条边后,我们需要引入一个新的顶点,通过最小化新的顶点与之前对应的平面的 L2 距离,我们可以得到删除这条边会引入的二次度量误差,于是我们可以选取引入二次度量误差最小的边进行坍缩
使得这条边二次度量误差最小化的顶点,也将被设置为边坍缩后的新顶点
这种设置方式优于取边中点或局部区域平均,可以更好地保留模型的几何特征。利用这种贪心的思想,通过不断的迭代坍缩,我们就能实现对网格的简化
网格编辑
网格编辑 (mesh editing):操纵和修改网格表面的几何形状,同时能够保留原始网格几何细节 (detail preserving) 的操作
对于定义在区域 Ω 上的目标颜色场 g(x, y),泊松图像编辑通过求解下面的优化问题来得到融入后的颜色场 f(x, y):
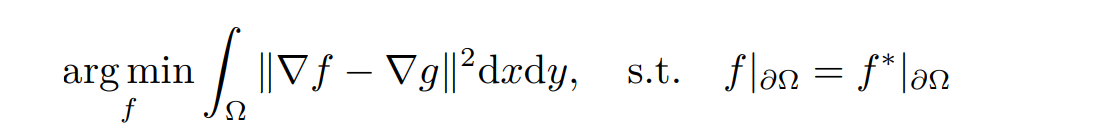
它在保证边界上无缝衔接的同时使得填补后区域的颜色梯度 ∇f 与给定颜色场的梯度 ∇g尽可能接近.拉普拉斯编辑是 ∇g = 0 的一类特殊情况,它完成的是图像补全的任务
类似的思想在三维的应用就是拉普拉斯网格编辑技术.通过尽可能对齐编辑后网格上的拉普拉斯微分坐标来保留细节内容,拉普拉斯微分坐标本质上就是每个网格顶点上关于位置坐标的均匀拉普拉斯算子,记为:
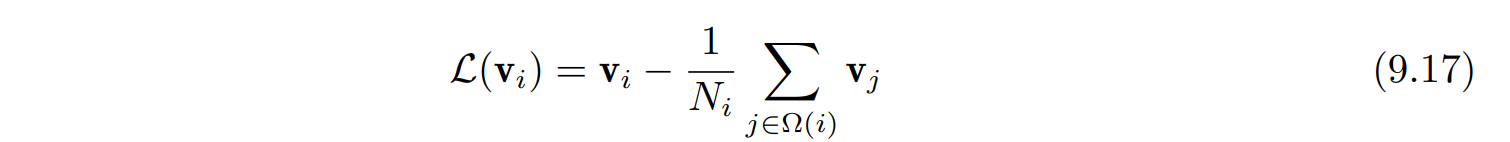
它是一种相对坐标,在给定边界条件的情况下可以与世界空间的位置坐标互相转化
拉普拉斯坐标是网格顶点坐标的线性组合,与点的法向和曲率无关,因此可以被用来描述局部特征
拉普拉斯网格编辑的思路:在交互中指定一些顶点的目标位置后,重建一个既满足这些顶点约束、又尽可能保持局部拉普拉斯微分坐标的网格。
具体来说,设给出的具有 n个顶点的网格模型的顶点坐标为 {v1, . . . , vn} ,首先计算出对应的拉普拉斯坐标:∆i =L(vi), i = 1, . . . , n.而后对需要调整的顶点给出约束:v′j = uj , j ∈ C,其中 C 是受约束点的集合。于是我们可以构造出拉普拉斯网格编辑对应的最优化问题:
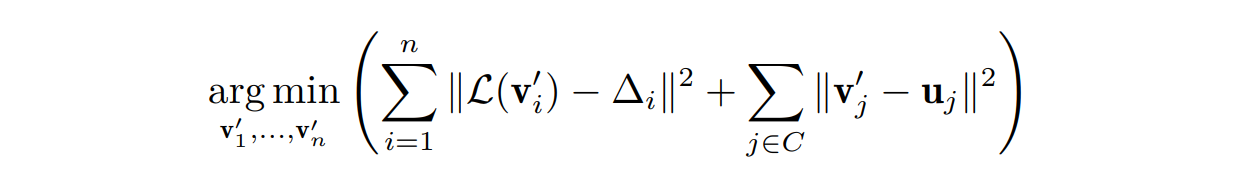
- 利用最小二乘方法求解该优化问题即可得到生成编辑后的网格
第十章 几何变换
二维几何变换
- 基础二维几何变换包括平移、旋转,缩放,反射和剪切变换
平移
对一个点 (x, y) 增加一个偏移量 (dx, dy),将其移动到新的位置 (x′, y′),即实现了平移(translation) 操作:x′ = x + dx, y′ = y + dy
将平移变换表示成矩阵形式,设原始图形为 P,偏移量表示为 D,偏移后的图形为 P′,有P.T = [x,y]、p’.T =[x’,y’]、D.T = [dx,dy]。从而平移可以抽象为 P′ = P + D
平移是移动对象但不改变其形状的刚体变换
线段的平移可以通过移动端点,再重新绘制端点间的部分,多边形移动可以通过移动顶点,再重新进行连线
缩放
缩放 (scaling) 可以用来改变物体的大小,缩放的比例称为缩放系数 (sx, sy):x′ = x · sx, y′ = y · sy
或表示成矩阵形式 P′ = S · P,其中S = {sx,0,0,sy}(2x2)
当 sx = sy 时,缩放后的对象与原对象比例不变,称为一致缩放,不等时则称为差值缩放
0 < 缩放系数 < 1,对象变小,缩放系数 > 1,对象变大
当缩放系数为负数时,会将变换对象进行翻转,特别的,产生镜像的变换称为反射 (reflection) 变换
关于 x 轴反射,关于 y 轴反射,关于原点对称的反射矩阵分别为:
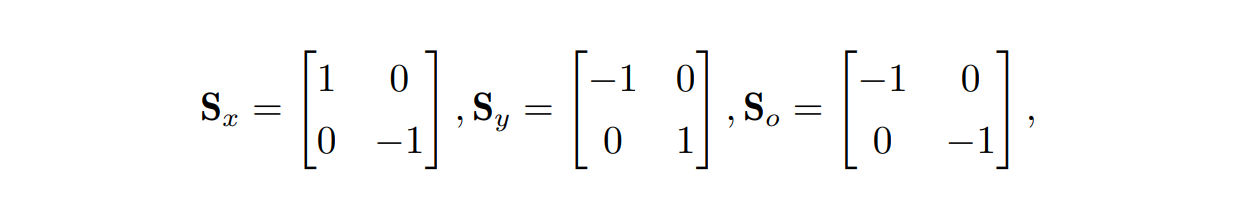
旋转
旋转 (rotation) 变换需要指定旋转轴和旋转角度,将对象的所有顶点绕旋转轴旋转指定角度后,对象完成旋转变换。对二维图形来说,旋转轴通常垂直图形所在平面,投影到平面上成为旋转点
以旋转点为原点为例,点 (x, y) 绕原点逆时针旋转角度 θ 可以表示为:x′ = x cos θ − y sin θ,y′ = x sin θ + y cos θ
用矩阵形式表示 P′ = R · P,其中R = {cos θ,- sin θ,sin θ,cos θ}(2x2)
R 矩阵是一个正交矩阵,满足 RR.T = R.TR = I.但并不是所有的正交矩阵都是旋转矩阵
所有行列式为 1 的正交矩阵都是旋转矩阵,所有特征值为 1 的正交矩阵构成的群称为特殊正交群(Special Orthogonal Group),在二维情况下记为 SO(2)。二维旋转变换与 SO(2) 群里的元素一一对应,旋转角 θ 和旋转矩阵 R 只是 SO(2)群的两种表示方法
所有行列式为 −1 的正交矩阵可以写为旋转矩阵乘以反射矩阵
剪切
剪切 (shear) 是使对象形状发生变化的变换,经过剪切的对象看起来像滑动内部夹层进行的变换,常见的剪切是沿 x 轴和沿 y 轴方向进行剪切
相对于 x 轴的 x 方向剪切变换可表示成下列矩阵:1,α,0,1,这个矩阵不会改变 y 坐标的值
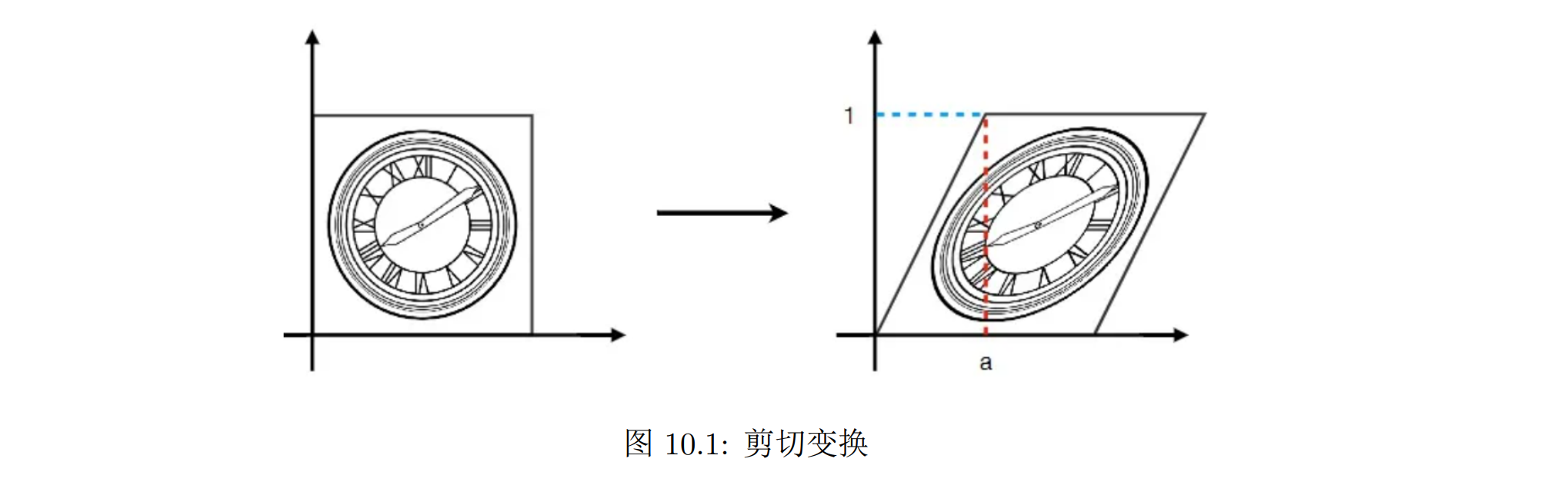
二维的旋转可以分解为两个类似于剪切的变换的复合:分解中的每个变换可以看成缩放变换与剪切变换的复合,这些类似剪切变换都有一个特征,就是会固定一个维度不动,而对另外维度进行缩放与平移
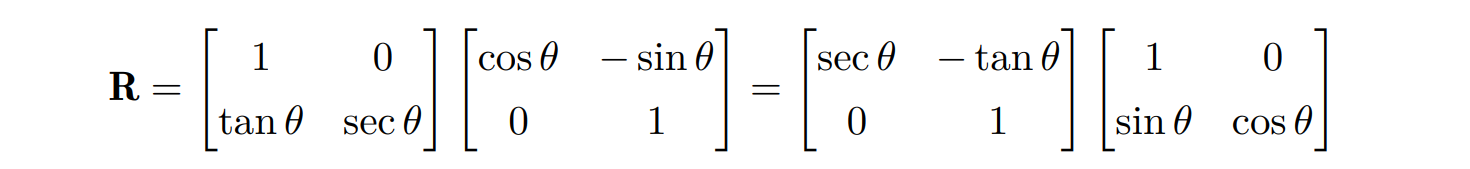
这样分解的目的:提供了图片旋转的快速实现方法,可以逐行绘制像素,就像之前介绍的扫描线算法,并且各行之间是完全独立的,因此可以并行实现
齐次坐标
- 二维空间下的齐次坐标 (homogeneous coordinate),将二维坐标表示 (x, y) 扩充为(xw, yw, w),其中 w 被称为齐次参数,笛卡尔空间和齐次坐标的转换可以表示为
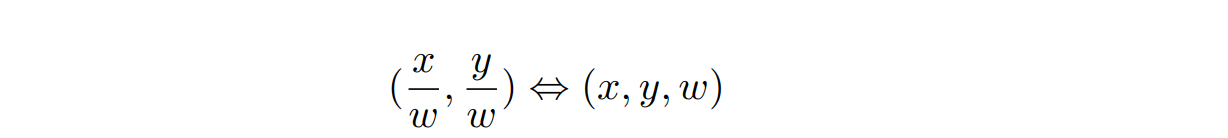
- 齐次坐标的好处:
- 齐次坐标的引入能够描述透视空间的特征:在欧式空间中,同一平面的两条平行线不能相交;在透视空间里面,两条平行线可以相交。齐次坐标具有规模不变性,即对于所有的 (wx, wy, w),它们都对应欧氏空间中同一个点的 (x, y)。从而求解欧氏空间中的平行线相交方程:
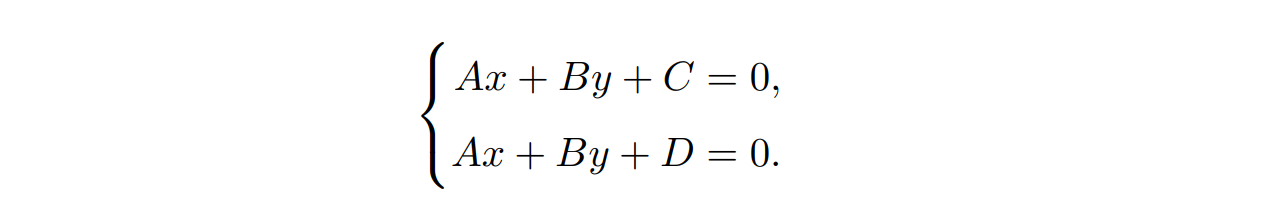
在笛卡尔坐标系中,C ̸= D 意味着方程无解,但如果变换到齐次坐标系下: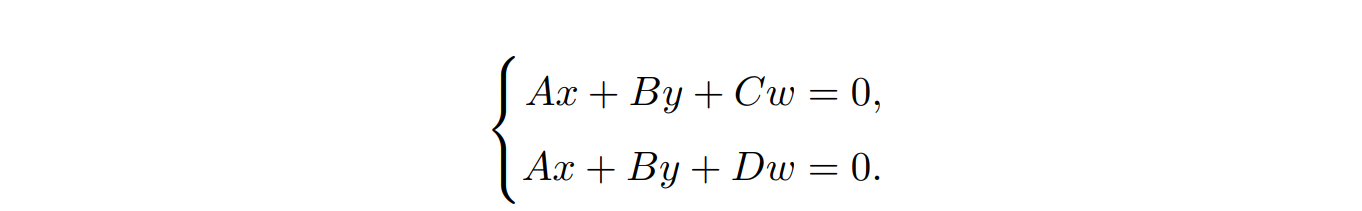
则存在无穷远处的解 (xw, yw, 0) - 齐次坐标可以用来区分点和向量:当 w ̸= 0 时,(x, y, w) 唯一对应笛卡尔坐标系下的点,而当 w = 0 时,(x, y, w) 则可以表示向量
- 齐次坐标很适合表示线性变换:而在齐次坐标下,平移变换矩阵 D(2x1)、旋转矩阵和缩放矩阵(2x2)都能转变成 3 × 3 的矩阵,且不再区分加法和乘法,所有的操作均变成了矩阵乘法
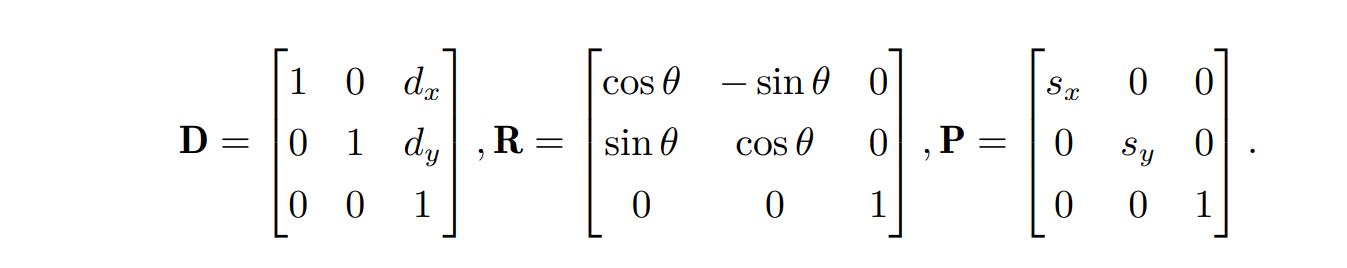
- 齐次坐标的引入能够描述透视空间的特征:在欧式空间中,同一平面的两条平行线不能相交;在透视空间里面,两条平行线可以相交。齐次坐标具有规模不变性,即对于所有的 (wx, wy, w),它们都对应欧氏空间中同一个点的 (x, y)。从而求解欧氏空间中的平行线相交方程:
复合变换
可以将复杂的变换拆分成简单的变换,组合起来即得到复杂变换的变换矩阵
举例来说,“绕特定点 (a, b) 进行旋转 θ 角”可以转变成“平移 (−a, −b)”+“绕原点旋转 θ 角”+“平移 (a, b)”,对应的变换矩阵就是
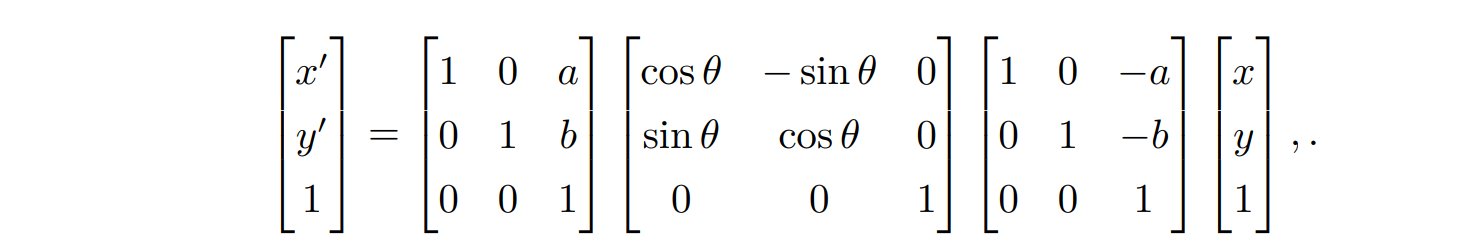
- 注:矩阵乘法满足结合律,但不满足交换律,“先平移后旋转”和“先旋转后平移”对应是完全不同的几何变换
仿射变换
- 如果坐标变换满足如下形式,则称该变换为仿射变换,变换后的坐标是原坐标的线性函数,且参数是常数
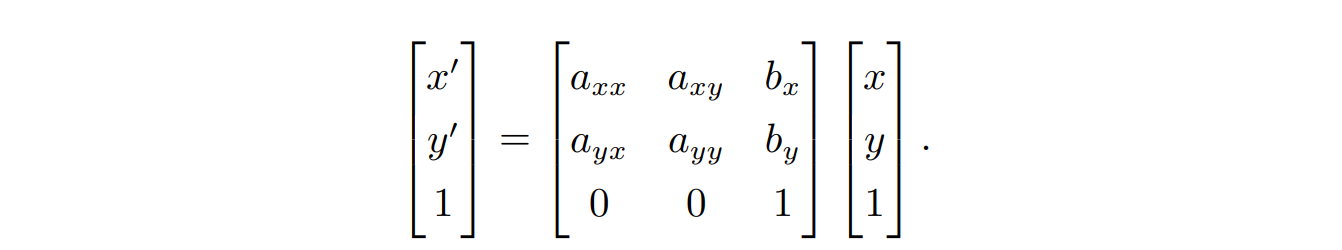
仿射变换有普遍的性质,平行线变换到平行线,有限点变换到有限点
平移、旋转、缩放、反射和剪切是仿射变换的五种特例,任何仿射变换均可以表示成这五种特例的组合
仅包括平移、旋转和反射的仿射变换保持角度和长度以及线条间平行性不变
三维几何变换
- 三维空间的几何变换,在二维的基础上增加了 z 轴,三维空间中的旋转和缩放很容易从二维扩展过来
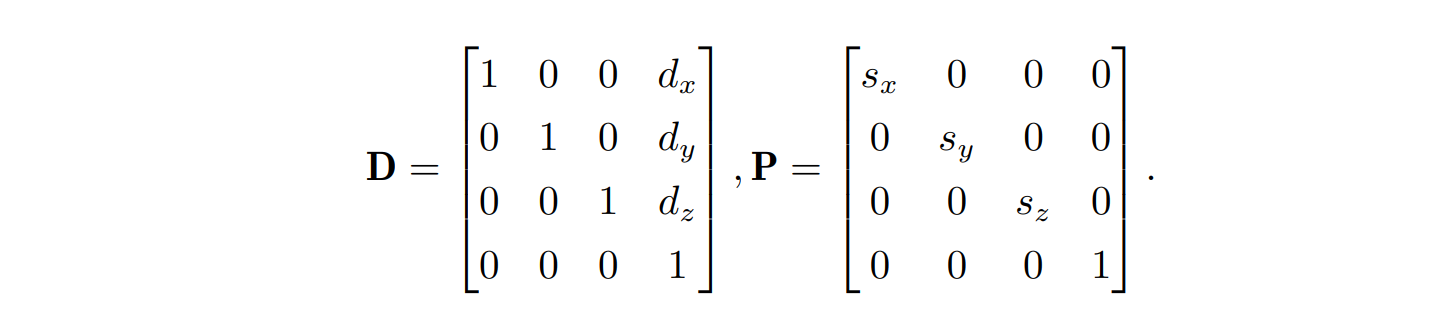
- 三维旋转却要复杂不少,三维空间的旋转可以围绕任意一根轴进行旋转。本节只介绍两种最基础的旋转表示方法,欧拉角和旋转向量
欧拉角
- 欧拉角是用来描述三维空间中刚体的转动角度的三个独立角度。三维旋转包含三个自由度,欧拉角将三个自由度分别给了三个确定的轴,即用绕三个确定轴的旋转来表示任意旋转。以常见的航空领域的用法为例:
- 先绕全局的 Z 轴旋转(偏航角),这时候目标自己的坐标系也发生了旋转
- 再绕自己的 Y 轴旋转(俯仰角)
- 最后绕自己的 X 轴旋转(滚转角)
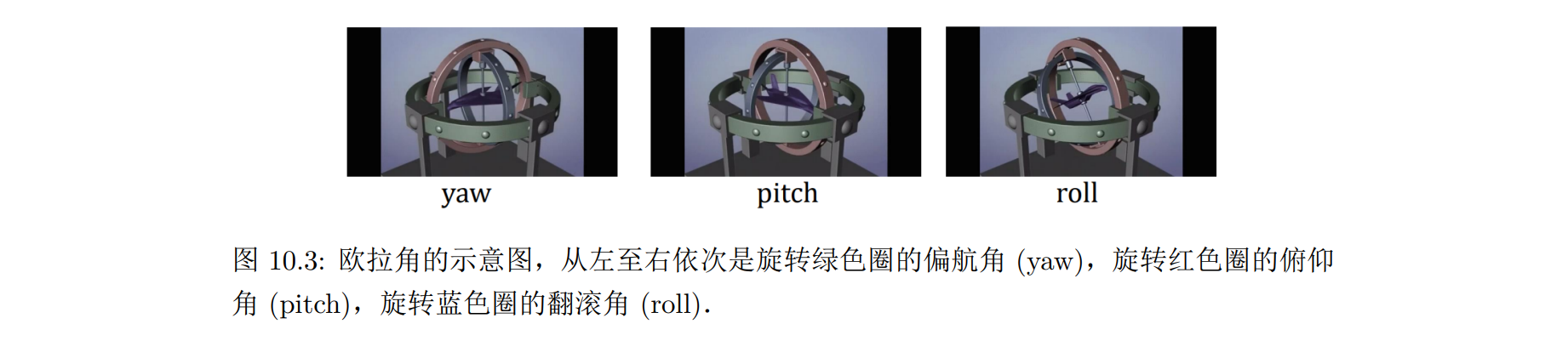
欧拉角的选取有很多种,除了用三个不同的轴,也有用两个轴(如 ZXZ)的表示方法,以及绕固定轴(全局)和运动轴(局部)的区别
结论:三次绕固定轴旋转的最终姿态和以相反顺序三次绕运动轴旋转的最终姿态相同
欧拉角有一个很常见的问题——万向锁(Gimbal Lock):在动态表示(ZYX)下,当俯仰角等于 ±90 度时,第三次旋转和第一次旋转效果等价,丢失了一个表示维度的问题
直观理解万向锁:当俯仰角等于 ±90 度时,局部坐标系下的 X 轴,被旋转到了全局坐标系下的 Z 轴上,与最开始绕 Z 轴旋转也就具有相同的旋转效果
轴角表示法
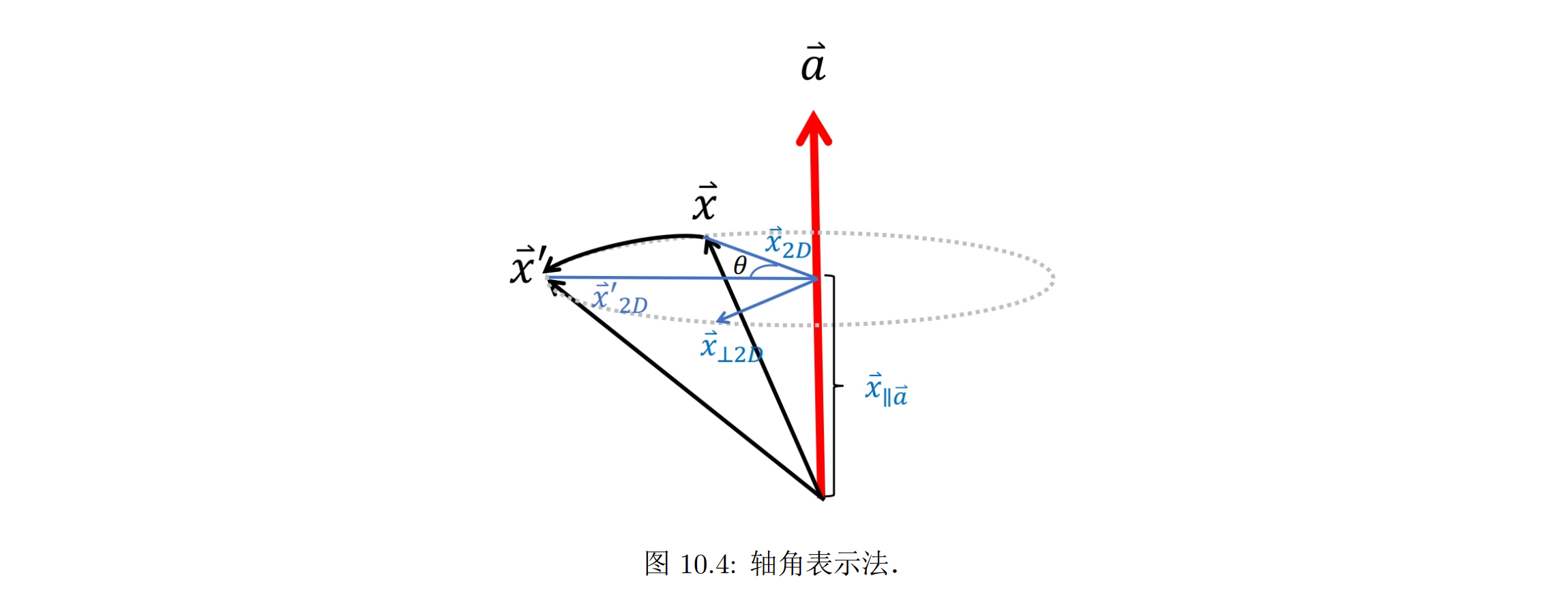
欧拉角的不足:
- 依赖于坐标轴的选定
- 存在万向锁的问题
轴角表示法:假设有一根经过原点的旋转轴 a(如果不经过原点,可以先平移到原点,旋转完再平移回来),我们希望将向量 x 绕旋转角旋转 θ 度(从旋转轴正方向看去,进行逆时针旋转),变换到 x′。对于任意旋转轴,可以用罗德里格斯公式求解旋转矩阵
罗德里格斯公式的推导:采取拆分的思想,将旋转向量 x 拆分成与旋转轴 a 平行的分量 x// 和垂直分量 x2D,其中x// 旋转前后不变,只需要考虑 x2D 的变化:

- 轴角表示法非常直观且紧凑,但有个很大的缺点是很难进行旋转的插值
坐标变换
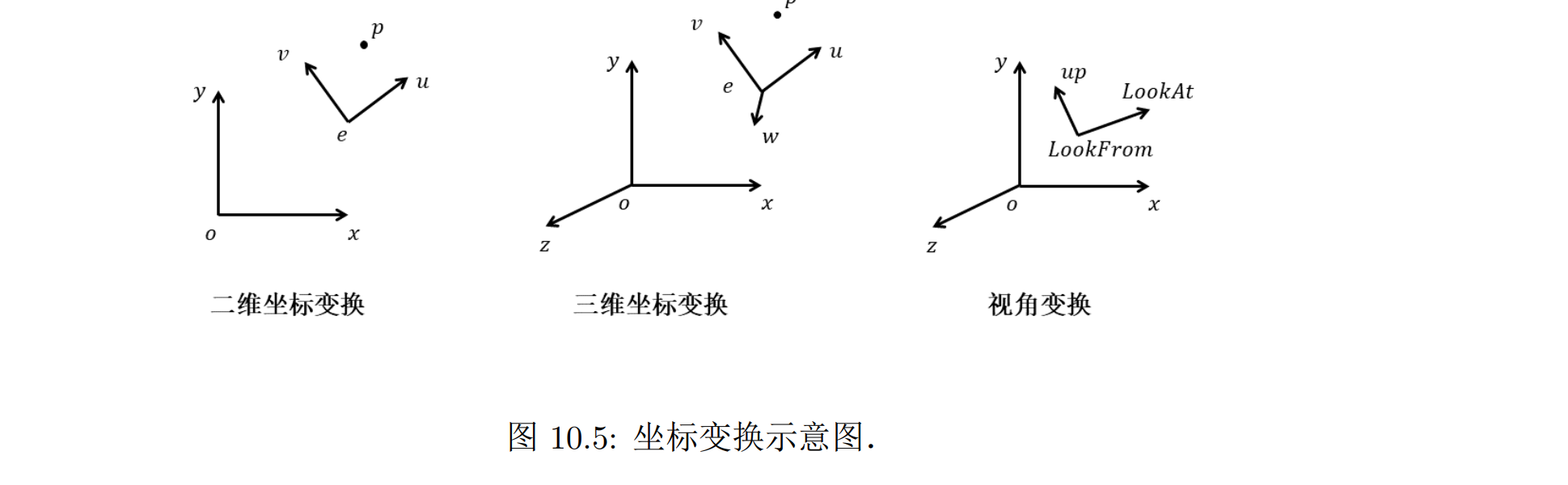
二维坐标系变换
- 点 p 在坐标 uv 和坐标 xy 下的坐标分别为
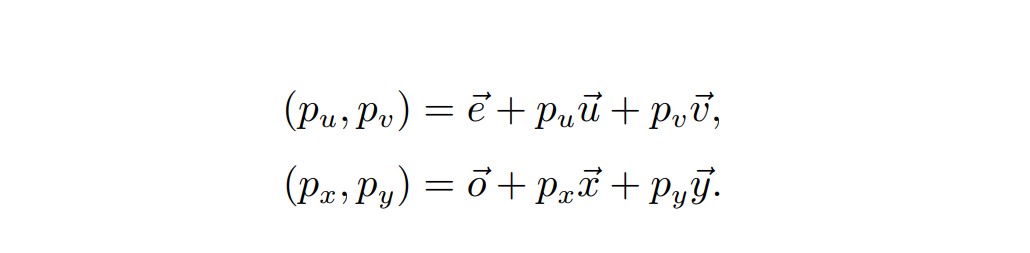
- 这两个坐标表示的是同一个点,从而可以得到从 uv 坐标到 xy 坐标的转换关系,从矩阵形式也可以看出来,二维坐标变换的过程,也可以看作是坐标系的变换,先将当前坐标系进行旋转,再对坐标系进行平移:
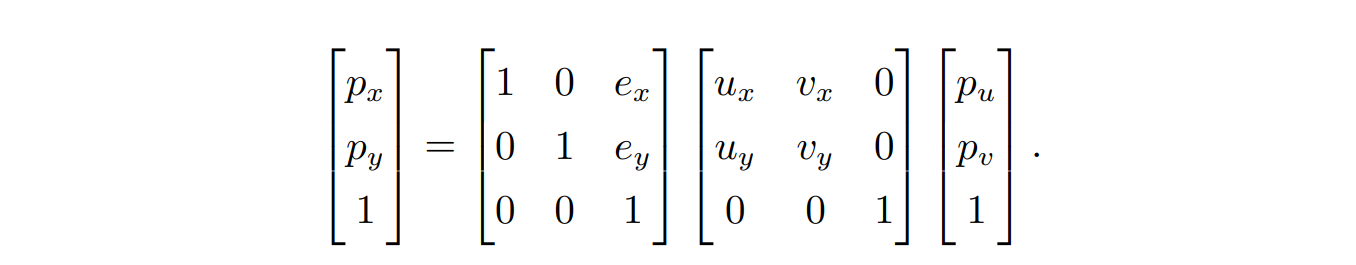
三维坐标变换
- 类比二维坐标变换,三维空间中点的表示 (px, py, pz) 和 (ux, uy, uz),有如下转换矩阵:
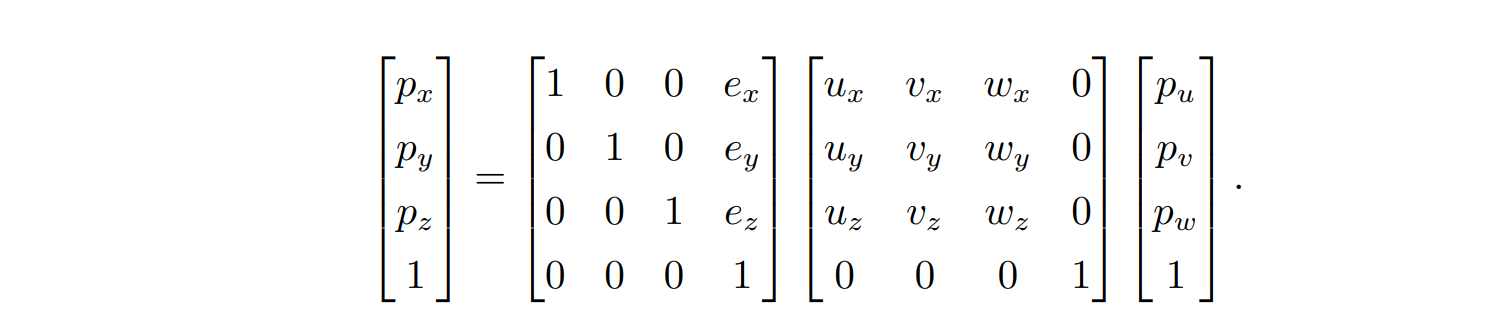
- 视角变换:由三个信息组成:观察点 (LookFrom),观察方向 (LookAt),正上方(up),三个方向唯一确定了观测坐标系。从观测坐标系到全局坐标系可以类似三维坐标变换那样将观测坐标系当作三维坐标系处理,也可以将 LookFrom 平移到原点,再将 LookAt 旋转到 z 方向,最后将 up 旋转到 y 方向
铰接模型
可以只用长方体搭建起一个人体的结构
- 将长方体拉伸成对应部分的形状
- 通过旋转、平移将其移动到合适的位置
人体的各个关节限制了相连部分运动的范围,这样组成的整体称为铰接模型(Articulated Model)
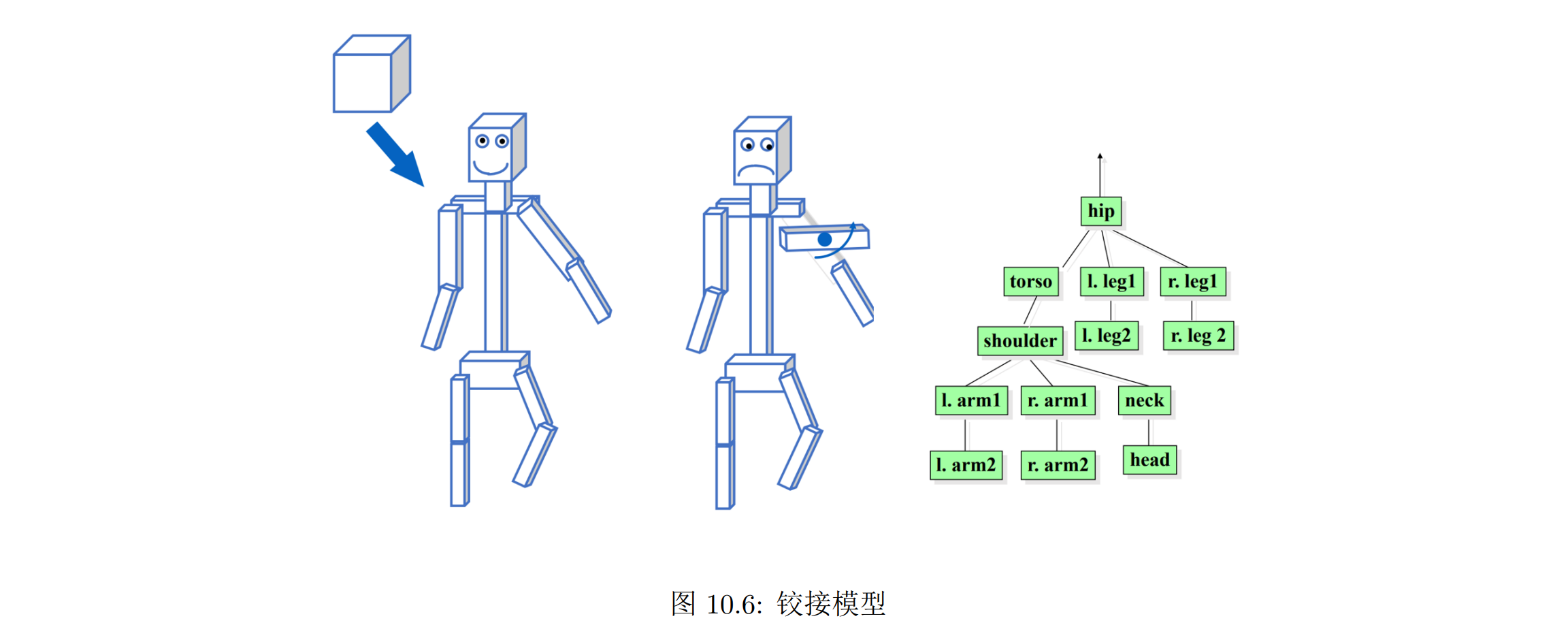
如何在运动过程中手臂关节不会脱臼?我们需要保证手臂是围绕着肩关节旋转.用矩阵形式写出来,手臂相对于肩的坐标变换是 T R,T 表示平移,R 表示旋转。在运动过程中,我们只能改变旋转矩阵,而不能改变平移矩阵,这样就能保证肩关节不会脱臼
因此,对于一条手臂上的多个部分,我们需要按顺序依次对各个部分进行变换.每个部分的变换相对于上一个部分变换之后的坐标进行
因此,假设大臂相对肩关节的坐标变换为 T1R1,小臂相对于大臂的变换为 T2R2,那么小臂相对于肩的变换矩阵就是 T2R2T1R1
如果我们想追踪整个身体的运动,我们实际需要构建出一棵树:
- 树的根节点是身体,根据身体关节的连接关系一直延申到身体末端
- 树上的每个节点都记录了当前节点相对于父节点的平移和旋转
- 当想要计算叶子节点相对于世界坐标的变换矩阵时,我们就需要从根节点开始依次乘上各个节点的变换矩阵
投影变换
- 对于图形学来说,很重要的问题是如何把三维对象,投影到二维平面
三维观察模型
三维观察分两步走
- 第一步是求出世界坐标系下的对象在观察坐标系中的表示
- 第二步是从观察坐标系中将对象投影到投影平面上
观察坐标系由三维空间中的位置 P、观察平面法向量 N,向上向量 V 决定:N 通常是 z 轴正方向,V 是 y 轴正方向,x 轴方向根据左右手坐标系来决定
观察坐标系确定之后,观察对象可以先通过坐标系变换从全局坐标系变换到观察坐标系下,然后在局部坐标系下进行投影
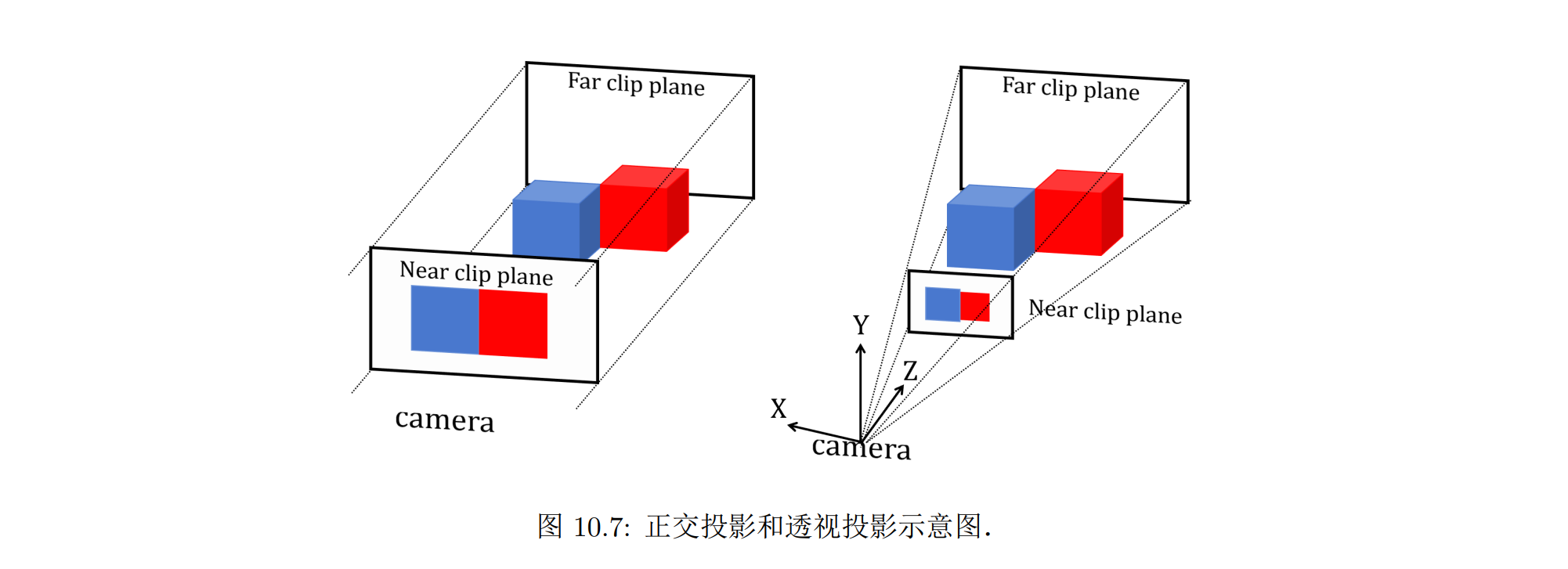
常见的投影方法分为两种:
- 正交投影 (orthographic projection):正交投影坐标位置沿平行线变换到观察平面上,平行投影保持对象的比例关系不变,平行线在平行投影中也是平行的
- 透视投影 (perspectiveprojection):透视投影对象位置沿汇聚到观察平面后一点的直线变换到投影坐标系,透视投影不保持对象的比例关系,但真实感较好,透视投影满足近大远小的效果
正交投影
投影线:连接对象点与投影点的直线
所有投影线平行的投影称为平行投影,正交投影属于平行投影的一种,投影线均与投影平面垂直,投影线不与投影平面垂直的称为斜投影
成像平面大小是有限的,所以对应的三维观察空间也是有限的,这个空间称为正投影观察体
观察体的上下沿和两侧,由与投影平面边框垂直的平面组成,而沿投影平面法向 N,也是 z 轴方向的边缘,通过选取平行于投影平面的两个平面决定,这两个平面称为近裁剪平面 znear 和远裁剪平面 zfar
对于正投影来说,从观察坐标到观察平面的变换很简单,任意一点 (x, y, z) 的投影点就是 (x, y)
为了使观察处理独立于输出设备,图形系统通常将对象描述转换到规范化坐标系,规范化坐标系坐标范围为 [−1, 1](也有 [0, 1]),所以,(x, y, z) 最后需要投影到边长为 2,范围从 (−1, −1, −1) 到 (1, 1, 1) 的立方体内,设观察体在 x 和 y 上的范围分别为 [xmin, xmax] 和 [ymin, ymax],则正交投影的变换矩阵为:
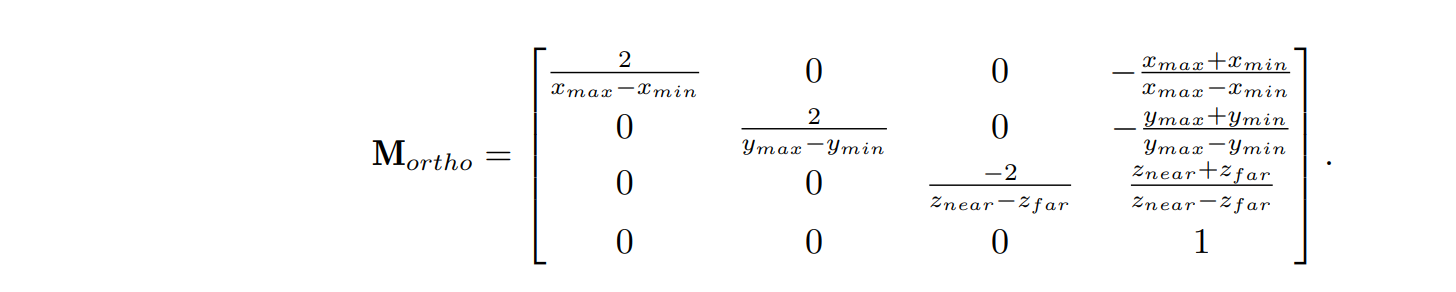
透视投影
正交投影容易生成,且可以保持对象的比例不变,但它的成像缺乏真实感
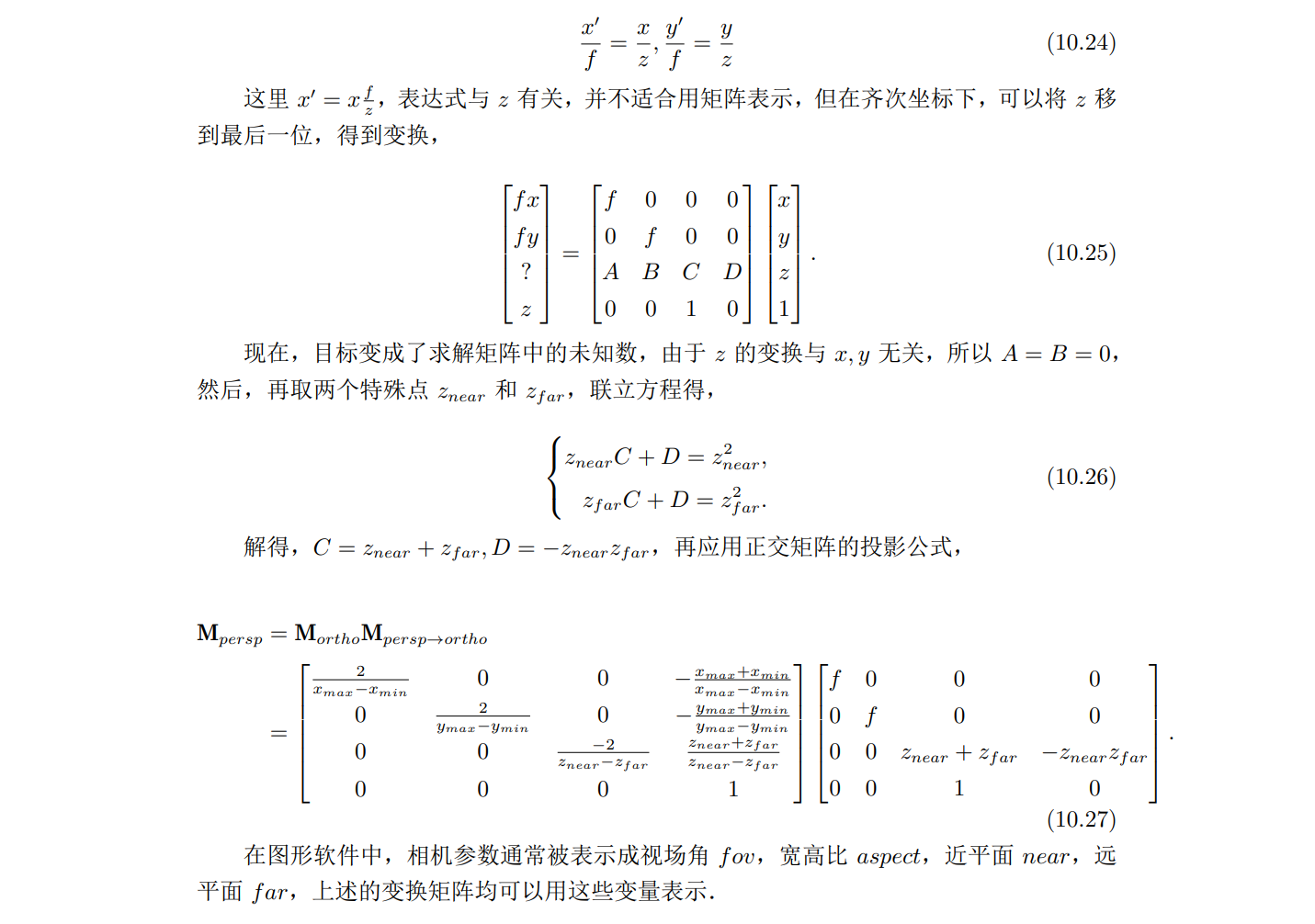
人眼观察和相机拍摄到的图像,通常是符合透视投影的规律:透视投影下,投影线汇聚于投影中心,投影中心到投影平面的距离称为焦距 f
一般相机的成像原理是小孔成像,小孔成像会导致图片倒过来,为了方便,将投影平面放置在拍摄对象同侧
此时的观察体是棱台形状,近剪切面 znear 小,远剪切面 zfar 大.考虑棱台内任意一点 (x, y, z),根据相似原理,它在平面上映射的位置满足:
第十一章 几何重建
- 几何重建是计算机视觉和计算机图形学中的一个经典问题,在计算机视觉和图形学中,几何重建研究如何恢复目标物体(场景)的三维几何形状

点云 (Point Cloud) 是几何重建的一种主要的三维表示方法。形式上来说,点云是指一组三维空间中坐标的集合:{(xi, yi, zi)|i = 1, 2, . . . , N}
在几何重建中,点云数据一般直接来源于 Lidars 和 RGBD 相机,或者从RGB 图像开始,通过一些计算机视觉的算法(例如三角化、束调整和深度学习)生成
点云的注册
在几何重建中,我们往往会对同一个场景采集多组点云数据,最终需要将这些局部点云通过点云注册,对齐成为一个最终的完整点云
最经典的点云注册算法:Iterative Closest Point(ICP)
ICP 流程
通过主成分分析 PCA,初始化一组旋转平移变换 R, t
将这组变换应用于其中一组点云,然后找到其中的每个点在另一组点云中的最近点,如此两两匹配
对于相距太远(点对距离大于中位数的 k 倍)的点对,丢弃
构造误差函数 E =∑|Rpi + t − qi|²
通过奇异值分解 SVD 来最小化误差
重复 2-5 步直到误差小于特定阈值

通过 PCA 初始化
PCA 全称主成分分析 (Principal Component Analysis),可以用来求解数据的“轴”
考虑一组点 p1, …, pn 及其中心坐标 c,构造矩阵 P3×n,使其第 i 列为 pi − c,构造协方差矩阵 M = P × PT,M 的特征向量即代表了数据的“主成分”。对于二维数据,M 的两个特征向量表示数据的两条轴线:
- 对应最大特征值的那个特征向量表示,数据在这个方向上的分布最分散(数值变化最大)
- 对应最小特征值的那个特征向量表示,数据在这个方向上的分布最集中(数值变化最小)
由于这些轴都是正交的,因此我们可以通过分别对两组点云进行主成分分析,然后寻找一个变换来对齐它们的这些轴线,即能得到一组粗略的初始化变换
具体地,对于两组点云 S, T,它们的中心分别是 cS, cT,首先我们将点云 S 平移 cT −cS,然后找到一个旋转矩阵 R′ 使得两组点云的轴分别对齐,则最终得到的变换就是:R = R′, t = cT − R′ × cS。即,对于 S 中的每个点 pi,我们都可以通过应用这个变换得到对齐后的位置:p′i = R × pi + t = cT + R × (pi − cS)
通过 SVD 最小化误差
当已经找到了一系列的点对 (pi, qi) 时(其中 pi 来自点云 S,qi 来自点云 T),可以通过SVD分解来找到更好的R,T来最小化误差
构造矩阵 P,使得其第 i 列为 pi − cS。构造矩阵 Q,使得其第 i 列为 qi − cT。然后构造协方差矩阵:M = P × Q.T。计算 SVD:计算 SVD:M = U × Σ × V.T。则旋转矩阵就是:R = V × U.T。最终的变换为:R = V × U.T, t = cT − R × cS
点云的表面重建
有时点云会具有一些额外信息,例如每个点的法向量和颜色
点云的缺陷
- 即使一个并不够精致的点云模型也将占用很大的存储空间
- 数以万计的三维点也给编辑调整三维模型带来了巨大的困难
- 随着我们将模型放大,点云的渲染质量将会迅速下降:点会变得稀疏,因而在物体表面露出孔隙
点云通常经过表面重建 (Surface Reconstruction) 的方法转化为网格 (Mesh) 的形式来表示。有时点云的表面重建也称作网格化 (Meshing)
网络化的两种方法:
- 德劳内三角剖分 (Delaunay Triangulation)
- 泊松表面重建 (Poisson Surface Reconstruction)
德劳内三角剖分
三角剖分 (Triangulation):将点云转化为三角形网格 (Triangle Mesh)的过程
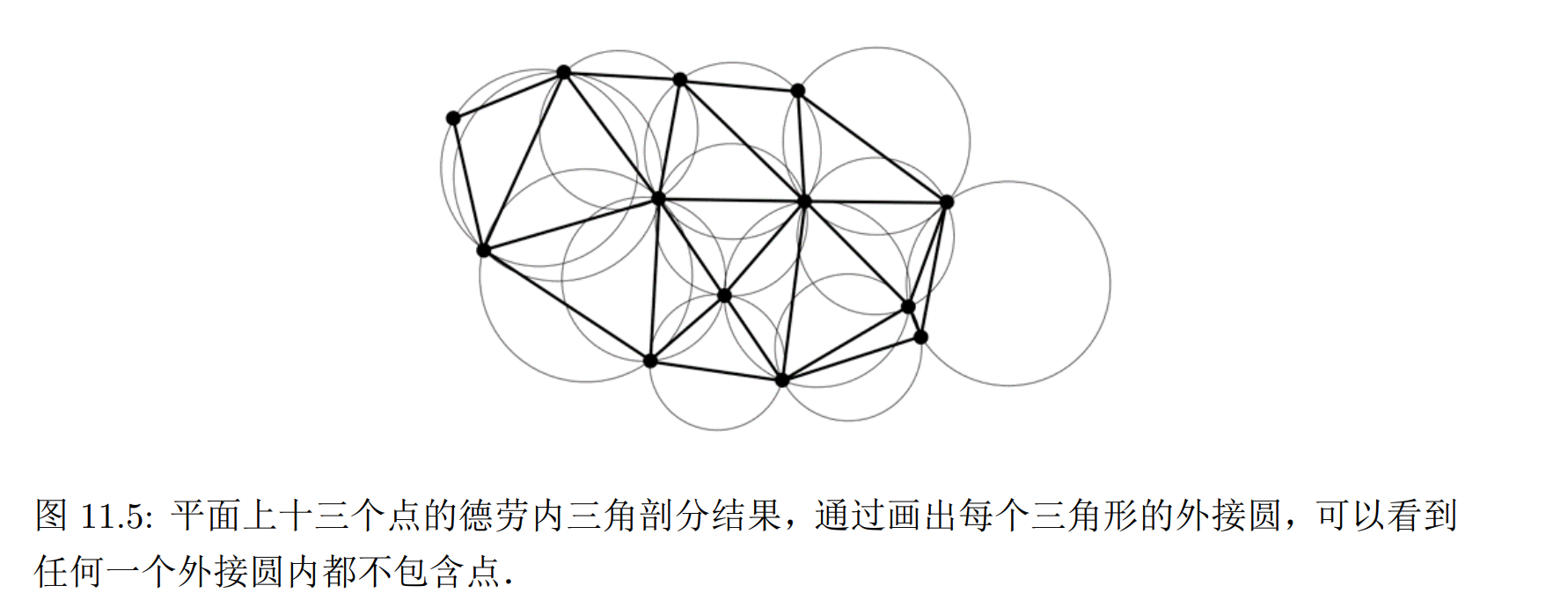
直观的评判三角剖分质量的想法:尽量避免生成过于狭长的三角形。德劳内三角剖分就适用于此,它能够找到一种方法,最大化所有三角形中最小的角
严格意义上来说,德劳内三角剖分并不是一种算法,而是指一类满足了特定条件的三角剖分。条件是:生成结果中,任何三角形的外接圆内,都不包含任何点,这样的三角剖分最大化了“所有三角形中最小的内角”
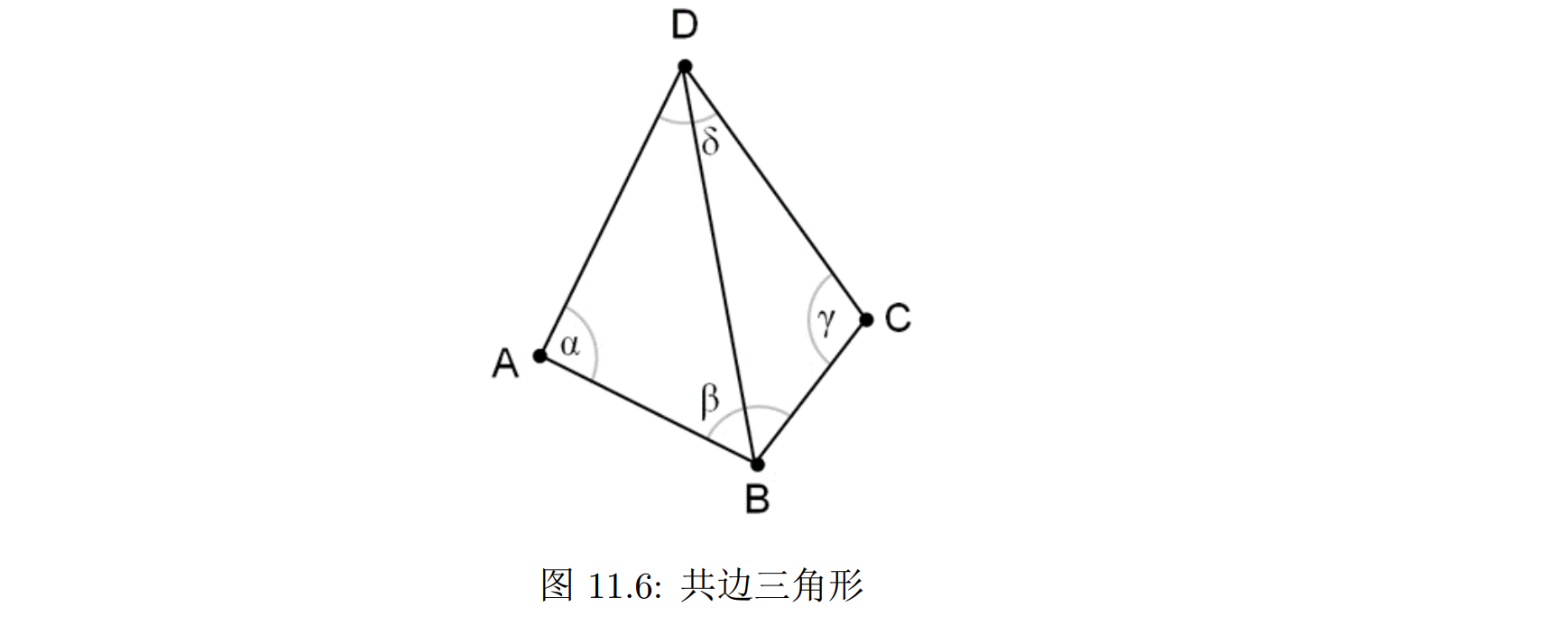
根据德劳内三角剖分的性质,结合三角形外接圆的性质,我们很容易可以得出如下推论:
- 任何一对存在共用边的三角形,必须满足 α + γ < 180 deg,否则就不满足德劳内三角剖分的性质
- 为了恢复这种性质,我们只需要把 BD 之间的边删去,加上 AC 之间的边
这种“翻转”的思路就产生了一个非常简单的算法:
- 构造任意三角剖分,然后检查共边三角形
- 如果不满足性质,就进行翻转,重新连接边
- 重复检查其他三角形对,直到所有三角形对都满足性质
这种最简单的算法并不高效,可能需要检查 Ω(n²) 次,改进:
- 改为增量式进行:每次向当前集合中添加一个点并连接一些边组成三角形,随后检查受到影响的周围的三角形是否满足德劳内性质,并对不满足性质的三角形进行翻转。这样的算法仍然需要检查 O(n²) 次
- 采用分治算法:在这种算法中,我们每次递归地画一条线,将点集分成两个子集.为每一个子集递归地进行三角剖分,然后沿分割线合并这两组.利用一些巧妙的技巧,合并操作可以在 O(n)时间内完成。总时间Ω(nlogn)
泊松表面重建
德劳内三角剖分的问题:当输入的点云数据中包含噪声,或者含有一些错误的点集时,由于三角剖分必然会构造以噪点和错误点为顶点的三角形,这将不可避免地导致视觉上异常的结果
泊松表面重建则并不直接构造三角网格,而是首先通过构建符号距离函数 (Signed Distance Function) 这一隐式表示,然后再通过行进立方体 (Marching Cubes) 算法,从 SDF中提取出三角网格
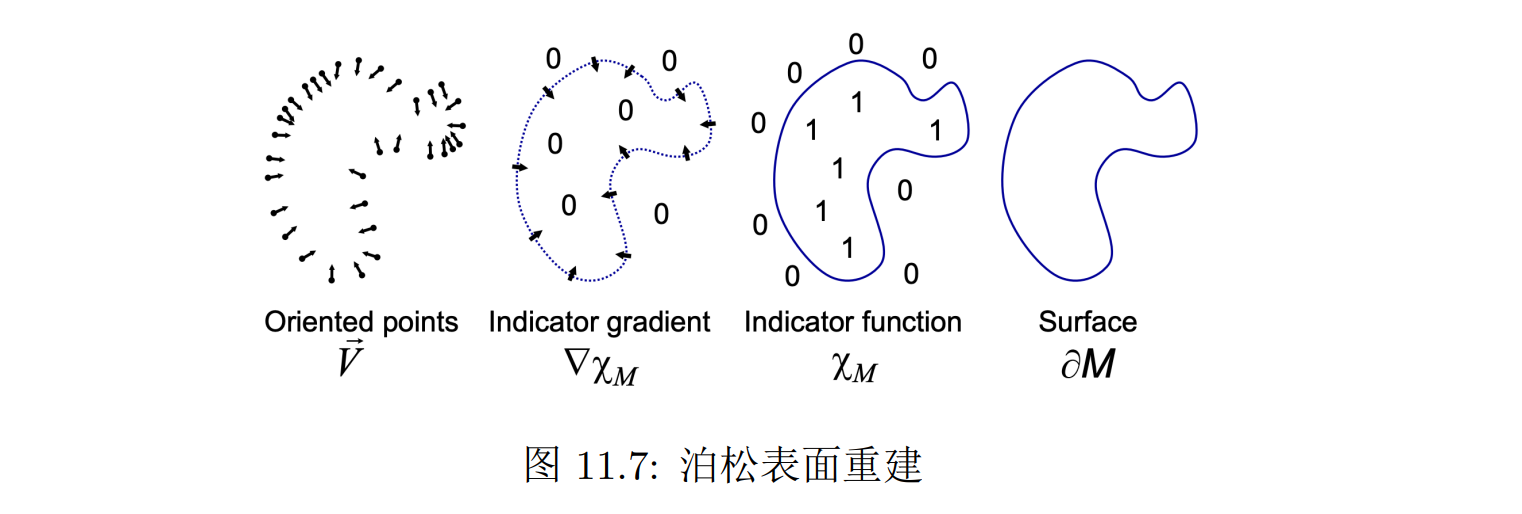
泊松表面重建基于这样一个观察:对于一个空间中的实体 M,如果我们定义一个指示函数 χM 来标识其表面 ∂M,内部的点都具有 1 的函数值,外部的点都具有 0 的函数值,那么该指示函数的梯度场 ∇χM 就只在 ∂M 上具有非零梯度。表面上某一点梯度的方向与该点的法向量恰好反向,因此一个带有法向量的点云 V 可以被看作是指示函数梯度场在边界上的一个采样
因此,当我们可以通过 V 估计出指示函数的梯度场时,问题就转化为如何从一个函数的梯度场恢复出原函数,即从下式中估计 χM:∇χM = V
等式右端的向量场不一定可积(例如有可能并不是无旋的),因此我们无法找到一个精确解,而需要将上式通过泊松方程转化为可以估计最小二乘解的形式:∇χM = V ⇔ ∆χM = ∇ · V
泊松表面重建依赖带有法向量信息的点云数据作为输入。算法通过八叉树 (Octree) 组织这些带法向量信息的点并在八叉树节点上定义一系列基函数,通过求解上述泊松方程得到基函数之间组合的系数,从而最终拟合出指示函数
由于使用了平滑滤波器来进行近似求解,得到的指示函数在表面附近具有类似符号距离函数 (SDF) 的性质,因此通过 Marching Cubes 算法可以从等值面中提取出三角网格,就得到了最终的网格表示
行进立方体算法
- 行进立方体算法,即 Marching Cubes 算法,是一种从符号距离函数来重建表面网格的方法:
- 将空间划分为固定大小的立方体体素
- 根据每个顶点的 SDF 值,确定这个顶点在对象的内部还是外部
- 对于每个体素立方体的八个顶点的 SDF 值正负性,我们将其编码成 2^8 = 256 种情形并用一个 8-bit 二进制索引表示。索引 (Vertex bit mask) 的每一位为 0或 1 分别表示该顶点的 SDF 值小于 0 和大于等于 0。全部 256 个索引构成了 256 种拓扑关系,并可以根据对称性简化为 15 种。这 15 种拓扑关系通过旋转平移等对称性操作就可以覆盖全部 256 种情形
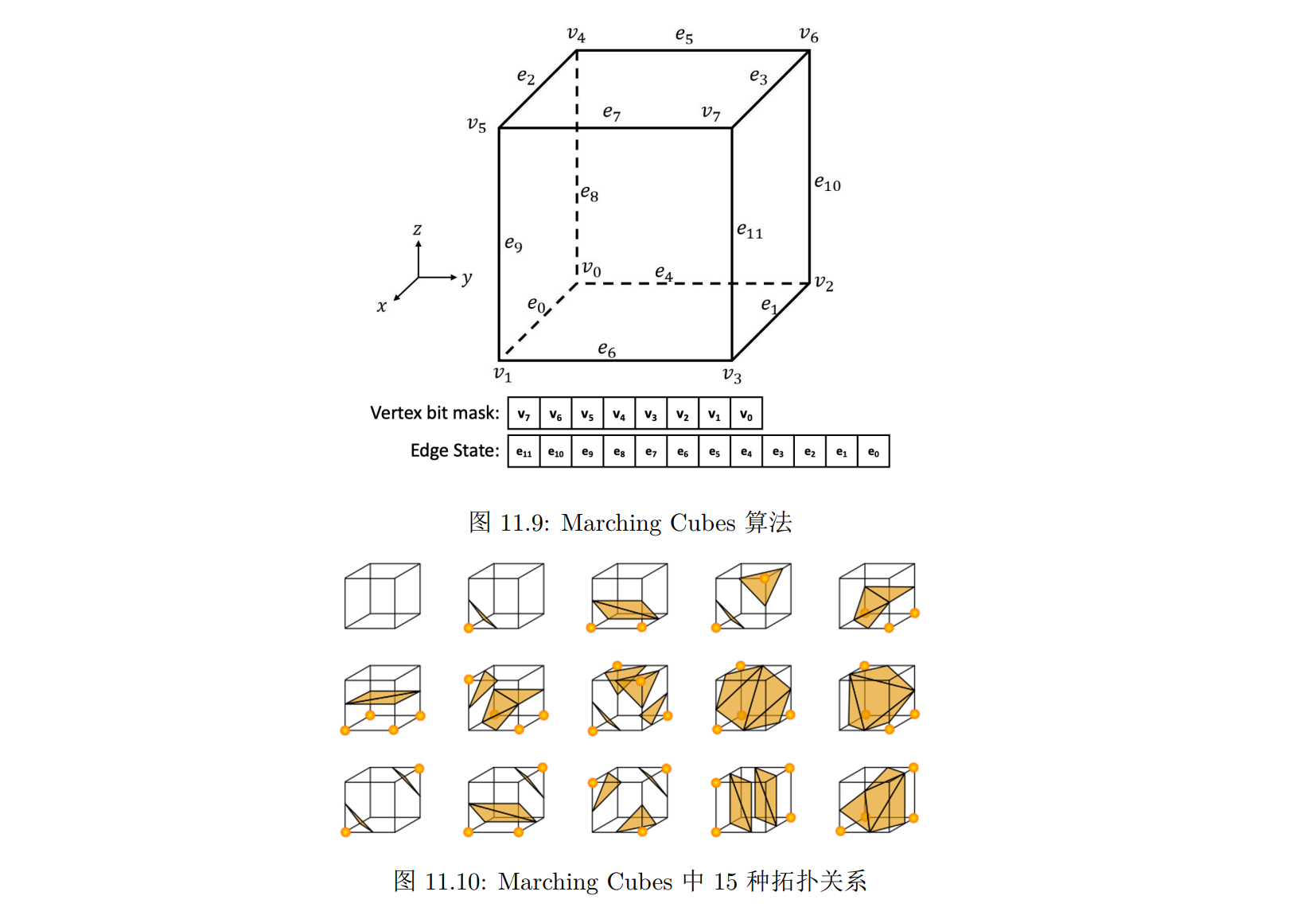
- 算法维护了两个查询表:
- 第一个表根据顶点编码成的索引查询关于边状态的编码 (EdgeState),这是一个 12-bit 的二进制串,其中每一位为 0 或 1 分别表示该边与等值面相交和不相交。根据这些信息可以在立方体的边上生成最终需要的网格顶点。例如边的两个端点分别具有 p1, p2 的位置属性和 v1, v2 的 SDF 值时,通过下式估计等值面(假设等值面处 SDF 值为 v∗)与边的交点,生成所需的顶点网格:
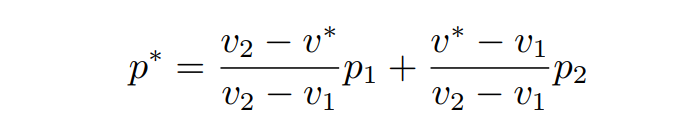
- 第二个查询表包含关于这些生成的网格顶点之间如何连接的信息;根据每个体素的拓扑关系,可以在表中查询等值面与边交点的连接方式,根据查表得到的连接方式连接对应的边,就得到了面片
- 第一个表根据顶点编码成的索引查询关于边状态的编码 (EdgeState),这是一个 12-bit 的二进制串,其中每一位为 0 或 1 分别表示该边与等值面相交和不相交。根据这些信息可以在立方体的边上生成最终需要的网格顶点。例如边的两个端点分别具有 p1, p2 的位置属性和 v1, v2 的 SDF 值时,通过下式估计等值面(假设等值面处 SDF 值为 v∗)与边的交点,生成所需的顶点网格:
- 最后,为每个等值面与边的交点确定法向量,法向量为边的两个顶点法向量按照同样方式进行插值的结果;而体素顶点的法向量,则由 SDF 的梯度确定:通过在 x, y, z 三个方向上计算相邻顶点 SDF 值的差,可以估计在 x, y, z 三个方向上分别的梯度,将它们组合后归一化,就得到了顶点的法向量
- 算法最终输出顶点的位置和法向量,以及组成顶点的网格
点云的模型拟合
点云的模型拟合是从给定的点云中提取出平面或球体、圆柱体等几何基元的过程
几乎所有的几何形状都可以用一个确定的方程来描述它:
- 对于实体:F(x, y, z) ≥ 0
- 对于表面:F(x, y, z) = 0
形式化地定义几何拟合问题(以表面为例):对于给定的点云 P ={(xi, yi, zi)|i = 1, 2, . . . , N} 和给定的形状 F,找到一组 P 的子集 P′ ⊂ P,使得 ∀(x, y, z) ∈P′, F(x, y, z) = 0
目标:定义一个误差函数,然后求解一组点云的子集,使得误差最小化
平面的拟合
输入的点云也基本在同一个平面上,即不存在任何噪点、错误点和无关点.给出三维空间中平面的方程:Ax + By + Cz + D = 0。需要求解 A, B, C, D
对于点云中的某个点 (xi, yi, zi),我们定义误差:Li = (Axi + Byi + Czi + D)²。则总误差:

分解得到的矩阵 V 最后一列即为所求的 M,它将使误差 L 最小化
实际中遇到的问题远比我们刚才遇到的更加复杂,给定的点集中可能不全是待求平面上的点,而有很大一部分其他点集。这就使得刚才使用的最小二乘拟合失效了
随机抽样一致性算法
RANSAC 算法基于这样的一个思想:
- 假设我们希望估计刚才的点云中墙面的位置,而待求墙面上的点,已知其数量至少占整个点云的 30%,而且点云中不存在拥有更多点的平面
- 现在我们每次随机地挑选点云中的三个点(三个点就能确定一个平面),然后估算平面的位置,并且观察整个点云是否至少有 40% 的点落在这个平面上(如果满足,说明我们找到了墙面)
- 只要我们尝试足够多次,总存在某一次随机挑选的三个点,恰好都在墙面上;而且我们发现,至少有 30% 的点落在其上。这样一来我们就确定,找到了墙面的位置
- 从上述过程可以看出,即使存在大量(70%)的无关点,也仍然能够利用随机抽样的方式,来对点云进行几何拟合
RANSAC 算法的流程:
- 随机选择一个用于估算的最小子集(对于估计平面来说,该子集包含 3 个点)
- 用这个子集估算待求的参数
- 用估算的参数测试整个数据集,将误差在一定范围内的数据点作为“内点”(inliers)
- 如果内点的数量超过一定比例,就以全部内点为输入,使用最小二乘法重新估计一组更精确的待求参数
- 重复 1-4 步若干次,最后将“用最多内点估计出的参数”作为最终结果
RANSAC 算法具有鲁棒性好、效率高的特点(不难看出它可以并行化执行)


