Autoencoders

Basics

What is autoencoder?

autoencoder 是一种前馈神经网络，其功能是接收输入x并预测x
存在 Trivial (short-cut) solutions：神经网络可以学会恒等映射 𝑥 = 𝑓(𝑥)，即输入为x，经过中间的神经网络后，输出也为x

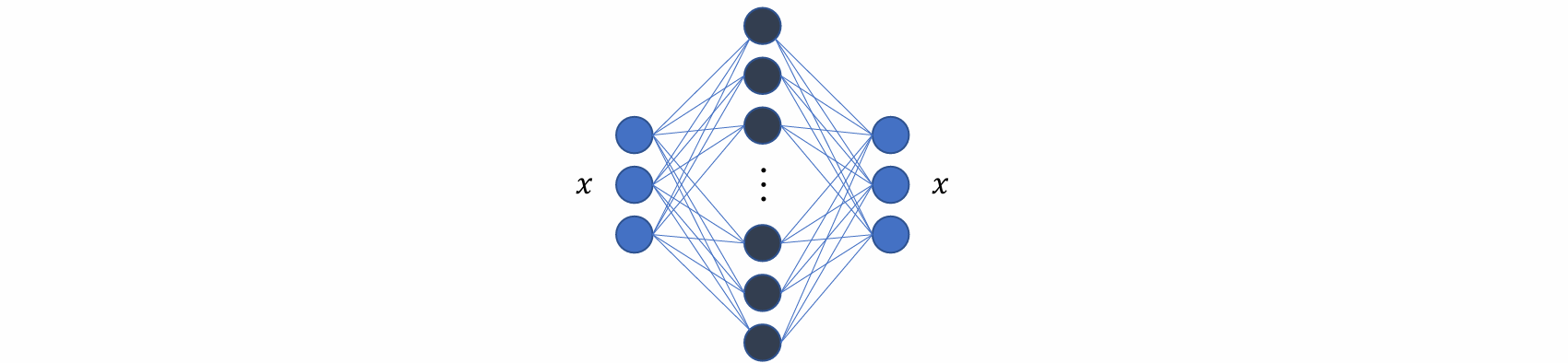
Bottleneck architecture：

使用bottle neck结构：防止过拟合
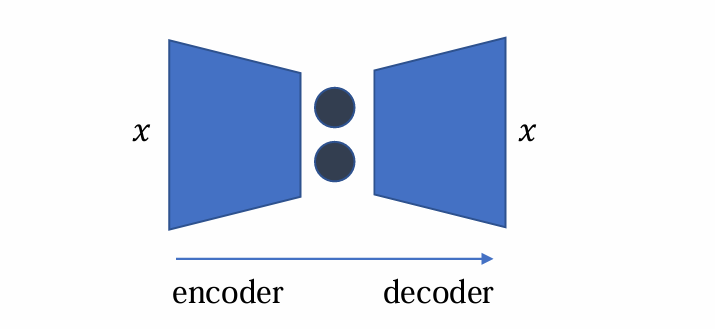
可以分为encoder(编码、降维、提取特征)和decoder(解码、复原重构x)

Why autoencoder?

将高维数据映射至二维空间以实现可视化
数据压缩（降低通信成本）
无监督学习（预训练），通过加入扰动再去噪
生成模型，生成image

The simplest autoencoder(线性autoencoder)

最简结构的autoencoder包含单个具有linear activations的hidden layer
encoder通过线性投影到更小的空间，而decoder则通过线性投影还原到原来的维度，均为线性变化

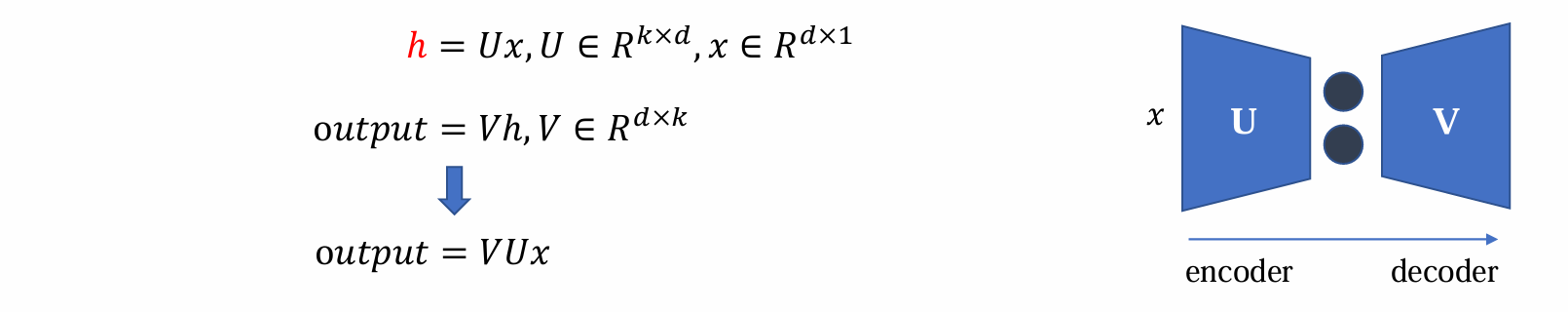
具体而言x通过线性变换由dx1变成kx1，变为隐层h实现encoder。h通过线性变换由kx1复原dx1变成输出output实现decoder
Note:
1. 这个网络是线性的
2. 通常设置k << d，如果k = d则可以使得VU = 1 从而为恒等变化而变得没有意义
3. 当 𝑘 ≪ 𝑑 时，实际上是对数据 𝑥 进行降维
优化目标：如何复原还原成output？output = VUx
如何确定V和U？可以考察 output 和 x 的 p 范数

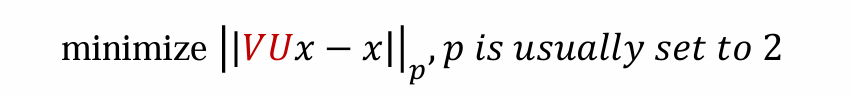
这时，encoder就相当于主成分分析(PCA)，可以通过最小二乘法求解
Note:
1. 解不唯一：若 𝑈∗ 和 𝑉∗ 构成一组解，则 𝑈∗ × 2 与 𝑉∗/2 同样构成有效解
2. 无需通过gradient descent求解该问题，存在closed-form 解，即通过有限次的标准运算和函数明确表达的解
autoencoder为什么要先encode降维再decode升维：先降维再升维的核心目的，是施加一种“信息瓶颈”(类似于主成分分析PCA)，强迫网络只能选择性地通过最重要的信息，从而抛弃冗余和噪声，学习到数据的本质结构。如果不经过这个瓶颈，网络最简单的做法就是直接复制输入（恒等映射），这就完全失去了学习意义

More about autoencoder

Autoencoder 通常可表述为 𝑓(𝑔(𝑥)) = x 的数学形式：
1. g函数是encoder
2. f函数是decoder
3. h = g(x)被称为 x 的 code / representation / latent variable
f 和 g 不应该过于复杂或者拟合能力过强：
1. 避免学习copy(encoder) 和 paste(decoder)
2. 避免过拟合
f 和 g 可以是浅层的神经网络：所有的参数可以通过梯度下降训练
Autoencoders 是可学习的以及 data-specific：
1. 这与 mp3 或者 jpeg 等压缩方法不同
2. autoencoder是数据相关的，在”cat images”上训练的autoencoder，在”dog images”上可能表现失效

Vanilla autoencoder is not a generative model

标准Autoencoder：它不是一个合格的“生成模型”，由于其训练目标是让输出 $\hat{x}$ 无限接近输入 $x$，它的中间隐藏层（latent representation）确实学到了数据 $x$ 的本质特征，但是隐藏层中的分布是“混乱的”和“未知的”
x 虽然服从数据分布但是数据分布是未知的，且不好假设的
而生成模型的定义为通过从 noise 中生成，得到去噪的结果，因此虽然AE可以压缩和解压缩，但是其没有涉及到随机分布、概率，且其分布不是可控、可建模的

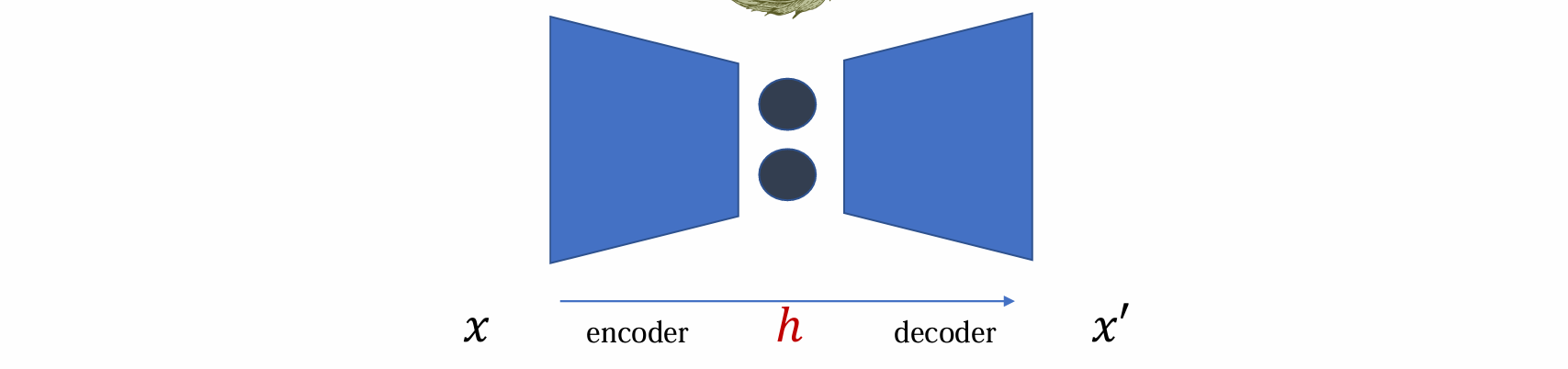
若训练完成后 ℎ 服从已知分布（如 standard Gaussian distribution），则将达到理想状态，可以用作生成模型

How to modify an autoencoder into a generative model?

当encoder被替换为random noise时，decoder即转变为generative model

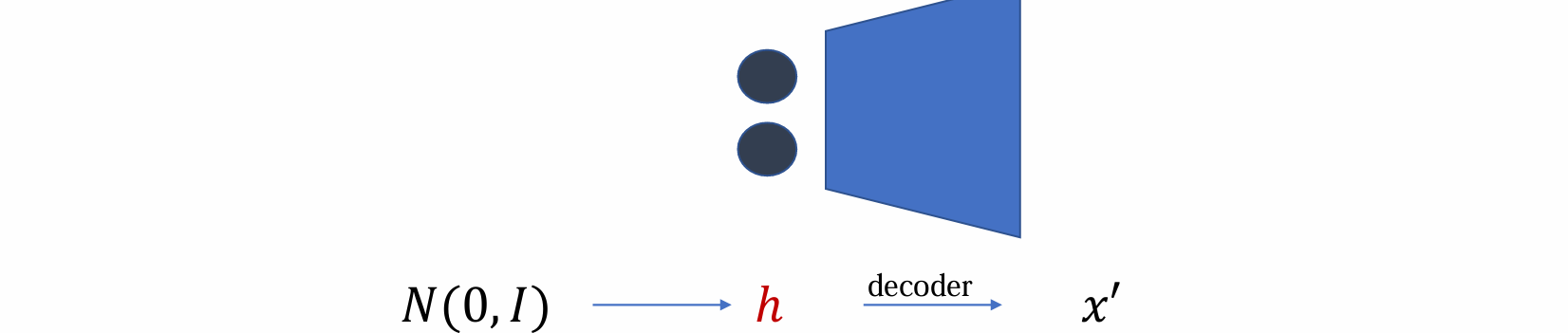
若保证h是已知(e.g.高斯噪音)则可去掉 encoder ，只用 decoder 作为生成模型
关键：如何使 h 在训练后变为已知分布？

Stochastic latent representation

在随机隐层表示中，h 是有随机性的随机变量，服从 g(x) 分布，而不是一个确定的值

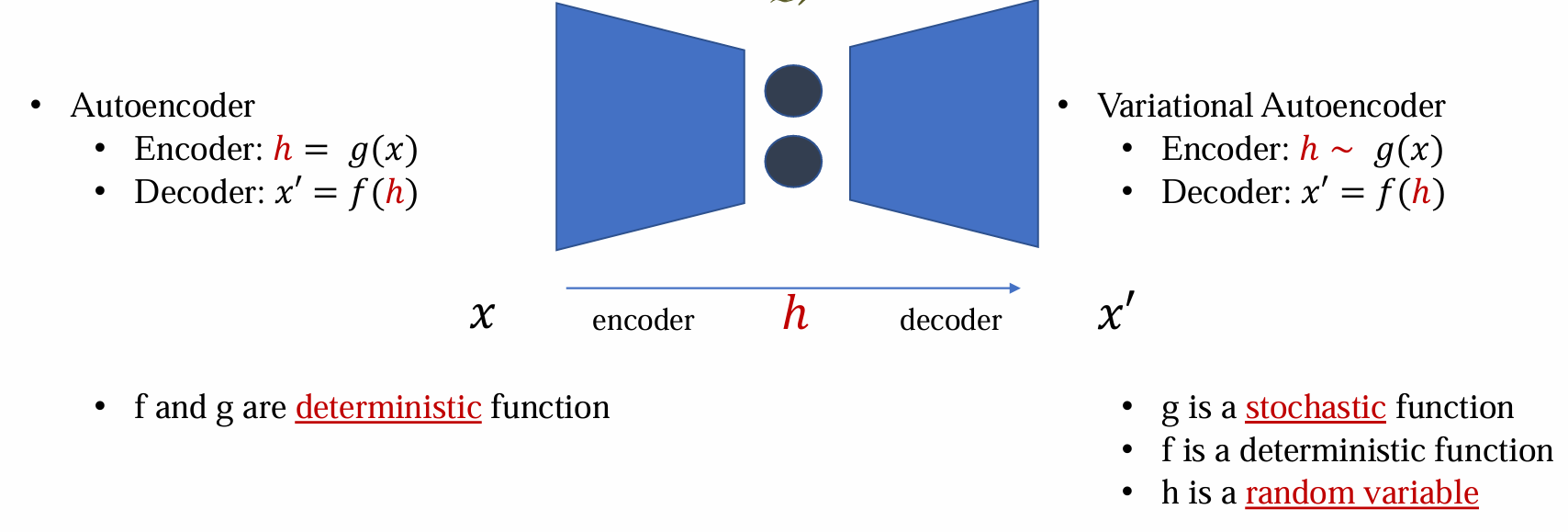
给出 x 后，神经网络的一部分生成均值，另一部分生成方差，根据均值和方差构建高斯分布
用神经网络构建的均值和方差都是可训练的参数

Examples

在 mnist 的例子中，第一个 hidden layer 有256维，通过 encoder 后变为100维得到第二个 hidden layer
在第二个 hidden layer中：
1. 50维用来预测均值
2. 另外50维用来预测方差
从而得到可学习的均值和方差，然后再通过这个均值和方差构建高斯分布

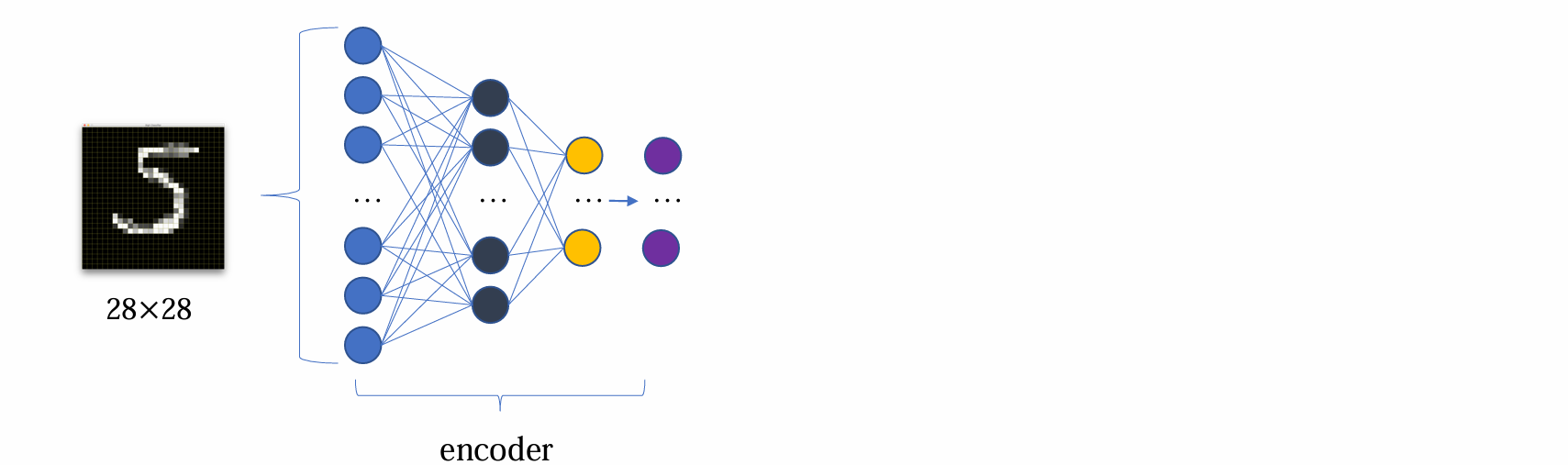
# encoder(incomplete)
class Encoder(torch.nn.Module):
    def __init__(self, D_in, H, latent_size):
        self.linear1 = torch.nn.Linear(D_in, H)
        self.enc_mu = torch.nn.Linear(H, latent_size)
        self.enc_log_sigma = torch.nn.Linear(H, latent_size)
        # 使用 log_sigma 是将[0, +inf)变为(-inf, inf)

    def forward(self, x):
        x = F.relu(self.linear1(x))
        mu = self.enc_mu(x)
        log_sigma = self.enc_log_sigma(x)
        sigma = torch.exp(log_sigma)
        return torch.distributions.Normal(loc = mu, scale = sigma)

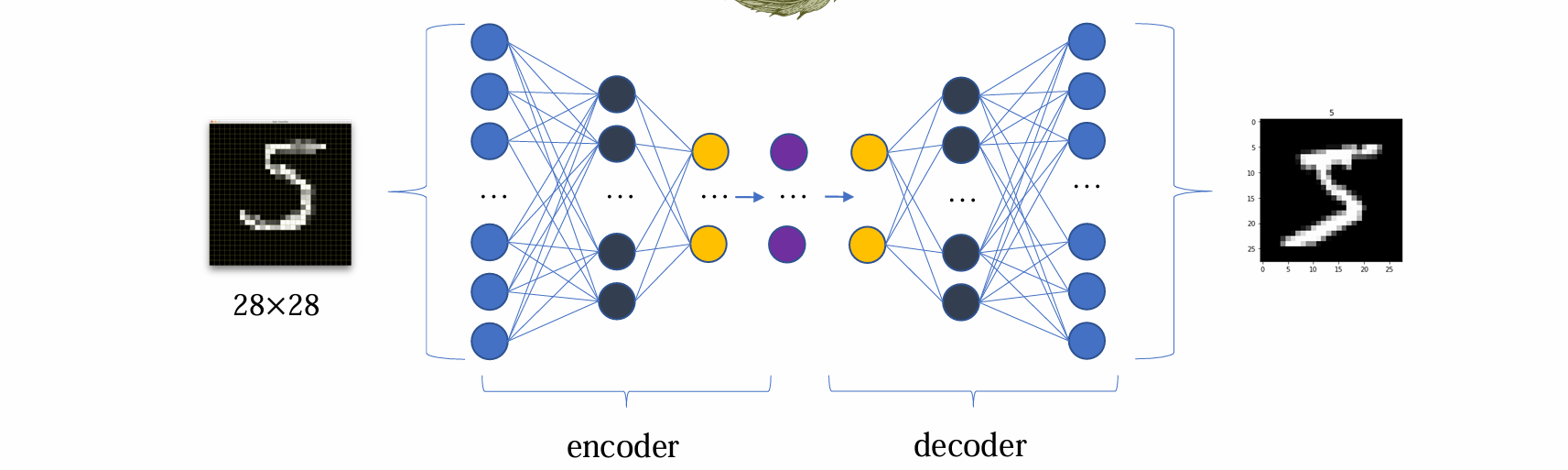
# decoder(incomplete)
class Decoder(torch.nn.Module):
    def __init__(self, D_in, H, D_out):
        super(Decoder, self).__init__()
        self.linear1 = torch.nn.Linear(D_in, H)
        self.linear2 = torch.nn.Linear(H, D_out)

    def forward(self, x):
        x = F.relu(self.linear1(x))
        mu = torch.tanh(self.linear2(x))
        return mu

    encoder = Encoder(input_dim, hidden_size. latent_size)
    decoder = Decoder(latent_size, hidden_size, input_dim)

encoder与decoder不一定具有对称性
encoder与decoder不一定必须是MLP(多层感知机)

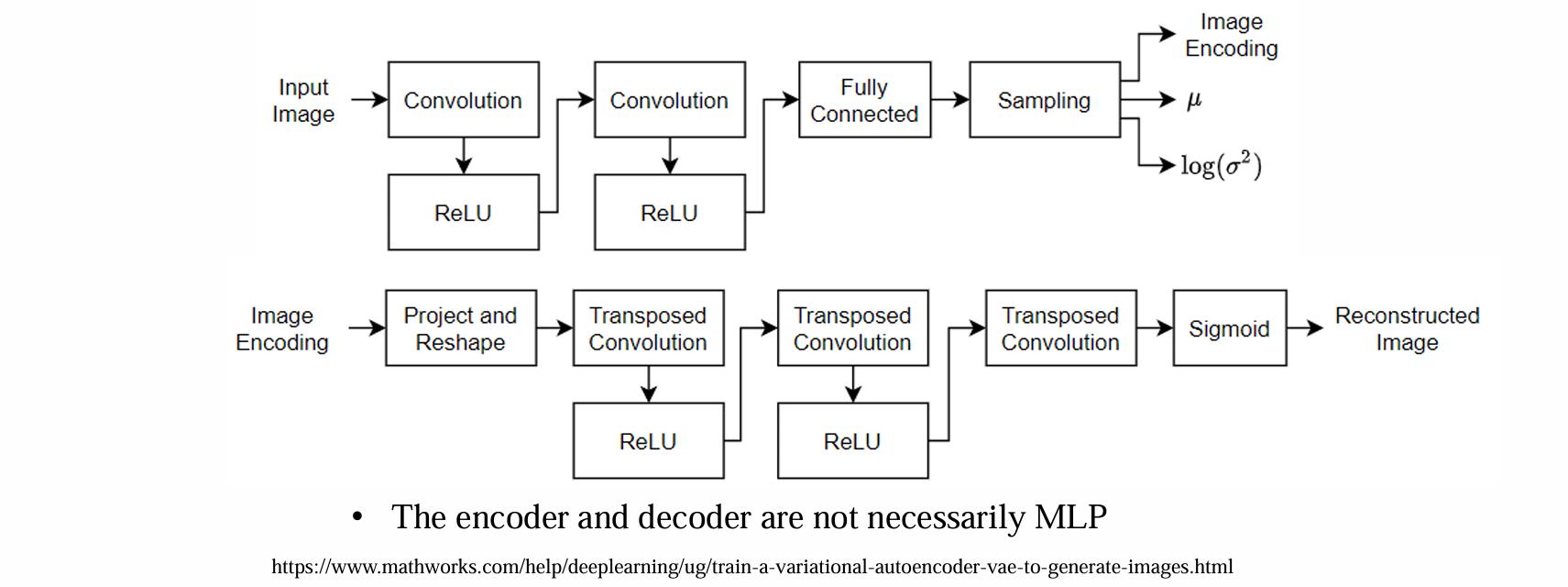
encoder的作用是得到可训练参数(均值、方差)的估计，decoder的作用是得到重构的image
问题：如何train？如何得到可估计的均值、方差？

Variational Autoencoder

Training VAE

pipeline：
1. 输入：x
2. 通过encoder得到均值方差的估计，根据均值方差的估计得到分布函数
3. 根据分布函数采样h
4. 通过decoder得到重构后的output，并优化x和output的距离

decoder参数的更新可以通过梯度的反向传播完成(都可以通过链式法则求导得到)：

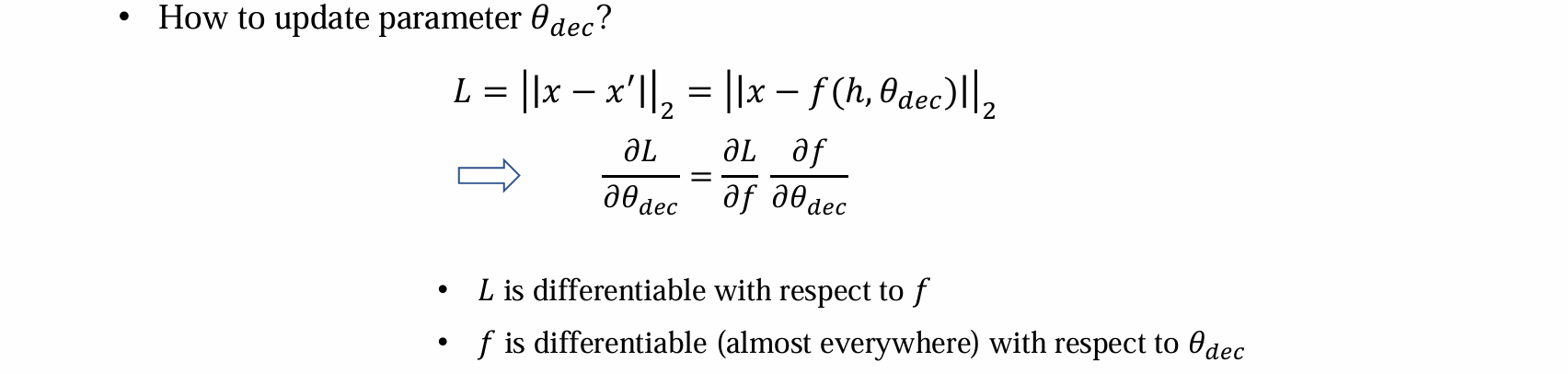
encoder参数的更新无法通过梯度的反向传播完成，因为h~g(x)是采样过程，不可导，导致不可训练：

VAE 的解决方法：Reparameterization trick(重参数化)

Key tech: Reparameterization trick(重参数化)

问题：采样过程是不可导的
解决方法：Reparameterization trick，将先 rescale 后 sample 变成先 sample 后 rescale，这个变化过程是完全等价的

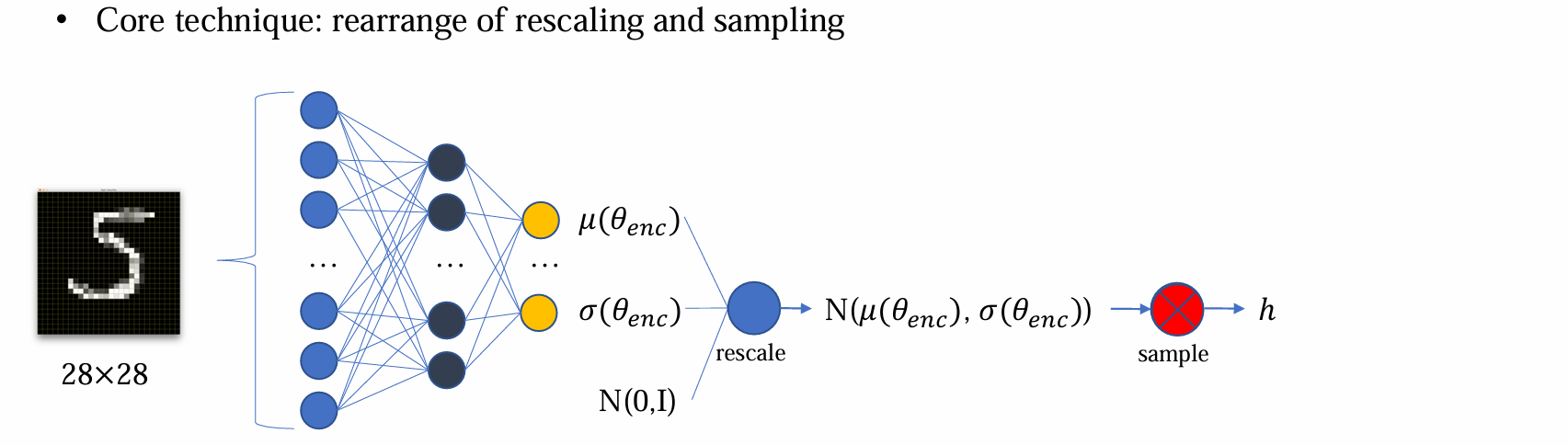
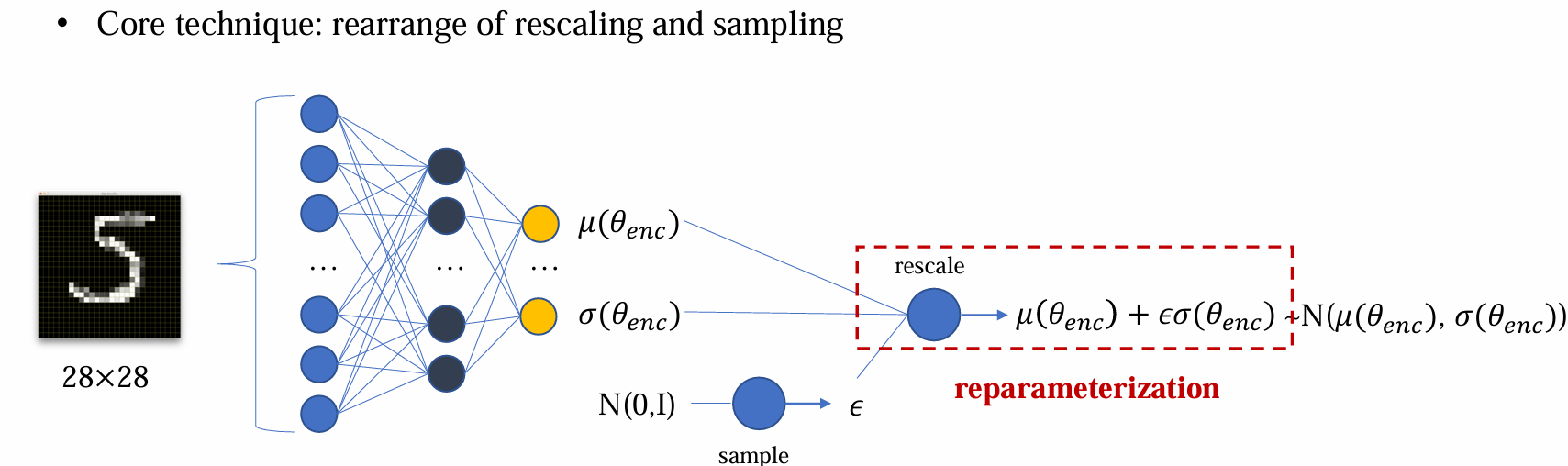
此时导数不会传到 epsilon 之前，整个过程都是可导的，可以训练均值和方差

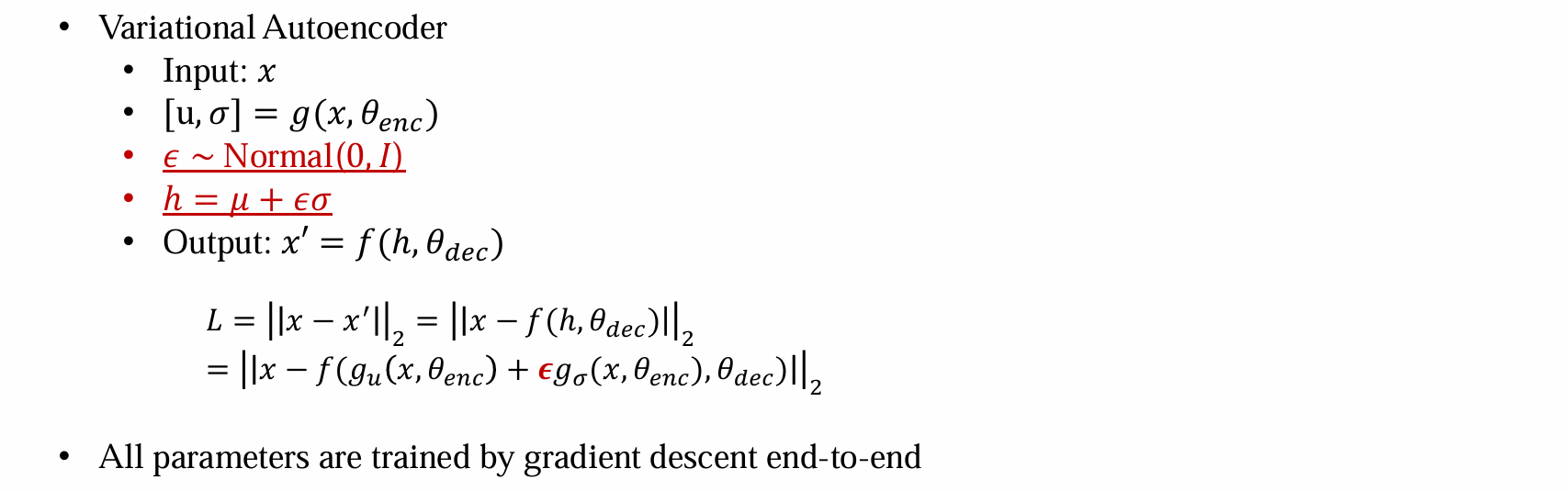
# VAE:implementation
class Encoder(torch.nn.Module):
    def __init__(self, D_in, H, latent_size):
        super(Encoder, self).__init__()
        self.linear1 = torch.nn.Linear(D_in, H)
        self.enc_mu = torch.nn.Linear(H, latent_size)
        self.enc_log_sigma = torch.nn.Linear(H, latent_size)

    def forward(self, x):
        x = F.relu(self.linear1(x))
        mu = self.enc_mu(x)
        log_sigma = self.enc_log_sigma(x)
        sigma = torch.exp(log_sigma)
        return torch.distributuins.Normal(loc = mu, scale = sigma)

问题：如何在训练后使 h 服从已知分布？
解决方法：设计regulation loss
1. 防止过拟合
2. 迫使编码器输出的潜在变量分布 q(z∣x) 逼近标准高斯分布 N(0,I)

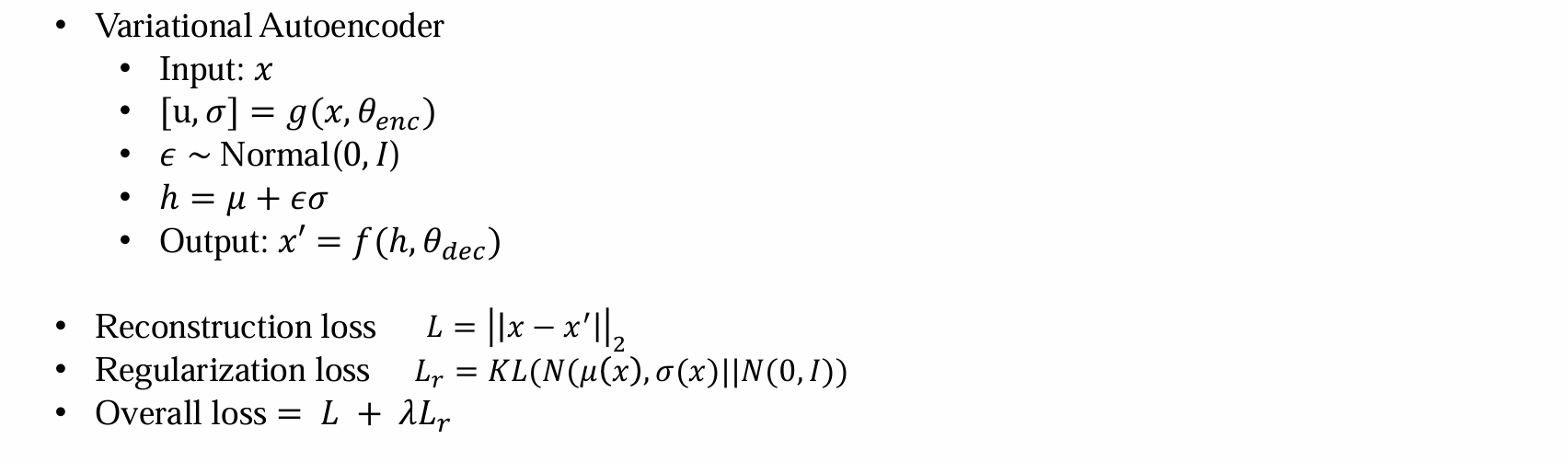
summary:

作为生成模型的时候，目的是从噪声恢复Image，因此只要 decoder

Probabilistic view of VAE(重点、必考)

问题：variational体现在哪儿

假设：data分布是存在且固定的，但是是未知的(e.g. 假设独立同分布)
VAE假设数据生成的过程：对于任何Image x，都有latent code z(e.g. 可以类比b站视频的分类标签)

latent code z 对于生成数据 x 有引导作用
latent code 未知，但是假设存在，可能无法解读
z 比 x 的 dim 小得多，可以容易得建模出 lantent code的分布
假设 z 服从分布 p(z)，称为：prior distribution
数据生成过程：假设p(z)已知，采样得到 zi，zi引导生成 x，得到xi，从而构建数据集 D = {xi}

问题：可以假设z为任意分布，已知p(z)、D，如何求解p(x|z)
利用最大似然估计可得：

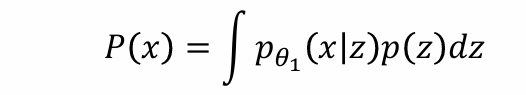
问题：没有方法可以对p(x)显式建模
最大似然估计的本质：最优的参数实质是最大化得到数据的概率p(x)

问题：神经网络过于复杂，无法进行估计(涉及高维积分和非线性函数)
根据显然事实假设：
1. 对于任意给定的 𝑧，在域 𝑋 中仅有小范围区域的点具有非零的 𝑝(x|z)，latent code 对应的数据 data 只有很少一部分符合
2. 假设我们有另一个函数/分布 𝑞𝜃2(z|x)，该函数/分布能够定位该区域，即给出x，可以推算出可能的z
函数/分布 𝑞𝜃2(z|x)被称为：Variational posterior distribution(变分后验分布)
等价化简过程：

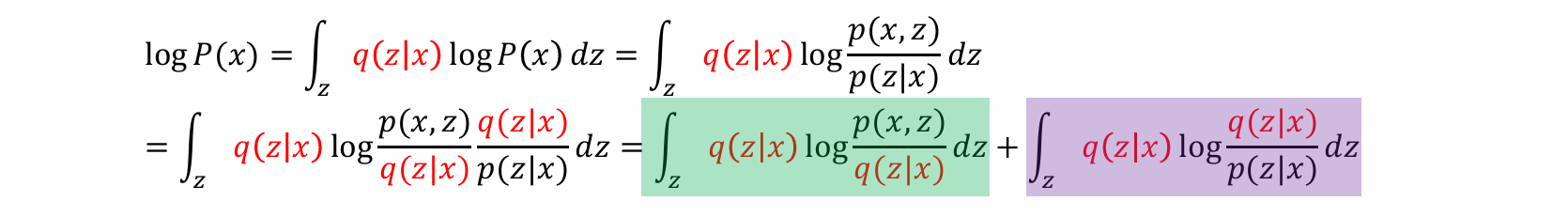
可以将log P(x) 化简为一下两部分之和：

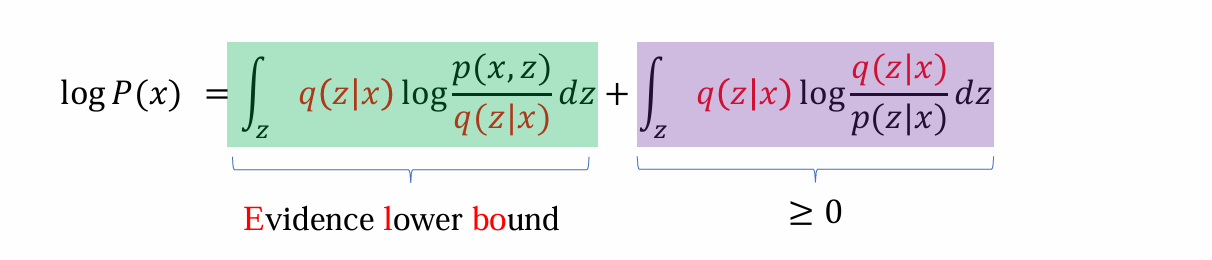
由于后面的式子显然≥0，因而前面的式子是log P(x)的lower bound 称之为：Evidence lower bound
虽然无法maximize log P(x)，但是由于Elbo是其下限，因而可以maximize Elbo，从而变相完成maximize log P(x)
将Elbo作为优化目标，进一步化简可得：

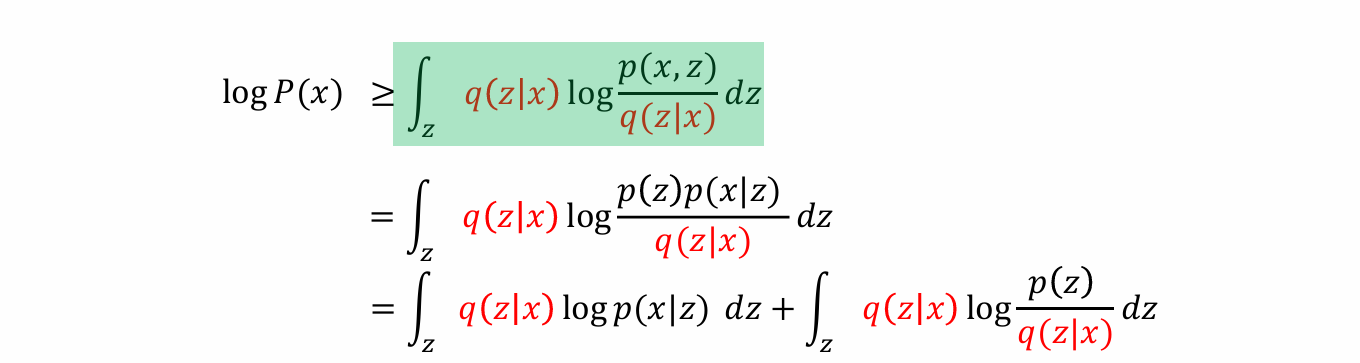
可知log P(x)的下限可以由两部分相加得到：

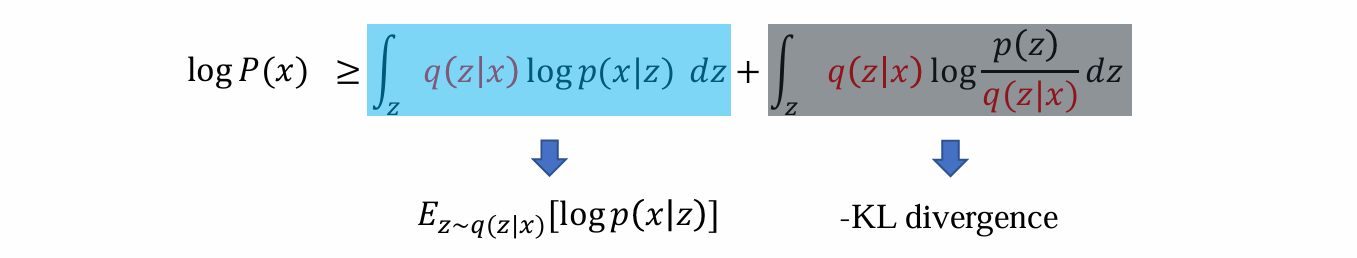
前面的式子：将q作为encoder，p作为decoder则说明能够还原出x的概率，某种程度等价于x和x’的loss
后面的式子：形式上与KL散度相近，某种程度等价于regularization loss

Problems in VAE

VAE 通常难以实现深度化，只能是浅层网络
latent code 的维度较为敏感
VAE 无法进行概率密度估计，即无法精确计算 p(x)
VAE通常只用作系统中的一部分，不单独使用

Extension：Denoising autoencoder

VAE 是在中间隐层 latent layer 中加入 noise，而 DAE 与之不同，是在 input 直接加入扰动

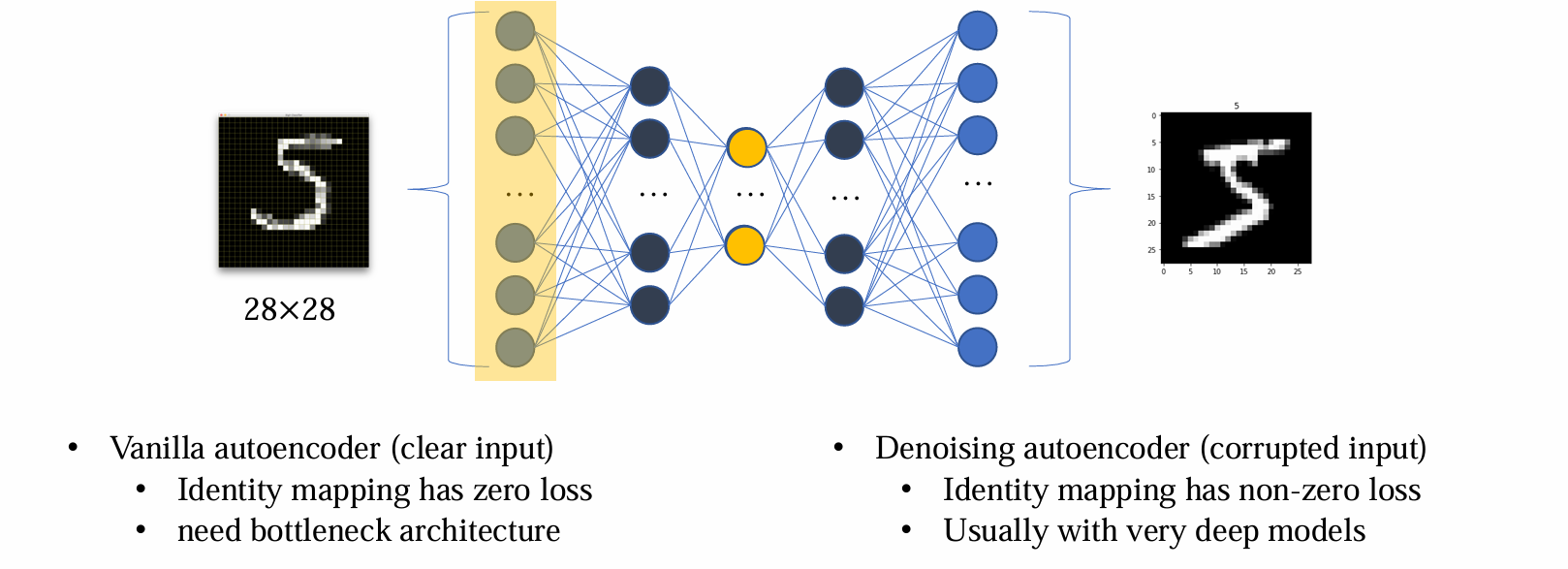
由于 DAE 不会发生过拟合问题，因而无需正则化。同时 DAE 没有显式区分 encoder 和 decoder
DAE 的实现流程：
1. Input:x
2. x’ = AddNoise(x)
3. Output X’’ = f(x’ θmodel)
如何加入噪声：使用 Mask 方式

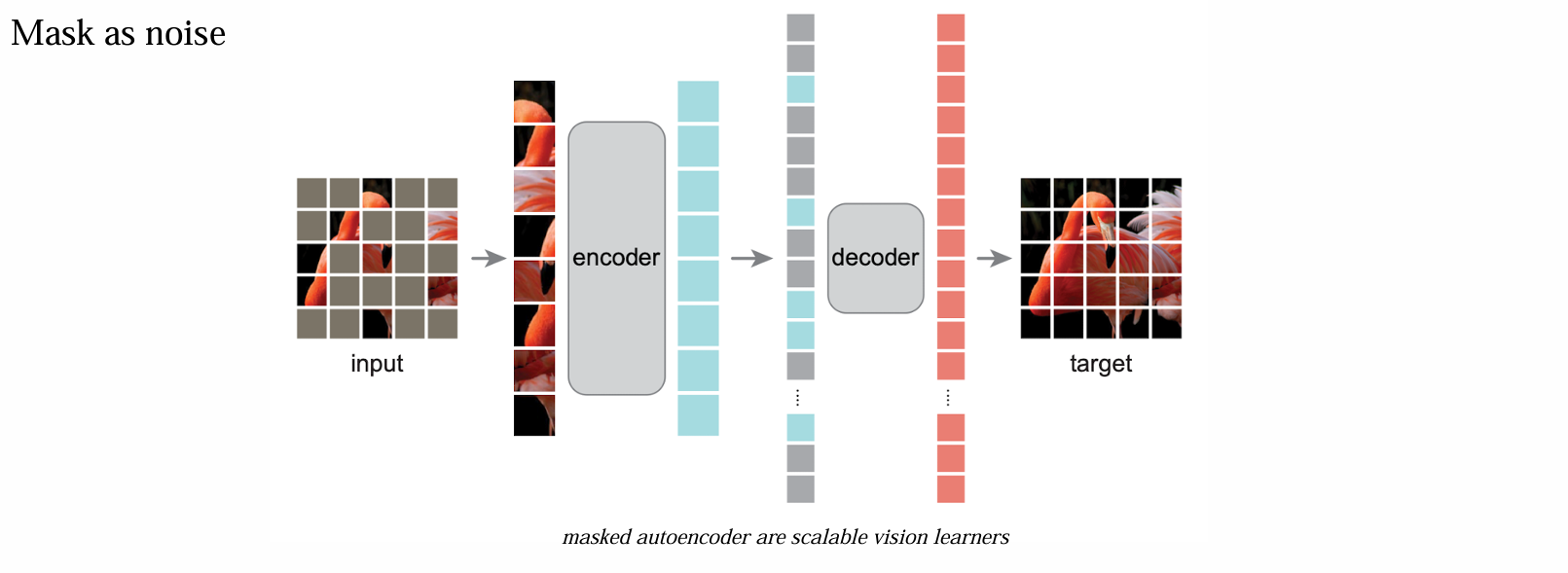
目标是复原 mask，一般 DAE 的 encoder 很深，而 decoder 较浅

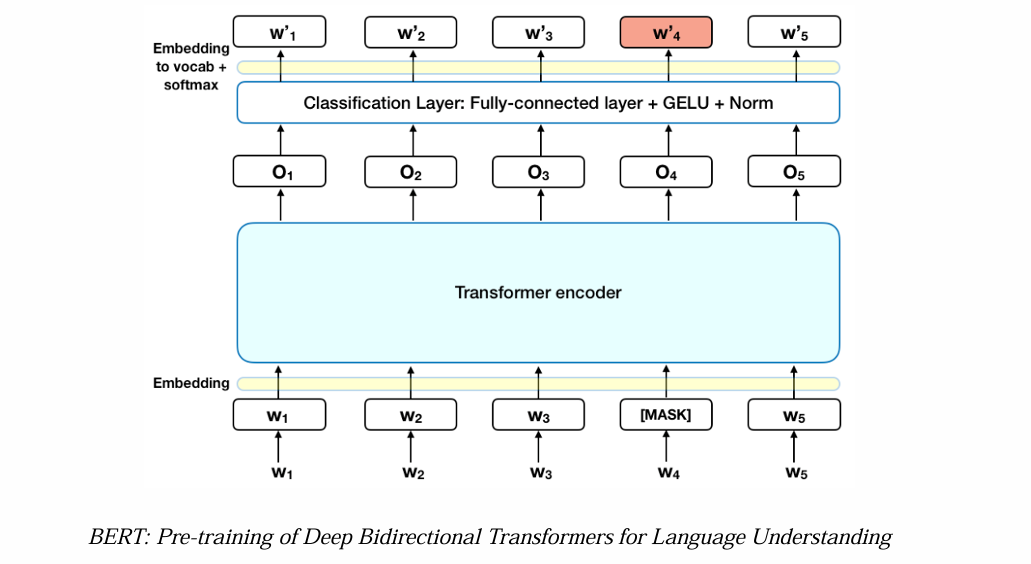
Denoising Autoencoder Summary：
1. DAE 几乎是唯一的 pre-training 方法
2. 标准化的加噪方式是采用 mask
3. 不受 VAE 的限制，可以并有必要训练很大的模型
4. 可以适用于任何形式的数据，只要能加噪即可
5. 虽然有一定生成能力，但是为 conditional 的生成，因而通常不被认为是生成模型，无法进行从0到1的生成

Extension：Vector-quantized VAE

VQVAE 通常作为系统中的一部分，不作为单独的模型使用
VQVAE 常用于多模态模型的生成和理解

Motivation

本质动机：image 和 text 非常不同，但是大量场景需要二者同时出现。理解、生成任务需要将两种信号有机结合
language 是由 tokens 组成的，拥有以下特点：
1. 有固定的词汇表，是有限的
2. 长度很短
3. 离散化
4. 可以通过vectors呈现：one-hot vector 或者进行 word embedding 后映射为 real vector
image 是由 pixels 组成的，拥有以下特点：
1. 没有词汇表
2. 长度很长(e.g. 1024 x 1024)
3. 可以被视为连续的(相邻像素间不会突变)
4. 可以通过 RGB vectors 呈现

Goal of VQVAE

将图像处理为一系列 “word tokens” 序列，使其带有语义信息
1. 如何为图像构建一个小的固定词汇表 vocabulary
2. 如何定义序列的长度
3. 如何将 RGB 值转换为 tokens

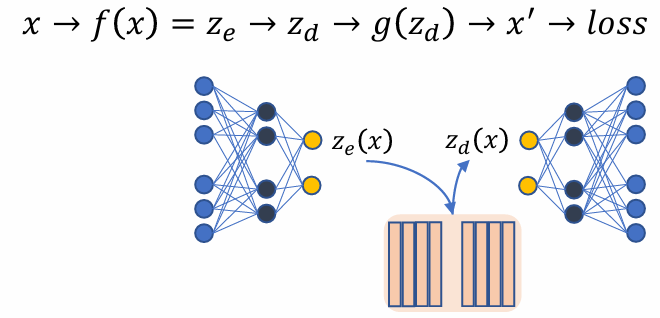
VQVAE model

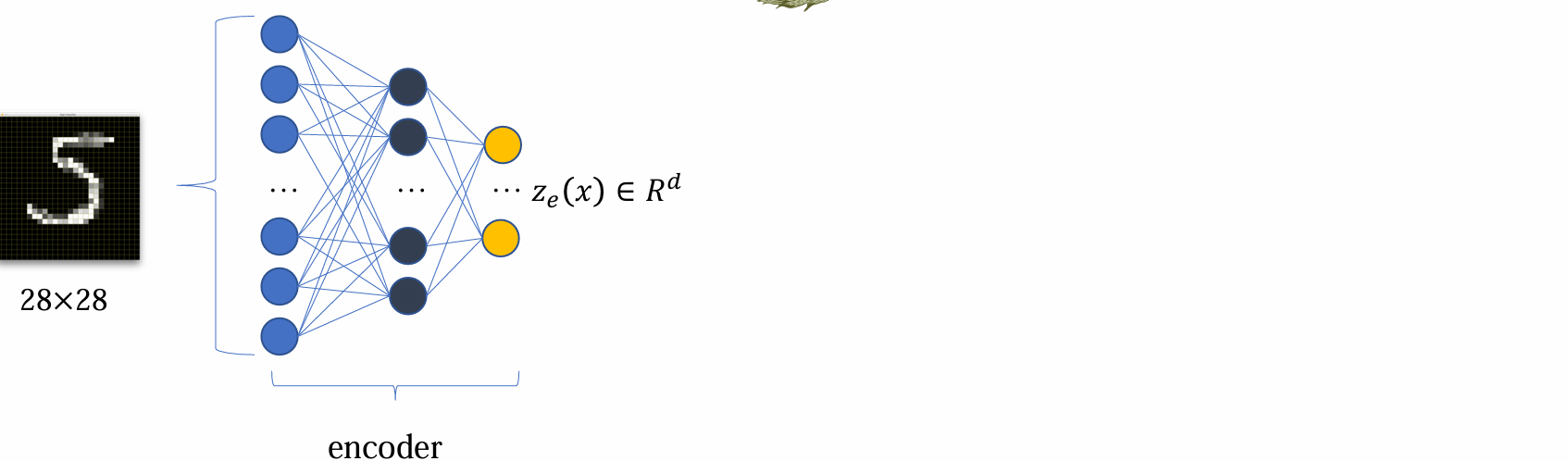
encoder 得到ze(x) 后，希望能够变成离散化，有限的表达，这一步骤通过codebook查表得到：

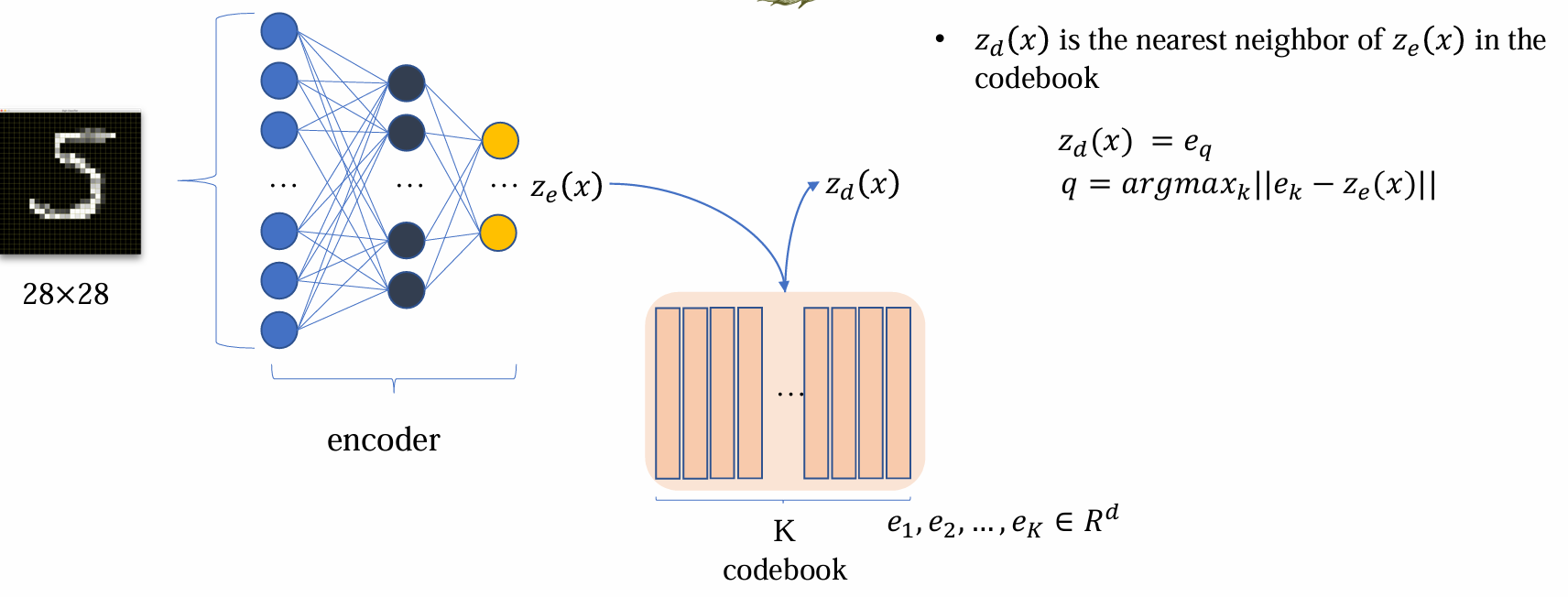
zd(x) 是 ze(x) 在 codebook 中的最近邻
不同于 VAE，VQVAE 的 latent 是查表后得到的
查表后得到的 zd(x) 为 decoder 的输入：

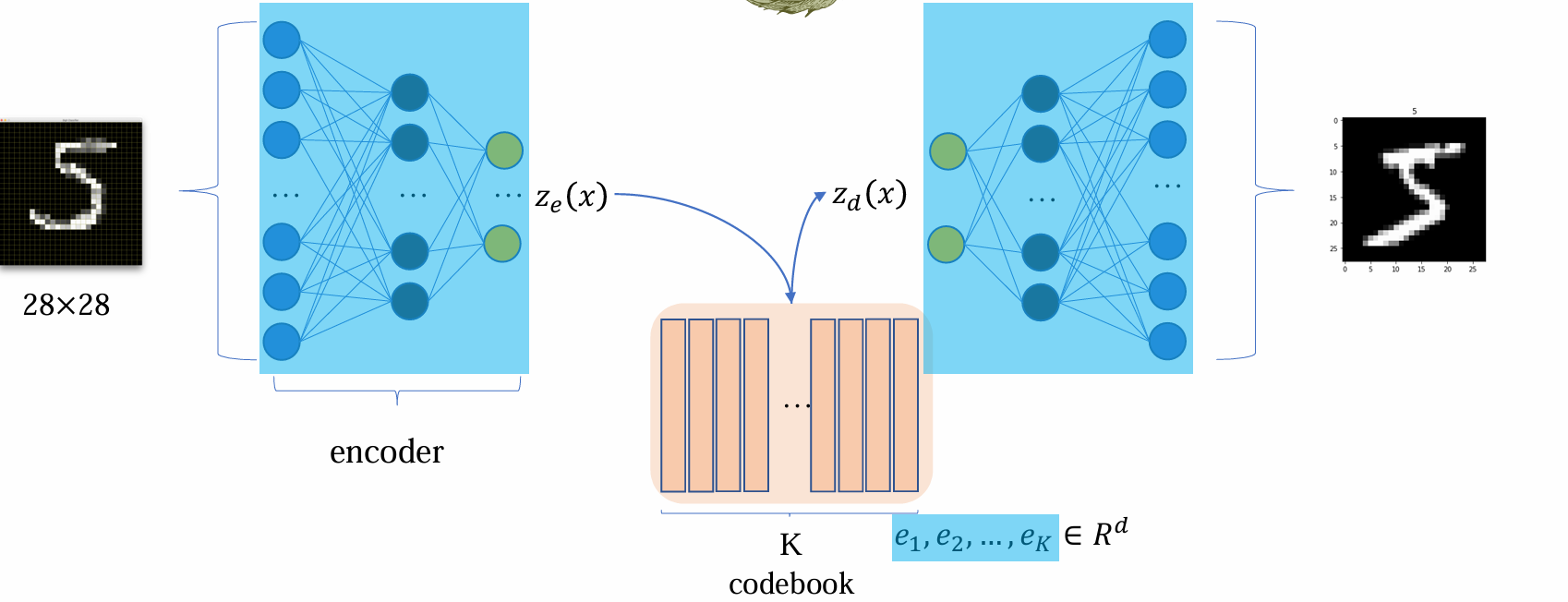
其中蓝色区域部分的参数是需要优化的，codebook 中的参数是需要优化的

Gradient computation

Gradient computation of encoder：

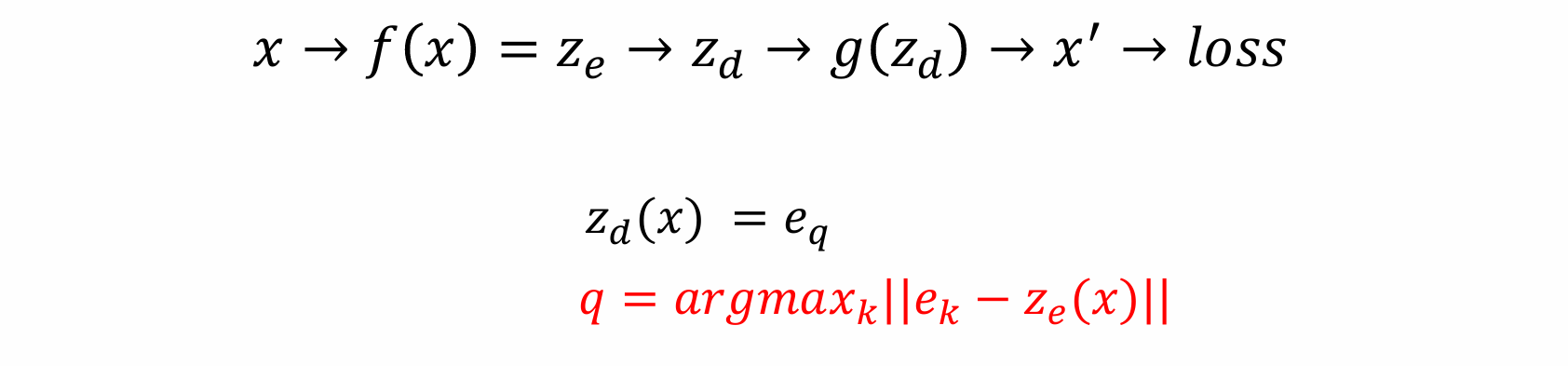
关键问题：codebook 无法计算梯度，codebook 的原理是求 argmax
1. 若采用 |𝑥 − 𝑔(𝑧𝑑)| 作为损失函数 loss，编码器参数 encoder parameters 将无法更新
2. 若采用 |𝑥 − 𝑔(𝑧𝑒)| 作为损失函数 loss，则优化目标 objective 已发生改变，梯度 gradient 不正确，所有参数 parameters 的梯度 grad 均错误
解决方法：设置 𝑧𝑑 = 𝑧𝑒 + StopGrad(𝑧𝑑 − 𝑧𝑒)，其中StopGrad(): gradients in the argument will be never calculated
实质上是用另一种方法做重参数化
损失形式：x − 𝑔(𝑧𝑒 + StopGrad (𝑧𝑑 − 𝑧𝑒)) ||
1. 正确的前向传播过程
2. decoder 参数可以正确反向传播
3. encoder 参数可计算更新，在 d 和 e 间建立可导通路

Update of the codebook

希望 codebook 是有意义的
codebook loss：||𝑧𝑒 − StopGrad(𝑧𝑑)|| + 𝛽 ||𝑧𝑑 − StopGrad(𝑧𝑒)||
VQVAE loss = reconstruction loss + codebook loss

生成模型基础 02 Autoencoders

Autoencoders

Basics

What is autoencoder?

Why autoencoder?

The simplest autoencoder(线性autoencoder)

More about autoencoder

Vanilla autoencoder is not a generative model

How to modify an autoencoder into a generative model?

Stochastic latent representation

Examples

Variational Autoencoder

Training VAE

Key tech: Reparameterization trick(重参数化)

Probabilistic view of VAE(重点、必考)

Problems in VAE

Extension：Denoising autoencoder

Extension：Vector-quantized VAE

Motivation

Goal of VQVAE

VQVAE model

Gradient computation

Update of the codebook

Improving capacity