生成模型基础 07 Normalizing Flow

Normalizing Flow

Looking back

• VAE特点：

  1. 浅层网络
  2. 非序列化
  3. 重建进行复原image

• Autoregressive特点：

  1. 深层网络
  2. 序列化
  3. 可以通过MLE优化

• GAN特点：

  1. 深层网络
  2. 非序列化
  3. 通过近似距离用神经网络评估

• 希望非序列化(image 难以表征为序列)，但是可以通过MLE进行优化 -> Normalizing Flow

• Normalizing Flow的特点：

  1. 深层网络
  2. 非序列化
  3. 可以通过MLE优化

• normalizing flow和AR的区别：normalizing flow是非序列的；换相比于VAE和GAN，可以计算密度，从而可以使用MLE方法优化

• 标记法：

  1. image -> x
  2. noise -> z
  3. generator -> g(z)
  4. 目标：学习g(z)，使得g(z)生成结果接近于x

• 生成模型的流程可由下图所示，我们希望设计一个方法使得给定任意x，我们都能计算出使用生成模型生成出这个sample的概率密度p(x; θ)

• 若似然函数已知，则可以用MLE进行优化

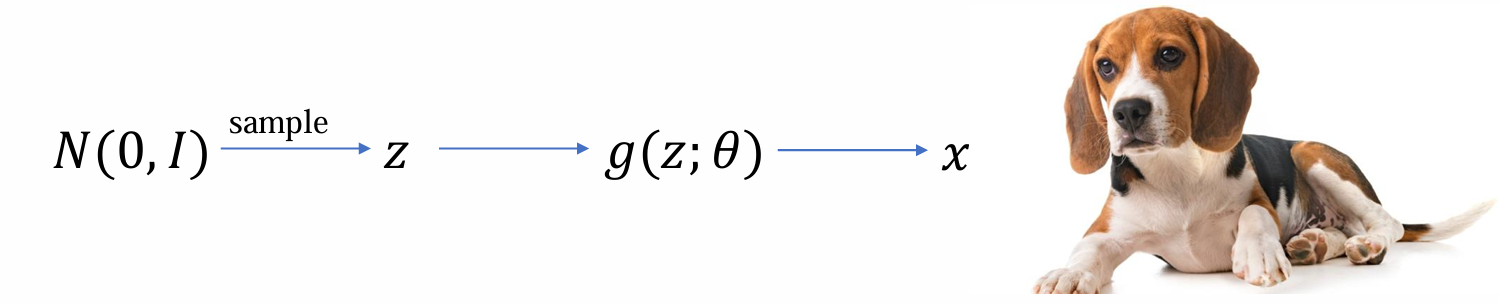
• 思路：若g(z)可逆，则给定x可以通过g(x)的反函数得到唯一的z，也就是说x和z一一映射，相互唯一确定。那么如果z可算(简单分布) -> x的概率可算

---

The change of variables theorem: one dimensional

• 设𝑍是一个具有概率密度 𝑝𝑍(𝑧) 的随机变量，𝑋=𝑔(𝑍)，其概率密度为 𝑝𝑋(𝑥)(下标是关心的变量)

• 假设𝑔有可逆函数𝑔−1，为方便起见，𝑔是单调递增的，且g和g-1都是可导的，从而可以推出：

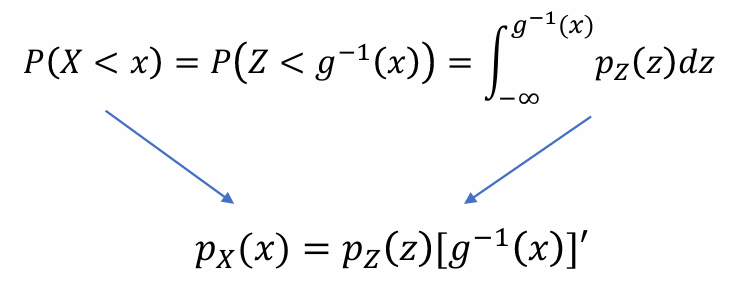
• 问题：[g-1(x)]’该怎么化简，希望右侧都是变量z，由于：

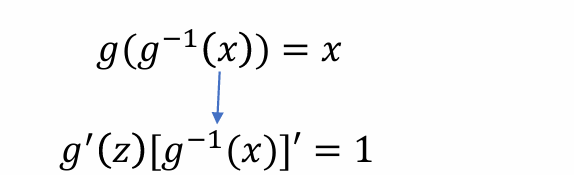
• 从而带入可得(g:z -> x)：

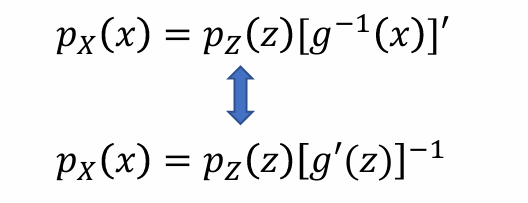
• e.g.：ZU(0, 1)，若X = 2 * Z，则XU(0, 2)，根据上述公式可得：

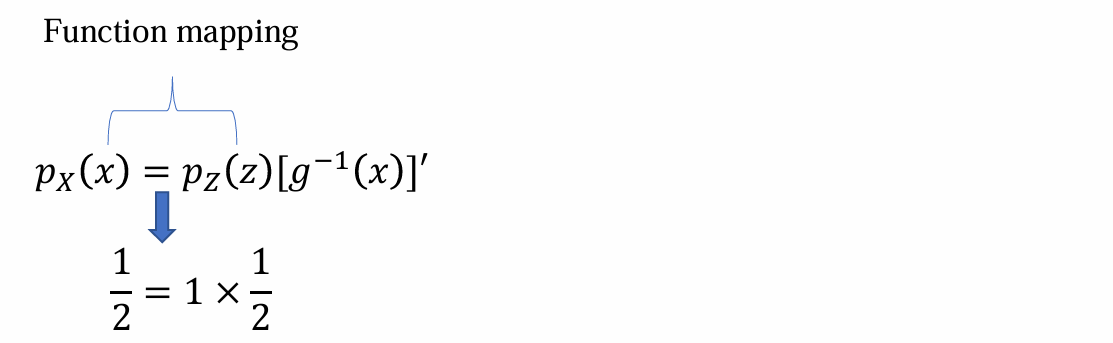
• 给定数据集：𝐷 = {𝑥1,….,𝑥𝑛}，则：

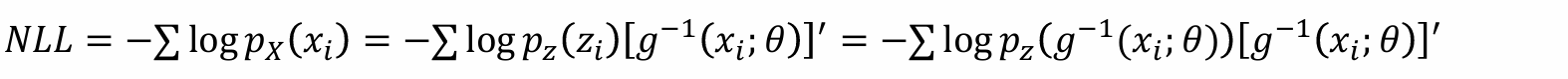
• 虽然上式可算，但是问题是对model有很强的假设：
  1. z <-> x 可逆
  2. 反函数及其导数可算
  3. 并且对模型θ的导数可算

---

High-dimensional case

• 设𝑍∈ℝᵈ 是一个具有概率密度 𝑝𝑍(𝑧) 的随机向量，𝑋=𝑔(𝑍)∈ℝᵈ 是一个具有概率密度 𝑝𝑋(𝑥) 的随机向量。g：ℝᵈ -> ℝᵈ是可逆的且可导(Diffeomorphisms (微分同胚))

• X由Z生成，而Z可以认为由Z1,…,Zd组成，因此： 𝑥=𝑔(𝑧)=(𝑔1(𝑧1, …,𝑧𝑑) ,…,𝑔𝑑(𝑧1, …𝑧𝑑))

• 导数为雅各比矩阵：

• 由一维的公式拓展到高维可得以下公式，对其进行化简，vol为一个小的体积单元：

• 生成器 𝑔 将简单概率密度 𝑝𝑍 推进到更复杂的密度 𝑝X

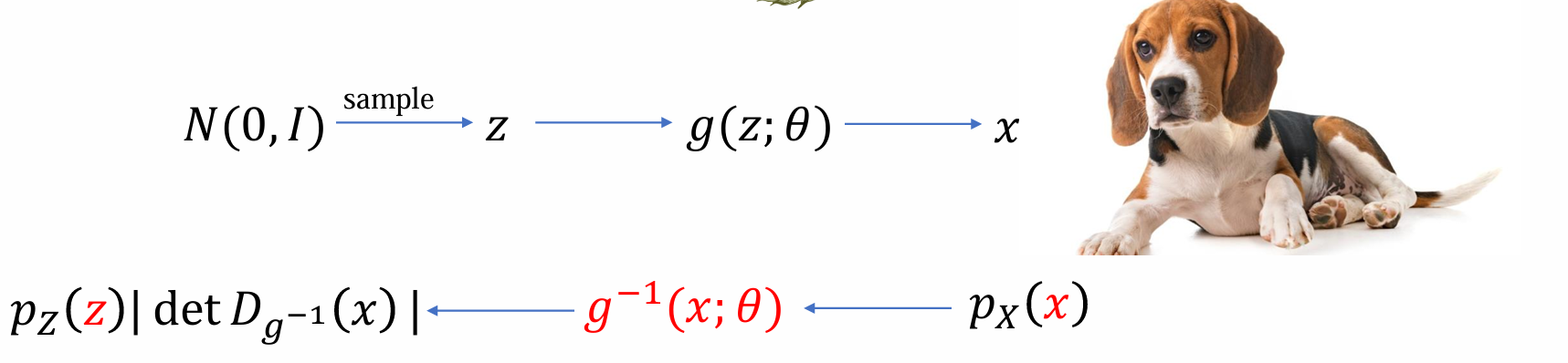
• 逆函数 𝑓 = 𝑔−1 的运动方向相反(flow)：将复杂分布 𝑝𝑋 归一化(normalizing)为更规则的简单分布 𝑝𝑍

• flow：反过来回传，将复杂的分布归一化为一个简单的噪音

• 可以计算每个样本的似然函数，从而通过计算梯度来进行优化

---

Connection to VAE

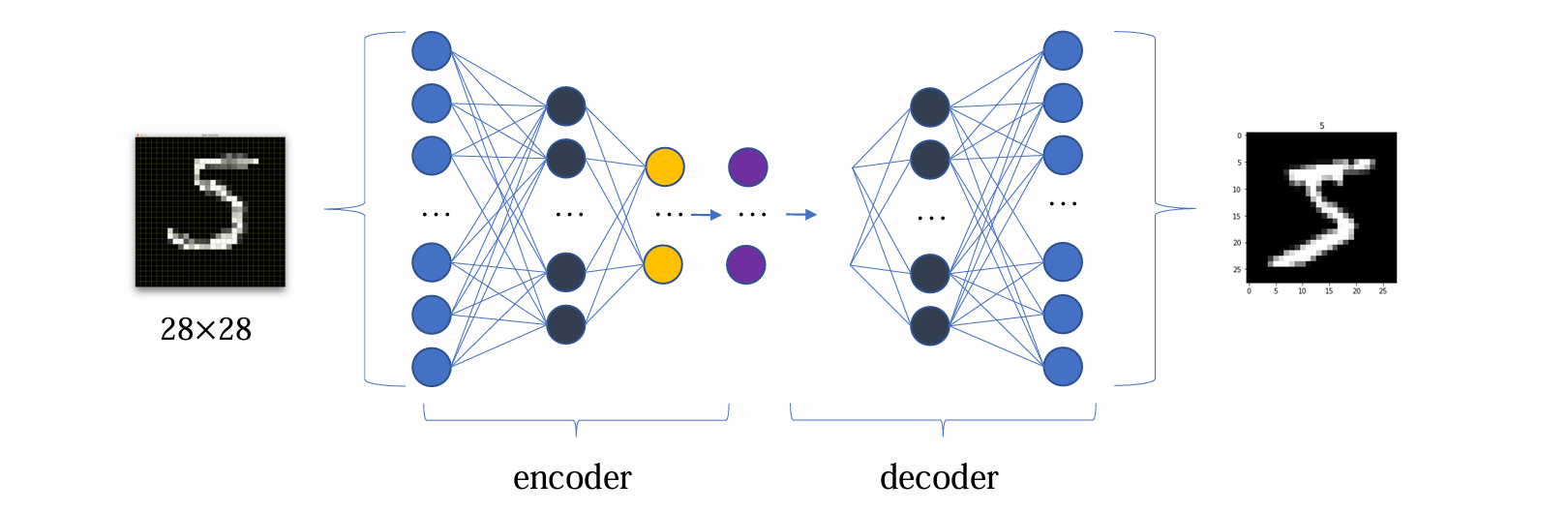
• decoder可以理解为：给定z，生成x

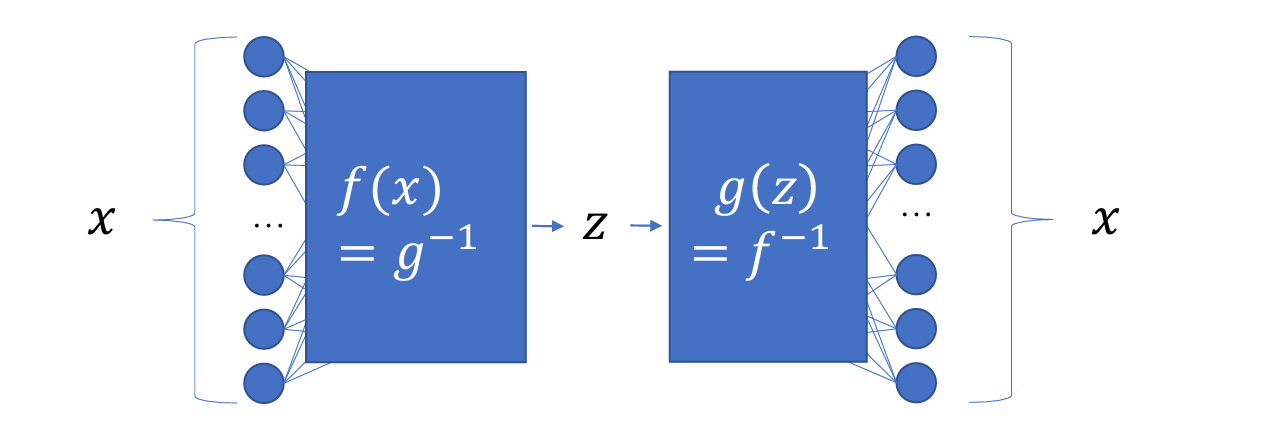
• 但是normalizing flow的设计理念和VAE有很大不同，和VAE的本质区别在于：
  1. encoder和decoder有更高的要求，需要二者为严格的反函数，而VAE没这个要求
  2. normalizing flow可以用比较深的模型

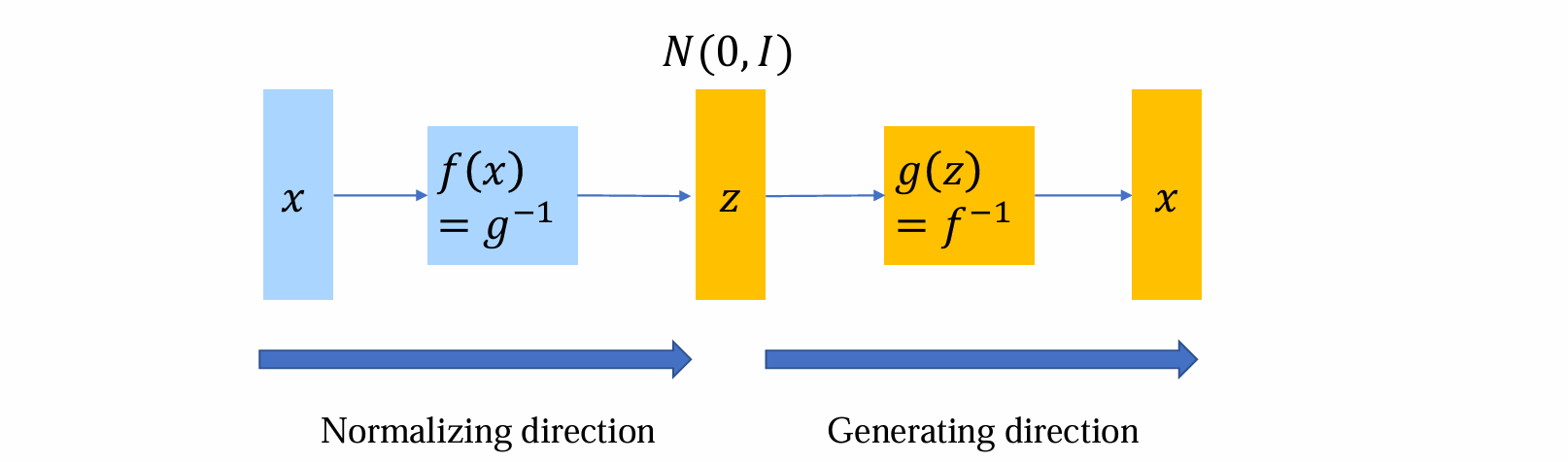
• normalizing direction：起到encoder的作用，将复杂的分布进行归一化

• 而normalizing flow计算的时候，既可以通过g:z -> x计算，也可以通过f:x -> z计算

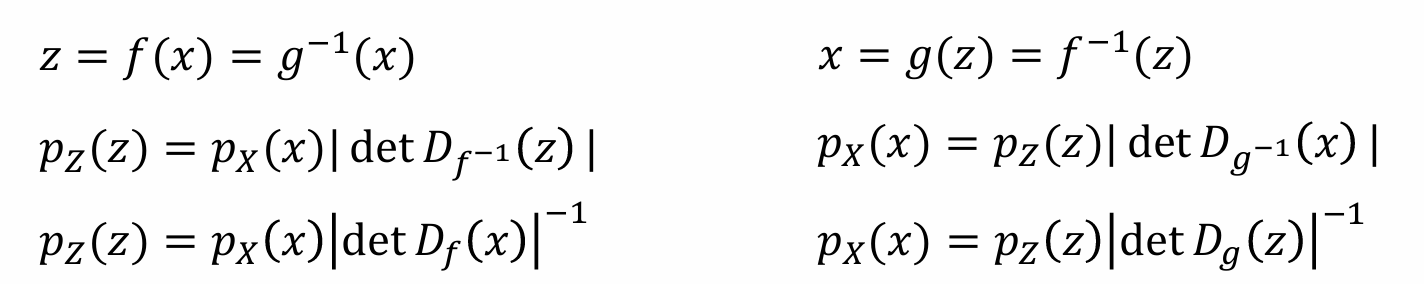
• trick in practice：可以用两套不同的参数化方法处理x和z，同时既可以选择参数化g，也可以选择参数化f

• 实际应用中选择f和g的效率会很不同，通常只会选择一个进行参数化，否则不能保证为反函数

---

Applications: density estimation

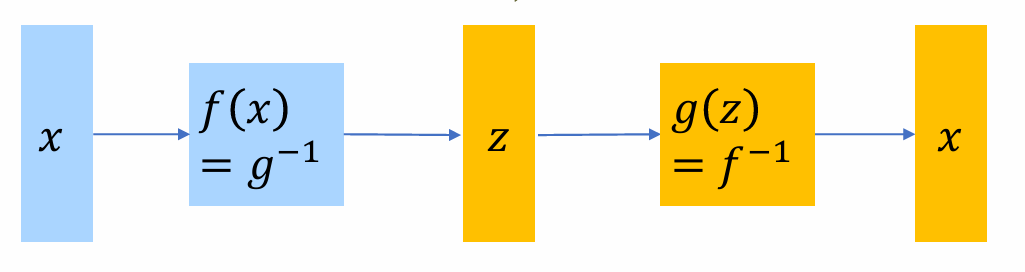
• 概率密度估计的目标：给定x，输出是p(x)的估计

• 应用场景：

  1. 概率模型的输出具有随机性，但实际应用中需要选出最好的，因此需要根据概率密度排序选出最佳
  2. 异常检测/新颖检测，MLP计算出概率低的值

• 假设我们已经有了模型(f or g)

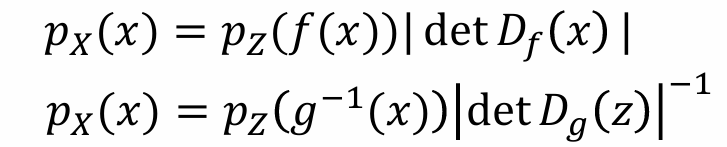
• 若参数化f：f(x) = z，可以通过计算p(z)和计算行列式的绝对值求出

• 若参数化g：需要先算出g-1，再按照f的方法计算

• 因此对于概率密度问题，参数化f无需计算反函数，因此应该参数化f

---

Applications: sampling

• 采样的目标：和生成模型目标接近，给定噪声z，希望输出复杂分布p(x)

• 应用场景：生成模型

• 假设我们已经有了模型(f or g)

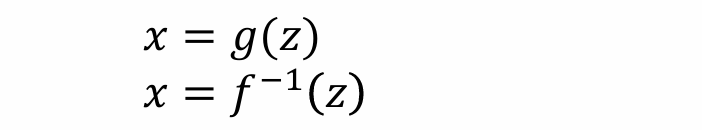
• 显然参数化g无需计算反函数，对于采样任务应该参数化g

---

Challenge

• 问题：用神经网络建模f,g涉及多种复杂的非线性操作，映射复杂，无法保证其是否可逆

• 因而需要对网络做特殊的要求限制

• 核心挑战：在normalizing flow中，需要找到一个可以计算映射的函数类

• 要求：这个函数类需要是方便计算、求逆以及求其雅可比行列式的行列式

---

Constructing flow: basic properties

• flow的模型层需要是可逆函数复合成的：假设g1,g2存在反函数，且都可导，都可对θ求导，那么复合函数𝑔(𝑧) = 𝑔2◦𝑔1(𝑧)=𝑔2(𝑔1(𝑧))也是可逆的

• 𝑔−1 = 𝑔1−1 ◦ 𝑔2−1 = 𝑓1 ◦𝑓2

---

Composition of layers

• • normalizing flow的layer由多个可逆的layer(多可可逆变换)串行形成

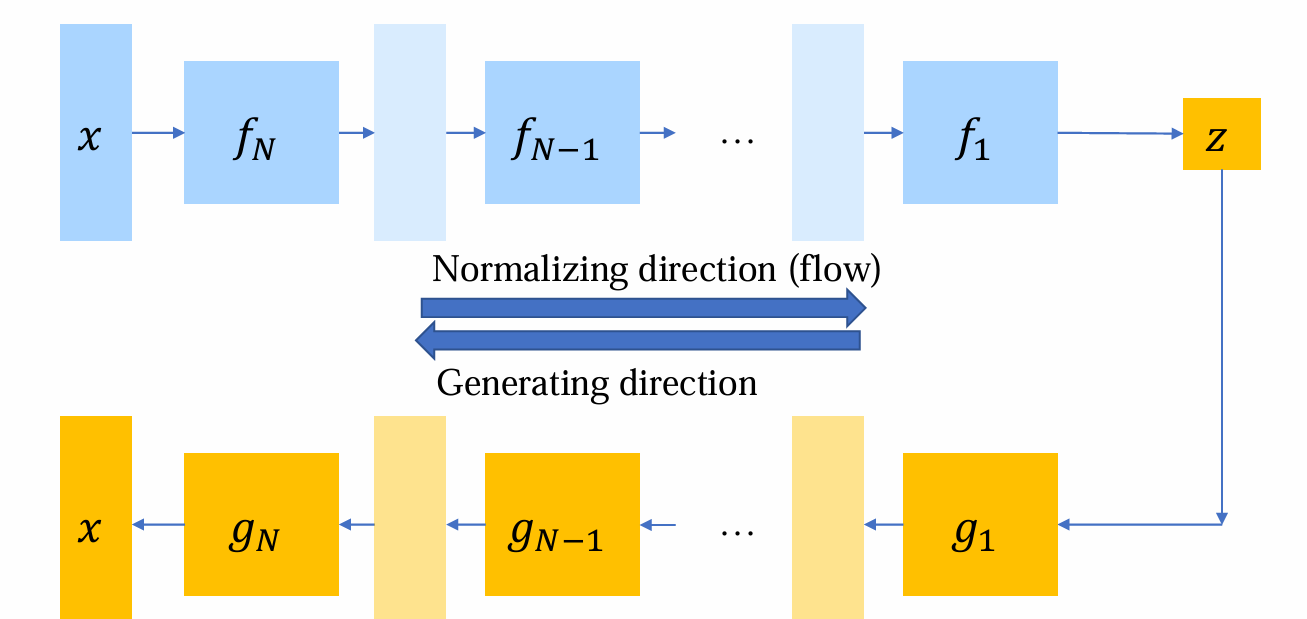
• 问题：如何构建基本单元？组合函数的Jaccobi怎么计算？

• Composition of invertible functions：设 𝑔(𝑧) = 𝑔𝑁 ◦⋯◦ 𝑔1(𝑧),𝑥𝑛 = 𝑔𝑛◦…◦𝑔1(𝑧)是经过g1,…,gn变换的结果，若n=N则为x

• Composition of Det：

---

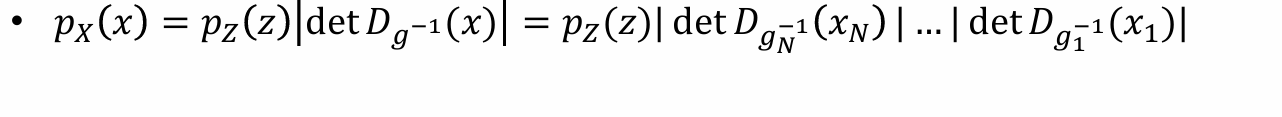
Elementwise flow

• 逐元素，每个元素执行相同的函数h：𝑔(𝑧) =(ℎ(𝑧1) ,ℎ(𝑧2) ,…ℎ(𝑧𝑑))

• 如果h是可逆的，那么g(z)是可逆的

• 其中h可以是任何合理的激活函数

• 问题：没有提取不同维度间的相关性，没有提炼“特征”

• 优点：简单，计算效率很高；缺点：表达能力差

---

Linear flow: 𝑔(z) = 𝐴𝑧 + b

• 𝑔(z) = 𝐴𝑧 + b，其中A是dxd矩阵，b是偏置

• 如果A是可逆的，那么g(z)可逆，g−1(𝑥) =𝐴−1(𝑥−𝑏)，并且具有以下性质：

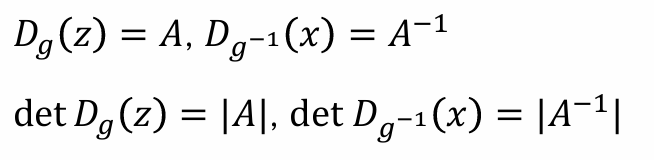
• 问题：计算一般矩阵的行列式需要 𝑂(𝑑³) 的成本，效率很低

Linear flow with triangular matrix

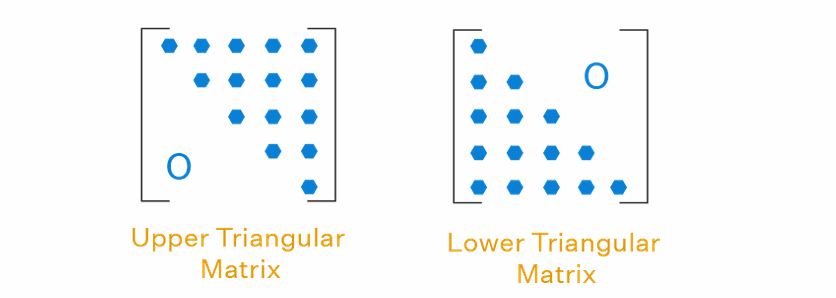
• 形式仍然是 𝑔(𝑧) = 𝐴𝑧 + b，如果𝐴是对角线元素非零的三角矩阵，那么𝐴是可逆的

• 根据三角矩阵的性质可得：

• 计算逆矩阵需要 O(d²) 的成本

---

Linear flow with orthogonal matrix

• 形式仍然是 𝑔(𝑧) = 𝐴𝑧 + b，如果𝐴是正交矩阵，那么𝐴是可逆的

• 根据正交矩阵，具有以下性质：

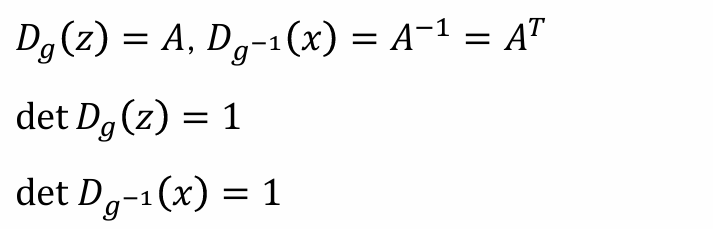
• 由于正交矩阵的逆矩阵可以直接求出，所以x ->z和z ->x的计算代价完全一致

• 正交矩阵的行列式为1或者-1，可以通过参数化的方法使其为1

• 问题：要求训练过程中始终保持正交矩阵，然而朴素的方法无法保证梯度回传后仍然是正交矩阵

• 解决方法：技巧：参数化v，在v中计算

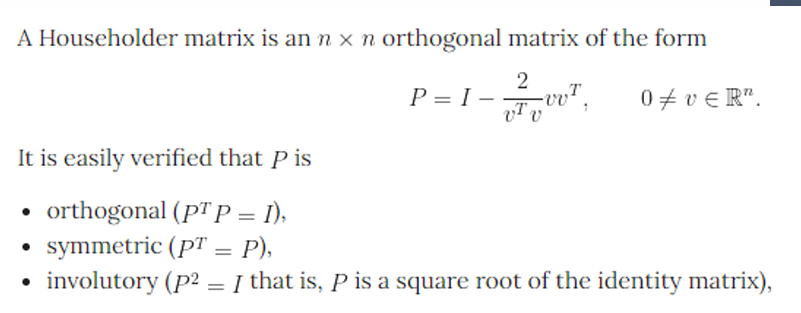
• 将上述 linear flow and elementwise flow组合起来，类似于MLP

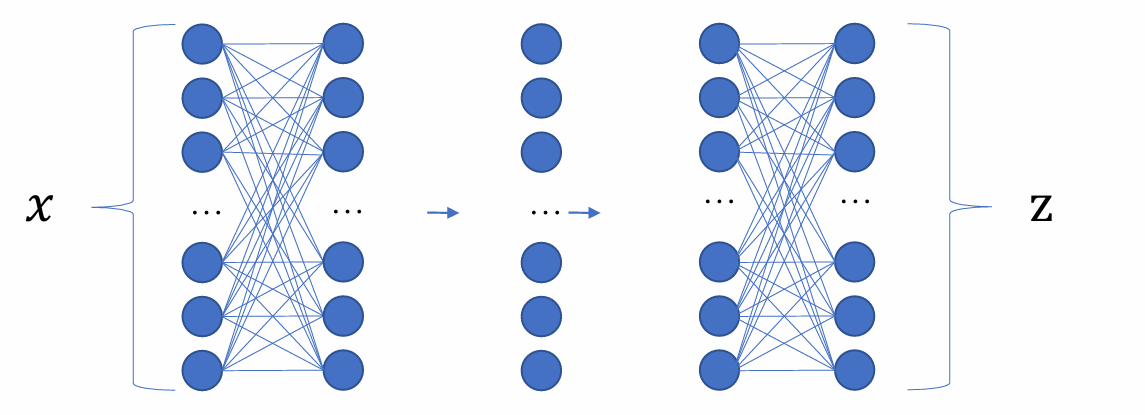
• 优点：表达能力很强；缺点：效率很低，无法在实际中应用

---

Residual flow 1

• g(𝑧) = 𝑧 + ℎ(𝑧)，可以将z人为拆成两个部分：𝑧=(𝑧1,𝑧2), 𝑧1 ∈ 𝑅𝑑1 𝑧2 ∈ 𝑅𝑑−𝑑1

• 然后对z1,z2应用变换，注意x2计算h2作用于x1上而不是h1

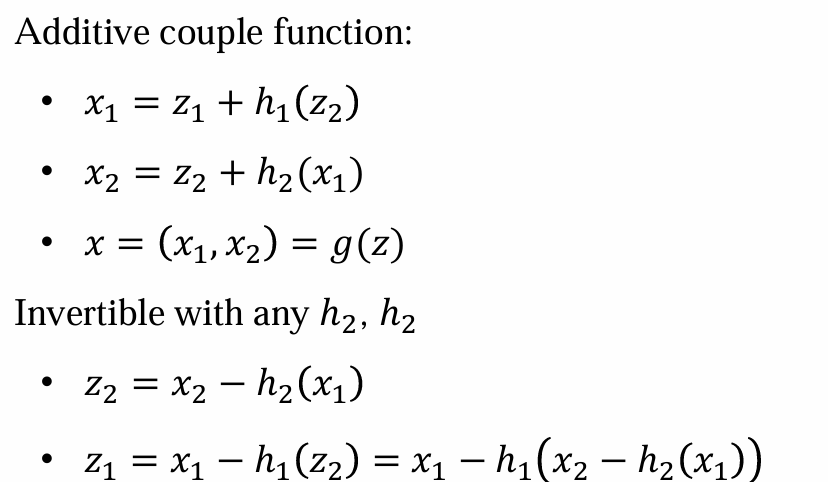
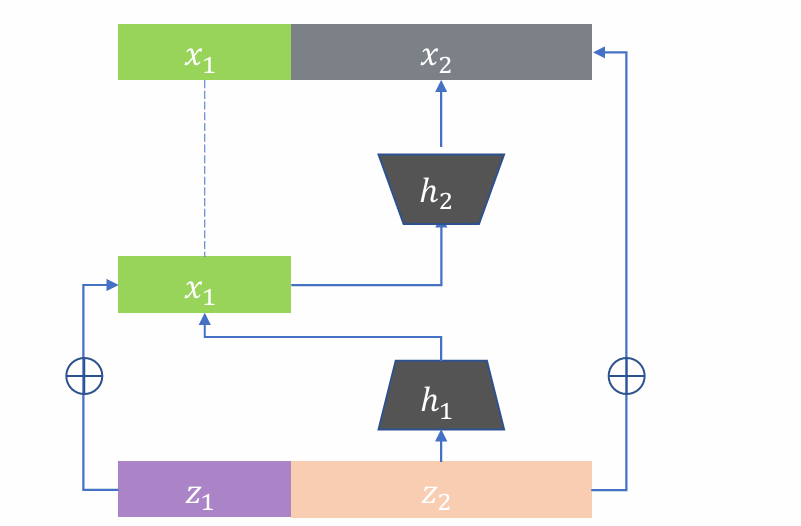
• h1,h2不加过多假设，否则导致雅各比矩阵难算，导致效率低

• 优点：能力很强，实践中实用；缺点：效率很低

---

Residual flow 2

• 𝑔(𝑧) = 𝑧 + ℎ(𝑧)，如果加以Lipchitz constraint:Lip(ℎ)<1，则可以保证g(z)可逆

• 优点：表达能力强，较为实用；缺点：效率很低

---