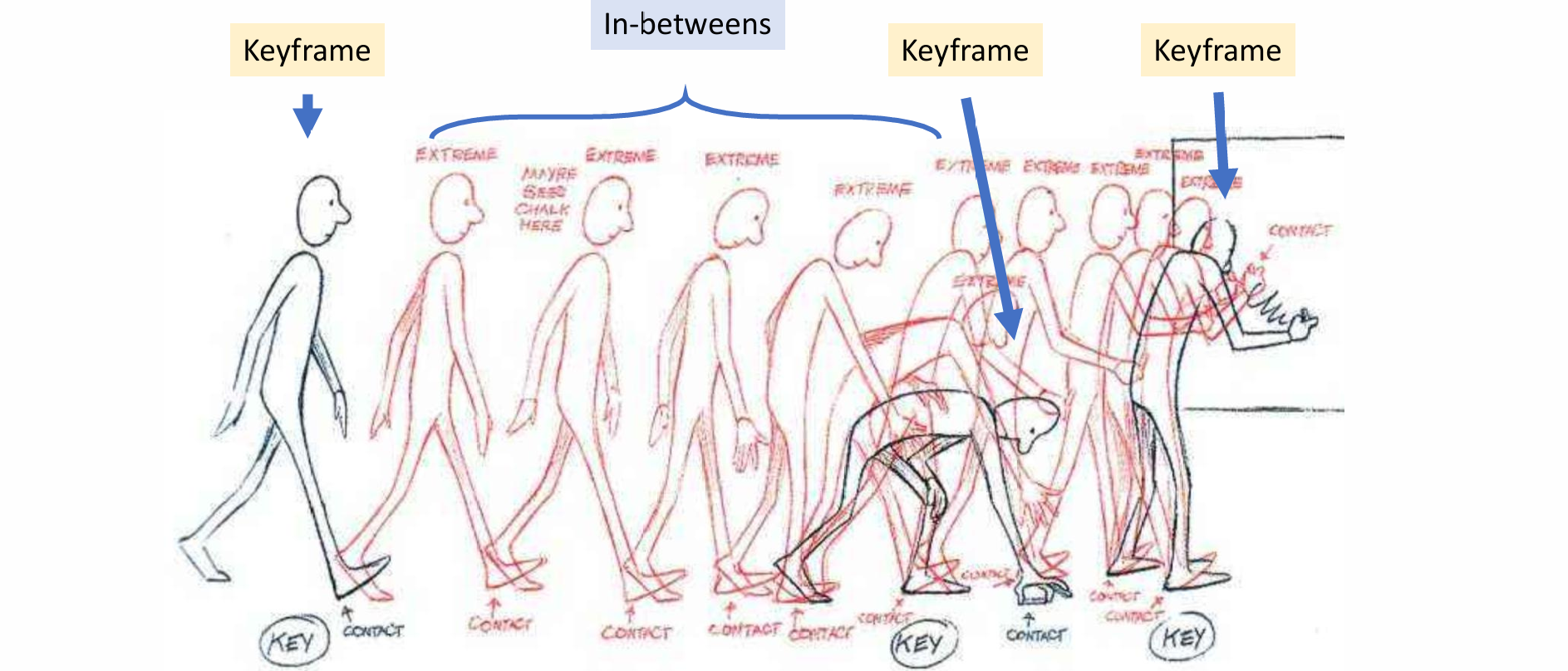
角色动画与运动仿真 04 Keyframe Animation
Keyframe Animation(关键帧动画)
- 动画流程:给出关键帧并通过算法补充中间的动画
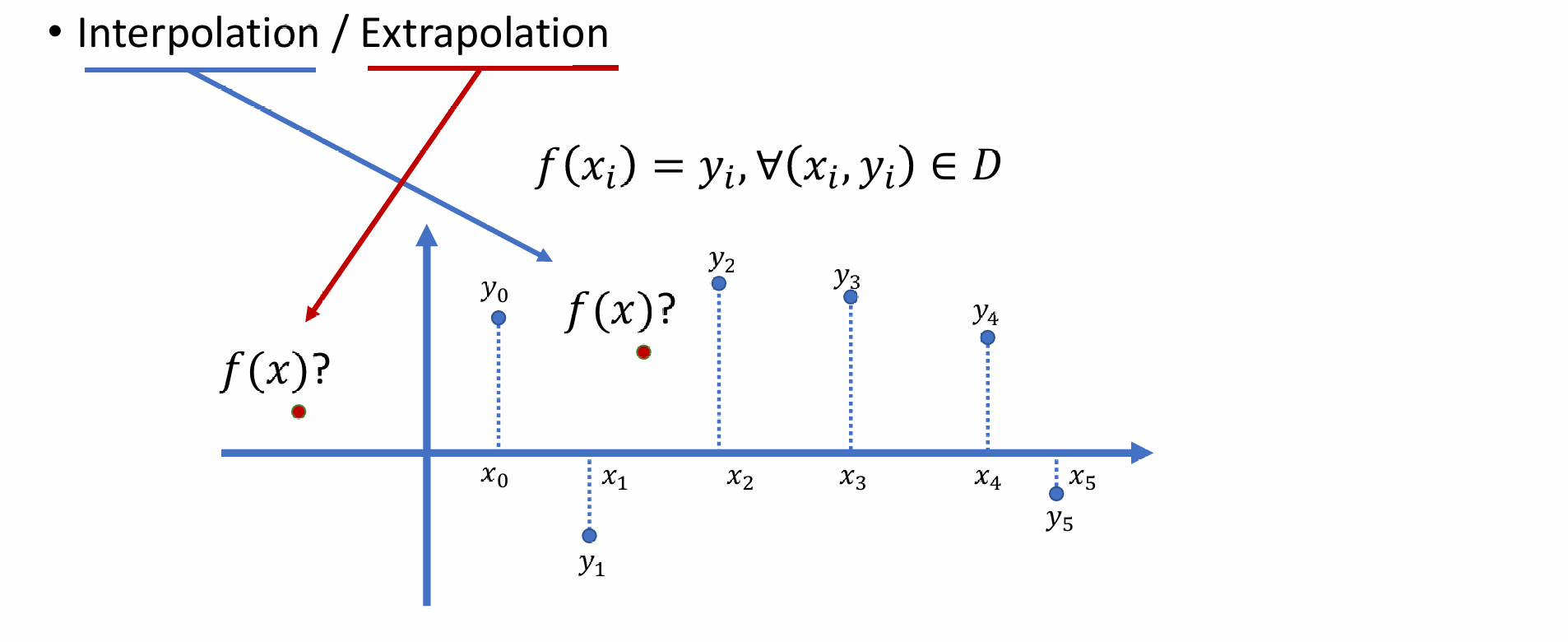
Interpolation
- 给定一系列关键点,计算关键点之间的点的值是多少——找f(x)映射:
- 关键点间的值:内插
- 关键点外的值:外插
Stepped Interpolation
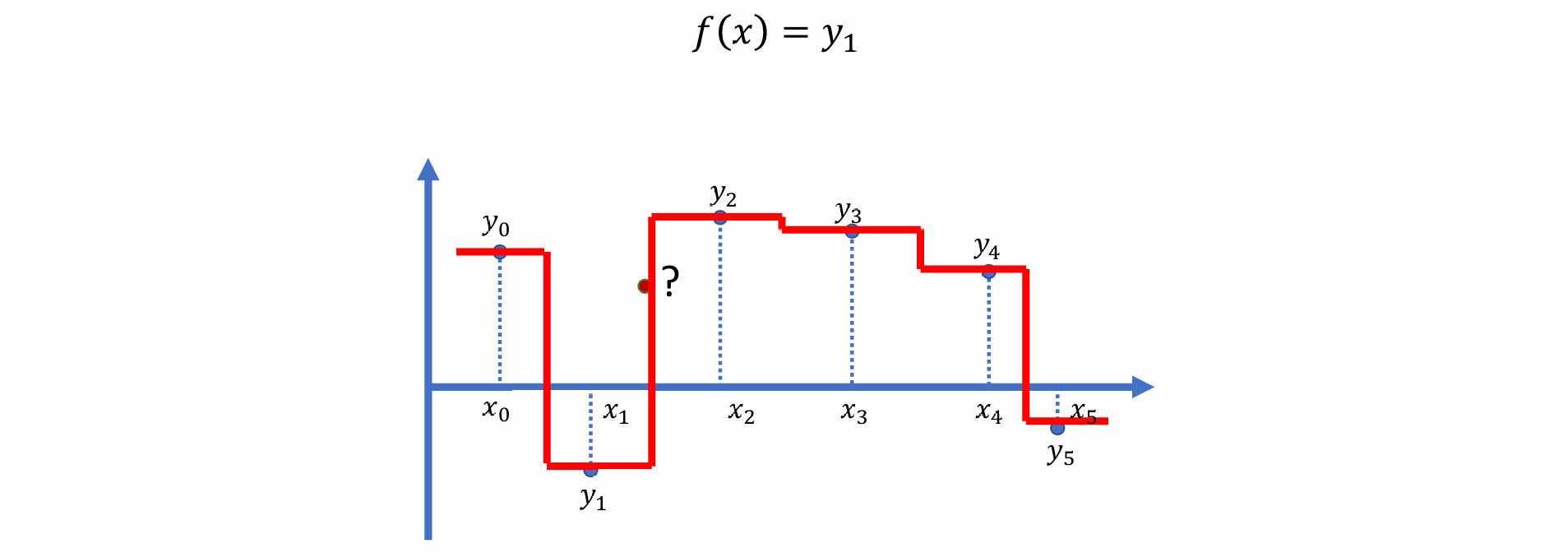
- 阶梯差值缺点:不够平滑,函数不连续
Linear Interpolation
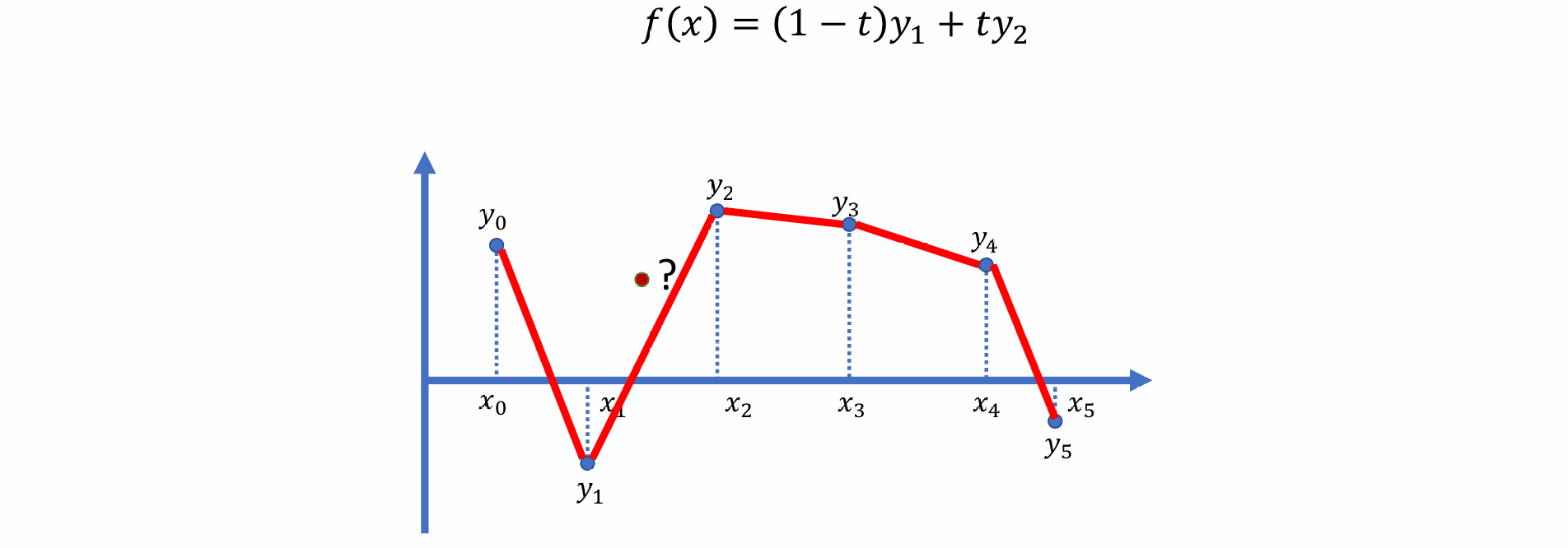
线性插值缺点:运动的时候可能突然改变速度(C1不连续),函数光滑性不够,C0连续
解决方法:需要非线性的插值
Polynomial Interpolation(多项式插值)
- 如果用单一的多项式进行插值,则有多少点就需要多少方程
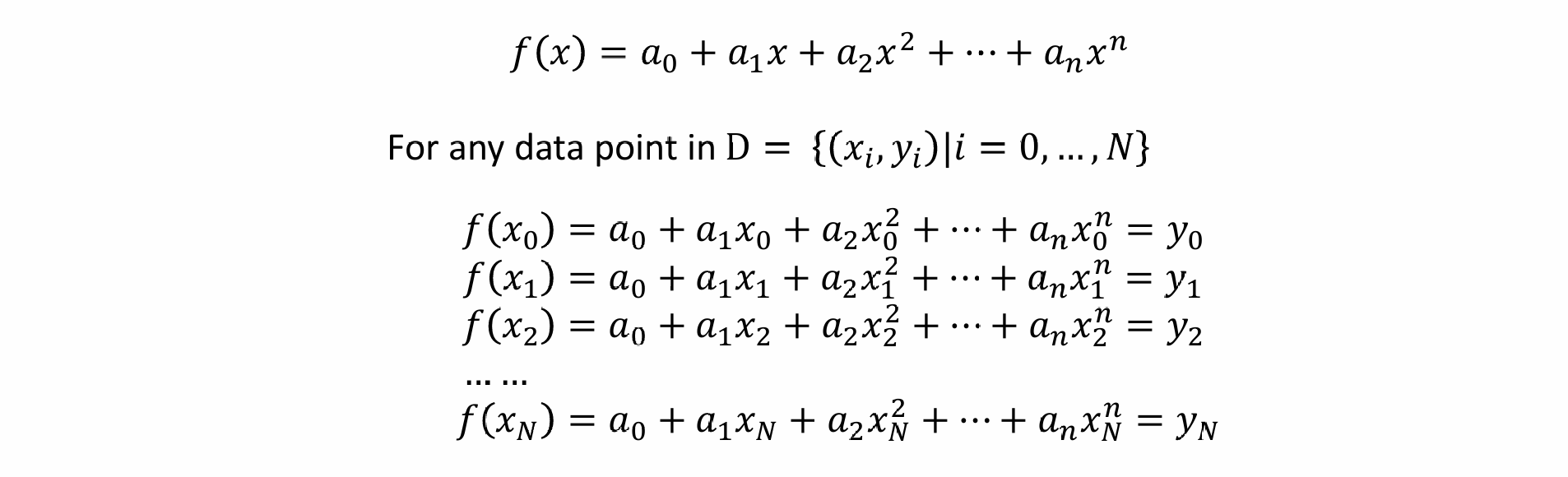
- 可以写成矩阵形式用待定系数法求解:
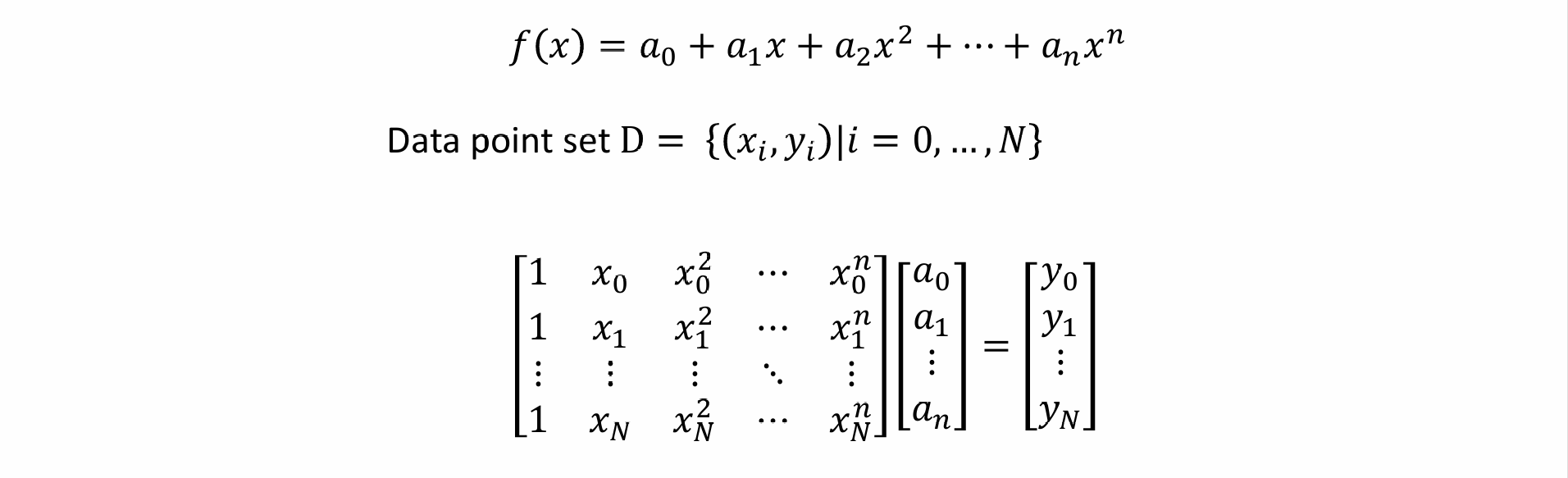
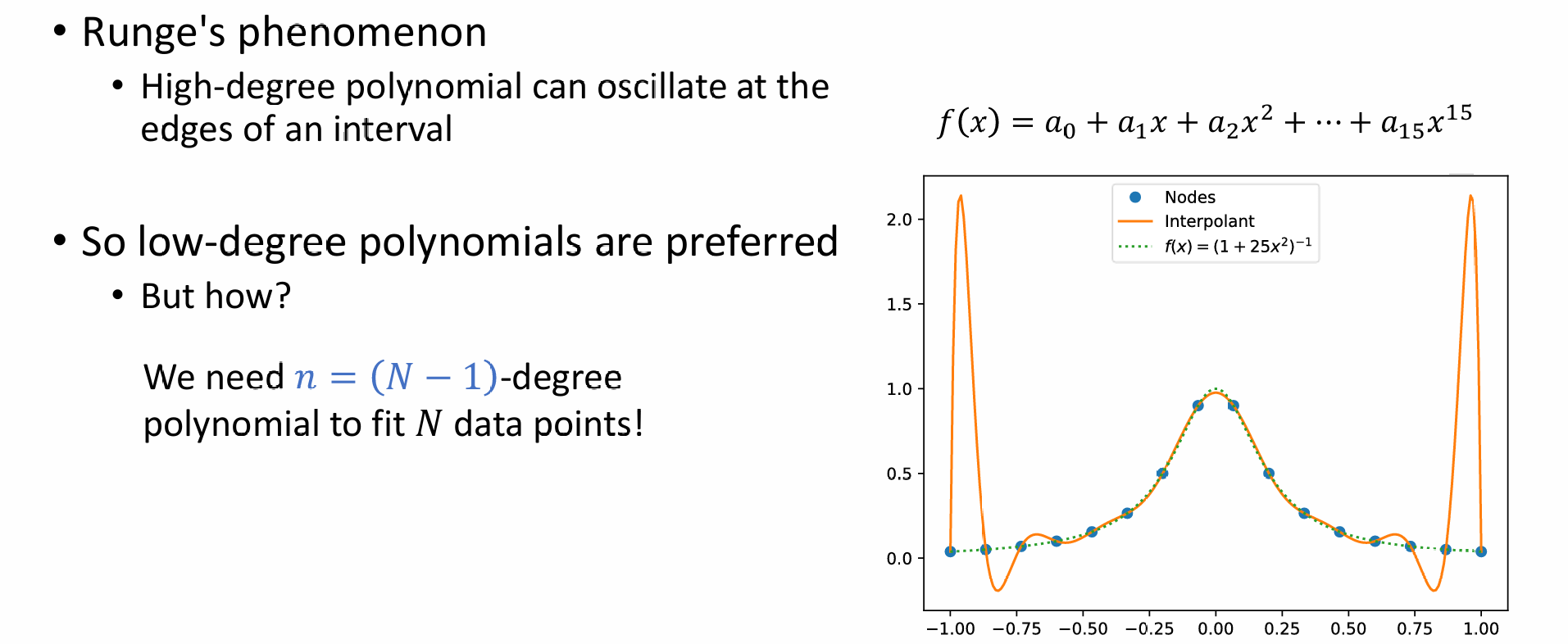
- 问题:高次项有龙格现象:高次项插值虽然插值过所有点,曲线光滑,但是抖动幅度很大
Spline Interpolation
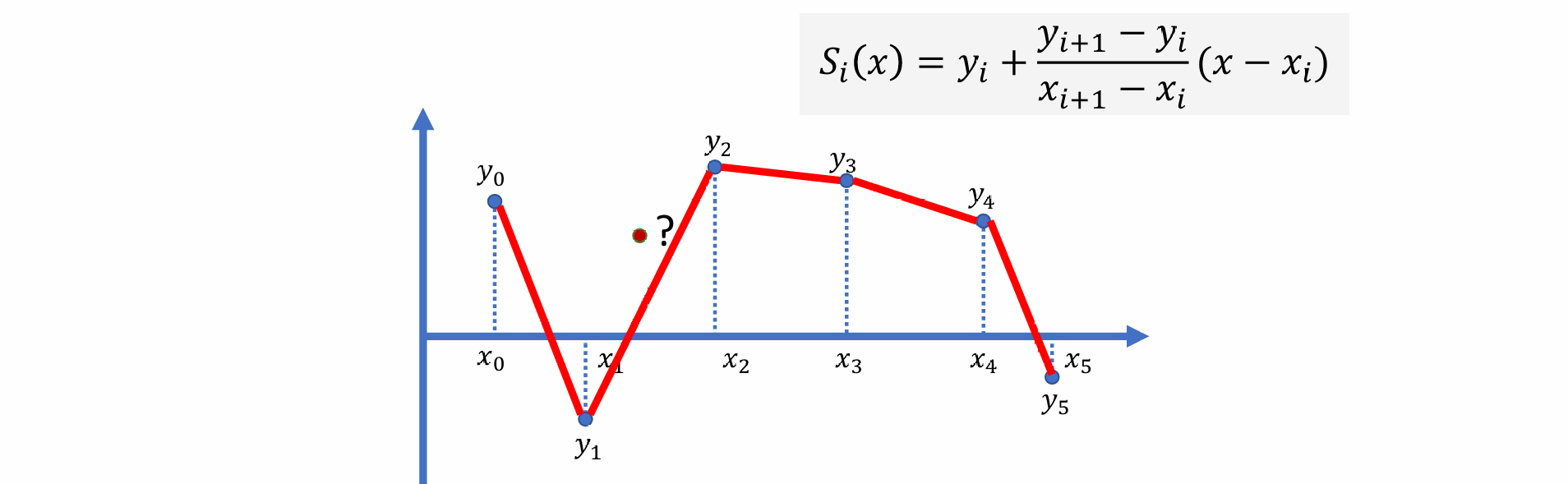
- 使用一阶的样条进行插值:类似于线性插值
- 常使用三次样条进行插值(Cubic Splines):
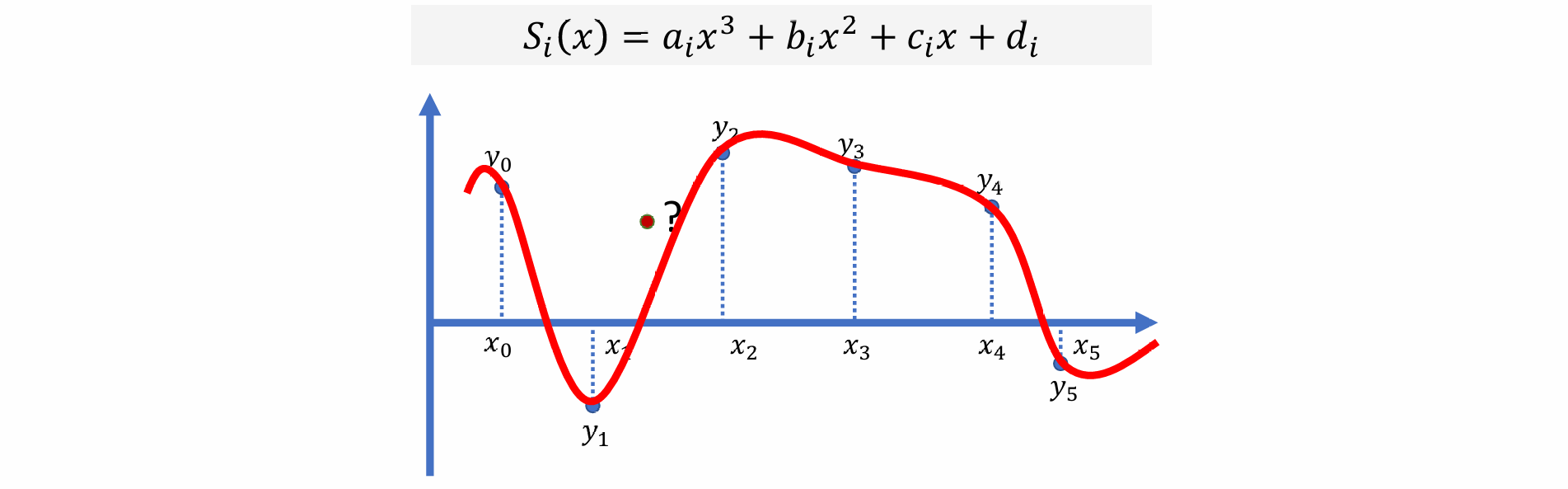
- 使用待定系数法求解:上例有 N 个段,4N 个未知参数,加入一些约束求解:
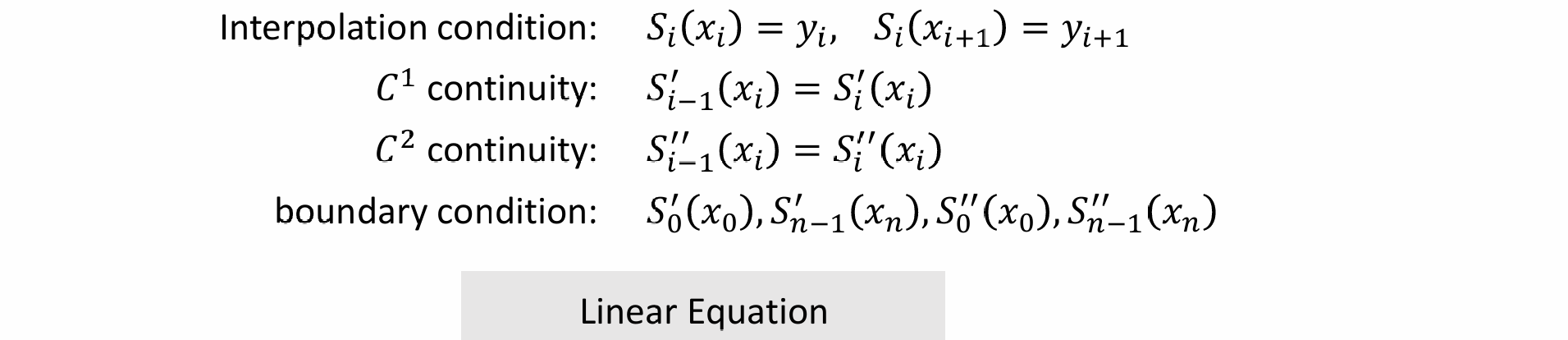
- 可以写成矩阵求解,但是这个矩阵很大,而且由于矩阵没有分块“牵一发而动全身”,每个参数都会产生全局影响
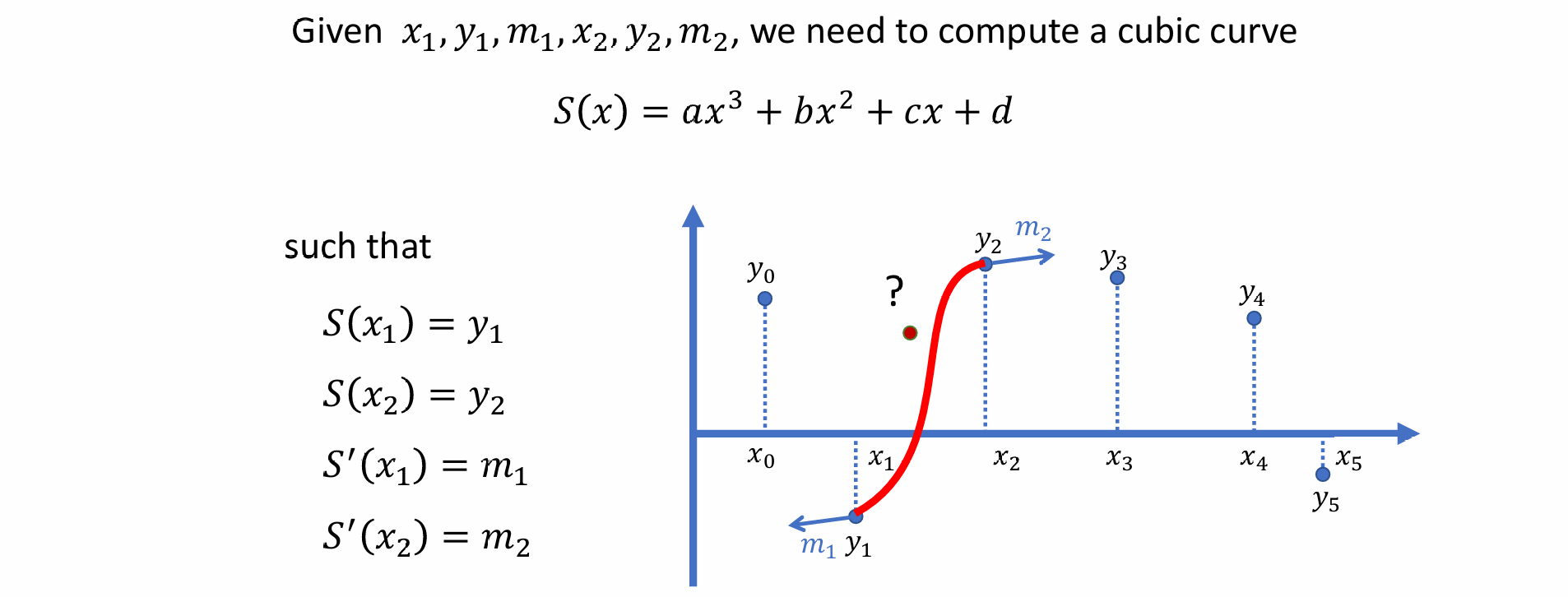
Cubic Hermite Splines
- 只保留第一项约束,去掉其他约束
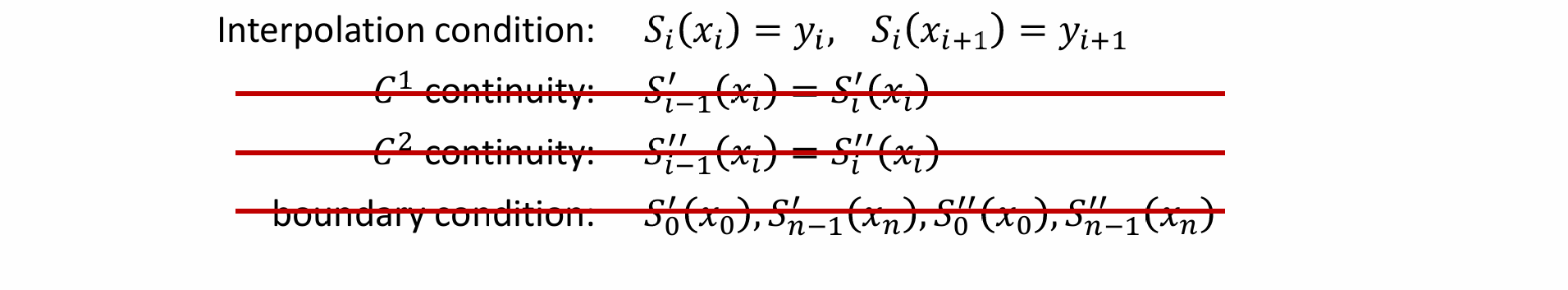
- 由于约束不够因而有多解,可以在端点位置加以约束从而用待定系数法求解:
- 端点的值必须等于给定值
- 端点的导数必须等于给定值
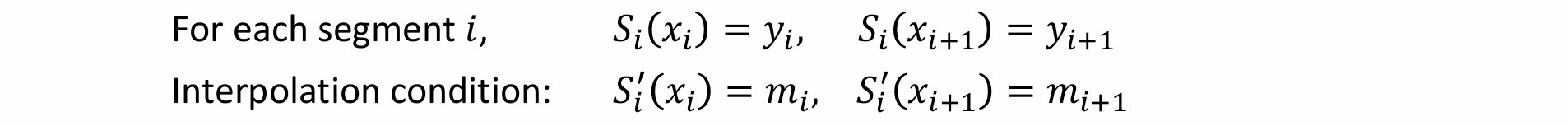
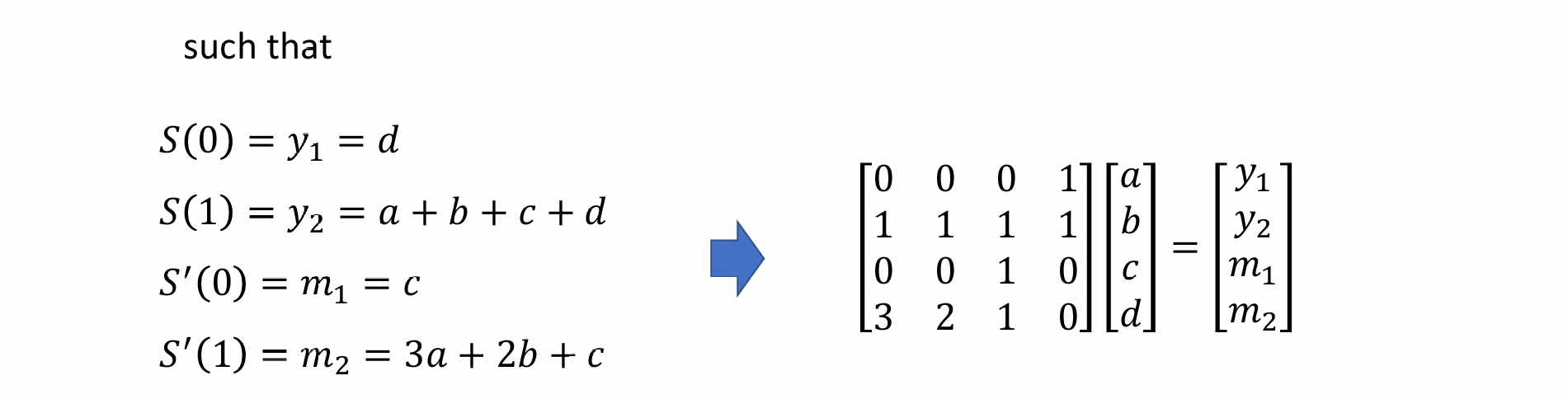
- 可以将其分解为两个矩阵,左矩阵是常数矩阵,右矩阵是需要给出的参数
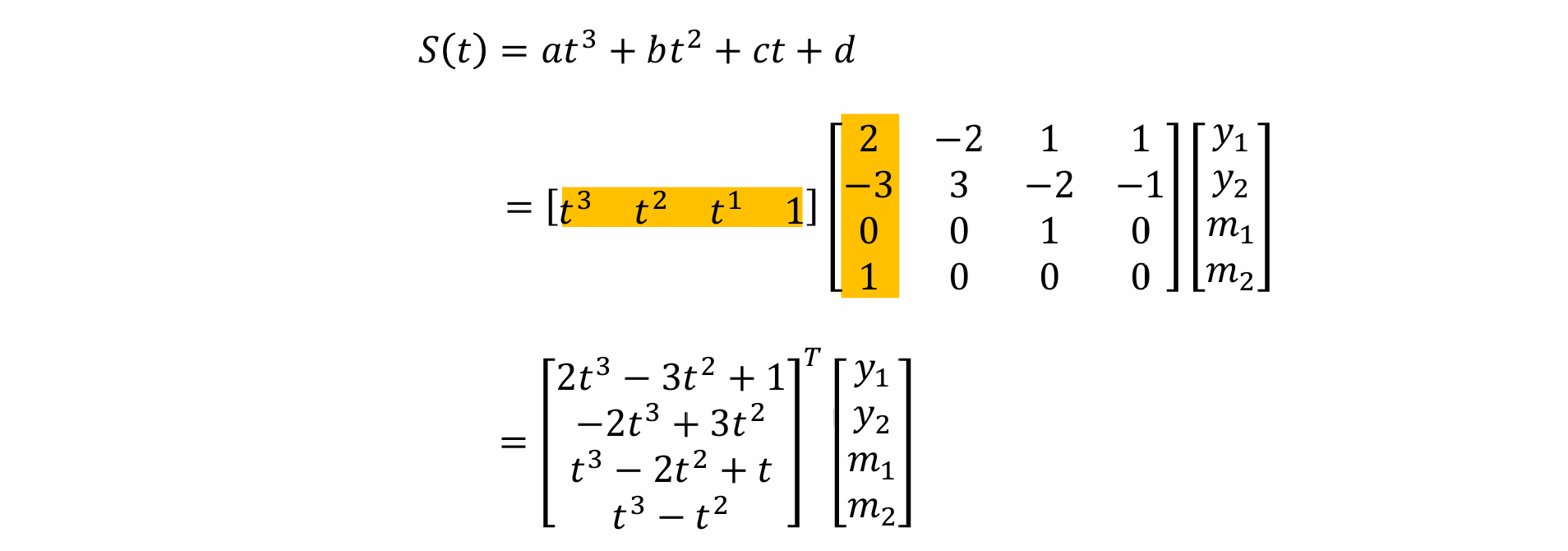
- 将这几个多项式命名为Hermite多项式,可得左矩阵是Hermite矩阵,右矩阵是需要给出的参数:
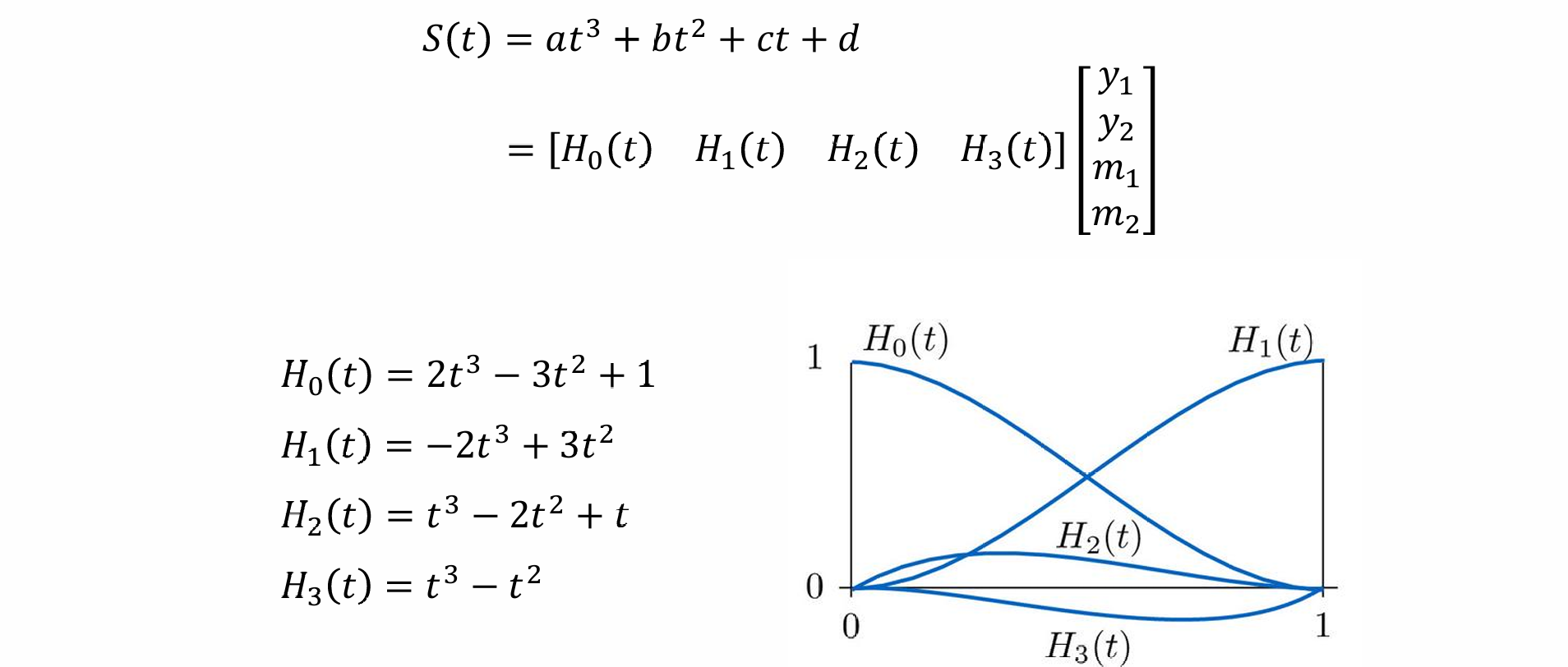
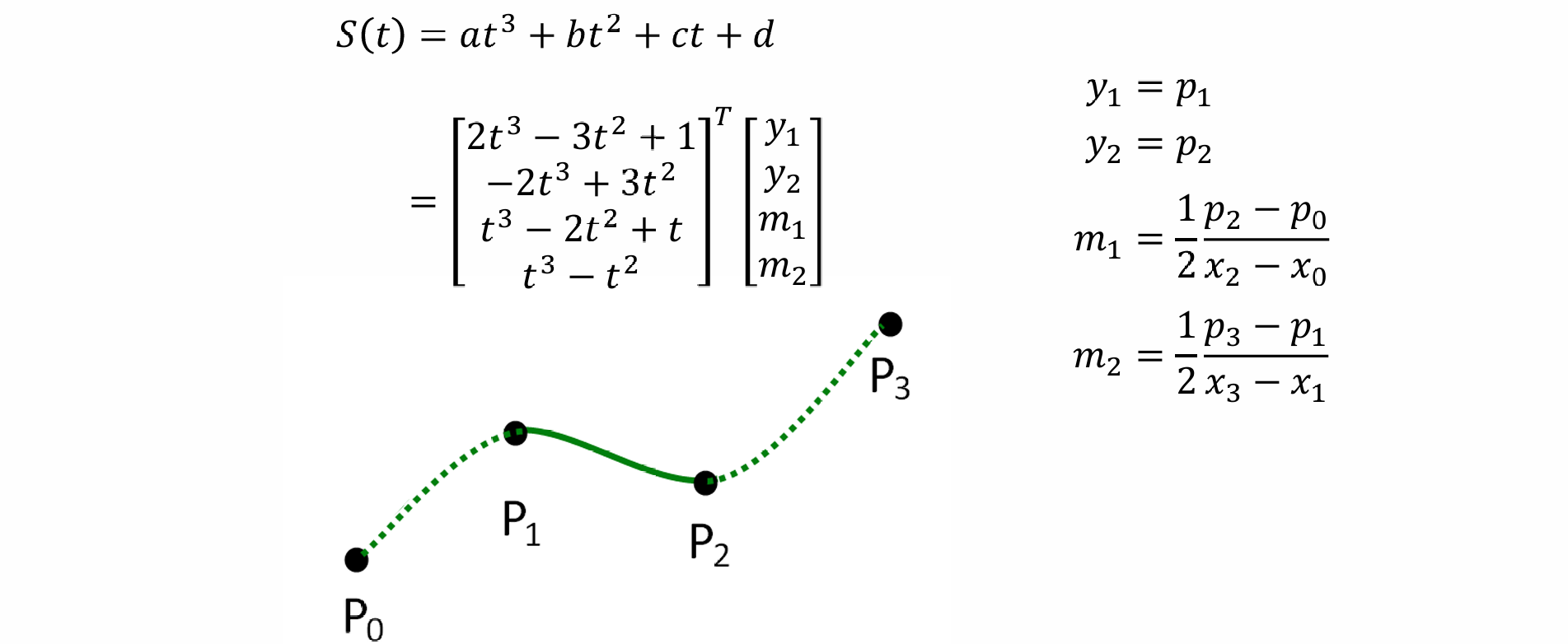
Catmull-RomSpline
- Cubic Hermite Splines需要给出端点的值和端点的导数的值,导数的值可以加以约束,如导数的值是端点间连线的导数值
Interpolation of Rotations
- 旋转表示的几种形式:
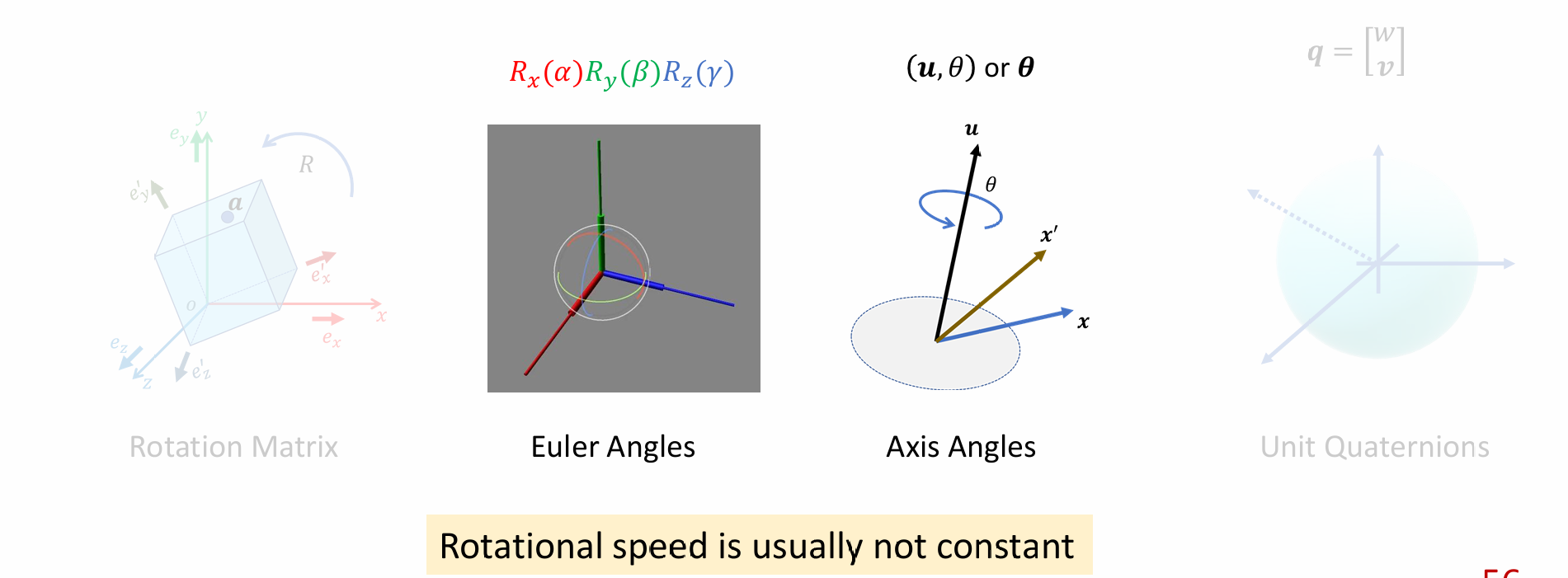
- 其中旋转矩阵无法插值,欧拉角、轴角表示和四元数可以进行插值,但是旋转速度不恒定
SLERP for Quaternions

Interpolation in a 2D space
- 在2D空间上插值得到曲面而非曲线
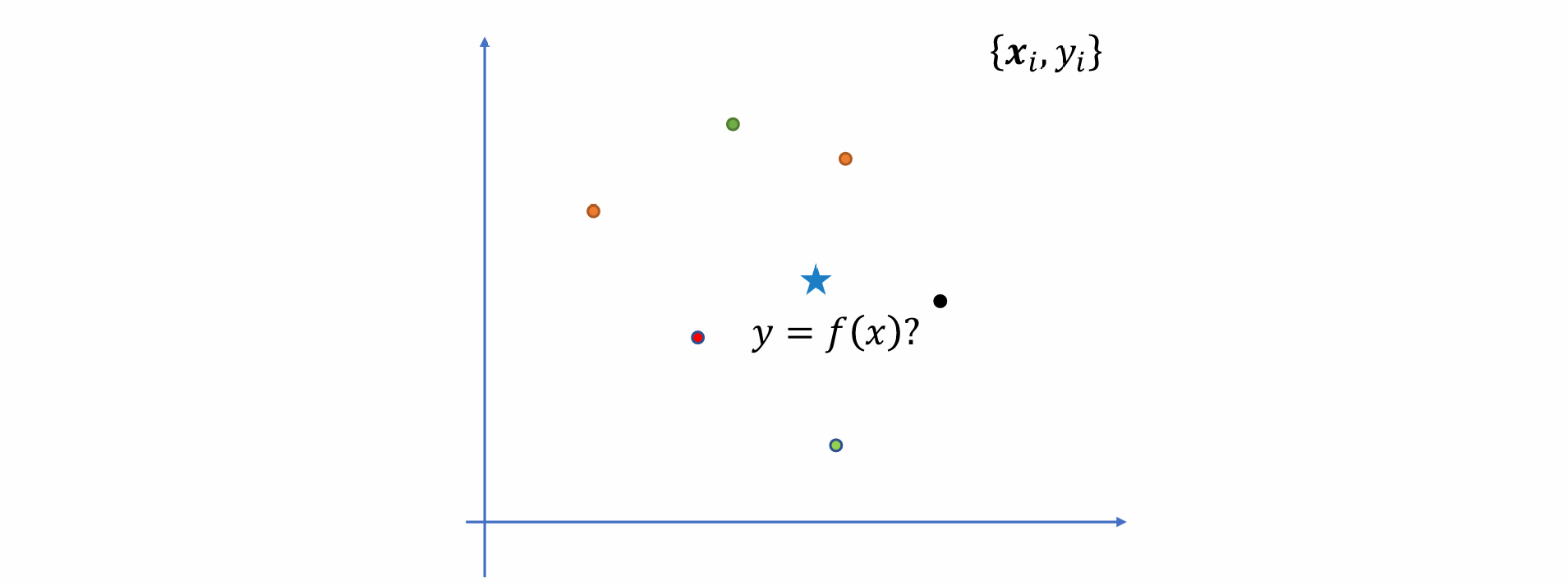
- 在2D平面上给出一系列点,用不同颜色表示,问题:给出一个新的点,求点的颜色
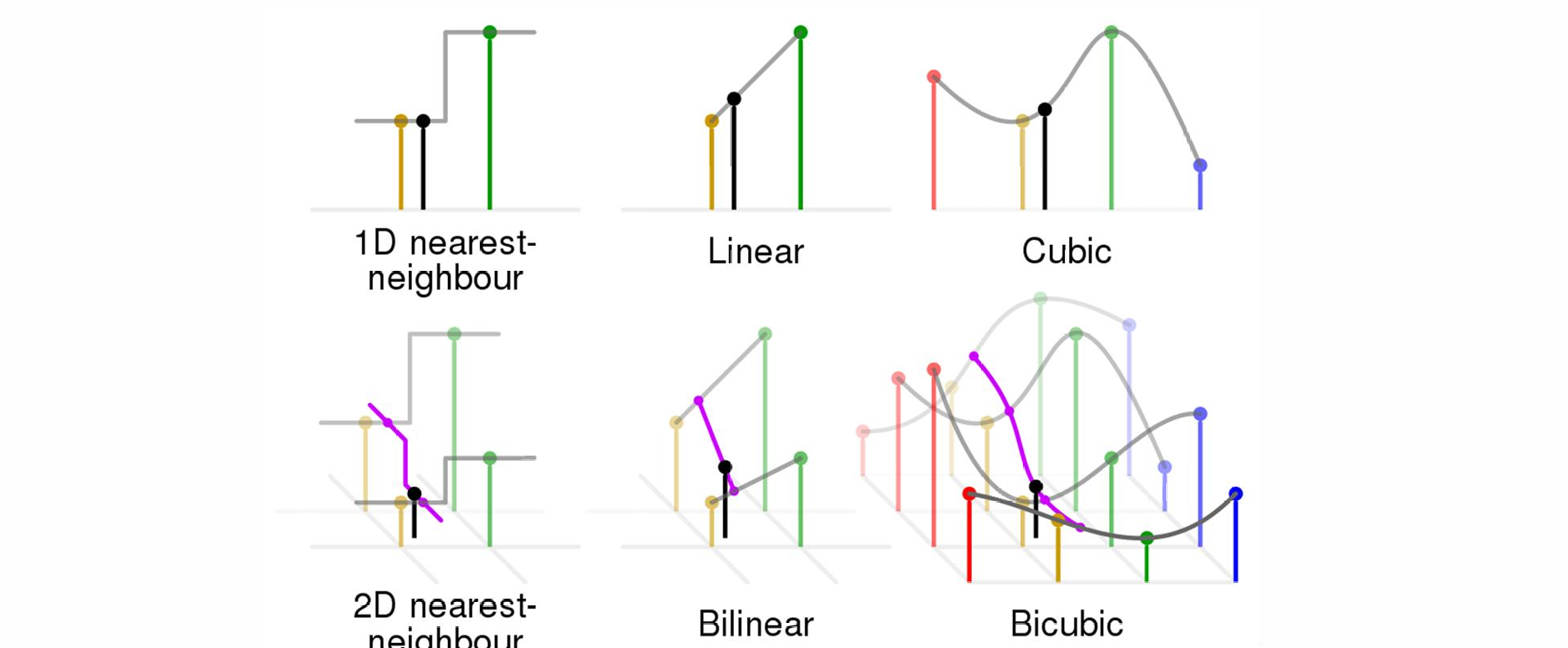
Bilinear Interpolation
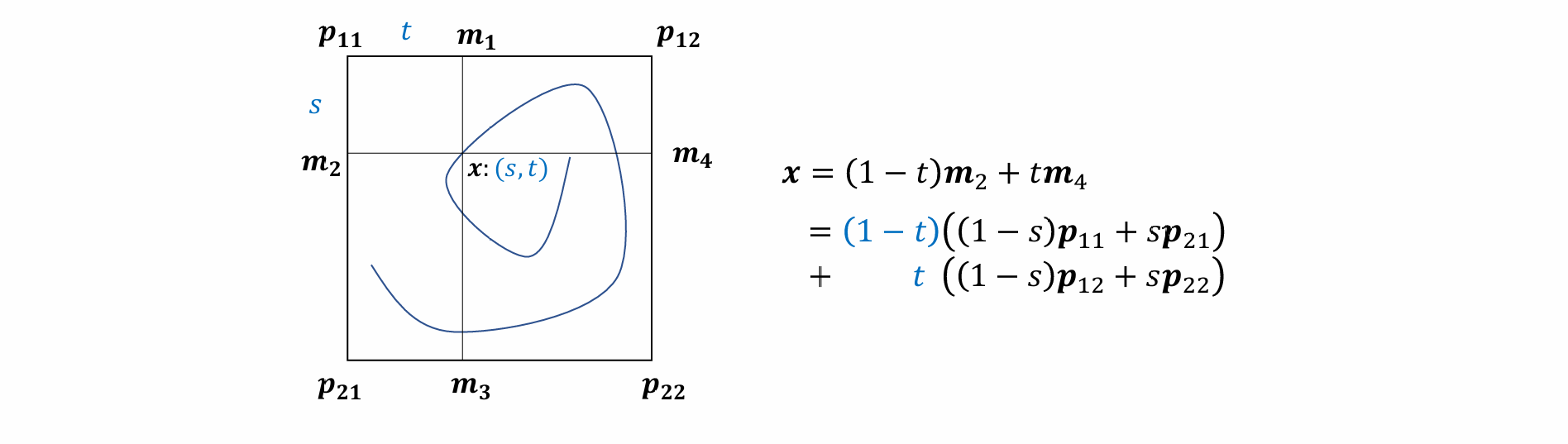
Barycentric Interpolation
- 通过重心坐标来求不同插值的权重
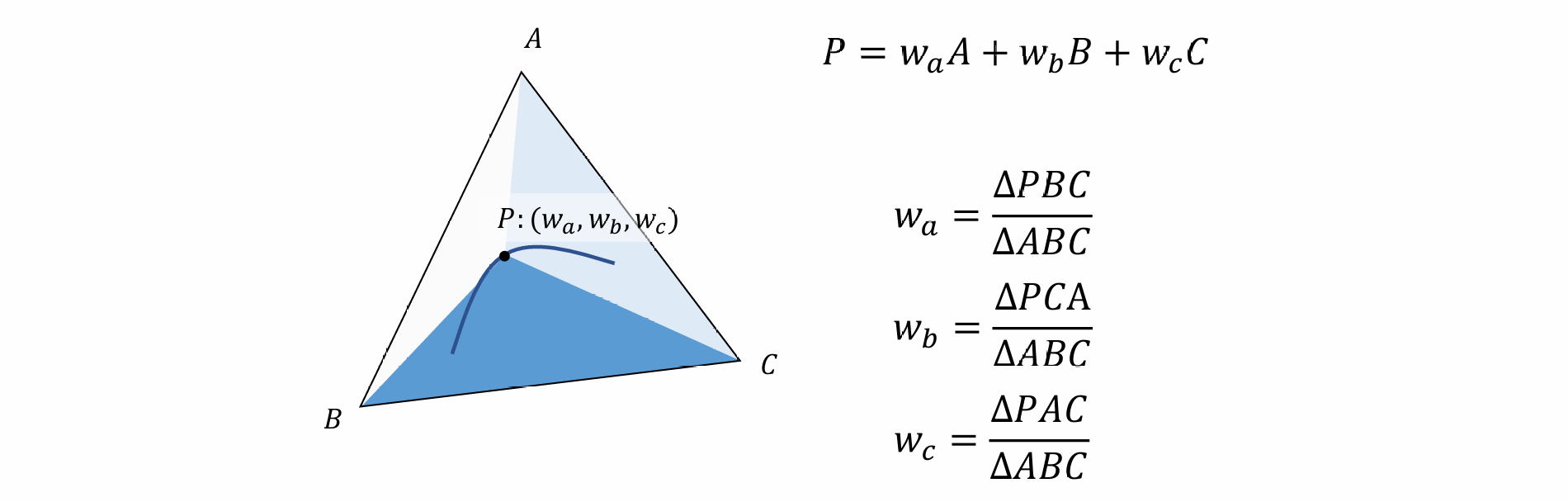
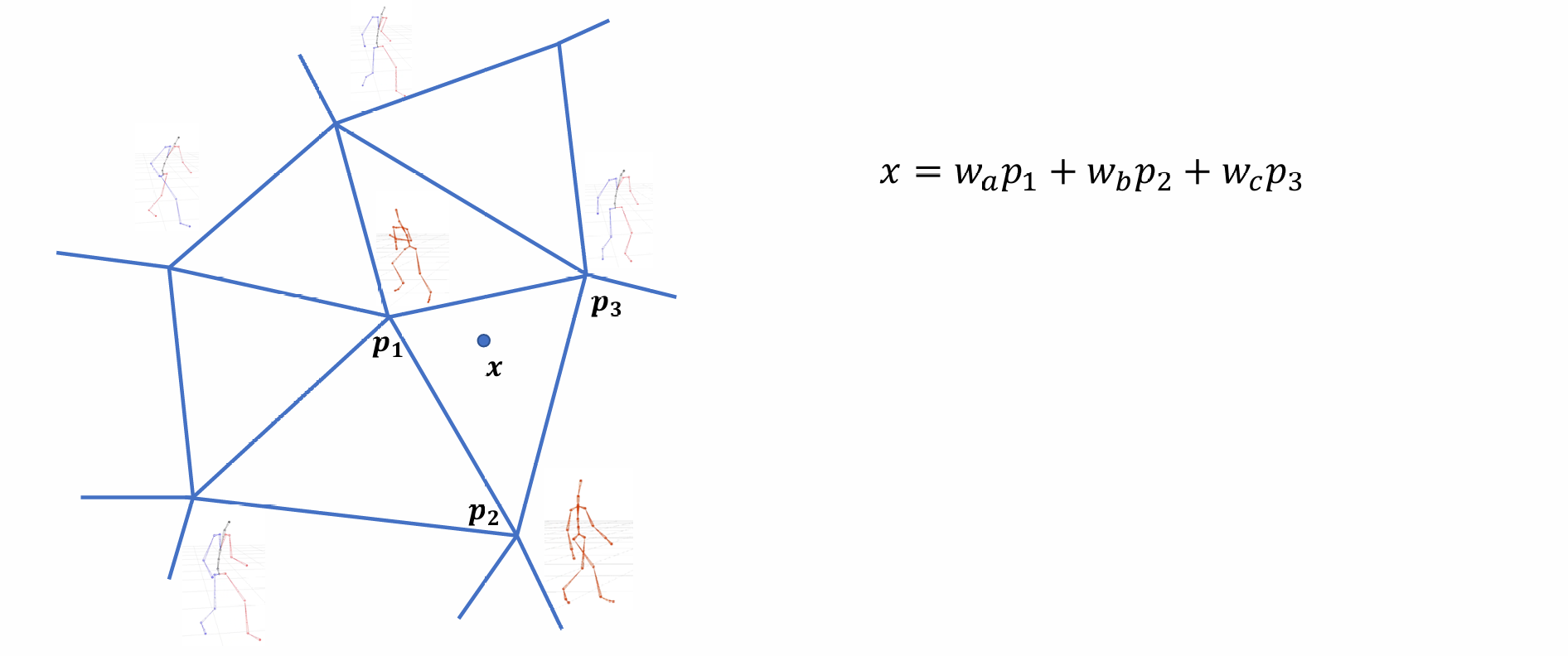
Blend Space
- 2D空间上插值的一个线性形式:可以先将平面中划分为三角形,再从三角形内部使用Barycentric Interpolation
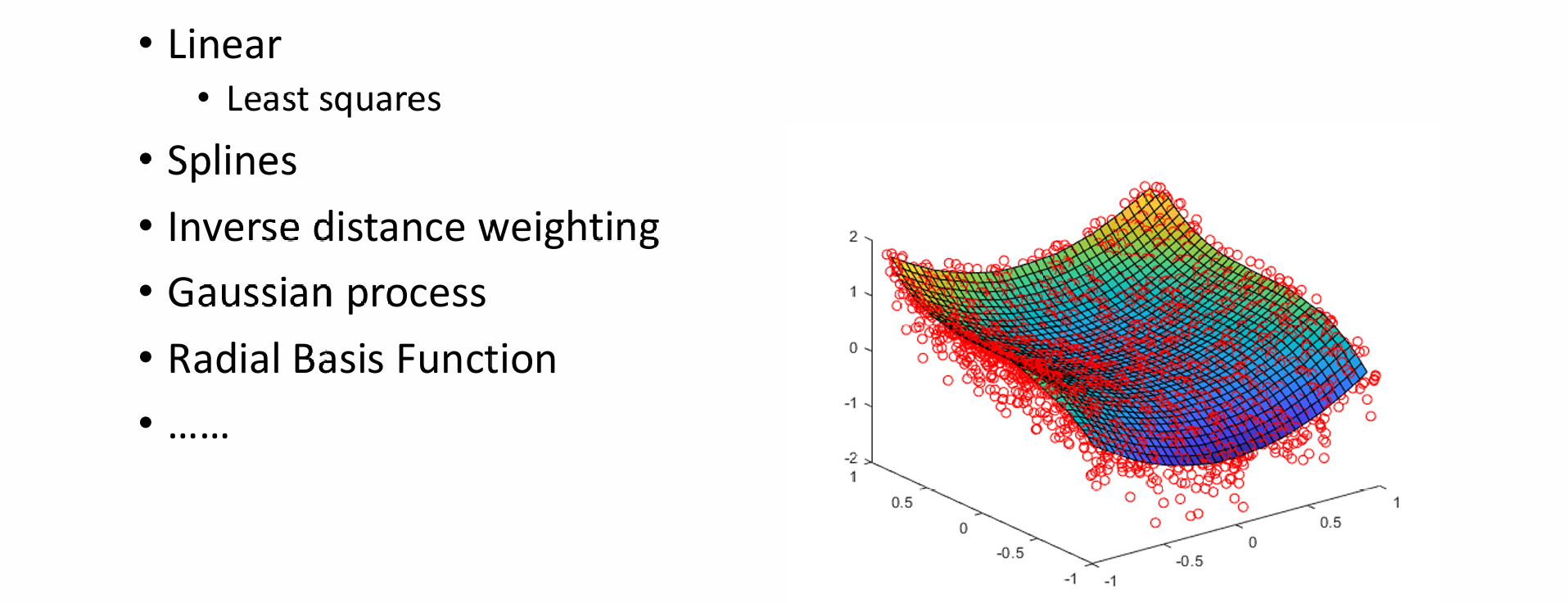
Scattered Data Interpolation
- 不希望线性插值,希望有非线性性质。若给出的点是随机散步在平面上,则可以使用散点插值,插值出形状
Radial Basis Function (RBF) Interpolation
- 镜像基函数法:每个点影响的大小与距离该点的距离相关,影响程度由镜像基函数决定
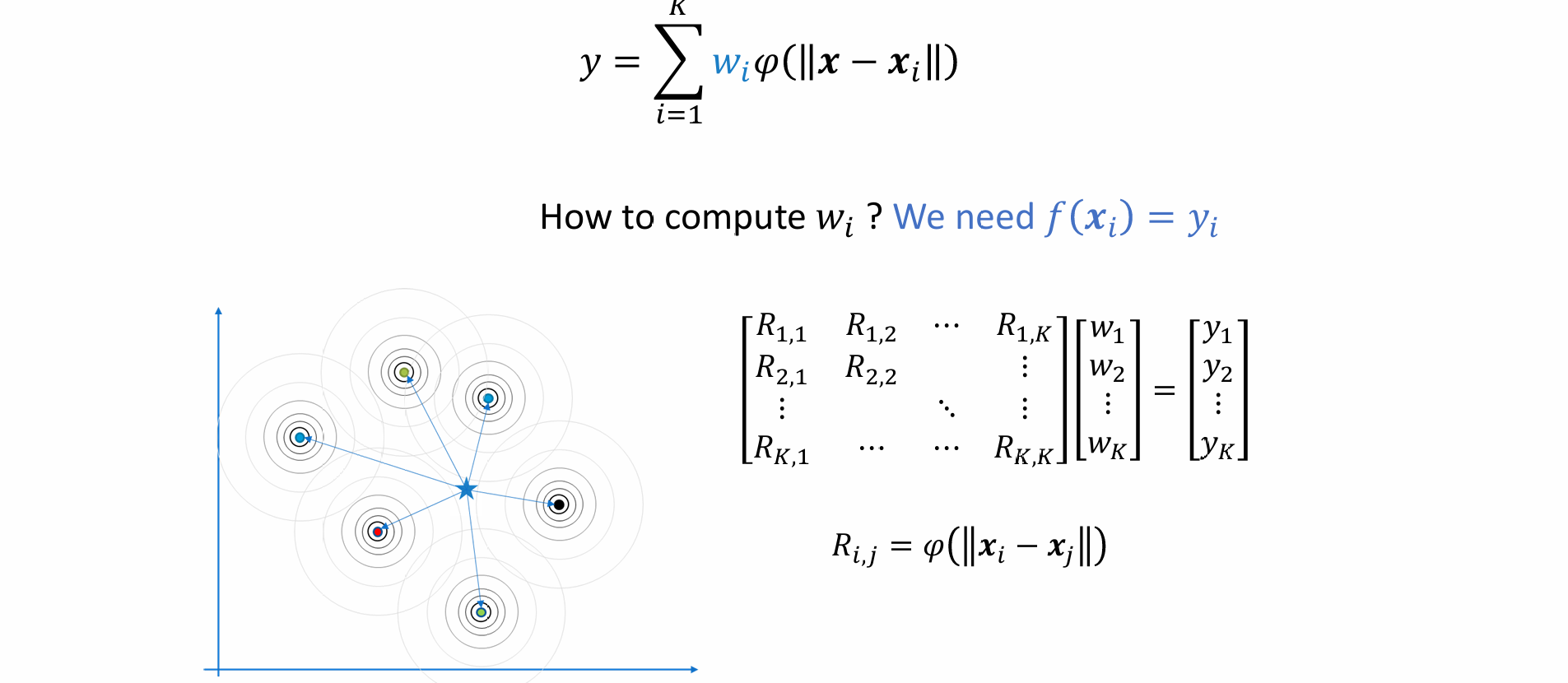
- 对每一个点可以算出一个距离矩阵,给出一个新的点后,则可算出该点到每个点的距离,再根据距离矩阵得到影响
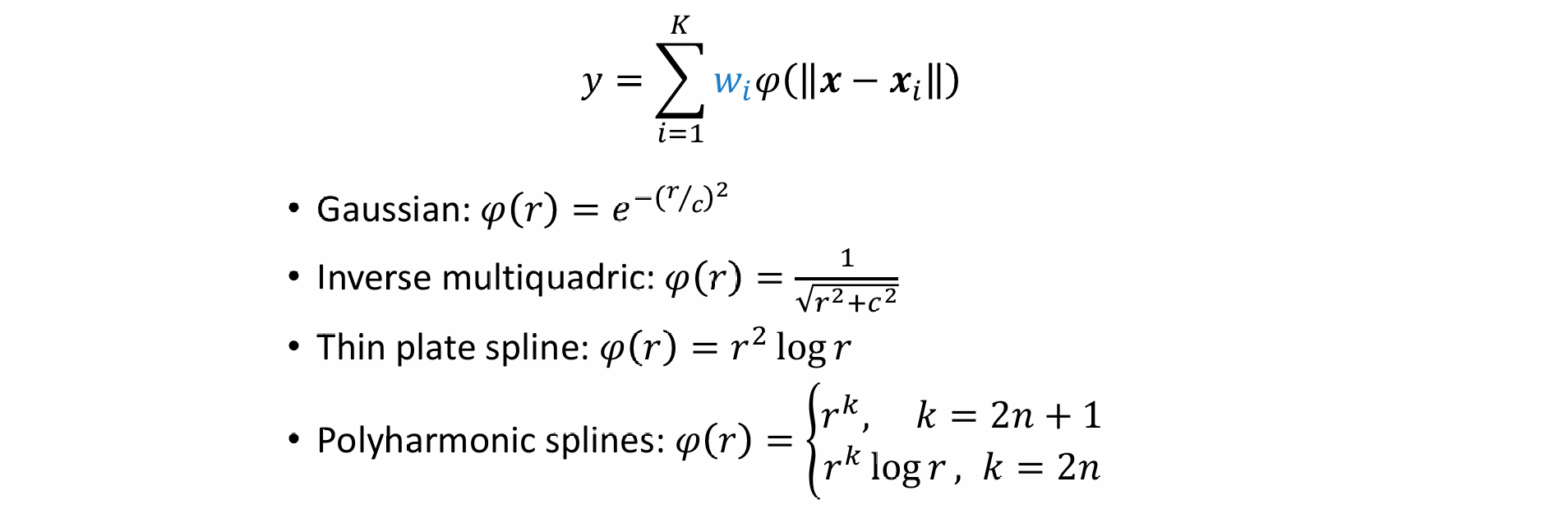
离点越近影响越大还是越小由镜像基函数影响
Precedure Animation:通过交互产生动画的过程


