主存储器和外存储器

计算机存储器是用来存储程序和数据的部件，主要有两种：
1. 主存储器(内存、主存)：
  1. 随机访问存储器(RAM)
  2. 高速缓存 ( cache )
  3. 视频存储器 ( video memory )
2. 外存储器(外存):
  1. 硬盘 (几百G - 几百T， 1012B )
  2. 磁带 (几个P， 1015B )
内存的优缺点:
1. 优点：访问速度快
2. 缺点：造价高，存储容量小，断电丢数据
CPU 直接与主存沟通，对存储在内存地址的数据进行访问时，所需要的时间可以看作是一个很小的常数
外存的优缺点：
1. 优点：价格低、信息不易失、便携性
2. 缺点：存取速度慢。一般的内存访问存取时间的单位是纳秒，外存一次访问时间则以毫秒或秒为数量级
为了解决存取速度的问题，外存上的数据通常采用分块存取的方式，外存空间被划分为长度固定的存储块，称为“页”，数据以页块作为单位进行存取

文件的组织和管理

文件是存储在外存上的数据结构，是由大量性质相同的记录组成的集合
记录：具有独立逻辑意义的数据块，是文件的基本数据单位
按照记录的类型，文件可以分为两类：
1. 操作系统的文件：一组连续的字符序列，没有明显的结构
2. 数据库文件：有结构的记录集合
按照记录信息长度，文件可以分为两类：
1. 定长文件：每一条记录均含有相同的信息长度
2. 不定长文件：记录不是相等长度的
按照关键码的个数，文件可以分为两类：
1. 单关键码文件：记录中只有一个标识关键码
2. 多关键码文件：记录中除了有一个主关键码以外还有若干个次关键码
文件的操作往往以记录为单位进行
文件的操作处理方式：
1. 实时：要求有较短的应答响应时间，尽可能快的完成检索或修改任务
2. 批量：允许较长时间反馈

文件组织

逻辑文件( logical file )：对高级程序语言的编程人员而言，连续的字节构成记录，记录构成逻辑文件
物理文件( physical file )：成块地分布在整个磁盘中
文件逻辑组织有三种形式：
1. 顺序结构的定长记录
2. 顺序结构的变长记录
3. 按关键码存取的记录
常见的物理组织结构：
1. 顺序结构——顺序文件
2. 计算寻址结构——散列文件
3. 带索引的结构——带索引文件
4. 倒排文件：倒排是一种特殊的索引
文件上的操作：
1. 检索：在文件中寻找满足一定条件的记录
2. 修改：是指对记录中某些数据值进行修改。若对关键码值进行修改，这相当于删除加插入
3. 插入：向文件中增加一个新记录
4. 排序：对指定好的数据项，按其值的大小把文件中的记录排成序列，较常用的是按关键码值的排序

C++ 的标准输入输出流类

C++语言以“流”的概念直接支持二进制序列文件结构，C++流的另一个主要用途是作为文件存取机制
文件流是以外存文件为输入/输出对象的数据流：每一个文件都有一个内存缓冲区与之对应：
1. 输入文件流：从外存文件流向内存的数据
2. 输出文件流：从内存流向外存文件的数据
标准输入输出流类：
1. istream 是通用输入流和其它输入流的基类，支持输入
2. ostream 是通用输出流和其它输出流的基类，支持输出
3. iostream 是通用输入输出流和其它输入输出流的基类，支持输入输出
3个用于文件操作的文件类：
1. ifstream 类，从 istream 类派生，支持从磁盘文件的输入
2. ofstream 类，从 ostream 类派生，支持向磁盘文件的输出
3. fstream 类，从 iostream 类派生，支持对磁盘文件的输入和输出
fstream类的主要成员函数：

#include <fstream.h> // fstream = ifstream + ofstream
void fstream::open(char*name, openmode mode); 
// 打开文件
fstream::read(char*ptr, int numbytes); // 从文件当前位置读入字节
fstream::write(char*ptr, int numbtyes); // 向文件当前位置写入字节
// seekg和seekp：在文件中移动当前位置
// 以便在文件中的任何位置读出或写入字节
fstream::seekg(int pos); // 输入时用于设置读取位置
fstream::seekg(int pos, ios::curr);
fstream::seekp(int pos); // 设置输出时的写入位置
fstream::seekp(int pos, ios::end);
void fstream::close(); // 处理结束后关闭文件

文件常见的三个基本操作：
1. 文件指针定位
2. 在当前文件指针位置读取
3. 向当前文件指针位置写入
缓冲区和缓冲池：
1. 目的：减少磁盘访问次数
2. 方法：缓冲 ( buffering ) 或缓存( caching )
存储在一个缓冲区中的信息经常称为一页( page )，往往是一次 I/O 的量。缓冲区合起来称为缓冲池( buffer pool )
新的页块申请缓冲区时，把最近最不可能被再次引用的缓冲区释放来存放新页：
1. “先进先出”( FIFO )
2. “最不频繁使用”( LFU )
3. “最近最少使用”( LRU )

外排序

外排序：对外存设备上(文件)的排序技术
待排的文件非常大，内存放不下，只能分段处理
通常由两个相对独立的阶段组成：
1. 文件形成尽可能长的初始顺串（run ），作为待归并段，将来处理
2. 处理顺串，最后形成对整个数据文件的排列文件
外排序的时间组成：
1. 产生初始顺串的内排序所需时间
2. 初始化顺串和归并过程所需的读写（I/O）时间
3. 内部归并所需要的时间
减少外存信息的读写（I/O）次数是提高外部排序效率的关键

置换选择排序

目的：将文件生成若干初始顺串（顺串越长越好，个数越少越好）
实现：借助在RAM中的堆来完成

算法的处理过程：
1. 从输入文件读取一定数量的记录进入输入缓冲区
2. 向内存工作区中放入待排序的记录并且进行排序
3. 记录被处理后，写到输出缓冲区
4. 当输出缓冲区写满时，把整个缓冲区写回到外存文件
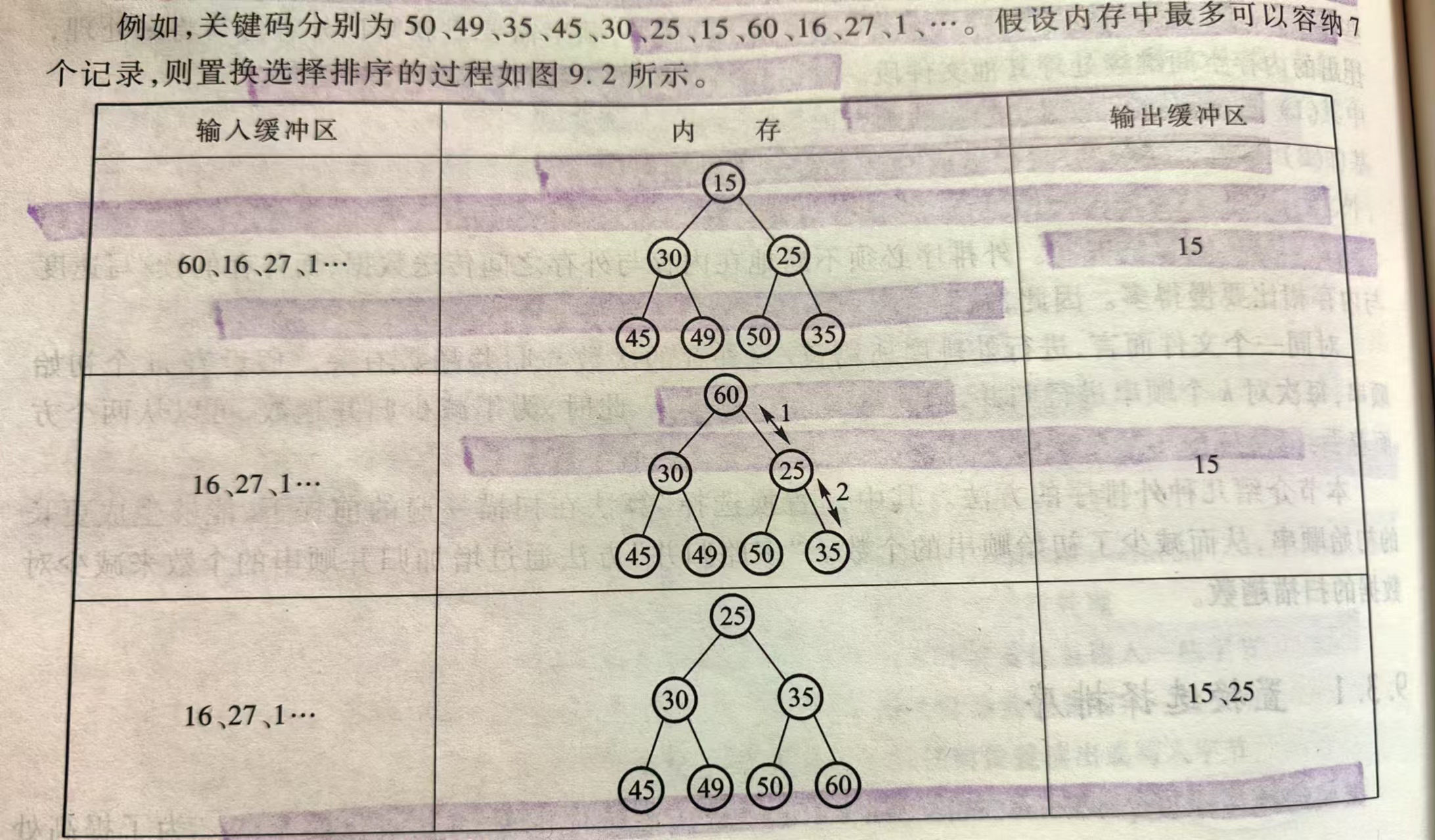
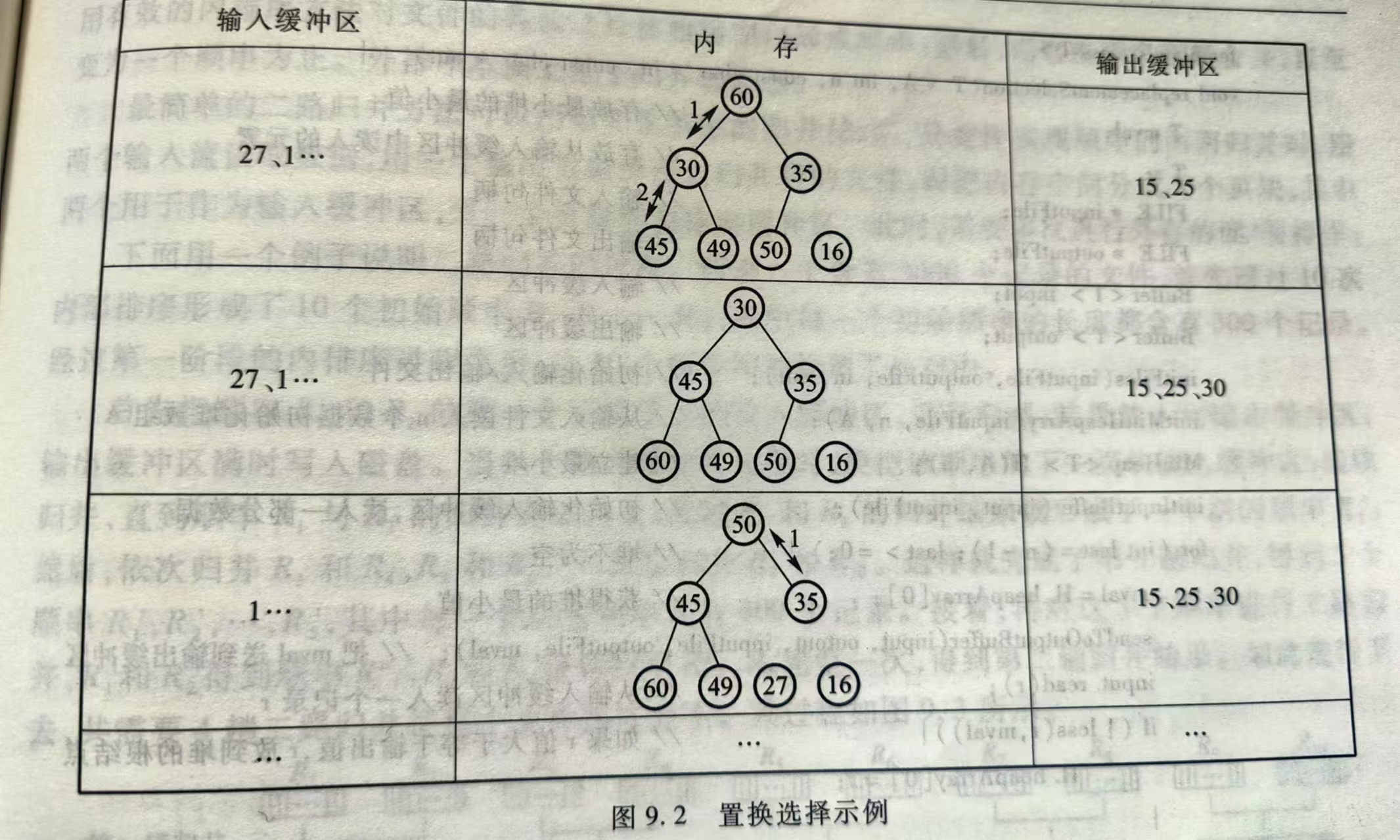
置换选择算法产生一个顺串的流程：
1. 初始化最小堆：目的是提高RAM中排序的效率
  1. 从缓冲区读M个记录放到数组RAM中
  2. 设置堆尾标志：LAST ＝ M － 1
  3. 建立一个最小值堆
2. 重复以下步骤，直至堆空（结束条件）（即LAST < 0）
  1. 把具有最小关键码值的记录(根结点)送到输出缓冲区
  2. 设R是输入缓冲区中的下一条记录
    1. 如果R的关键码不小于刚输出的关键码值，则把R放到根结点
    2. 否则，使用数组中LAST位置的记录代替根结点，然后把R放到LAST位置（等待下一顺串处理），设置LAST ＝ LAST-1
  3. 重新排列堆，筛出根结点

// 置换选择算法的实现
// 模板参数 Elem 代表数组中每一个元素的类型
// A 是从外存读入 n 个元素后所存放的数组
// in 和 out 分别是输入和输出文件名
template <class Elem>
void replacementSelection(Elem * A, int n, const char * in, const char * out) 
{ 
    Elem mval; // 存放最小值堆的最小值
    Elem r; // 存放从输入缓冲区中读入的元素
    FILE * inputFile; // 输入、输出文件句柄
    FILE * outputFile;
    Buffer<Elem> input; // 输入、输出buffer
    Buffer<Elem> output; // 初始化输入输出文件
    initFiles(inputFile, outputFile, in, out);
    initMinHeapArry(inputFile, n, A); // 建堆
    MinHeap<Elem> H(A, n, n);
    initInputBuffer(input, inputFile);
    for(int last = (n-1); last >= 0;)
    {
        mval = H.heapArray[0]; // 最小值
        sendToOutputBuffer(input, output, inputFile, outputFile, mval);
        input.read(r); // 从输入缓冲区读入一个记录
        if (!less(r, mval))
            H.heapArray[0] = r; // r放到根结点
        else 
        {   // last记录代替根结点，r放到last位置
            H.heapArray[0] = H.heapArray[last];
            H.heapArray[last] = r;
            H.setSize(last--);
        }
            H.SiftDown(0); // 调整根结点
    } // for
    endUp(output, inputFile, outputFile);
}

堆的大小 M，算法得到的顺串长度并不相等
最好的情况下，例如输入为正序，有可能一次就把整个文件生成为一个顺串
平均情况下，置换选择排序算法可以形成长度为2M 的顺串

二路外排序

归并原理：把第一阶段所生成的顺串加以合并(例如通过若干次二路合并)，直至变为一个顺串为止，即形成一个已排序的文件
外排序实现两两归并时，用两个输入流读取数据，用一个输出数据流建立归并后的文件，即把内存空间分成三个页块。其中两个用于作为输入缓冲区，另一个页块作为输出缓冲区
例如有10个初始顺串R1,…,R10
1. 首先把顺串R1,R2的第一个页块读入到缓冲区，进行归并，结果放入到输出缓冲区，输出缓冲区满时写入磁盘
2. 当一个输入缓冲区为空时，便把顺串的下一个页块读入到缓冲区，继续归并，直到顺串R1,R2的归并完全完成为止
3. 此时R1,R2的归并结果就形成了一个新的顺串R1’,然后一次归并R3和R4,R5和R6…完成第一趟归并
4. 完成第二趟归并,第三趟归并直到归并成一个
为一个待排文件创建尽可能大的初始顺串，可以大大减少扫描遍数和外存读写次数
归并顺序的安排也能影响读写次数，把初始顺串长度作为权，其实质就是 Huffman 树最优化问题

多路归并——选择树

k路归并：每次将k个顺串合并成一个排好序的顺串
目的：提高在k个归并串的当前值中找到最小值的效率
对m个初始顺串进行k路归并时，归并趟数为[logk(m)]，增加每次归并的顺串数量k可以减少归并趟数
内部归并进行的总比较次数为：[log2(m)]*(n-1)，内部比较次数与k无关，不随k的增加而增加
选择树是完全二叉树，通常采用顺序结构。选择树又称竞赛树，反映了一种淘汰赛的结果，分为：赢者树和败者树

嬴者树

叶子结点用数组 L[1..n]表示：代表各顺串在合并过程中的当前记录
分支结点用数组 B[1..n-1]表示：每个分支结点代表其两个儿子结点中的赢者(关键码值较小的)所对应数组L的索引
根结点 B[1] 是树中的最终赢者的索引，即为下一个要输出的记录结点
如果一个选手L[i]的分数值改变了，可以很容易地修改这棵赢者树：只需要沿着从L[i]到根结点的路径修改二叉树，而不必改变其它比赛的结果
为了使得过程更高效，如果沿到树根结点路径上的某一场比赛结果没有改变，则不需要再进行其祖先结点的比赛。这样修改次数再0~log2(n)之间
赢者树与数组的对应关系：

败者树

败方树是赢者树的一种变体
在败方树中，用父结点记录其左右子结点进行比赛的败者，而让获胜者去参加更高阶段的比赛
新增根结点B[0]，来记录整个比赛的全局胜者
败方树是为了简化重构过程，树结构未变

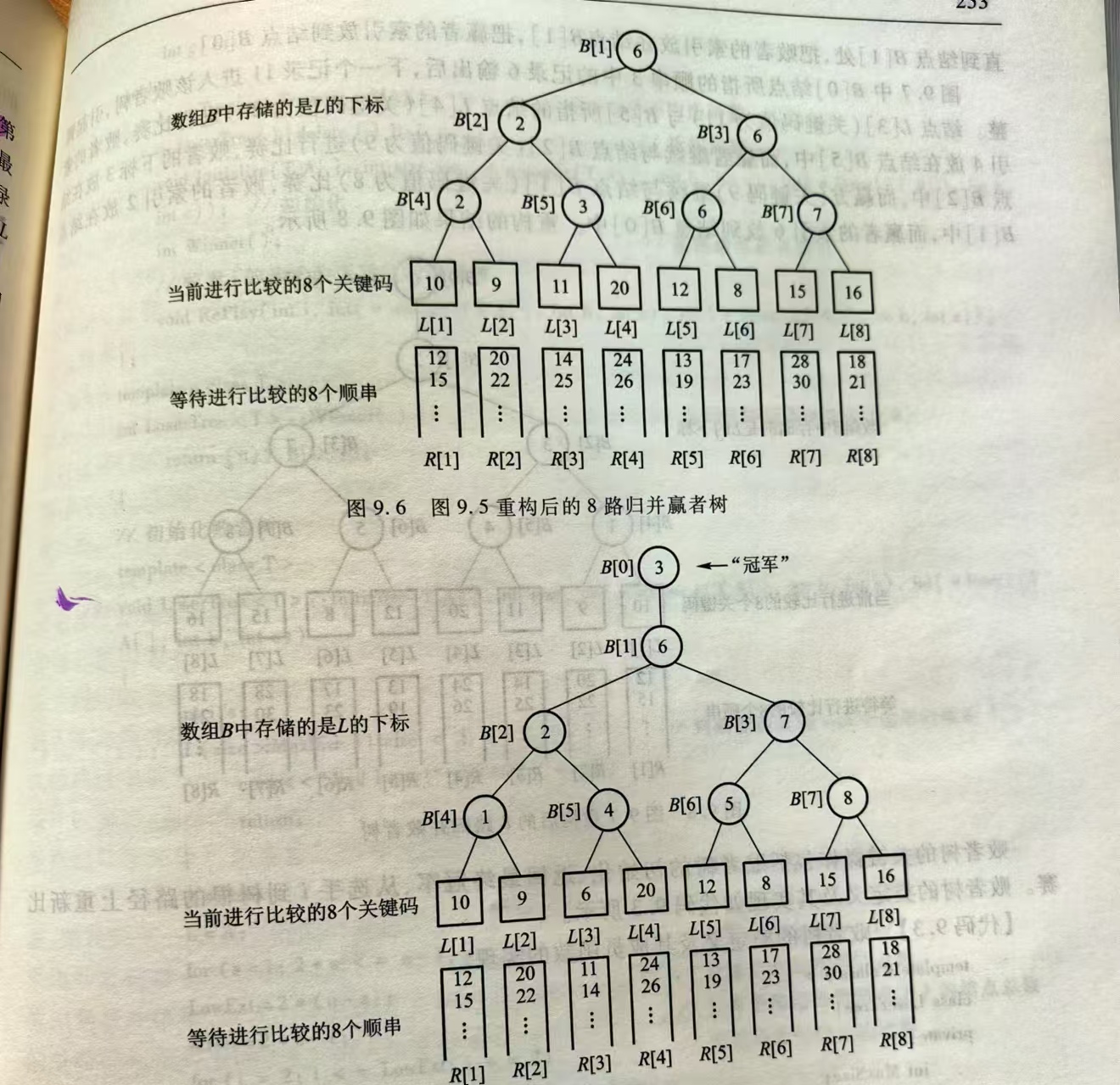
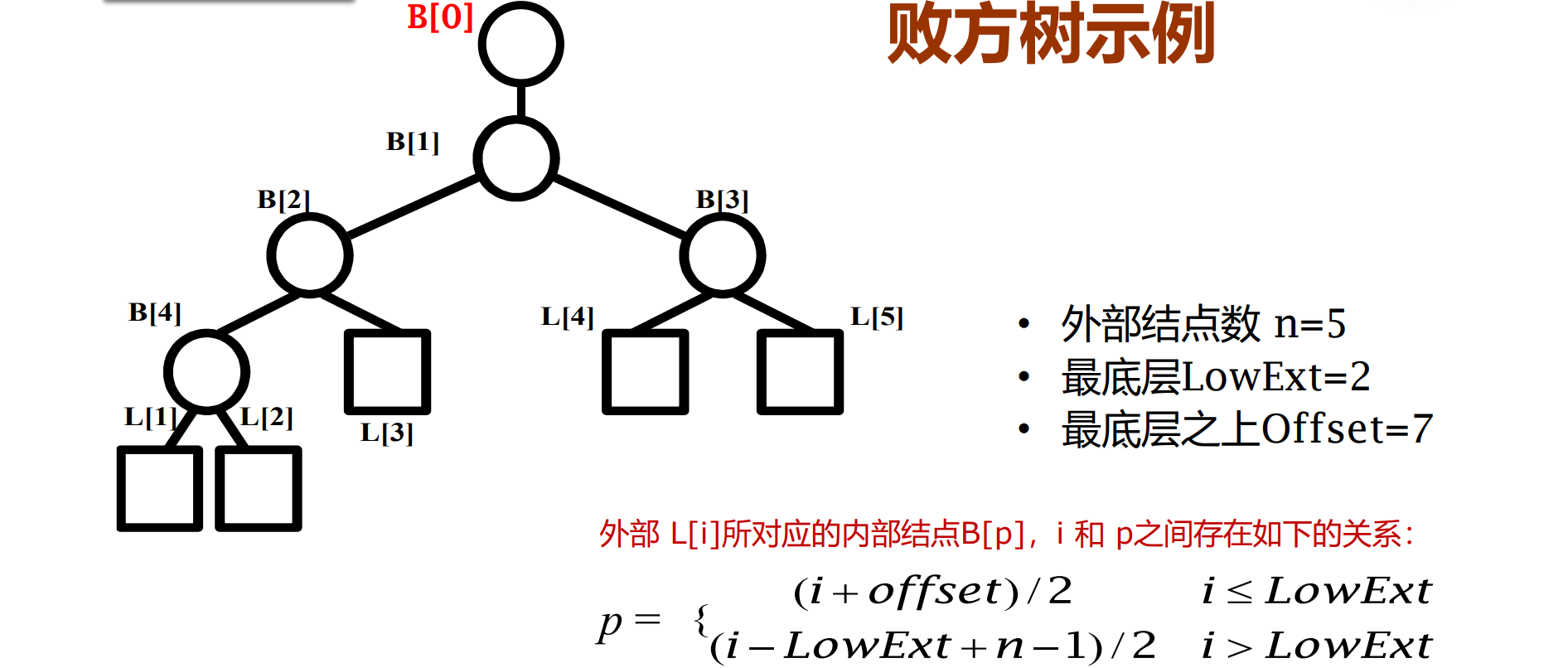
败方树 ADT(胜者树同理)

template<class T>
class LoserTree
{
    private:
        int MaxSize; // 最大选手数
        int n; // 当前选手数
        int LowExt; // 最底层外部结点数
        int offset; // 最底层外部结点之上的结点总数
        int * B; // 败方树数组，实际存放的是下标
        T * L; // 元素数组
        void Play(int p,int lc,int rc,int(*winner)(T A[],int b,int c));
    public:
        LoserTree(int Treesize = MAX);
        ~LoserTree(){delete [] B;}
        void Initialize(T A[], int size,int (*winner)(T A[], int b, int c), 
        int(*loser)(T A[], int b, int c)); // 初始化败方树
        int Winner(); // 返回最终胜者索引
        void RePlay(int i, int(*winner)(T A[], int b, int c), int (*loser)(T A[], int b, int c)); // 位置 i 的选手改变后重构败方树
};
// 成员函数Winner，返回最终胜者 B[0] 的索引
template<class T>
int LoserTree<T>::Winner()
{
    return (n)?B[0]:0;
}

template<class T> // 初始化败方树
void LoserTree<T>::Initialize(T A[], int size, int(*winner)(T A[], int b, int c), int(*loser)(T A[], int b, int c)) 
{
    if (size > MaxSize || size < 2) 
    {
        cout<<"Bad Input!"<<endl<<endl; return; 
    }
    n = size; L = A; // 初始化成员变量
    int i,s; // 计算s=2^log(n-1)
    for (s = 1; 2*s <= n-1; s+=s);
    LowExt = 2*(n-s); offset = 2*s-1;
    for (i = 2; i <= LowExt; i+=2) // 底层外部
        Play((offset+i)/2, i-1, i, winner, loser);
    if (n%2) 
    { // n奇数，内部和外部比赛
        Play(n/2,B[(n-1)/2],LowExt+1,winner,loser); i = LowExt+3;
    } 
    else i = LowExt+2;
    for (; i<=n; i+=2) // 剩余外部结点的比赛
        Play((i-LowExt+n-1)/2, i-1, i, winner, loser);
}

Play 比赛

template<class T>
void LoserTree<T>::Play(int p, int lc, int rc, int(* winner)(T A[], int b, int c), int(* loser)(T A[], int b, int c))
{
    B[p] = loser(L, lc, rc); // 败者索引放在B[p]
    int temp1, temp2;
    temp1 = winner(L, lc, rc);// p处的胜者索引
    while(p>1 && p%2) 
    { // 内部右，要沿路向上比赛
        temp2 = winner(L, temp1, B[p/2]);
        B[p/2] = loser(L, temp1, B[p/2]); 
        temp1 = temp2;
        p/=2;
    } // B[p]是左孩子，或者B[1]
    B[p/2] = temp1;
}

RePlay重构

template<class T> void LoserTree<T>::RePlay(int i, int
(*winner)(T A[], int b, int c), int (*loser)(T A[], int b, int c))
{
    if (i <= 0 || i > n) 
    {
        cout<<"Out of Bounds!"<<endl<<endl; return; 
    }
    if (i <= LowExt) // 确定父结点的位置
        int p = (i+offset)/2;
    else p = (i-LowExt+n-1)/2;
    B[0] = winner(L, i, B[p]); B[p] = loser(L, i, B[p]);
    for(; (p/2)>=1; p/=2) 
    { // 沿路径向上比赛
        int temp = winner(L,B[p/2], B[0]);
        B[p/2] = loser(L,B[p/2], B[0]);
        B[0] = temp;
    } 
}

败者树初始化的思想：
1. 最底层的外部节点从左至右一次两两进行比赛，比赛的结果记录在败者树的内部结点中
2. 其余外部节点比赛时：
  1. 外部结点总数为奇数，倒数第二层最左端的外部节点应该与作为其左兄弟的内部结点比赛，此时剩下尚未比赛的外部结点中第一个处于右子树位置的索引值为lowext+3
  2. 否则，倒数第二层第一个处于右子树位置的外部结点索引为lowext+2
3. 最后完成其余外部节点的比赛
多路归并的效率:
1. 原始方法：找到每一个最小值的时间是Θ(k)，产生一个大小为n的顺串的总时间是 Θ (k*n)
2. 败方树方法:产生一大小为n的顺串的总时间为  (k+nlog k)