可视计算与交互概论 notes整理第5-7章
第五章 反走样
走样与反走样
在屏幕像素密度高的时候,图形整体看起来是连续的;而当屏幕像素比较低,或者对局部进行放大时,我们就能看到大量的影响观感的锯齿
走样(Aliasing)现象:锯齿、混淆、摩尔纹的不自然结果
在本质上,走样现象是我们用离散的像素近似表示连续的图形、图片时离散精度(采样频率)不够导致的。因此不管我们是在光栅化,还是处理图像,还是进行三维渲染,还是进行其他的离散化,当采样频率不够的时候就可能出现走样现象(离散信号会导致中间变化的缺失)
反走样(Anti Aliasing):为了减轻或避免走样现象的技术
信号采样理论
- 固定采样的频率(像素密度),逐渐增加连续信号的频率。连续信号的频率越高,离散化信号偏差越高,走样现象发生越严重
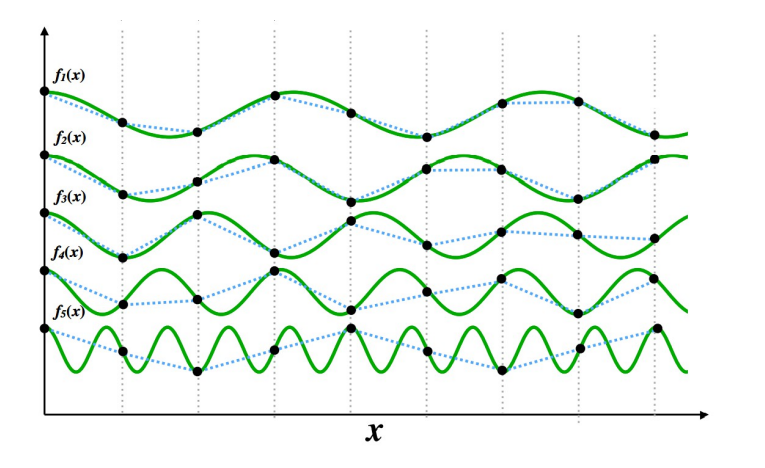
为了从数学上定义到底什么是走样,我们需要借助信号处理中的频域(Frequency domain)分析理论.频域分析的基础是傅里叶变换(Fourier transform):是任意一个信号 f(x) 都可以展开成一系列不同频率的余弦函数 cos(2ωπx) 和正弦函数 sin(2ωπx) 的加和.不同频率对应的强度系数由 F(ω)给出
可以从时域信号 f(x)得到对应的频谱函数 F(ω),也可以从频谱函数 F(ω) 得到时域信号 f(x)。通过傅里叶变换我们可以将所有发生在时域空间里的对信号的操作与对频谱函数的操作一一对应起来
几个重要的观察和结论
- 的非周期信号 f(x)对应频谱函数 F(ω) 在整个频率空间上都有非零值
- 越高频的部分贡献越小,也就是 F(ω) 在 |ω| 很大的时候接近于 0。截断频率ω0表示了整个信号的光滑程度,可以想象当整个信号都很光滑时,ω0 比较小,信号波动比较大或有尖锐的突起时 ω0 比较大
- 在时域空间对信号进行离散采样,对应在频域对信号进行重复更严格的数学叫法是周期延拓(Periodic Extension)对一个截断频率为 f0 的信号以 fs 的频率采样,那么采样得到的离散信号对应的频谱函数,是将原信号的频谱函数在每隔 fs 的位置进行重复
走样现象本质上就是频谱交叠区域引入的不属于原信号的频率特征导致的
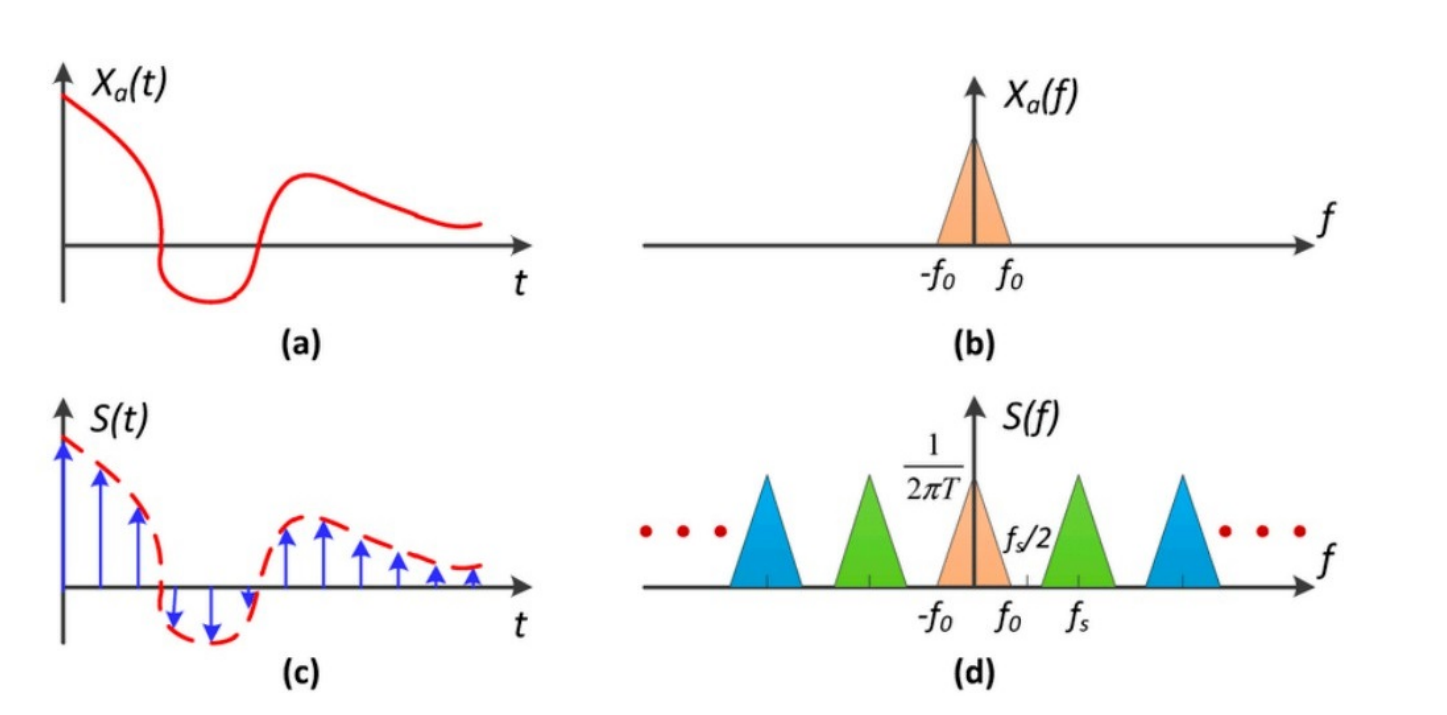
- 如果 fs > 2f0,那么原信号的频谱在采样之后没有发生任何混叠。直接将高频部分的频谱函数进行截断,只保留最中心的原信号的频谱,这样就能无损失地恢复出原信号
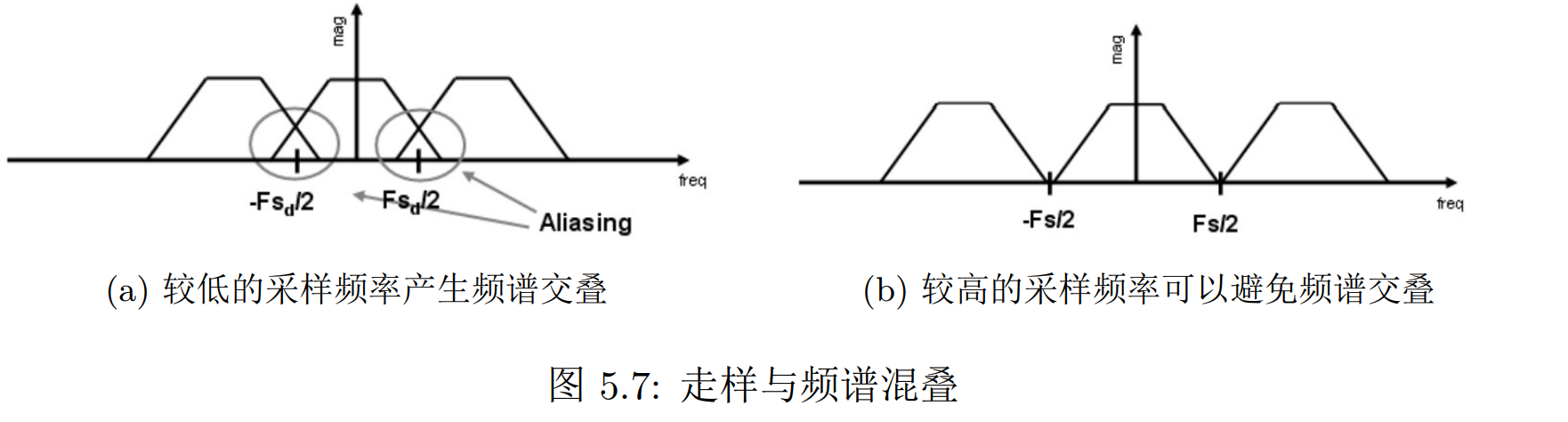
如果 fs < 2f0,那么重复的原频谱之间就会发生交叠,这时频谱函数就会发生混淆,走样现象发生
奈奎斯特-香农采样定理(Nyquist-Shannon sampling theorm):采样频率 fs 至少是原信号截至频率 f0 的两倍即可避免走样现象的发生
反走样的基本原理
- 反走样的目标:尽可能满足奈奎斯特-香农采样定理的条件
- 增加采样频率 fs
- 降低原信号的截止频率 f0
增加fs
增加采样频率的方法就是通过增加每个像素的采样密度
超采样反走样(Super Sample Anti Aliasing, SSAA):可以在每个像素内对称选择多个采样点,比如将像素一分为四,计算每个采样点的颜色然后取平均作为像素的颜色
降低f0(模糊化)
降低原信号的截止频率 f0,也就是对原信号进行模糊化
可以直接截断高频信号。这样采样之后信号就不会发生混叠,也就不会出现类似摩尔纹的走样现象
也可以采用低通滤波反走样
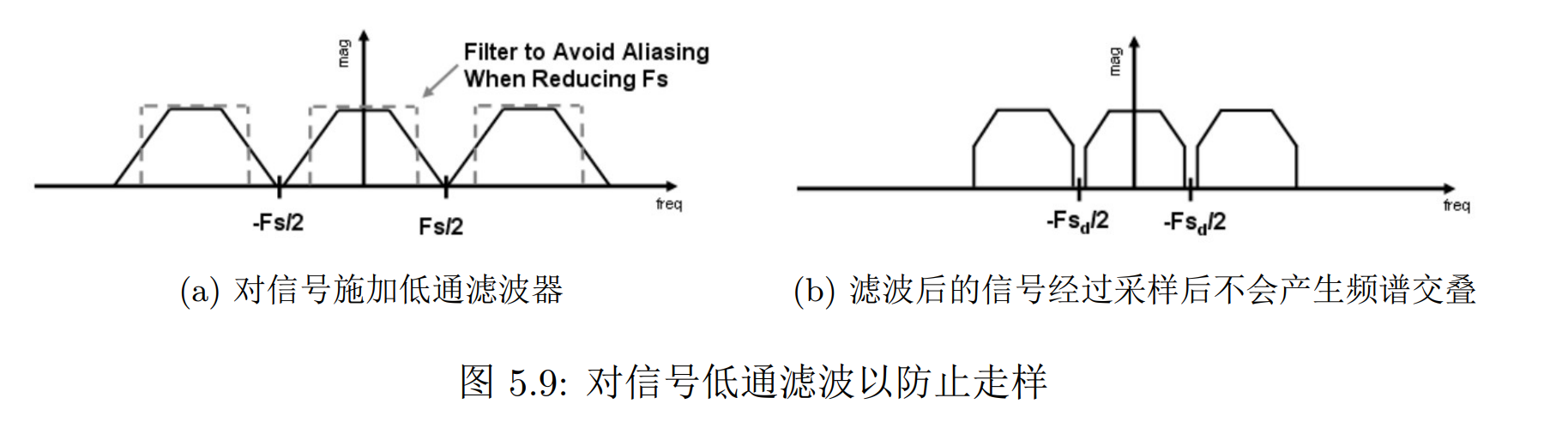
意模糊化一定要发生在光栅化之前。如果光栅化的走样结果已经产生了,再进行模糊化没有办法去掉这些走样,而且会让画面看起来更糟糕
在具体实践中有非常多的反走样算法:多重采样抗锯齿(Multisample Anti Aliasing, MSAA),时间抗锯齿(Temporal Anti Aliasing, TAA)等
第六章 曲线
理论上说,我们可以用多段直线来近似曲线,但这种近似将会消耗较多的计算和存储资源才能达到相对光滑的视觉效果,并且在进行局部放大时仍然显示出走样
可以把曲线或者曲面的表示方式可以分为显式表示和隐式表示两种
- 显式表示:通过给出曲线/曲面上的一系列点的坐标的值或函数表达式来表征曲线,较为直接和简单。例如:点集,函数方程,参数化(参数曲线)参数曲线的优点在于可以容易地得到曲线上点的坐标,也容易可视化。可以得到曲线的梯度/切向方向
- 隐式表示:一般给出曲线/曲面上的点所满足的性质,隐式函数方程是其中最常用的一类。优点是容易对曲线的内部/外部或左侧/右侧进行区分:若存在点 (x0, y0),只需将其代入表达式 f(x0, y0) 并考察其正负即可.而缺点在于难以采样,若要从曲线上得到某点的具体坐标需要通过解方程
从一阶曲线到高阶曲线
直线/线段是一类拥有最简单的数学形式的特殊曲线——一阶曲线,它可以通过在给定的两点间进行线性插值得到,在数学上对应着关于参数坐标 t ∈ [0, 1] 的一阶函数
给定两点 P0, P1 后通过插值获得一阶曲线:这条曲线上的任意一点
的坐标可以看成是参数 t 的函数:P(t) = (1 − t)P0 + tP1, t ∈ [0, 1]插值采用的一阶权重函数 w0(t)=1 − t, w1(t) = t 是关于 t 的线性函数,因此这个操作也被称为线性插值,记为 lerp(P0,P1, t) = P(t)
一阶曲线的优势在于数学形式简单,但它的缺陷是不够视觉上不够“光滑”
G1 光滑:在曲线上任意一点,其两侧曲线的一阶梯度共线且同向
C2 光滑:在曲线上任意一点,其两侧曲线的一阶梯度相等
由线段连接而成的曲线是分段光滑的,但在连接点处,由于两侧线段不共线,因此它的左侧梯度和右侧梯度不共线,无法满足 G1 光滑的条件。这是一阶插值的固有问题
为此我们需要求助于高阶的曲线表示方法。一个最简单的高阶插值方法是拉格朗日插值 (Lagrange interpolation),它利用高阶多项式对给定的点列进行平滑的连接。但拉格朗日插值有两个缺陷:
- 随着点列数量的增加,拉格朗日插值的多项式阶数随之线性增长
- 龙格现象(Runge’s phenomenon):拉格朗日插值拟合出的曲线在边界附近波动较大,微小噪声就有可能造成曲线图像的大幅度改变,曲线两端出现剧烈的抖动
贝塞尔曲线
- 贝塞尔曲线 (Bézier curve)通过在端点之间额外引入一系列点来达成对曲线形状的控制,这些点 (包括端点) 被统称为控制点。通过对控制点进行调整,我们可以轻松地控制贝塞尔曲线的形状和高阶特征
数学形式
一条二阶贝塞尔曲线是通过两轮线性插值通过德卡斯特里奥算法 (de Casteljau’s algorithm)得到:
- 第一轮,由参数 t 对 P0P1 和 P1P2 分别做线性插值,得到由同一个参数 t 分别在上述两条一阶曲线上对应的点
Q0 = lerp(P0,P1, t) = (1 - t)P0 + tP1
Q1 = lerp(P1,P2, t) = (1 - t)P1 + tP2 - 第二轮,通过对 Q0Q1 做线性插值得到,得到同一个参数 t 对应的点
S = lerp(Q0, Q1, t) = (1 - t)Q0 + tQ1 - 令 t 遍历 [0, 1] 取值范围,即得到由 P0,P1,P2 控制的二阶贝塞尔曲线
- 第一轮,由参数 t 对 P0P1 和 P1P2 分别做线性插值,得到由同一个参数 t 分别在上述两条一阶曲线上对应的点
进而我们可以将贝塞尔曲线的阶数推广到任意高,n 阶贝塞尔曲线由 n + 1 个控制点给出
但贝塞尔曲线每个控制点对曲线的影响不是局部的,因此随着阶数的提高,通过控制点对曲线形状做出有效控制的难度也随之提高
n 阶贝塞尔曲线的数学表达式为:
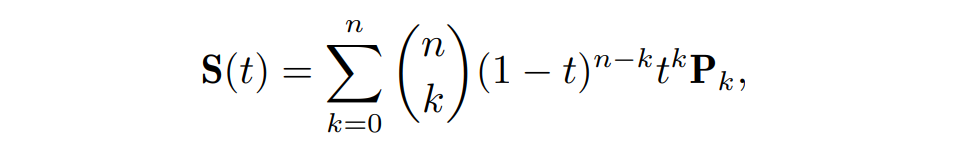
- n 阶伯恩斯坦多项式 (Bernstein polynomials):
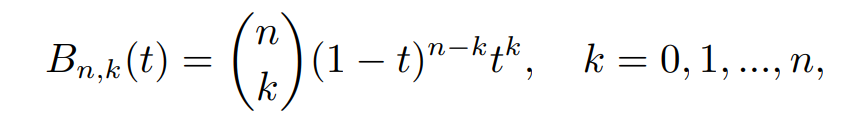
性质
- 贝塞尔曲线的端点:S(0) = P0, S(1) = P1,即,贝塞尔曲线必然经过两端控制点,但一般来说不会经过中间其余控制点
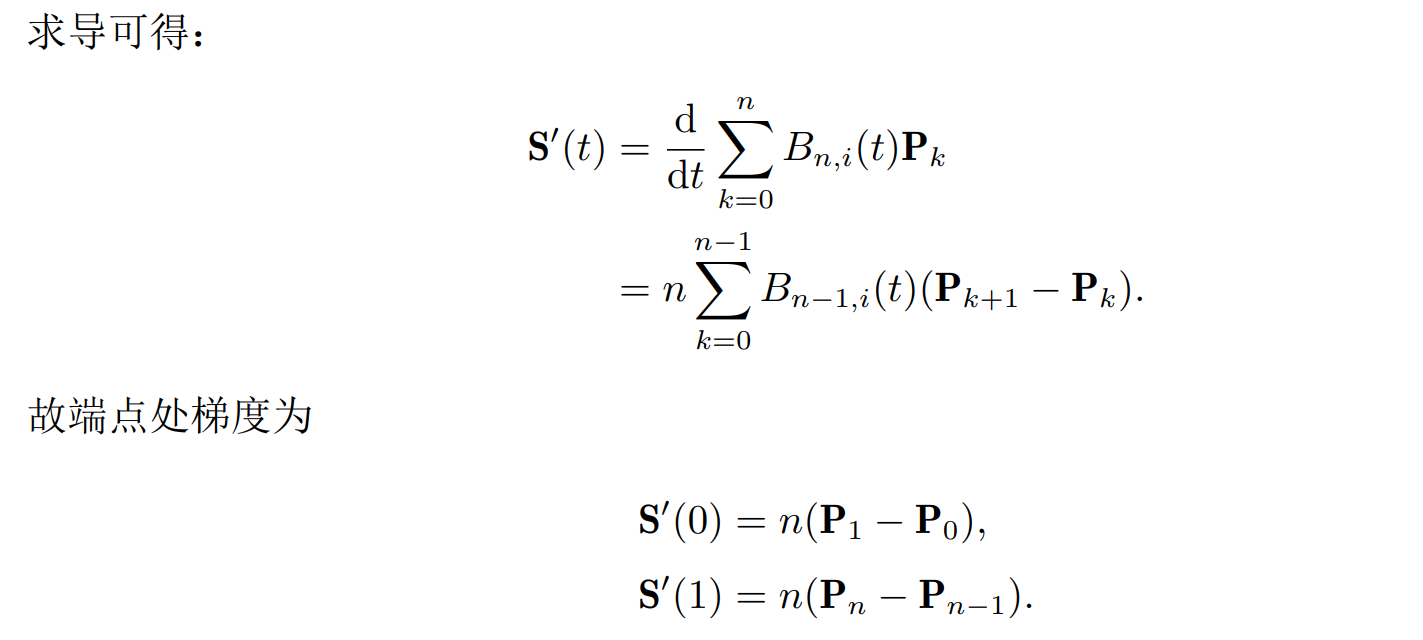
端点处切线分别沿着 P0P1 连线和 PnPn-1 连线的方向
G1 光滑:只需要施加边界条件令它们在公共端点两旁的控制点在同一条直线上即可
C1 光滑:还需要令 ||Pn - Pn-1|| = ||Pn+1 - Pn||,即,约束加强为 Pn − Pn−1 = Pn+1 − Pn
贝塞尔曲线另一条重要的性质是凸包性质 (convex-hull property):贝塞尔曲线被包围在由它所有控制点组成的最小凸包当中
凸包性能帮助我们很好地规划贝塞尔曲线的路径
样条曲线
样条曲线 (spline curve)不依靠另加约束就可以满足整条曲线的 C1 光滑的性质
样条函数作为构成样条曲线的函数基底,具有紧支撑 (compact support) 的特性:每个样条函数只会在一个子区间内取非零值,而在该子区间外取值为 0。因此每个样条函数只会对曲线的某个局部产生影响,这就为对曲线形状进行局部的控制与调整提供了便利
样条函数的分类:
- 曲线近似的样条 (approximation splines):不保证拟合出的曲线过每个控制点,但拥有凸包性质,如 B 样条
- 曲线插值的样条 (interpolation splines):保证拟合出的曲线过每个控制点,但不具有凸包性质,如二次样条、三次样条
B 样条
B 样条是样条函数的一种,它是基函数样条 (basis splines) 的简称
节点 (knots):选定参数区间 [a, b] 内一列非减的数列,满足:a = t0 ≤ t1 ≤ ··· ≤ tm = b,这 m + 1个数将参数区间划分成 m 段
节点向量 (knot vector):由这 m + 1 个节点组成的集合
一个 n 阶 B 样条是由所有次数不超过 n 的 B 样条基 (B-spline basis functions) 组成的
记第 i 个 p 次 B 样条基为 Ni,p(t),它们是一组根据 Cox de Boor recursion 递归定义的函数:
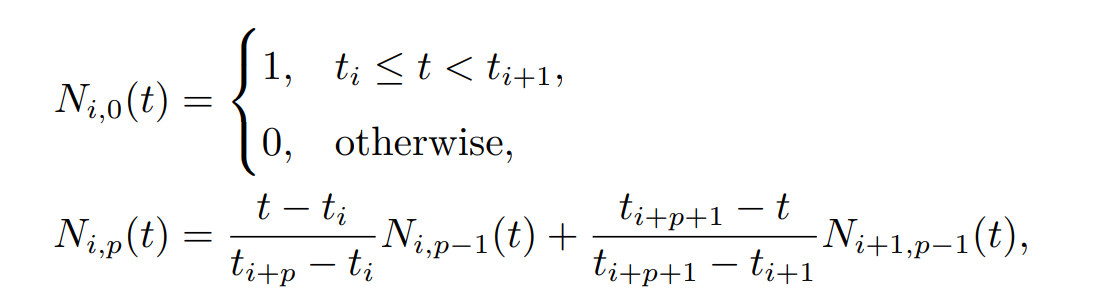
- 并满足性质:
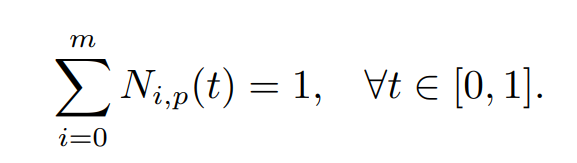
- 给定控制点点列 {P0, P1, …, Pm},那么利用 n 次 B 样条得到的拟合结果即为:
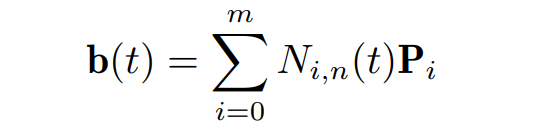
这个过程既可以看成是以 B 样条基为权重函数对点列 {Pi} 进行拟合,也可以看成是以 {Pi} 为权重对 B 样条基进行线性组合,从而将局部曲线组装成全局曲线
当 B 样条的阶数增加时,单个 B 样条基的作用范围也在扩大,每个 p 阶的 B 样条基在 p + 1 个连续子区间上取非零值,也将单个节点的对曲线的影响效果扩展到 p + 1 个附近子区间
节点的数值是可以相同的,若存在 ti = ti+1 = ··· = t + i + k − 1,k> 1,则称其为一个重复度为 k 的多重节点 (multiple knot),否则称其为一个简单节点 (simple knot)
重复会降低该节点处的光滑度要求,p 阶 B 样条曲线在重复度为 k 的节点处是 Cp−k 光滑的
剪裁 B 样条 (clamped B-splines):若令两端的节点重复 p+ 1 次,B 样条曲线将会经过两端端点并且两端切线平行于控制点连线
闭合 B 样条 (closed B-splines):重复首尾的节点和控制点
若一条剪裁 B 样条曲线除两端端点外剩余内部控制点数为 p − 1,那么它就等价于一条p 阶贝塞尔曲线
重要扩展:非均匀有理 B 样条 (non-uniform ration B-splines,简称NURBS)。“非均匀”指的是 B 样条的节点在参数区间内不等距分布,“有理”指的是 B 样条对每个控制点也额外施加了一个权值,当权值均等于 1 时,NURBS 曲线就退化成了普通的 b 样条曲线
因此 NURBS 实质上是齐次坐标 (homogeneous coordinate) 思想下的 B 样条,用权值的形式取代了多次重复设置节点这一笨重的操作,一条 NURBS 曲线的数学形式一般为:
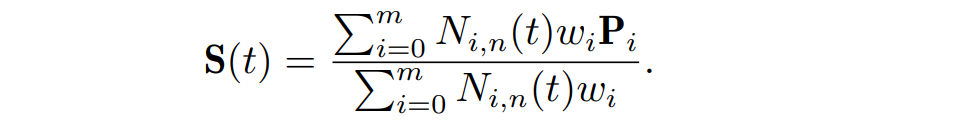
三次样条
而两点不能唯一决定一条曲线段,因此在进行高阶插值时,需要添加额外的约束来帮助我们决定高阶函数系数,如端点处的导数约束或二阶导数约束,从而作出合理的插值
给出点列 {P0, P1, …, Pm},其中每个点的坐标为 Pi = (xi, yi)T, i = 0,…,m.三次样条曲线假设每个子区间 [xi−1, xi], i = 1,…, m 内的曲线段可以用一个三次函数来刻画:fi(x) = aix3 + bix2 + cix + di,并且满足的如下的连续性要求:
- fi(x) 两端满足插值特性
fi(xi−1) = yi−1, fi(xi) = yi, i = 1, ··· , m - 公共顶点的一阶导数连续
fi’ (xi) = fi+1’(xi), i = 1, ··· , m − 1 - 公共顶点的二阶导数连续
fi” (xi) = fi+1”(xi), i = 1, ··· , m − 1
- fi(x) 两端满足插值特性
对 m + 1 个点做三次样条插值,m 段曲线共包含 4m个待定系数,相应地,需要 4m 个约束来帮助我们确定系数.以上三组连续性要求共ᨀ供了 2m + (m − 1) + (m − 1) = 4m − 2 个约束,剩余两个约束来源于对最两侧的线段端点 (x0, y0) 和 (xm, ym) 的约束
边界条件(boundary conditions):额外引入的对最外侧端点的约束:
- 给定端点处的一阶导数 f1’(x0), fm’(xm)
- 给定端点处的二阶导数 f1” (x0), fm”(xm),全为 0 时一般称为自然边界条件
- 周期性边界条件:若点列中 y0 = ym,另外要求 f1’(x0) = fm’(xm), f1” (x0) = fm”(xm),则可得到周期性三次样条
三次样条曲线是使得泛函 J(f) = 从x0到xm积分(|f”(x)|²dx)值最小的函数,而曲线的二阶导是对曲线曲率的近似刻画
三次样条曲线保证了曲线的插值特性,并且满足全局 C2 光滑的特性,即,曲线上一阶、二阶导数处处存在且连续
曲线图形的光栅化
为了将曲线显示在屏幕上,我们同样需要对曲线进行光栅化操作将其转化成位点阵图
自适应细分 (adaptive subdivision)根据曲线不同位置的曲率大小动态地调整细分的程度,从而在弯曲程度较大的地方获得更多的细节而在平滑的地方节省算力
曲线版本的 DDA 算法:根据参数 t 对曲线进行采样,并将采样对应的像素点绘制在屏幕上.为了提高效率,采样可以通过增量累加的方式进行的
用变体的布雷森汉姆算法:曲线的情形下,像素点 (x, y)到曲线的偏差可以定义为 e = F(x, y),这里 F(x, y) 是曲线转化成对应的隐式方程,当像素点在曲线上时,偏差值为 0。对于曲线F(x, y)=0,首先对曲线进行细分从而保证其分段单调。不妨假设其单增,当我们已绘
制像素点 (x, y),算法需要从 (x + 1, y), (x, y + 1), (x + 1, y + 1) 中选取下一个需要绘制的点,算法以 (x + 1, y + 1) 的角度考察是否需要在 x 或 y 方向上步进一个像素:分别计算偏差值 ex = F(x, y + 1), ey = F(x+ 1, y), exy = F(x+ 1, y + 1) 若偏差 | exy | < | ex |,则需要在 x 方向上加 1;若偏差 | exy | < | ey |,则需要在 y 方向上加 1。条件等价于:ey +exy > 0及 exy + ex < 0,由此来确定变体布雷森汉姆算法的下一个绘制点对于由曲线组成的图案类似地可以利用扫描线方法绘制:当扫描线与图形产生多个交点时,第奇数交点到第偶数交点的中间线段对应需要绘制的像素,而第偶数交点到第奇数交点间的线段则不需要绘制
TTF(truetypefont) 文件格式在渲染字体时将采用了类似的思想:将外部轮廓定义为顺时针环绕而内部轮廓定义为逆时针环绕,从某一像素点 P 向任意方向做射线,当自左向右跨越轮廓边界时将环绕数加 1,自右向左跨越时将环绕数减 1,于是当最终结果非零时则表示点 P 在内部,为零则表示在外部
第七章 图像表示与处理
图像是指光的能量在一个二维幕布上的分布,可以表示为 E(x, y, λ,t),其中 (x, y) 为在幕布上的坐标,λ 为波长 (反应光在紫色、蓝色、绿色黄色、红色等频段的能量),t 为时间 (在静态图像中,t 是一个固定值,可以被省去)
图像处理是指通过数学算法对图像进行修改来达到一定的目标效果
图像的存储
矢量图与光栅图
- 在计算机中,主要有两种存储图像的方式
- 矢量图:用一个端点序列来表达图像,它来源于老式基于电子束的显示设备,电子束打在屏幕上会留下一系列线段,通过控制电子束的强度决定留在屏幕上的图案
- 光栅图:将连续的图像离散化成一个二维的网格,每个格点叫做一个像素点,在计算机中用一个二维数组存储每个像素点的颜色亮度、透明度等信息;阴极射线显像设备显示光栅图时会以一个固定的模式扫描屏幕
光栅图的存储
每个像素点的颜色都可以使用一个三维向量 (R, G, B) 表达,三个分量分别表示红色、绿色和蓝色的亮度
如果每个像素点有 24 比特的存储空间,那么我们会采用 3 个 8 比特的整数分别表示该像素点的红色、绿色以及蓝色分量.在这种表达中,每个分量有 0 到 255 共 256 种亮度,总共可以表达 2^24 ≈ 1.6 × 107 种颜色
对于一些很轻量的存储方式,例如每个像素点只有 8 比特的空间,一张图片最多只能有 256 种颜色,我们可以采用查找表 (Look Up Table, LUT) 的方式构建一个颜色映射(colormap)
颜色映射可以应用于灰度图像,或者是提前选好的一些颜色,又或者是对于一张图片自适应地选择一些颜色以节省空间
一些图像文件格式
- 一些常见的图像格式有:
- JPEG: Joint Photographic Experts Group Format
- TIFF: Tagged-Image File Format
- GIF: CompuServe Graphics Interchange Format
- PPM: Portable PixMap Format (ASCII or binary)
- EPS: Encapsulated PostScript Format (ASCII)
更深的帧缓冲区
96 比特像素的存储结构:24 比特存储像素点的颜色;然后使用 8 比特存储像素点的透明度,这部分空间又叫做 alpha 通道 (alpha channel);另外还需要 16 比特来表示这个像素点的“深度”,这部分空间又叫做 Z-缓冲区 (Z-buffer);最后,我们采取了双缓冲技术 (double buffering),导致存储空间翻倍
Alpha 通道:有些图片是由多个图层混合在一起而形成的,需要额外存储每个像素点的透明度(alpha 值)。透明度表示该像素点的权重,α = 0 表示完全透明 (该像素点不会对最终图像产生任何影响),α = 1 表示完全不透明 (该像素点就是最终图像显示出的结果)
设当前图片透明度场为 α,背景图片为 B,那么将当前图片作为前景 F 叠加到背景上就是进行如下操作:C = (1 − α) · B + α · F
Z-缓冲区:绘制的物体会有不同的遮挡关系,可以给每个像素加一个数字表示深度,从而让显示器能够方便地处理遮挡关系以正确显示图像。把深度方向设为 z 轴,所以这部分空间就叫做 Z-缓冲区
双缓冲技术:在显示的过程中,我们需要存储两份帧缓冲区,每个时刻只有其中一份是真正用于显示的,另外一份则用于绘图软件进行修改。这个技术允许在显示的同时进行下一帧的绘图操作,可以有效地避免显示的抖动
图像抖动
量化:指将连续的信号值离散化到有限值域上的过程,在图像处理中就是连续的颜色场用计算机中有限的颜色种类尽可能接近原图地表示出来
抖动 (dithering):在数字信号处理领域的中一项用于降低量化误差的技术。透过在较低比特中加入噪声,借此破坏谐波的排序,使谐波的影响受到压制,并减少量化误差在低频的影响
图像抖动的目的:为了消除颜色带现象,让量化后的图片视觉上更加接近原图
问题设置
一张灰度图,其每个像素的亮度值可视为 [0, 1] 范围内的一个实数,现在要将其显示在一个老式显示设备上,每个像素只能取 0 或 1 的亮度值,如何才能让显示的图像在视觉上尽可能接近原图?
最朴素的解决办法:将亮度小于等于 0.5 的像素显示成黑色,否则显示成白色
有序抖动
假设显示器的分辨率高于图像,原图的每个像素点可以用显示器上相邻的 3 × 3 = 9 个像素点来显示。由此,我们可以定义一个 3 × 3 的抖动矩阵 (dithering matrix) M,每个元素对应于显示器上 3 × 3 区域中的一个像素点,若原图相应像素的亮度值大于 Mij/9 (i, j ∈ {0, 1, 2},下同) 则 3 × 3 区域中第 i 行第 j 列的像素点亮度设为 1,否则为 0
由此可见,M 的每个元素定义了一个亮度的阈值,将 [0, 1] 的亮度值拆分成了 10 个集合:{0},(0, 1/9],(1/9, 2/9], · · · ,(8/9, 1],分别对应于 10 种新的亮度
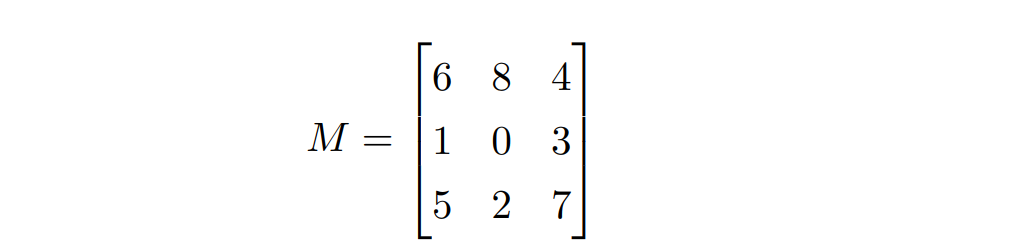
本质:借用了一种超采样的办法减少信息的丢失,如果我们要求显示器分辨率与图像一致,这个方法就不奏效了
有序抖动(ordered dithering) 算法:将原图也划分成紧密排列的 3 × 3 的小区域,每个小区域中第 i 行第 j 列像素的亮度若大于等于 Mij/9 则将其设为 1,否则设为 0
可以将这个算法理解为给整张图片加上了一个以 3 × 3 为周期的噪声,然后再进行二值化处理
基于噪声的抖动
可以将加上的噪声换成另外一些随机生成的噪声,就得到了基于噪声的抖动 (dithering with noise)
噪声的作用:虽然噪声的引入让部分像素点与原始图片的差别更大,但在平均意义下误差变小了,这也是为什么从“整体”上来看,加入噪声反而让量化效果更好
白噪声
白噪声抖动算法 (white noise dithering):对原始图片的每个像素点都加上一个在 [−0.5, 0.5] 中均匀取值的随机干扰,然后再以 0.5 为阈值进行二值化
相比于直接二值化,这个结果能看出灰度的渐变,但总体效果不如有序抖动方法,我们会感觉图片的噪声十分“刺眼”
蓝噪声
蓝噪声抖动算法 (blue noise dithering) :果不仅能看出灰度的渐变,而且相比白噪声抖动而言,我们对图片上噪声的感觉没有那么明显
原因:白噪声的能量在各个频率上接近均匀分布,而蓝噪声的能量则主要集中在高频部分。人类的眼睛对低频信号较为敏感,高频信号则更难被察觉.我们能够明显地察觉到白噪声,但却很难发现蓝噪声的存在
在采样点数目相同的情况下,蓝噪声采样会比白噪声采样看上去更接近原图
基于误差扩散的抖动
弗洛伊德-斯坦伯格抖动算法 (Floyd-Steinberg Dithering):思想是将单个像素的量化误差传递到其他像素,从而保证总误差接近于 0
弗洛伊德-斯坦伯格抖动算法的流程是:从左到右、从上到下依次处理每一个像素点,将当前像素点的亮度以 0.5 为阈值进行二值化,将二值化前的亮度减去二值化后的亮度作为误差值,然后将误差值分成占比分别为 7/16, 3/16, 5/16, 1/16 的四个部分,并分别加到右方、左下方、下方、右下方四个像素的亮度值,已处理好的像素点不受影响
弗洛伊德-斯坦伯格抖动算法的优缺点
- 优点:效果与蓝噪声抖动相当,同时又不会出现有序抖动的规则性斑点
- 缺点:由于它需要不断地扩散误差,所以它的计算速度会更慢
点处理与滤波
- 相当一部分传统的图像处理算法可以被分为两类:
- 点处理:把每个像素独立地进行处理,即每个像素修改后的值是关于它本身的一个函数
- 滤波:综合考虑图像的一个区域 (通常是一个小邻域) 来修改一个像素的值,即每个像素修改后的值是关于它邻域内所有像素值的函数
点处理
形式化地描述点处理算法:(x, y) 处的像素为 a[x, y],输出图片中(x, y) 处的像素为 b[x, y],其中 a[x, y] 和 b[x, y] 可以表示像素的任一种属性 (例如灰度、某个颜色的亮度或透明度),则点处理实现了一个函数 f,将原图的单个像素转换为输出图片的对应像素,即 b[x, y] = f(a[x, y])
不同形式的 f 对应于不同的点处理算法
- f(v) = v.恒等变换,原样输出
- f(v) = 1 − v.反色,即白变黑、黑变白
- f(v) = v^p(p < 1).将图片变亮
- f(v) = v^p(p > 1).将图片变暗
对于彩色图片的处理则是对红、绿、蓝三个通道的亮度分别进行 f(v) 的变换
伽玛校正 (Gamma correction) :上述第3条中 p = 1/2.2 的情形,伽玛校正的主要目的是为了抵消显示器输出对实际亮度的改变,使得校正之后的颜色在视觉上看起来和实际更加相符
滤波
滤波的每个输出依赖于输入中的多个输入,即输出图片的一个像素是输入图片中多个像素的函数,可以写为 b[x, y] = f(a[x1, y1], a[x2, y2], · · ·)
线性移不变滤波 (linear shift-invariant filtering):“线性”是指输出信号的值是输入信号值的线性组合;“移不变”是指对于输出信号的每一位,其输入信号的线性权重都是一致的,不随坐标变化
一维滤波,其形式化的定义如下:其中 x, t 仅取整数值,a[x] 为输入信号,b[x] 为输出信号,h[x] 为滤波器 (filter)
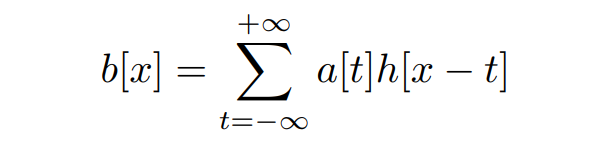
所谓的滤波器就是一组权重,而整个滤波算法就是将输入信号和这一组权重进行卷积:b = a ⊗ h 。卷积满足交换律,即 a ⊗ h = h ⊗ a
二维滤波类似地定义如下:
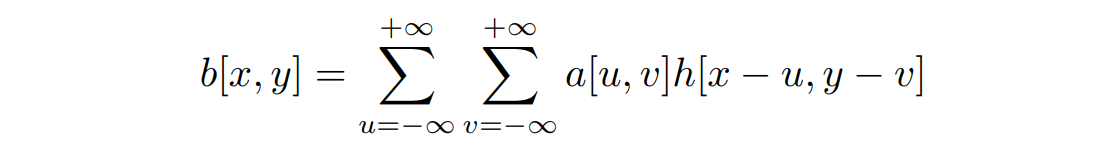
模糊滤镜 (blurring filter)
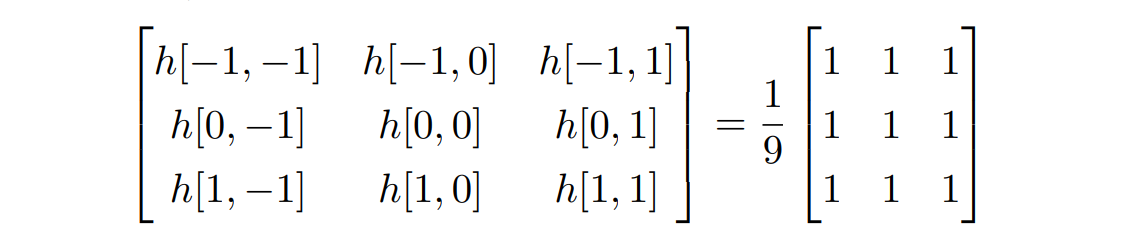
- 更一般地,对于 (2k + 1) × (2k + 1) 的模糊滤波器,h 的取值为
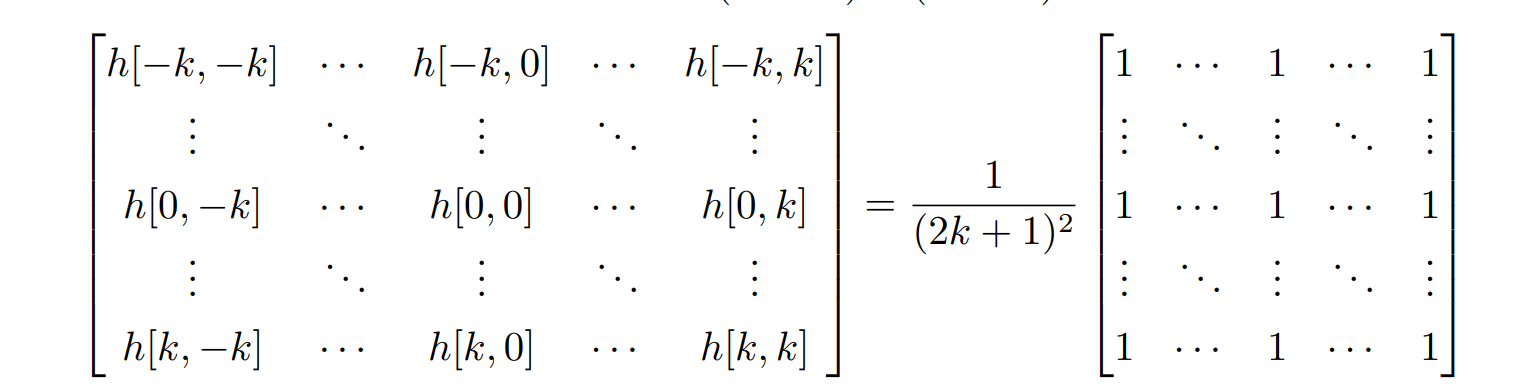
边缘滤波器 (edge filter)
作用:提取出图片中的边缘,输出图片只会保留输入图片中的边界部分。所谓“边界”,就是指图像中一个颜色块过渡到另一个颜色块的交界处,所以边界上的颜色变化比较大,换言之,梯度较大
∂/∂x 和 ∂/∂y 对应于矩阵
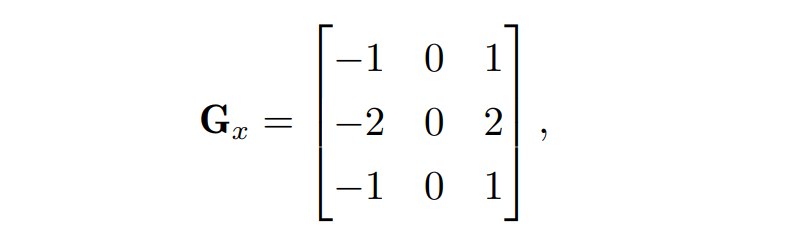
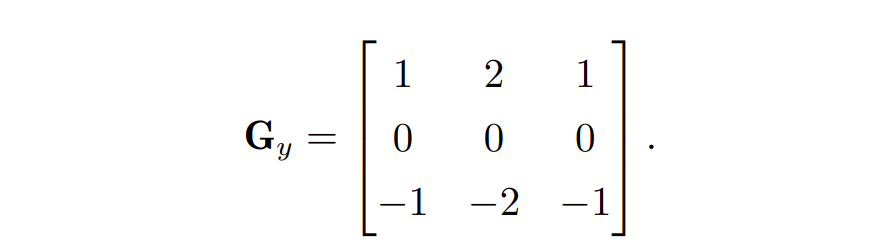
将图片的一个 3 × 3 区域与 Gx 点乘 (即每个位置上的元素对应相乘) 可以得到该区域中心点在 x 方向上导数的近似,与 Gy 点乘则是在 y 方向上导数的近似
将矩阵 Gx 和 Gy 绕中心元素旋转 180◦ 可得相应的滤波器,需要旋转是因为滤波进行的是卷积运算,而矩阵则是用于点乘运算
这两种滤波器要么只对垂直方向的边界敏感,要么只对水平方向的边界敏感,如果想要检测到各个方向的边界,我们需要计算出梯度的模长
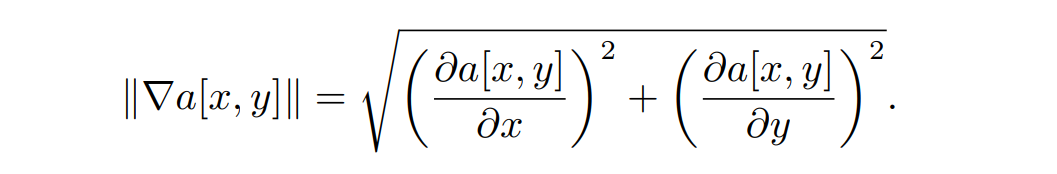
泊松图像编辑
- 泊松图像编辑 (Poisson editing):
- 图像缺失部分的补充(inpainting)使用泊松图像编辑可以很方便地得到一个最自然的填充方式,省去了手动涂色的工作
- 无缝的图像融合 (seamless cloning)使用泊松图像编辑完成这个任务只需要原图中大致圈出树干的区域即可。直接将截取的部分贴到目标图像中,并进行简单的颜色调整
图像补全
在图像补全任务中,我们需要对图像缺失的部分进行填充,并确保填充后的结果尽可能合理。“合理”是指尽可能平滑
- 空间局部性 (spatial locality):图像中同一个物体上相邻的部分应该相似
- 奥卡姆剃须刀原则 (Occam’s razor):被填补的区域不应该存在任何多余的东西,即无法从非填充区域推理得出的东西
数学中,平滑的意思就是让图片亮度的梯度尽可能小,表达为如下最优化问题:找到一个颜色场 f 使得内部的梯度尽可能小,同时边界上能够无缝衔接
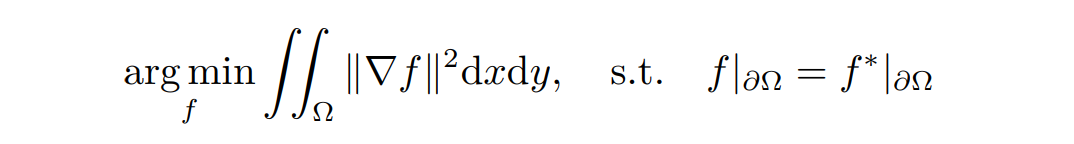
无缝图像融合
- 图像补全的任务只能为图像填上一部分“空白”,如果我们希望填补上用户指定的内容,这个问题就变成了无缝图像融合任务
与图像补全任务不同的是,我们需要在图像融合的过程中保留源图像的纹理信息,也就是要尽可能地保留源图像的梯度,即优化:让填补部分 f 的梯度与 g 的梯度尽可能接近,同时保证边界上无缝衔接
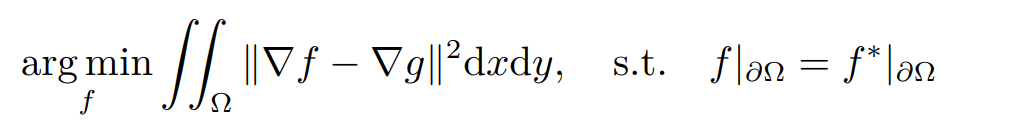
计算问题解决
- 借助欧拉-拉格朗日方程,优化目标取极值当且仅当 f 满足如下狄利克雷边界条件的泊松方程
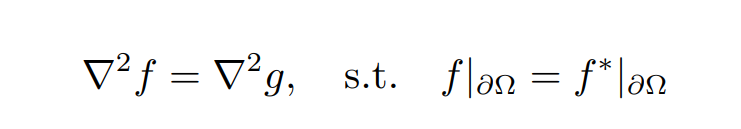
- 为求解 f 我们首先需要估计拉普拉斯算子,这可以通过滤波器来实现
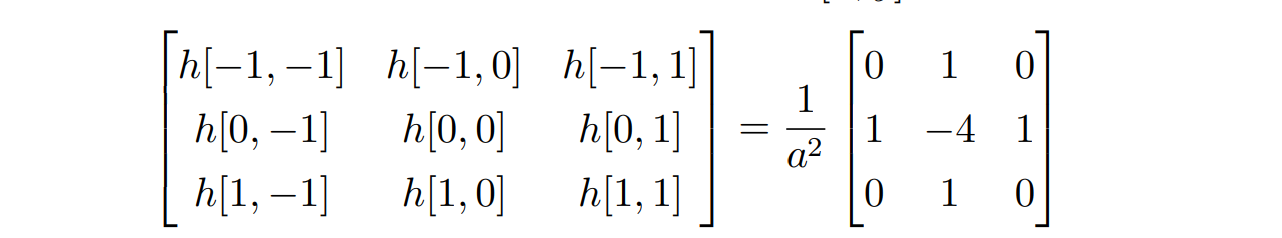
其中 a 表示像素块的边长,其余的 h[x, y] 取 0.至此我们已经可以借助这个滤波器计算出∇²g(x, y), ∀(x, y) ∈ Ω
接下来,将这个滤波器作用在图片上,我们可以写出离散拉普拉斯的表达式:
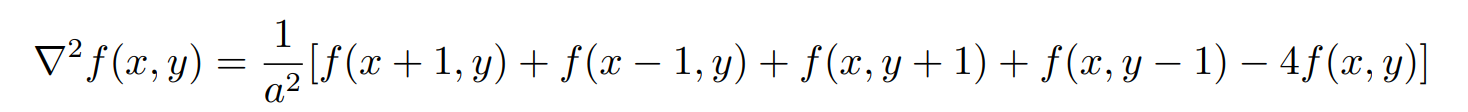
对于大多数 Ω 内的像素点都是成立的,但是对于在边界上的像素点 (和 ∂Ω 相邻的像素点),其四个相邻的像素点不全在 Ω 中,此时我们就需要借助边界条件,把相应的邻居项换成 f∗ 的取值
这样,我们就得到了一个含有 |Ω| 个方程、关于 f(x, y), ∀(x, y) ∈ Ω 的线性方程组.方程与未知数个数相等,求解线性方程组可以得到唯一解
可以进一步将所有的 f(x, y) 排成一个向量 f,并将这个线性方程组写成 Lf = b 的形式。系数矩阵 L 是一个拉普拉斯矩阵,具有性质:
- 稀疏性:由于每个方程只与至多 5 个未知数相关,L 是一个稀疏矩阵
- 对称性:在 Ω 内,如果 (x1, y1) 与 (x2, y2) 相邻,则 ∇²f(x1, y1) 中 f(x2, y2) 一项的系数为 1,且 ∇²f(x2, y2) 中 f(x1, y1) 一项的系数也为 1,否则都为 0,所以这两个系数永远相等
- 主对角占优:L 的对角项为 −4,每一行除对角项外至多还有 4 个 1 (因为至多 4个未知的邻居),非对角项绝对值加起来不超过对角项绝对值
求解方法
- 直接求解法:如 LU 分解
- 迭代法:如雅克比 (Jacobi) 迭代、高斯-赛德尔(Gauss-Seidel) 迭代、逐次超松弛(SOR) 迭代
- 多重网格法
梯度混合
- 为保留墙壁上凹凸不平的纹理,可以令:
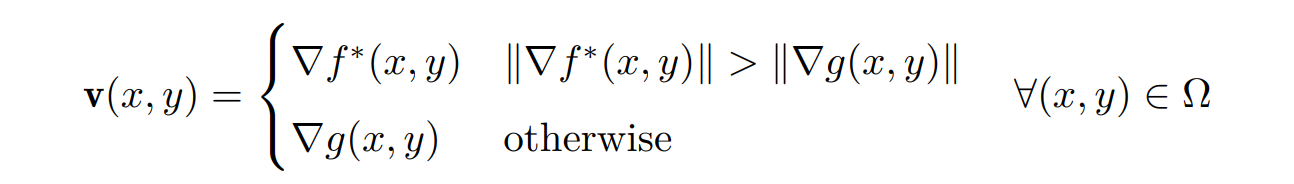
- 其中 f∗(x, y) 指的是背景图的颜色场。要求 f 的梯度尽可能接近源图像和背景图梯度的较大值,这样就可以避免过度平滑的问题了
纹理抹平与去除
- 有时希望将图像的一些纹理抹平,将 v 设为 ∇g,并把其中梯度模长在一个阈值以下的部分修改为 0,即可得到这个效果
图像分割与抠图
- 大多数的图片都会有前景与背景,但是图片本身只有每个像素点的颜色信息。为了从颜色信息还原出前景与背景信息,就需要用到图像分割或者是抠图技术
- 图像分割:对于一些前景背景界限分明的图像,每个像素要么只属于前景,要么只属于背景,从这种图像中恢复前景、背景的任务叫做图像分割 (image segmentation);即,求出一个与原图分辨率一致的二值图片,值为 0 的像素点属于背景,值为1 属于前景
- 前景与背景会有一定程度的混合,此时我们要求的对象就变成了一张透明度图像,每个像素点的值 (0 到 1 的实数) 反映的是前景颜色的占比,这个任务叫做抠图 (image matting)
问题描述
令 C 表示输入的图像,F 表示前景图,B 表示背景图,这些图都是 RGB 图像,α 表示透明度 (或前景图的占比),则它们之间的关系如下式:C = αF + (1 − α)B
对于某一个像素点 i,就是要解如下方程:
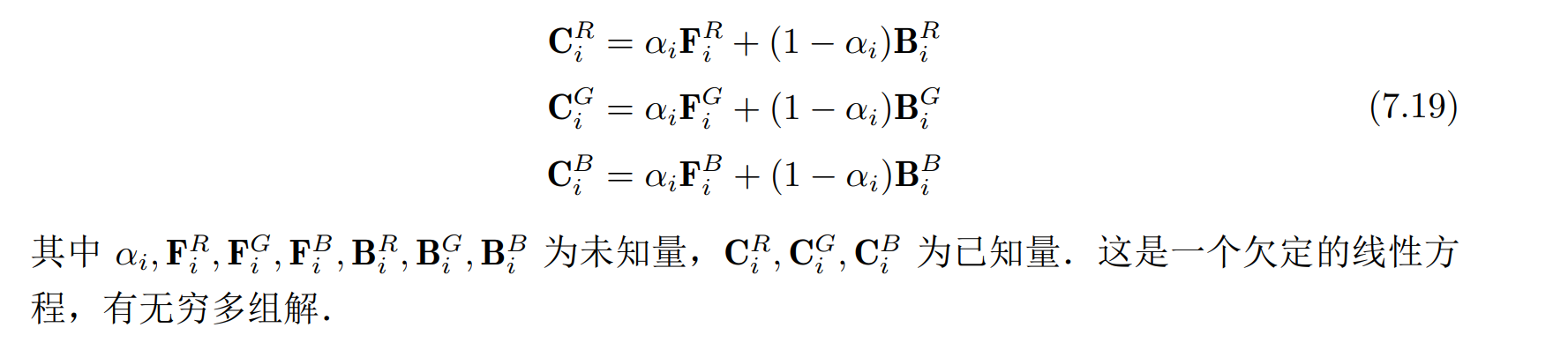
传统的解决方法
- 思路:
- 蓝 (绿) 幕抠图 [blue (green) screen matting]:减少未知量个数
- triangulation matting:增加方程数
蓝 (绿) 幕抠图
- 拍摄时用一片蓝幕作为背景板,那么在处理时就可以假设背景图只有蓝色分量,另外还要假设前景图没有蓝色分量。并且我们还能够知道背景的蓝色分量的值,于是未知量只剩下 3 个:
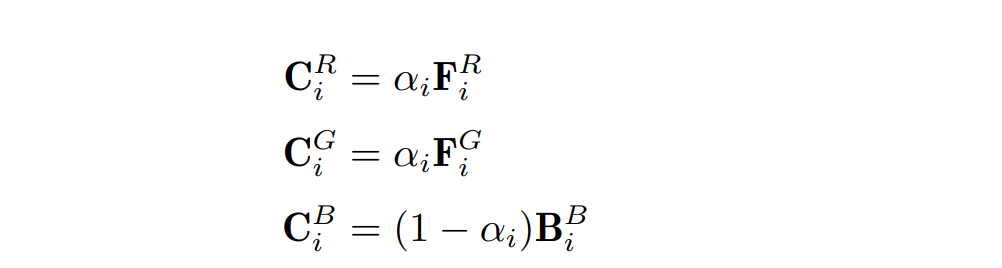
- 缺陷:
- 前景中不可以有蓝色,否则前景的某些区域也会被当成背景从而丢失。这也意味着蓝幕抠图不能应用到透明物体上
- 蓝色背景所反射的光可能会打到前景图上,造成扣取出的前景图边缘偏蓝
Triangulation Matting
- 通过对同样的前景物体配上两组不同的、已知的背景图分别拍摄以弥补这个不足。记另外一张背景图为 Bˆ,其与前景一起拍摄得到的图片为 Cˆ,则方程组变为:

- 优缺点:不再要求前景物体不能包含蓝色分量,不要求背景必须是蓝色,也可以处理透明物体,但是它要求拍摄两张图片的时候前景物体相对相机的位置必须保持一致


