What is torch.nn really? 自学笔记

What is torch.nn really?

• PyTorch通过精心设计的模块和类——torch.nn、torch.optim、Dataset及DataLoader——来协助构建和训练神经网络

• 若要充分发挥其能力并针对具体问题实现定制化，就需要真正理解它们内部的运作机制

• 为建立这种理解，我们将首先在不使用这些模型中任何功能的情况下，在MNIST数据集上训练一个基础神经网络；初始阶段仅使用最基本的PyTorch张量功能

• 随后，逐步每次添加一个来自torch.nn、torch.optim、Dataset或DataLoader的功能组件，清晰展示每个部分的作用，以及它们如何使代码更简洁或更灵活

---

MNIST data setup

• 使用经典的MNIST数据集，它由手绘数字（0到9之间）的黑白图像组成

• 使用pathlib处理路径（属于Python 3标准库），并通过requests库下载数据集

from pathlib import Path
import requests

DATA_PATH = Path("data")
PATH = DATA_PATH / "mnist"

PATH.mkdir(parents=True, exist_ok=True)

URL = "https://github.com/pytorch/tutorials/raw/main/_static/"
FILENAME = "mnist.pkl.gz"

if not (PATH / FILENAME).exists():
        content = requests.get(URL + FILENAME).content
        (PATH / FILENAME).open("wb").write(content)

• 数据集采用numpy array格式，并使用Python特有的数据序列化格式pickle进行存储

• 每张图像的尺寸为28 x 28像素，并以长度为784（28x28）的扁平化行形式存储。需要先将其重塑为二维形式才能查看具体图像

from matplotlib import pyplot
import numpy as np

pyplot.imshow(x_train[0].reshape((28, 28)), cmap="gray")
# ``pyplot.show()`` only if not on Colab
try:
    import google.colab
except ImportError:
    pyplot.show()
print(x_train.shape)

# out:(50000, 784)

• PyTorch使用torch.tensor而非numpy arrays，因此我们需要对数据进行转换

import torch

x_train, y_train, x_valid, y_valid = map(
    torch.tensor, (x_train, y_train, x_valid, y_valid)
)
n, c = x_train.shape
print(x_train, y_train)
print(x_train.shape)
print(y_train.min(), y_train.max())

"""
out:
tensor([[0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.],
        ...,
        [0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.]]) tensor([5, 0, 4,  ..., 8, 4, 8])
torch.Size([50000, 784])
tensor(0) tensor(9)
"""

---

Neural net from scratch (without torch.nn)

• 首先仅使用PyTorch张量操作来创建模型

• PyTorch提供了生成随机或全零张量的方法，我们将利用这些方法为简单线性模型创建权重和偏置

• 这些只是常规张量，但有一个特别重要的附加属性：告知PyTorch这些张量需要计算梯度。这将使PyTorch记录所有在张量上执行的操作，从而能够自动计算反向传播过程中的梯度

• 对于权重参数，我们在初始化后设置requires_grad属性，因为不希望该初始化步骤被包含在梯度计算中（注意：PyTorch中尾部下划线表示原地操作）

• 注：此处我们采用Xavier初始化方法（通过乘以1/sqrt(n)）来初始化权重

import math

weights = torch.randn(784, 10) / math.sqrt(784)
weights.requires_grad_()
bias = torch.zeros(10, requires_grad=True)

• 得益于PyTorch自动计算梯度的能力，我们可以使用任何标准Python函数（或可调用对象）作为模型。只需编写基础的矩阵乘法和广播加法即可创建简单的线性模型

• 同时还需要一个激活函数，这里我们将实现log_softmax并使用它

• 注意：尽管PyTorch提供了大量预写的损失函数、激活函数等组件，但完全可以使用原生Python轻松编写自定义函数。PyTorch甚至会为函数自动生成快速加速器或向量化CPU代码

def log_softmax(x):
    return x - x.exp().sum(-1).log().unsqueeze(-1)

def model(xb):
    return log_softmax(xb @ weights + bias)

• 在上述代码中，@符号表示矩阵乘法运算

• 对单批数据（本例中为64张图像）调用该函数——这便是一次前向传播

• 需要注意的是，由于初始权重为随机值，当前阶段的预测效果不会优于随机猜测

bs = 64  # batch size

xb = x_train[0:bs]  # a mini-batch from x
preds = model(xb)  # predictions
preds[0], preds.shape
print(preds[0], preds.shape)

"""
out:
tensor([-2.6859, -2.6669, -2.2688, -2.6470, -2.6484, -2.0377, -2.0170, -2.3224,
        -1.7795, -2.4400], grad_fn=<SelectBackward0>) torch.Size([64, 10])
"""

• preds 张量不仅包含张量值，还包含一个梯度函数。稍后我们将使用它进行反向传播

• 现在实现负对数似然作为损失函数（可以直接使用标准 Python）

def nll(input, target):
    return -input[range(target.shape[0]), target].mean()

loss_func = nll

• 用随机模型检查损失值，以便观察反向传播后是否有所改善

yb = y_train[0:bs]
print(loss_func(preds, yb))

"""
out:
tensor(2.3058, grad_fn=<NegBackward0>)
"""

• 还需要实现一个函数来计算模型的准确率。对于每个预测，如果最大值对应的索引与目标值相符，则预测正确

def accuracy(out, yb):
    preds = torch.argmax(out, dim=1)
    return (preds == yb).float().mean()

print(accuracy(preds, yb))

"""
out:
tensor(0.1094)
"""

• 运行训练循环。每次迭代中，我们将：

  1. 选择一个minibatch的数据（大小为 bs）
  2. 使用模型进行预测
  3. 计算损失值
  4. loss.backward() 会更新模型的梯度（weights & bias）

• 现在我们使用这些梯度来更新权重和偏置。我们在 torch.no_grad() 上下文管理器中执行此操作，因为我们不希望这些操作被记录到下一次梯度计算中

• 随后将梯度归零，为下一个循环做好准备。否则梯度会持续累加所有已发生的操作记录（即 loss.backward() 会在已有存储值的基础上累加梯度，而不是替换它们）

• 提示：可以使用标准 Python 调试器逐步执行 PyTorch 代码，从而检查每个步骤中的各种变量值

from IPython.core.debugger import set_trace

lr = 0.5  # learning rate
epochs = 2  # how many epochs to train for

for epoch in range(epochs):
    for i in range((n - 1) // bs + 1):
        #         set_trace()
        start_i = i * bs
        end_i = start_i + bs
        xb = x_train[start_i:end_i]
        yb = y_train[start_i:end_i]
        pred = model(xb)
        loss = loss_func(pred, yb)

        loss.backward()
        with torch.no_grad():
            weights -= weights.grad * lr
            bias -= bias.grad * lr
            weights.grad.zero_()
            bias.grad.zero_()

• 至此，我们已经从零开始创建并训练了一个极简神经网络（本例中为 logistic regression，因为没有隐藏层）

• 现在检查 loss 和 accuracy 并与之前的结果进行对比。预期 loss 应该下降而 accuracy 应该上升，实际结果确实如此

print(loss_func(model(xb), yb), accuracy(model(xb), yb))

"""
out:
tensor(0.0835, grad_fn=<NegBackward0>) tensor(1.)
"""

---

Using torch.nn.functional

• 现在将对代码进行重构，使其保持原有功能不变，但开始利用PyTorch的nn类来使代码更简洁灵活

• 第一步通过用torch.nn.functional（通常按惯例导入为F）中的函数替代我们手写的激活函数和损失函数来缩短代码。该模块包含torch.nn库中的所有函数

• 除了各种损失函数和激活函数外，还可以在这里找到一些用于创建神经网络的便捷函数，例如池化函数（此外还有用于卷积、线性层等操作的函数）

• 如果使用的是负对数似然损失和log softmax激活函数，那么PyTorch提供了一个结合了这两者的单一函数F.cross_entropy。这样甚至可以从模型中移除激活函数

import torch.nn.functional as F

loss_func = F.cross_entropy

def model(xb):
    return xb @ weights + bias

print(loss_func(model(xb), yb), accuracy(model(xb), yb))

"""
out:
tensor(0.0838, grad_fn=<NllLossBackward0>) tensor(1.)
"""

---

Refactor using nn.Module

• 接下来使用nn.Module和nn.Parameter来构建更清晰简洁的训练循环。通过子类化nn.Module（它本身是一个能够跟踪状态的类）来实现

• 在这种情况下需要创建一个包含权重、偏置和前向传播方法的类

• nn.Module具有许多我们将用到的属性和方法（例如.parameters()和.zero_grad()）

• 注意：nn.Module（大写M）是PyTorch特有的概念，是一个我们会频繁使用的类。不要将nn.Module与Python中（小写m）module的概念混淆，后者是指可被导入的Python代码文件

from torch import nn

class Mnist_Logistic(nn.Module):
    def __init__(self):
        super().__init__()
        self.weights = nn.Parameter(torch.randn(784, 10) / math.sqrt(784))
        self.bias = nn.Parameter(torch.zeros(10))

    def forward(self, xb):
        return xb @ self.weights + self.bias

• 由于我们现在使用对象而不是单纯使用函数，因此首先需要实例化我们的模型：

model = Mnist_Logistic()

• 现在我们可以用与之前相同的方式计算损失

• 注意：nn.Module对象的使用方式与函数类似（即可调用），但底层PyTorch会自动调用我们的forward方法

print(loss_func(model(xb), yb))

"""
out:
tensor(2.4364, grad_fn=<NllLossBackward0>)
"""

• 在先前的训练循环中，我们必须按名称逐个更新每个参数的值，并手动将每个参数的梯度单独清零

with torch.no_grad():
    weights -= weights.grad * lr
    bias -= bias.grad * lr
    weights.grad.zero_()
    bias.grad.zero_()

• 现在我们可以利用 model.parameters() 和 model.zero_grad()（这两个方法都是由 PyTorch 为 nn.Module 定义的）来简化这些步骤，并降低遗漏某些参数的错误风险，尤其是在模型更为复杂的情况下：

with torch.no_grad():
    for p in model.parameters(): p -= p.grad * lr
    model.zero_grad()

• 将把训练循环封装到fit函数中，以便后续可以重复运行

def fit():
    for epoch in range(epochs):
        for i in range((n - 1) // bs + 1):
            start_i = i * bs
            end_i = start_i + bs
            xb = x_train[start_i:end_i]
            yb = y_train[start_i:end_i]
            pred = model(xb)
            loss = loss_func(pred, yb)

            loss.backward()
            with torch.no_grad():
                for p in model.parameters():
                    p -= p.grad * lr
                model.zero_grad()

fit()

print(loss_func(model(xb), yb))

"""
out:
tensor(0.0815, grad_fn=<NllLossBackward0>)
"""

---

Refactor using nn.Linear

• 继续重构代码，使用Pytorch的nn.Linear类来实现线性层，而不是手动定义和初始化self.weights和self.bias，以及计算xb @ self.weights + self.bias

• Pytorch提供了多种预定义层类型，可以极大简化我们的代码，同时通常还能提升运行效率

class Mnist_Logistic(nn.Module):
    def __init__(self):
        super().__init__()
        self.lin = nn.Linear(784, 10)

    def forward(self, xb):
        return self.lin(xb)

• 按照与之前相同的方式实例化模型并计算损失：

model = Mnist_Logistic()
print(loss_func(model(xb), yb))

"""
out:
tensor(2.3228, grad_fn=<NllLossBackward0>)
"""

fit()

print(loss_func(model(xb), yb))

"""
tensor(0.0814, grad_fn=<NllLossBackward0>)
"""

---

Refactor using torch.optim

• Pytorch 还提供了一个包含各种优化算法的包 torch.optim

• 可以使用优化器中的 step 方法来执行前向步骤，而无需手动更新每个参数。这将使我们能够替换之前手动编写的优化步骤：

"""
with torch.no_grad():
    for p in model.parameters(): p -= p.grad * lr
    model.zero_grad()
"""
opt.step()
opt.zero_grad()

• optim.zero_grad() 会将梯度重置为0，我们需要在计算下一个minibatch的梯度之前调用它

from torch import optim

def get_model():
    model = Mnist_Logistic()
    return model, optim.SGD(model.parameters(), lr=lr)

model, opt = get_model()
print(loss_func(model(xb), yb))

for epoch in range(epochs):
    for i in range((n - 1) // bs + 1):
        start_i = i * bs
        end_i = start_i + bs
        xb = x_train[start_i:end_i]
        yb = y_train[start_i:end_i]
        pred = model(xb)
        loss = loss_func(pred, yb)

        loss.backward()
        opt.step()
        opt.zero_grad()

print(loss_func(model(xb), yb))

"""
out:
tensor(2.3636, grad_fn=<NllLossBackward0>)
tensor(0.0818, grad_fn=<NllLossBackward0>)
"""

---

Refactor using Dataset

• PyTorch 提供了一个抽象 Dataset 类。任何具有 len 函数（通过 Python 标准 len 函数调用）和 getitem 函数（作为索引方式）的对象都可以作为 Dataset

• PyTorch 的 TensorDataset 是一个封装 tensor 的 Dataset

• 通过定义长度和索引方式，它同时提供了沿 tensor 第一维度进行迭代、索引和切片的方法

from torch.utils.data import TensorDataset

• x_train 和 y_train 可以合并到一个 TensorDataset 中，这样更便于进行迭代和切片操作

train_ds = TensorDataset(x_train, y_train)

• 先前需要分别对 x 和 y 的小批量数据进行迭代，现在可以将这两步合并一起实现：

"""
xb = x_train[start_i:end_i]
yb = y_train[start_i:end_i]
"""

xb,yb = train_ds[i*bs : i*bs+bs]

model, opt = get_model()

for epoch in range(epochs):
    for i in range((n - 1) // bs + 1):
        xb, yb = train_ds[i * bs: i * bs + bs]
        pred = model(xb)
        loss = loss_func(pred, yb)

        loss.backward()
        opt.step()
        opt.zero_grad()

print(loss_func(model(xb), yb))

"""
out:
tensor(0.0813, grad_fn=<NllLossBackward0>)
"""

---

Refactor using DataLoader

• PyTorch的DataLoader负责批量数据管理。可以从任何Dataset创建DataLoader

• DataLoader简化了批量迭代过程，无需手动使用train_ds[ibs : ibs+bs]这样的切片操作，DataLoader会自动提供每个minibatch的数据

from torch.utils.data import DataLoader

train_ds = TensorDataset(x_train, y_train)
train_dl = DataLoader(train_ds, batch_size=bs)

• 先前循环是注释这样迭代批次 (xb, yb) 的，现在由于 (xb, yb) 是从数据加载器自动加载的，循环变得简洁得多：

"""
for i in range((n-1)//bs + 1):
    xb,yb = train_ds[i*bs : i*bs+bs]
    pred = model(xb)
"""

for xb,yb in train_dl:
    pred = model(xb)

model, opt = get_model()

for epoch in range(epochs):
    for xb, yb in train_dl:
        pred = model(xb)
        loss = loss_func(pred, yb)

        loss.backward()
        opt.step()
        opt.zero_grad()

print(loss_func(model(xb), yb))

"""
out:
tensor(0.0811, grad_fn=<NllLossBackward0>)
"""

• 得益于 PyTorch 的 nn.Module、nn.Parameter、Dataset 和 DataLoader，训练循环现在显著简化且更易于理解。现在尝试添加在实践中创建有效模型所需的基本功能

---

Add validation

• 第一部分主要致力于为训练数据建立合理的训练循环。实际上始终应该包含验证集（validation set），以便识别是否出现 overfitting

• 对训练数据进行 shuffle 对于防止批次间相关性及 overfitting 至关重要

• 另一方面，无论是否对验证集进行 shuffle，验证损失值都将保持一致。由于 shuffle 需要额外时间，因此对验证数据进行 shuffle 没有意义

• 我们将为验证集使用两倍于训练集的 batch size。这是因为验证集不需要反向传播（backpropagation），因此占用内存更少（不需要存储梯度）

train_ds = TensorDataset(x_train, y_train)
train_dl = DataLoader(train_ds, batch_size=bs, shuffle=True)

valid_ds = TensorDataset(x_valid, y_valid)
valid_dl = DataLoader(valid_ds, batch_size=bs * 2)

• 在每个epoch结束时计算并打印验证损失值

• 注意：在训练前我们总是调用model.train()，在推理前调用model.eval()，这是因为诸如nn.BatchNorm2d和nn.Dropout等层会使用这些状态来确保在不同阶段具有相应的正确行为

• 主要作用：

  1. 启用训练特定行为：
     1. 对 Dropout 层：在训练模式下，Dropout 层会按照设定的概率随机将部分神经元输出置为零，防止过拟合
     2. 对 BatchNorm 层：在训练模式下，BatchNorm 会使用当前批次的统计量（均值和方差）进行标准化，并更新运行平均值
  2. 与评估模式区分：
     1. 对应的 model.eval() 方法会将模型设置为评估模式，关闭上述训练特定行为
     2. Dropout 层在评估模式下会变为直接通过而不丢弃任何神经元
     3. BatchNorm 层在评估模式下会使用训练期间计算的运行平均值和方差，而不是当前批次的统计量

model, opt = get_model()

for epoch in range(epochs):
    model.train()
    for xb, yb in train_dl:
        pred = model(xb)
        loss = loss_func(pred, yb)

        loss.backward()
        opt.step()
        opt.zero_grad()

    model.eval()
    with torch.no_grad():
        valid_loss = sum(loss_func(model(xb), yb) for xb, yb in valid_dl)

    print(epoch, valid_loss / len(valid_dl))

"""
out:
0 tensor(0.2883)
1 tensor(0.3570)
"""

---

Create fit() and get_data()

• 由于在训练集和验证集上计算损失的过程类似，我们将其封装为一个独立的函数 loss_batch，该函数用于计算单个批次的损失

• 对于训练集，我们传入优化器（optimizer）并执行反向传播（backprop）。对于验证集，则不传入优化器，因此该方法不会执行反向传播

def loss_batch(model, loss_func, xb, yb, opt=None):
    loss = loss_func(model(xb), yb)

    if opt is not None:
        loss.backward()
        opt.step()
        opt.zero_grad()

    return loss.item(), len(xb)

• fit 函数运行必要的操作来训练模型，并计算每个周期（epoch）的训练损失和验证损失

import numpy as np

def fit(epochs, model, loss_func, opt, train_dl, valid_dl):
    for epoch in range(epochs):
        model.train()
        for xb, yb in train_dl:
            loss_batch(model, loss_func, xb, yb, opt)

        model.eval()
        with torch.no_grad():
            losses, nums = zip(
                *[loss_batch(model, loss_func, xb, yb) for xb, yb in valid_dl]
            )
        val_loss = np.sum(np.multiply(losses, nums)) / np.sum(nums)

        print(epoch, val_loss)

• get_data 函数返回训练集和验证集的数据加载器（dataloaders）

def get_data(train_ds, valid_ds, bs):
    return (
        DataLoader(train_ds, batch_size=bs, shuffle=True),
        DataLoader(valid_ds, batch_size=bs * 2),
    )

• 现在，我们只需三行代码即可完成获取数据加载器和训练模型的完整流程：

train_dl, valid_dl = get_data(train_ds, valid_ds, bs)
model, opt = get_model()
fit(epochs, model, loss_func, opt, train_dl, valid_dl)

"""
out:
0 0.31063392556905745
1 0.2882448067188263
"""

---

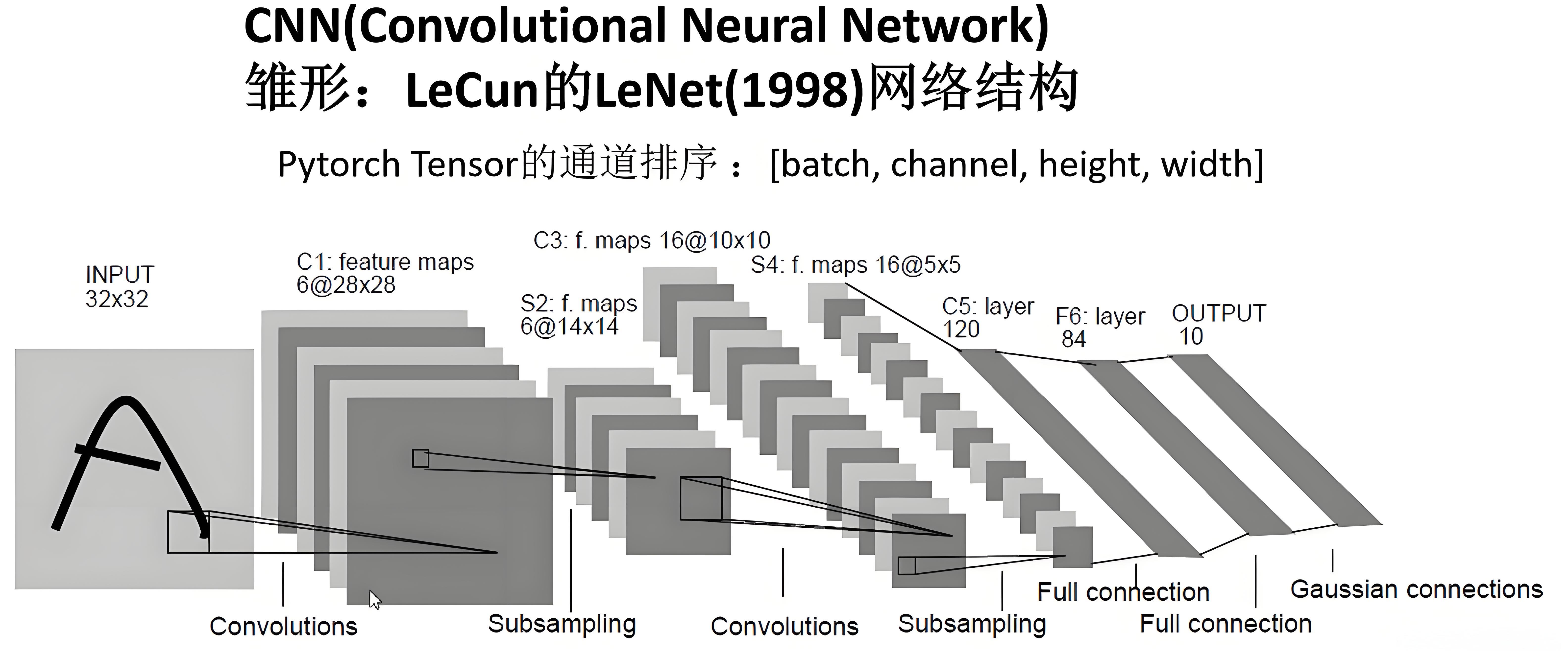
Switch to CNN

• 现在构建一个包含三个卷积层的神经网络。由于之前章节中的所有函数均未对模型形式做任何特定假设，我们将能够直接使用它们来训练CNN而无需任何修改

• 使用PyTorch预定义的Conv2d类作为卷积层。我们定义的CNN包含3个卷积层，每个卷积操作后都接有ReLU激活函数，最后执行average pooling

• 注意：view是PyTorch中与Numpy的reshape功能相对应的方法

class Mnist_CNN(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = nn.Conv2d(1, 16, kernel_size=3, stride=2, padding=1)
        self.conv2 = nn.Conv2d(16, 16, kernel_size=3, stride=2, padding=1)
        self.conv3 = nn.Conv2d(16, 10, kernel_size=3, stride=2, padding=1)

    def forward(self, xb):
        xb = xb.view(-1, 1, 28, 28)
        xb = F.relu(self.conv1(xb))
        xb = F.relu(self.conv2(xb))
        xb = F.relu(self.conv3(xb))
        xb = F.avg_pool2d(xb, 4)
        return xb.view(-1, xb.size(1))

lr = 0.1

• Momentum是随机梯度下降的一种变体，它不仅考虑当前更新，还会纳入之前的更新信息，通常能够加速训练过程

model = Mnist_CNN()
opt = optim.SGD(model.parameters(), lr=lr, momentum=0.9)

fit(epochs, model, loss_func, opt, train_dl, valid_dl)

"""
out:
0 0.2990314514398575
1 0.26232365717291833
"""

---

Using nn.Sequential

• torch.nn 提供了另一个便捷类 Sequential 来简化我们的代码。Sequential 对象会按顺序运行其包含的每个模块

• 为了利用这个特性，需要能够根据给定函数定义自定义层

class Lambda(nn.Module):
    def __init__(self, func):
        super().__init__()
        self.func = func

    def forward(self, x):
        return self.func(x)


def preprocess(x):
    return x.view(-1, 1, 28, 28)

model = nn.Sequential(
    Lambda(preprocess),
    nn.Conv2d(1, 16, kernel_size=3, stride=2, padding=1),
    nn.ReLU(),
    nn.Conv2d(16, 16, kernel_size=3, stride=2, padding=1),
    nn.ReLU(),
    nn.Conv2d(16, 10, kernel_size=3, stride=2, padding=1),
    nn.ReLU(),
    nn.AvgPool2d(4),
    Lambda(lambda x: x.view(x.size(0), -1)),
)

opt = optim.SGD(model.parameters(), lr=lr, momentum=0.9)

fit(epochs, model, loss_func, opt, train_dl, valid_dl)

"""
out:
0 0.42005924537181855
1 0.27518723467588424
"""

---

Wrapping DataLoader

• 当前的CNN相当简洁，但它仅适用于MNIST数据集，原因是：

  1. 假定输入是28*28的长向量
  2. 假定最终的CNN网格尺寸为4*4（因为我们使用了该尺寸的平均池化kernel）

• 让我们消除这两个假设，使模型能够处理任何二维单通道图像。首先，我们可以通过将数据预处理移入生成器（generator）来移除初始的Lambda层

def preprocess(x, y):
    return x.view(-1, 1, 28, 28), y


class WrappedDataLoader:
    def __init__(self, dl, func):
        self.dl = dl
        self.func = func

    def __len__(self):
        return len(self.dl)

    def __iter__(self):
        for b in self.dl:
            yield (self.func(*b))

train_dl, valid_dl = get_data(train_ds, valid_ds, bs)
train_dl = WrappedDataLoader(train_dl, preprocess)
valid_dl = WrappedDataLoader(valid_dl, preprocess)

• 用 nn.AdaptiveAvgPool2d 替换 nn.AvgPool2d，从而允许定义期望的输出tensor尺寸，而不是依赖于输入张量的尺寸。因此，我们的模型将能够处理任意尺寸的输入

model = nn.Sequential(
    nn.Conv2d(1, 16, kernel_size=3, stride=2, padding=1),
    nn.ReLU(),
    nn.Conv2d(16, 16, kernel_size=3, stride=2, padding=1),
    nn.ReLU(),
    nn.Conv2d(16, 10, kernel_size=3, stride=2, padding=1),
    nn.ReLU(),
    nn.AdaptiveAvgPool2d(1),
    Lambda(lambda x: x.view(x.size(0), -1)),
)

opt = optim.SGD(model.parameters(), lr=lr, momentum=0.9)

fit(epochs, model, loss_func, opt, train_dl, valid_dl)

"""
out:
0 0.31809399757385254
1 0.23307032420635224
"""

---

Using your Accelerator

# If the current accelerator is available, we will use it. Otherwise, we use the CPU.
device = torch.accelerator.current_accelerator().type if torch.accelerator.is_available() else "cpu"
print(f"Using {device} device")

"""
out:
Using cuda device
"""

• 更新 preprocess 函数，将数据batches移至accelerator：

def preprocess(x, y):
    return x.view(-1, 1, 28, 28).to(device), y.to(device)


train_dl, valid_dl = get_data(train_ds, valid_ds, bs)
train_dl = WrappedDataLoader(train_dl, preprocess)
valid_dl = WrappedDataLoader(valid_dl, preprocess)

model.to(device)
opt = optim.SGD(model.parameters(), lr=lr, momentum=0.9)

fit(epochs, model, loss_func, opt, train_dl, valid_dl)

"""
out:
0 0.18311398574113846
1 0.17270469266176225
"""

---