自然语言处理 lec4-2 Language Modelling

N-gram Language Models

• 如果我们将每个可能的句子 s 视为空间 S 中的一个点：

• 然而将s的出现次数进行统计，近似，形式化是不可能的

• 解决方法：将问题分解。将每句话看成一个词的序列，视为一个随机变量X1,X2,…,Xn的序列

• 模型预测P(X1 = w1,X2 = w2,X3 = w3,…,Xn = STOP)：

  1. 是一个序列而非集合
  2. 用特殊标记STOP，有时还会有START

• 可以用链式法则进行分解：

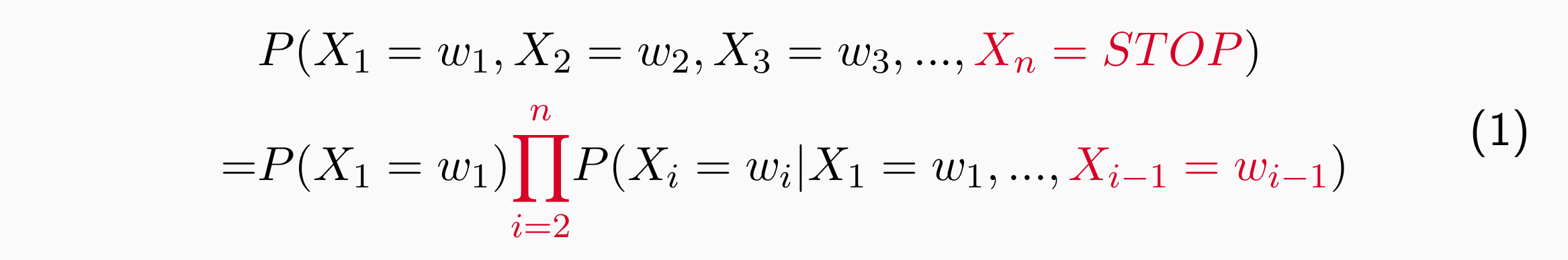
• 问题：很难“看到”历史贡献，当n很大的时候

• 解决方法：需要进行假设

Markov Assumptions

• 当历史很长的时候，是否还需考虑前面的词？当n很大的时候第一个词对最后的词的影响是否很大？

• 大多数时候无需很长的历史，只有前后几个上下文影响下一个词的内容，可以将历史的窗口变小

• First-order Markov assumption:只看前面一个词，一阶假设

• 零阶假设(Unigram Language Model)，完全不考虑历史：效果很差，和朴素贝叶斯模型一样，实质是 bag-of-words (BoW)

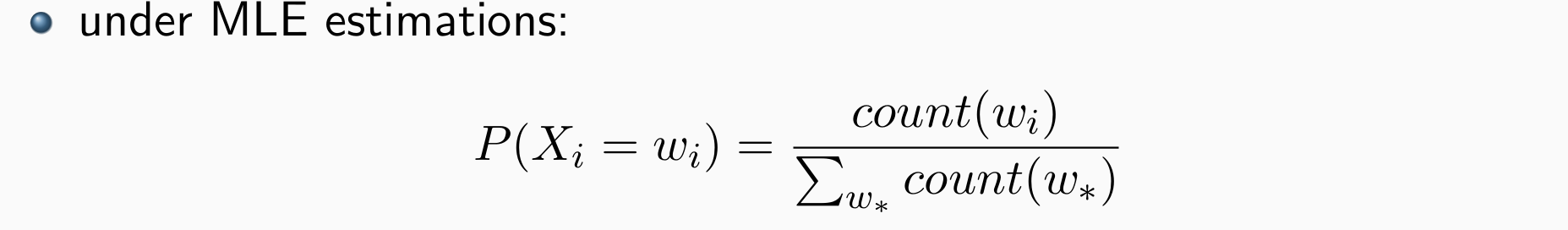
• 完全按照先验的哪些词出现的概率高进行输出(e.g.冠词)

• Second-order Markov assumption(三语言模型):

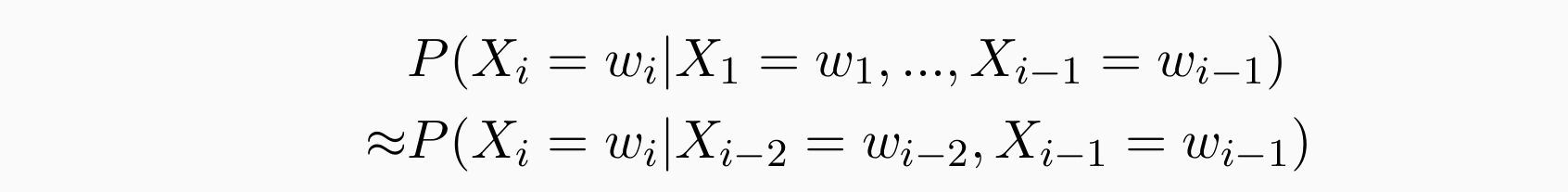
• n阶马尔科夫模型关注n+1个词

N-gram Language Models

• No history assumption → Unigram LM

• First-order Markov assumption → Bigram LM

• Second-order Markov assumption → Trigram LM

• 4-gram LM, 5-gram LM, …再大的话存储代价和近似估计的代价很高，因此一般不超过7-gram LM

• Trigram LM：有限词汇集 V，参数 p(a|b,c), 其中 b, c, a is an arbitrary trigram， a∈V∪{STOP} and b,c ∈V

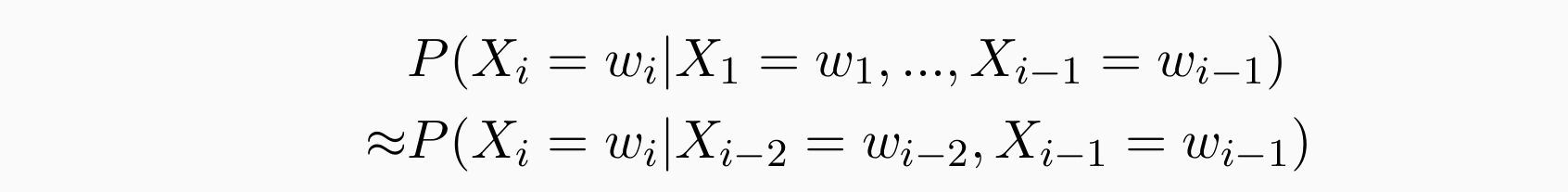
Parameter Estimations

• 问题：句子很长的时候可能得分都非常小，如何估计概率？

• 直观地，给定一个大型语料库：

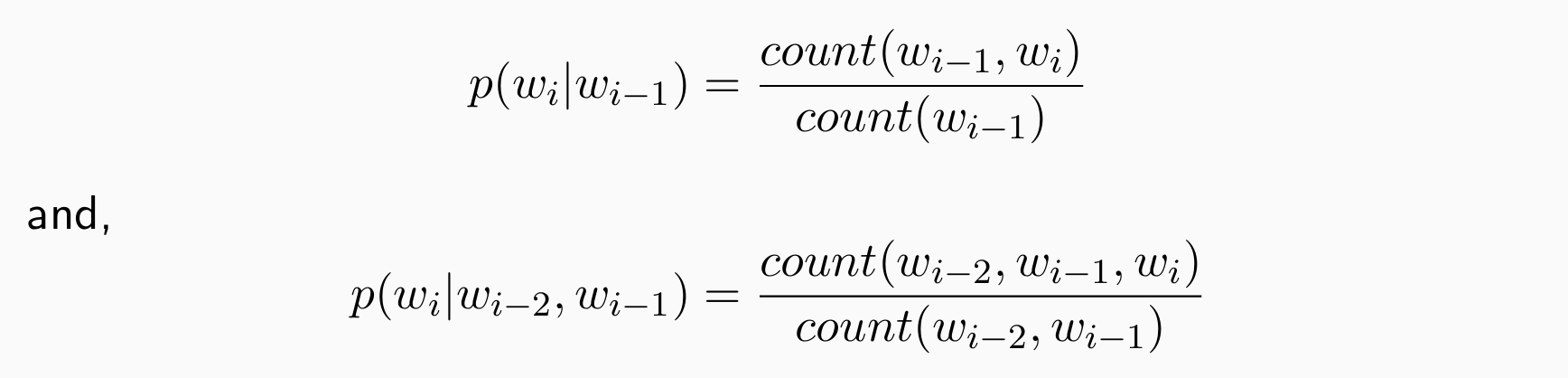
• 用极大似然估计，数据越多，模型效果越好

• the unigram LM needs to store 716,706 probabilities：

  1. bigram LM : 12,537,755
  2. trigram LM : 22,174,483

• 说明在N-gram语言模型中，稀疏性很强，矩阵含有大量的0

Evaluation

How do We Evaluate a Language Model

• 直觉上：一个好的语言模型应该给更“真实”的句子更高的分数

• 最好的语言模型应该最好地预测一个未知的测试集

• 指标：对于一个测试集可以用语言模型：

  1. 计算每句话的概率：p(s)=p(w1,w2,…,wn)，让所有模型都给这句话打分，哪个模型的得分合理就用那个
  2. 计算一整个数据集的所有句子得分相乘，当前模型状态下所有句子同时出现的可能性(数据集的句子都是”好”的句子)：
     
  3. 因为词数不同，因而需要进行归一化：(不是词汇表中的词数)：
     
  4. 取对数进行化简，再去交叉熵：
     
  5. 得到最后的评判标准——歧义度(混淆度)：
     

• 如果每个词的概率都差不多，说明分辨能力差，p(s)小，歧义度得分高，LM效果差

• the lower perplexity, the better LM

Perplexity

• 对于数据集D,词汇表V:如果一个trigram，每个词得分是均匀分布，每个词的得分都一样，p(a|b,c) = 1/(|V|+1)。则perplexity = |V| + 1

• 对于数据集D,词汇表V:如果是一个理想的trigram，说明每句话的概率得分接近1，p(a|b,c) = 1。则perplexity = 1

• perplexity除了可以衡量LM好坏以外还可以衡量某个分支任务的难度，在某个任务的数据集上perplexity高，说明这个任务比较难

Evaluating Language Models

• 使用 Training 数据集估计 n-gram

• test 数据集上的计算perplexity

• 如果要估计不同模型的性能，则必须使用同样的词汇表

• Perplexity 不是下游应用的通用指标

Unigram v.s. Bigram v.s. Trigram … Language Modelling Research

• 直觉上n-gram中n越大LM效果越好

• 但是n越大计算代价高，稀疏性变大

---

Deal with Unseen Events

• 问题：zero-event
  1. 词没见过
  2. 词之间的搭配没见过

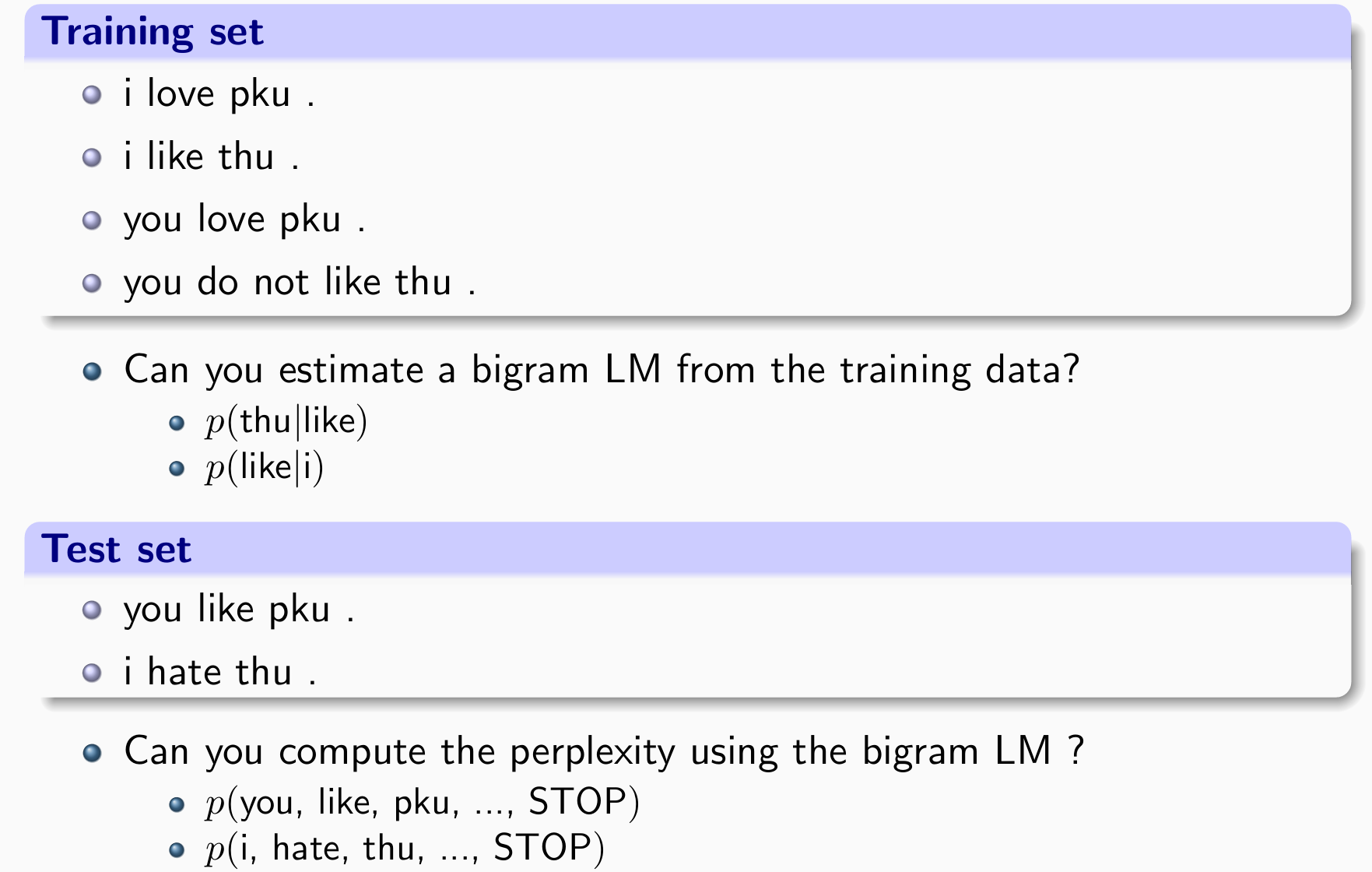
• MLE条件下，zero-event经常出现，MLE 对 Unseen Events 的估计值很差：矩阵中绝大多数元素都是0，有一些是训练集太小没见过，如上例；有一些是句子不合理

• 应该给那些Unseen Events一些概率，这将不可避免地减少 seen 事件的质量：

  1. back-off，从三元文法回退到二元文法
  2. 假设没见过的词都见过一两回，放入新词假设见过
  3. 寻找更好的方法分配一些分数给0

Linear Interpolation

• back-off的实现方法是线性插值

• 使用不同文法进行线性插值，例如trigram使用trigram,bigram和unigram进行线性插值

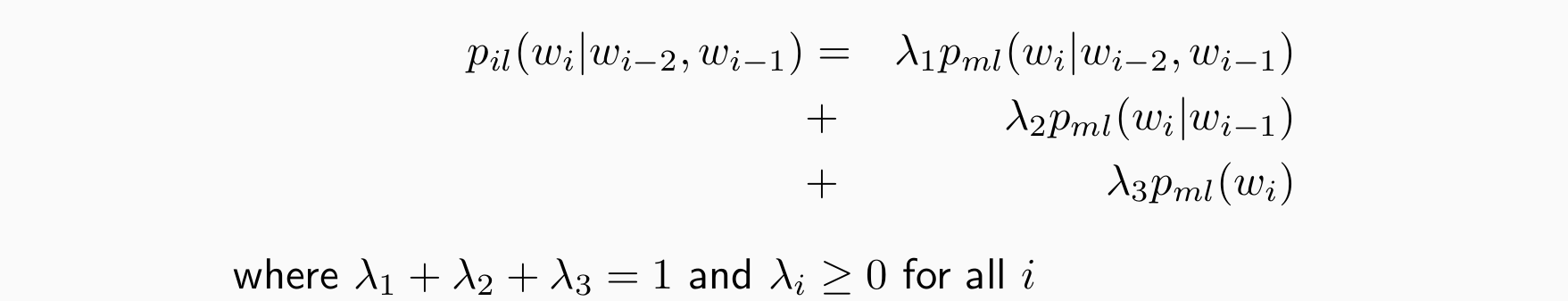
• 问题:如何计算差值权重？

• 将部分训练数据作为验证集，选择 λs 以最大化验证集的对数似然，在 Trigram 情况下：

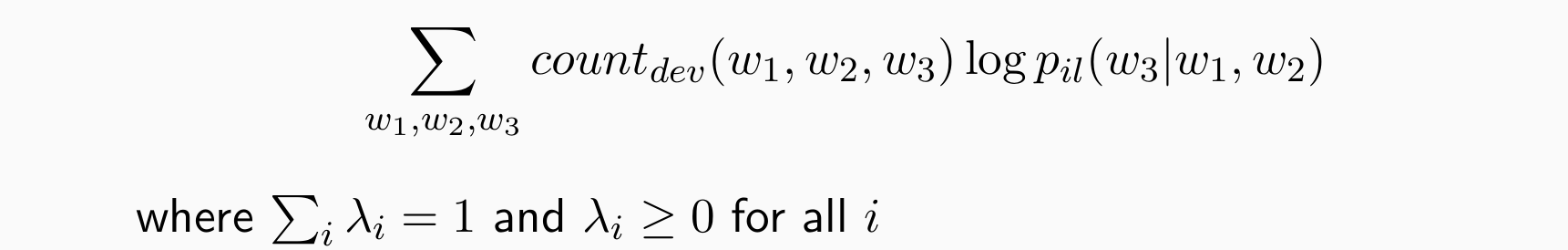
• 实现过程：
  1. Step 1: Initialization: randomly pick values for λ1, λ2, and λ3
  2. Step 2: Calculating
     
  3. Step 3: Re-calculate: λi = ci / (c1 + c2 + c3)
  4. Step 4: if ∆λi > θ, go to Step 2

Stupid Back-off

• 对于 Web 规模的固定词汇表，有 Trigrams ：

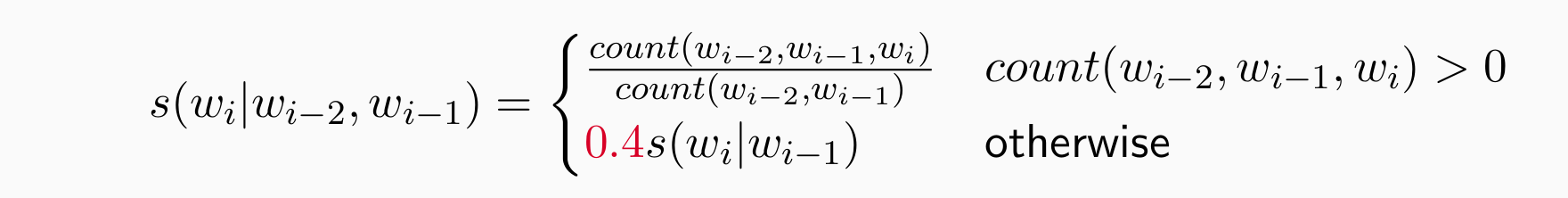
• 不是概率而是一个分数

• 基本假设：频率估计非常可靠，是在大的语料库上得到的，必须是见过的

Smoothing

A Basic Smoothing Solution

• 给矩阵的所有位置+1，从而降低稀疏性，减少矩阵中0的数量

• Add-One Smoothing(Laplace-smoothing)：

• 好处：矩阵中没有0

• 坏处：两个词不应该出现在一起时，都+1会变得不好，对小的训练集影响很大

• 适合场景：希望1的作用能够被“稀释”，因而大的训练集适合用这个方法，而小的训练集会出现大量的0，将大量的0变为1后会导致效果不好

• p(SEEN EVENTS|the) from 1 to 0.36

• p(UNSEEN EVENTS|the) from 0 to 0.64

Good-Turing Discounting

• 动机：假设出现过一两次的事件和没见过的事件差别非常轻微，认为所有没见过的时间概率密度的和等于见过一次的

• 出现r次的单词个数为Nr。将实数 r 转换为调整后的计数 r∗：

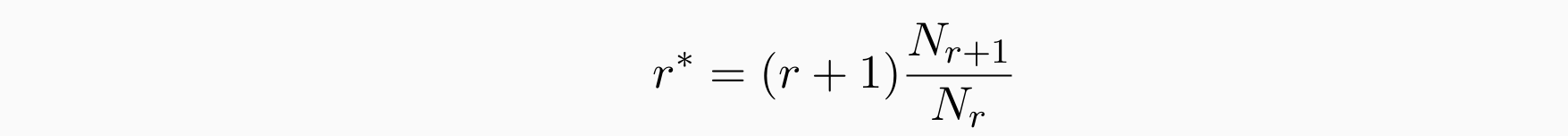
• 为unseen event保留的概率为：N1/Nall

• 对于较大的 r（其中 Nr−1 通常为 0），可以应用各种其他方法（曲线拟合或线性回归）

• 调整后的出现次数都会减少一些，相当于出现多的次，“匀”出来一些给0

• 对于Good-Turing Discounting，有点类似于 r∗ = r − 0.75

• 因此可以从每个计数中减去一个固定数字 d：

Kneser-Ney Smoothing

• Combines various smoothing method：
  1. absolute discounting
  2. considers diversity of history, predicted words
  3. interpolation

---

Beyond N-gram Language Models

More in LM

• Pros：容易构建、可以应用到下游任务…

• Cons：只能考虑很小的context，稀疏性严重，同义词近义词无法表达理解

---