数据结构与算法A 上机考试重点复习
二叉树的struct
二叉树的题必须要完成的第一步:设置一个struct,表示二叉树结点
1234567struct node{ int value; node *left; node *right; node(int v) : value(v), left(NULL), right(NULL) {}};
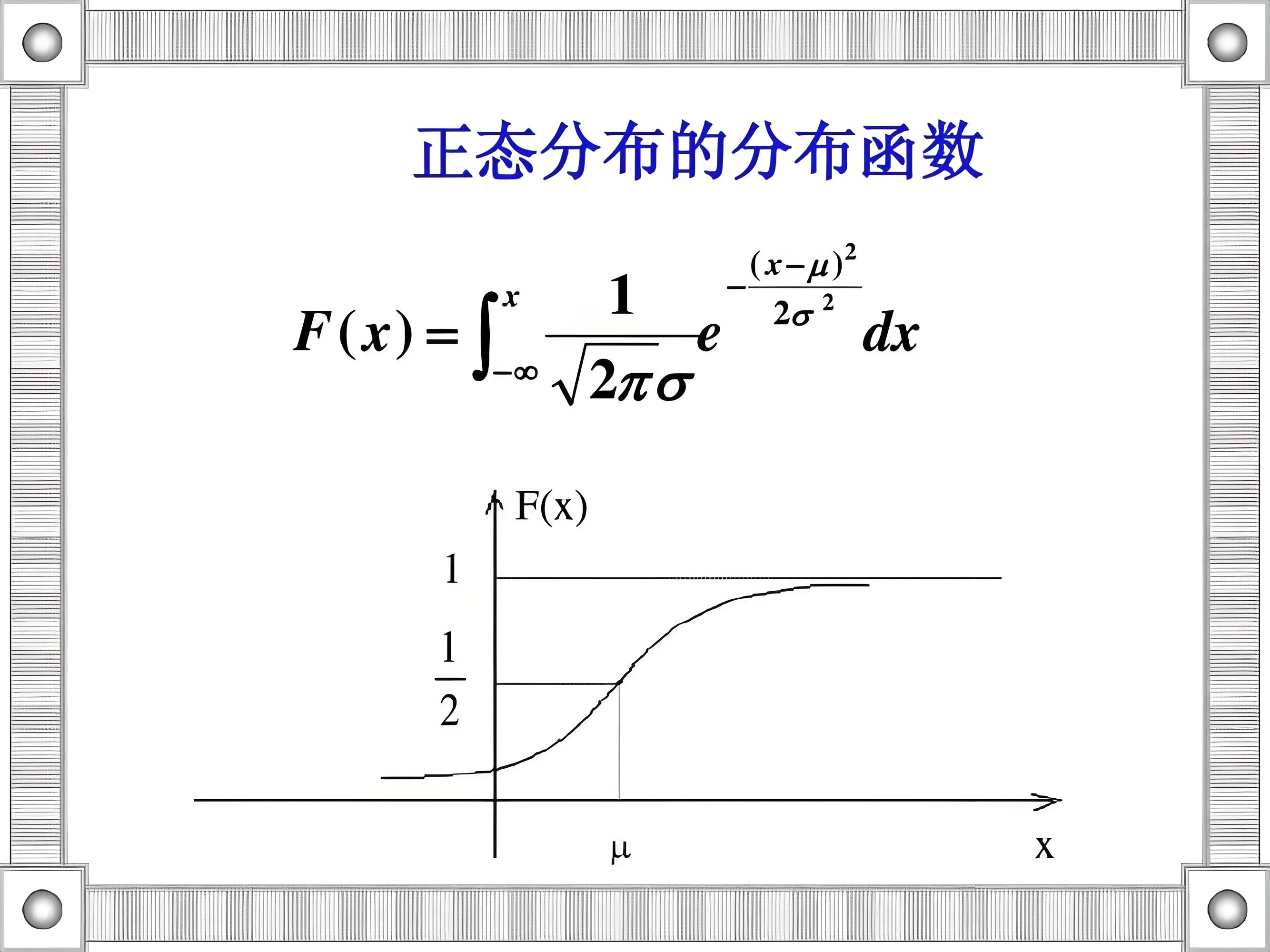
二叉树的输出
先判断边界
深度优先遍历输出
核心思想是递归。按照先根次序、中跟次序、后根次序将value在不同位置输出
1234567891011void out_preorder(node *root){ if (root == nullptr) { return; } cout << root->value << " "; out_preorder(root->left); out_preorder(root->right); delete root;} ...
数据结构与算法A 第九章文件管理和外排序
主存储器和外存储器
计算机存储器是用来存储程序和数据的部件,主要有两种:
主存储器(内存、主存):
随机访问存储器(RAM)
高速缓存 ( cache )
视频存储器 ( video memory )
外存储器(外存):
硬盘 (几百G - 几百T, 1012B )
磁带 (几个P, 1015B )
内存的优缺点:
优点:访问速度快
缺点:造价高,存储容量小,断电丢数据
CPU 直接与主存沟通,对存储在内存地址的数据进行访问时,所需要的时间可以看作是一个很小的常数
外存的优缺点:
优点:价格低、信息不易失 、便携性
缺点:存取速度慢。一般的内存访问存取时间的单位是纳秒,外存一次访问时间则以毫秒或秒为数量级
为了解决存取速度的问题,外存上的数据通常采用分块存取的方式,外存空间被划分为长度固定的存储块,称为“页”,数据以页块作为单位进行存取
文件的组织和管理
文件是存储在外存上的数据结构,是由大量性质相同的记录组成的集合
记录:具有独立逻辑意义的数据块,是文件的基本数据单位
按照记录的类型,文件可以分为两类:
操作系统的文件:一组连续的字符序列,没有明 ...
数据结构与算法A 第八章内排序
排序主要分为两类:内排序和外排序:
内排序:待排序的记录个数较少,整个排序过程中所有的记录都可以直接存放在内存中
外排序:待排序的记录数量太大,内存无法容纳所有记录,在排序过程中还需要访问外存
基于比较的排序方式,时间代价为O(nlogn)
排序问题的基本概念
排序码 (Sort Key):作为排序运算依据的一个或多个域
记录或元素 (Record):结点,进行排序的基本单位
序列 (Sequence):线性表,由记录组成
关键码 (Key):唯一确定记录的一个或多个域,有人翻译为“键”
排序码不一定是关键码,关键码是唯一确定记录的一个域或多个域
排序:将序列中的记录按照排序码顺序排列起来的过程。其中,排序码域的值具有不减(或不增)的顺序。如果排序码不重复,则递增或递减
排序问题:
给定一个序列 R = { r0, r1, …,rn-1 },其排序码分别为 k = { k0, k1, …,kn-1 }
排序的目的:将记录按排序码重排。形成新的有序序列 R’= { r’0, r’1, …,r’n-1 }。相应排序码为 k’= ...
计算机视觉 11 Photometric Stereo
Photometric Stereo
一个3D物体在不同的光照条件下重建法向量,再进一步求解三维
通过在不同照明条件下观察对象的表面法线来估计该对象的表面法线
为什么要估计法向:
法向量与颜色相关
法向量可以得到梯度从而得到平面
输入:使用固定相机和不同的光照条件拍摄多张图像。相机不动,光线改变
Image Intensity
Image Intensity = 𝒇 (Light, Surface Reflectance,Surface Normal)。其中Intensity表示图像颜色,为已知。Light已知。Surface Reflectance反映了物体的材质为未知。Surface Normal为法向量为所求
目标是从约束不足的图像强度中恢复法线
解决歧义性:
多张图片消除歧义性
人为的增加假设或限制
Surface Reflectance
镜面反射(Specular reflection):光线围绕 Surface Normal 反射
漫反射(Diffuse reflection):光线向各个方向均匀散射
此外还有折射、表面 ...
计算机视觉 10 Multi-View Stereo
Multi-View Stereo
和Two-View Stereo的区别:多张图片重建三维而非两张对应的图片
输入:使用校准相机拍摄同一物体或场景的多张图像
任意数量的图像
任意摄像机位置(摄像机网络或视频)
通常校准具有SFM或特殊设备的相机
输出:计算相应 3D 形状的表示。不同于两相机的单视角深度问题,要求重建稠密的3D表达
体素表达:通过0,1控制显示
三角网络表达
点云表达
核心思想:多图片的一致性,稠密的重建要求稠密的一致性
找一个参考图,衡量像素块的相似程度,构建函数图像找到误差最小的进行重建,其中,参考图在其他相机中的对应点都在极线上
Why Multi-View Stereo?(为什么需要多个视角)
对象表面上的不同点在某些相机子集中将更加清晰可见。如果视角不够则可能出现遮挡,倾斜的情况从而导致重建出的3D物体不完整
多视角可以减小误差使得相交区域更小从而形成更强的约束
MVS
Visual Hull based MVS(基于体素)
核心思想:在多个(3个)视角进行拍摄,重建轮廓线:
有像素的部分记为1
没有像素的部分记为 ...
计算机视觉 09 Structure from Motion
Structure from Motion
输入:多张照片
输出:相机的参数以及位置和场景的3D模型
Structure from Motion vs Calibration & Triangulation
Calibration:
输入:从 3D 到 2D 的点对
输出:相机参数
Triangulation:
输入:相机的参数和2D点对
输出:3D点
Structure from Motion
输入:2D到2D的点对
输出:3D点以及相机参数
Structure from Motion: Problem formulation(问题设置)
输入:n 个固定 3D 点的 m 个图像(忽略可见性),使得:Pi是第i个相机的参数,Xj是3D其次坐标,二者均为未知。Xij是第i张图片的投影点
输出:估计 m 个投影矩阵 Pi 和 n 个 3D 点 Xj 来自 mn 对应关系Xij
The Ambiguity of Structure from Motion
SFM有歧义性是不可解的,因此必须加以约束才可解出唯一值,否则会得到一族解。例如下图对同 ...