计算机视觉 05 Image Stitching
Panorama(全景图)
- 全景图的构建方法:
- 提取特征点
- 特征匹配
- 求解变换
- 混合图像
Review: Image Transformations
- Image filtering: change the range of images
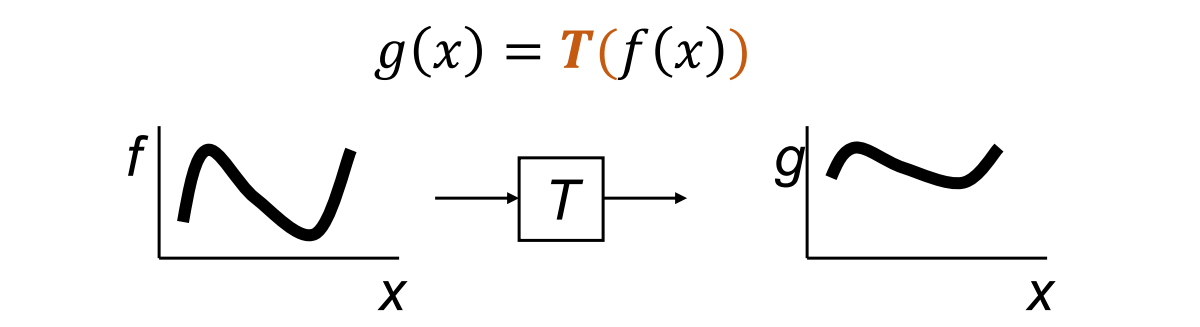
- Image warping: change the domain of images(对定义域变换)
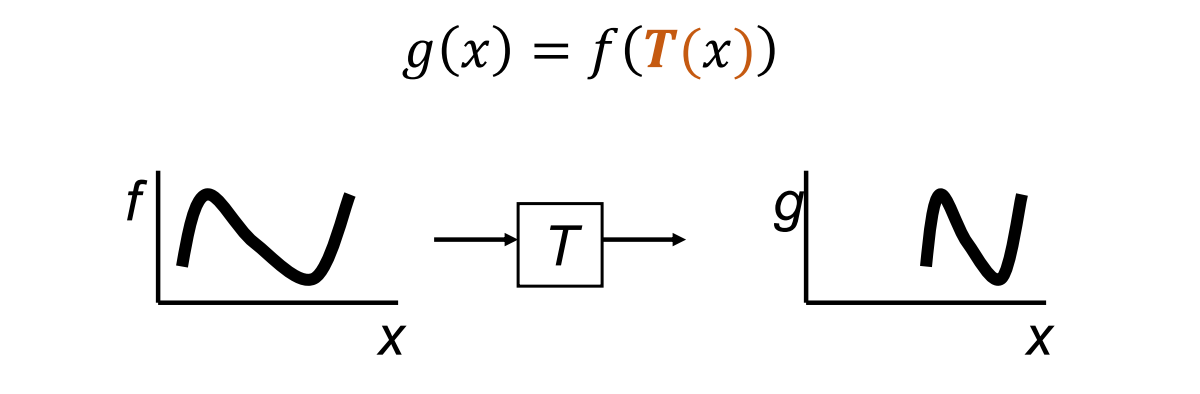
- Examples of Global Image Warping:
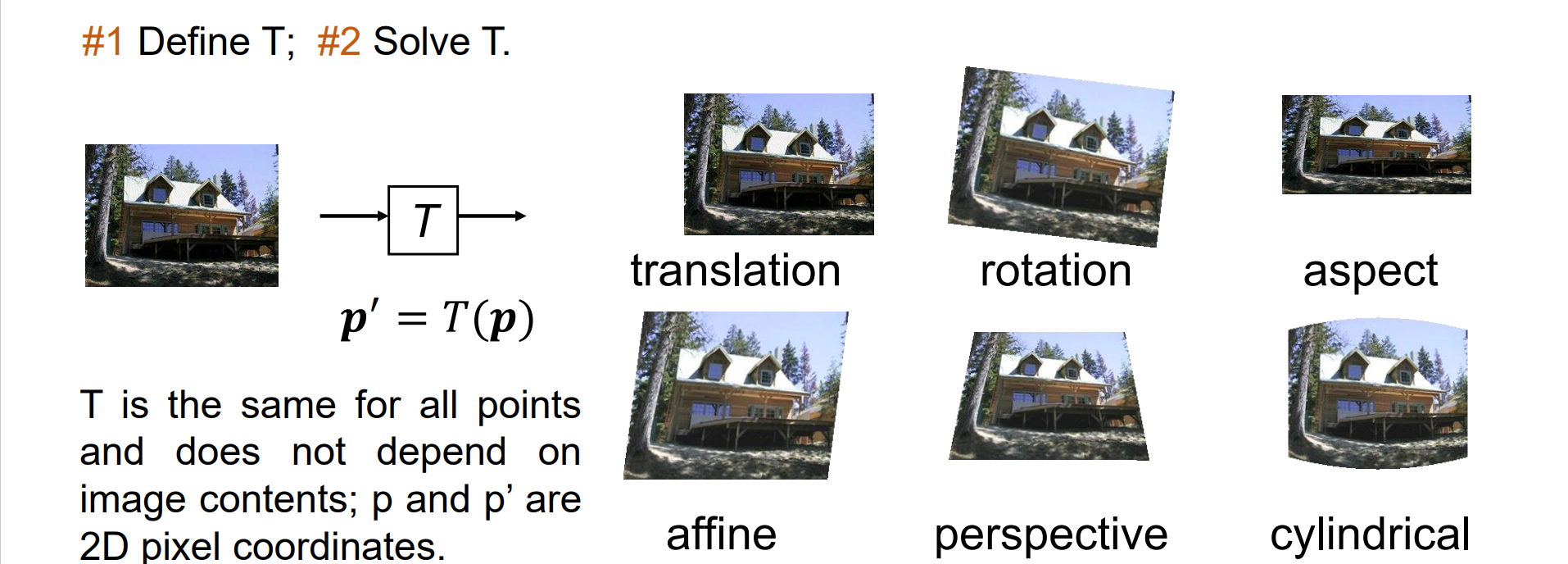
Transformation with Homogeneous Coordinates
- 其次坐标与欧式空间坐标的转换:
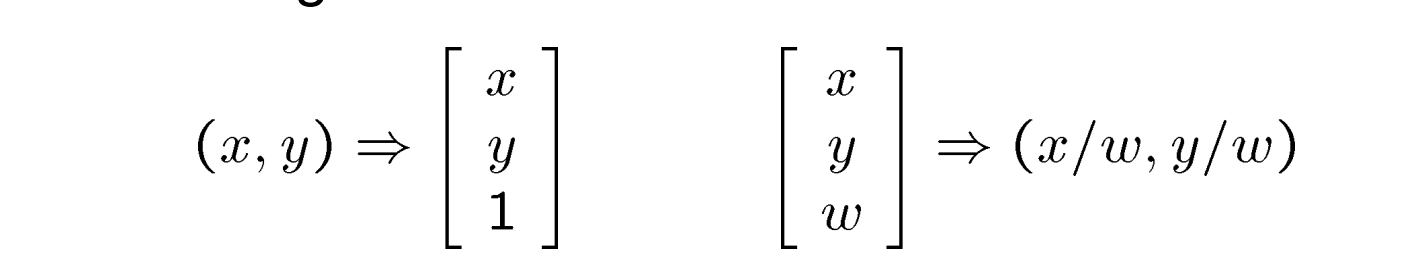
- 线性变换加平移:有6个自由度
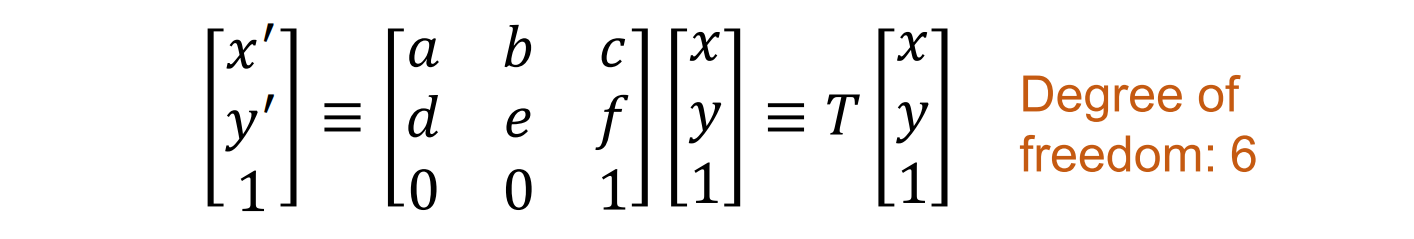
我们得到没有齐次坐标的变换:x’ = Ax + b。其中A = {a,b,c,d},b = {c,f}.T
Examples of Transformations:
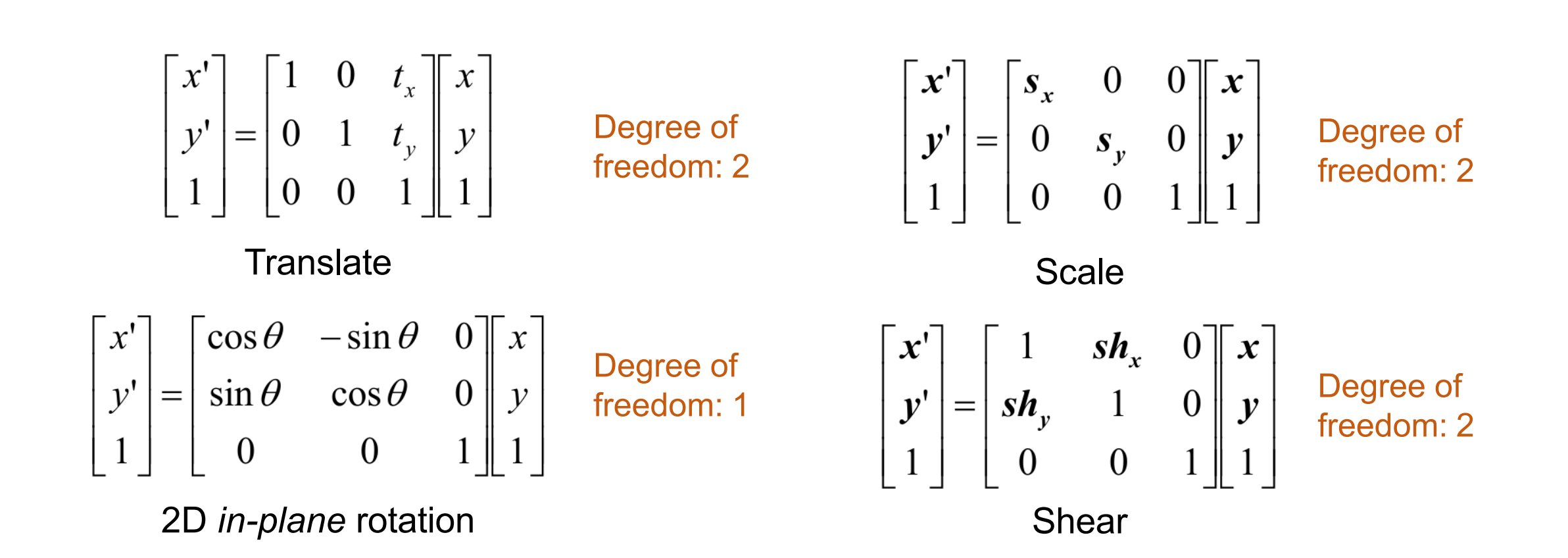
Solve Transformations (#1)
- 给定对应关系:[x’i,y’i] ↔ [xi,yi],则可依照上述理论建立:
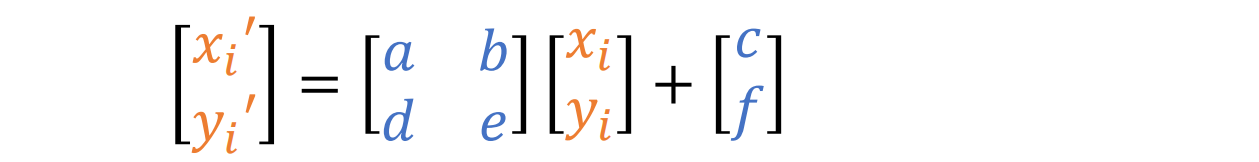
- 此式等价于下面的式子:(将其拉长所得)
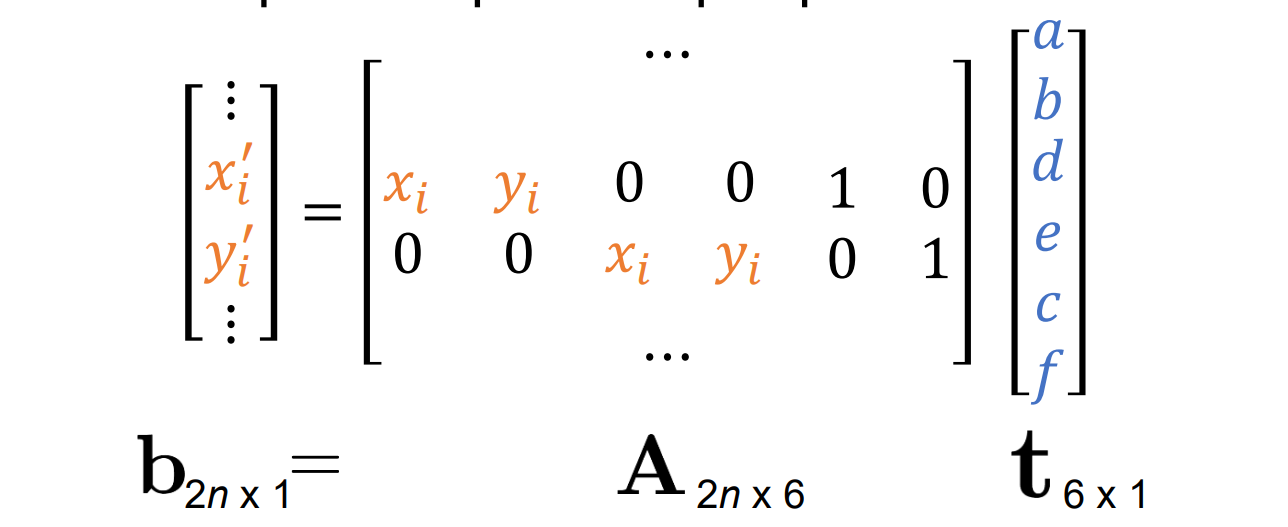
求解变换就是求解t:显然t有6个自由度,每个点形成2个等式,所以需要至少3个不共线的点才能求解t
在实际应用中,我们可以在对应中找到更多的点对。此时通过最小化以下能量函数来寻求最优值:其求解的思想是最小二乘解

- E是二次的,取它的一阶导数,让它为零:
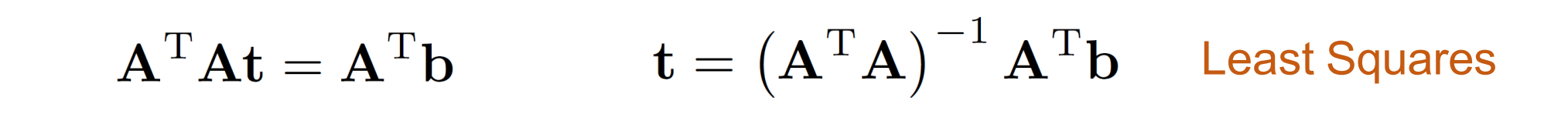
- A.TA一般是满秩的,可求逆解方程
Homography
- 如果两张照片之间不是仿射关系,则不能使用方程:
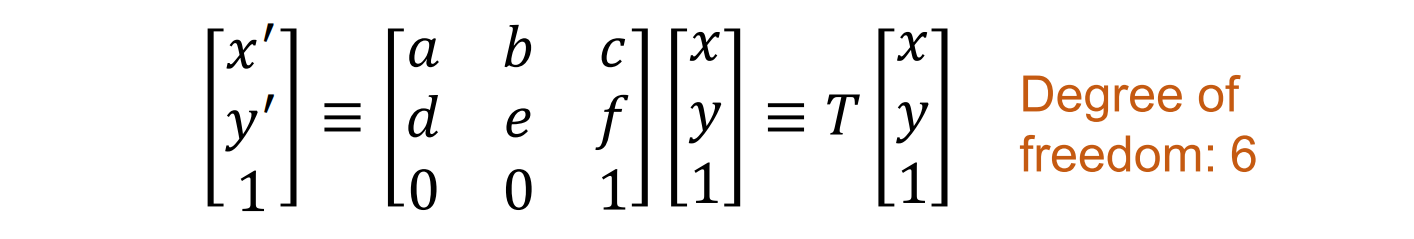
Homography(同源性):Homography也是投影变换。Homography is a 3 × 3 matrix,The last row is [𝑔, ℎ, 𝑖], not [0, 0, 1]
homography的自由度是8,由于每个点能提供两个等式,所以至少需要不共线的四个匹配点
Solve Homographies
- 给出对应:: [x’i,y’i] ↔ [xi,yi],则可建立其次方程:(等比例缩放下相等)
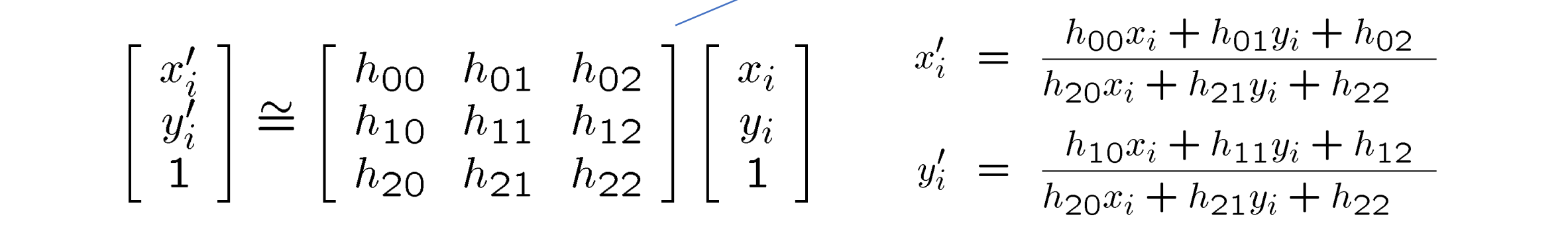
- 求解次方程额两种方法:
- 设h22 = 1
- 设向量长度[h00 h01 … h22] = 1,这种方法数值更加稳定
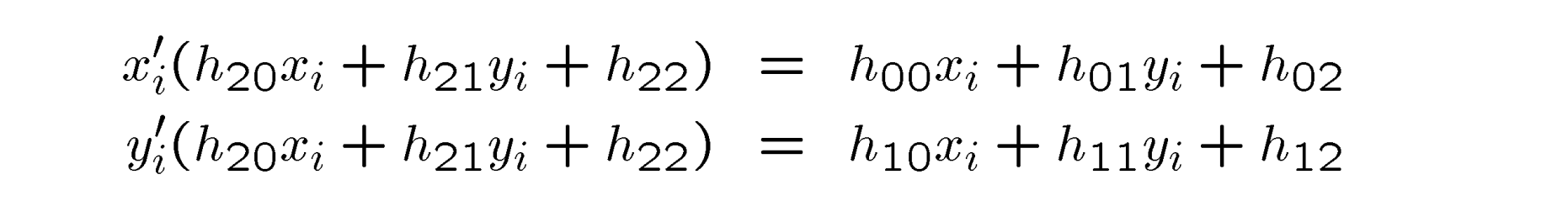
- 写成矩阵形式得:
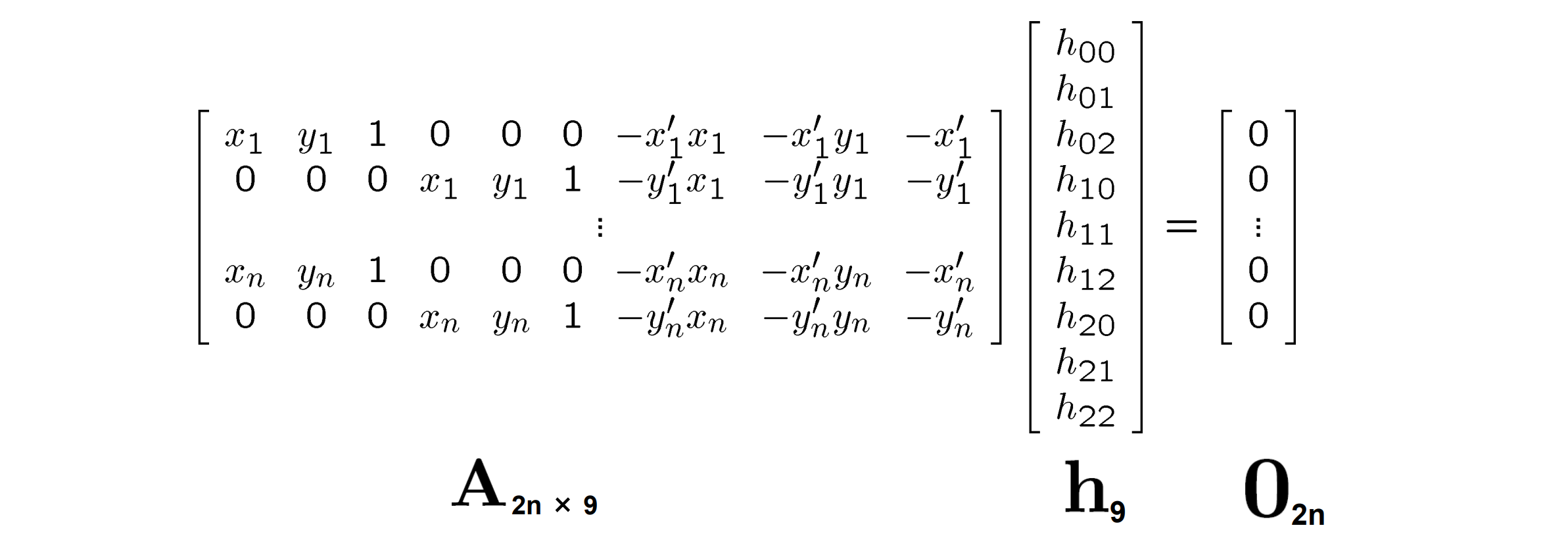
- 在实际应用中,我们可以在对应中找到更多的点对。此时通过最小化以下能量函数来寻求最优值:其求解的思想是特征值。采用第二种方法假设|h| = 1
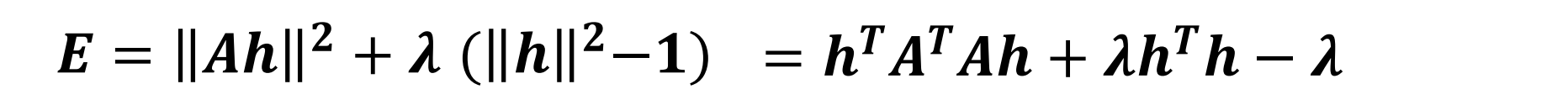
- E是二次的,取它的一阶导数,让它为零:

可知h是A.TA的特征向量中最小的一个
Summary of Solving Homographies
- Build the matrix A according to the homography transformation:
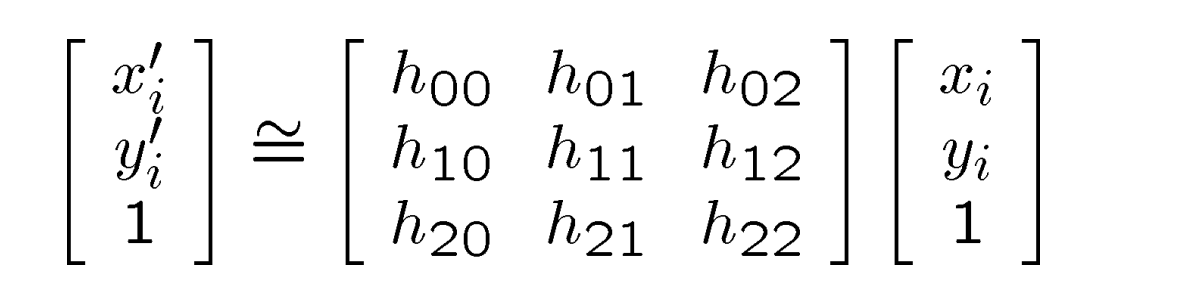

- 计算矩阵A.TA的特征向量并选择最小的特征向量
- Build the matrix A according to the homography transformation:
警告:
- 代数误差:|Ah|²
- 几何误差:
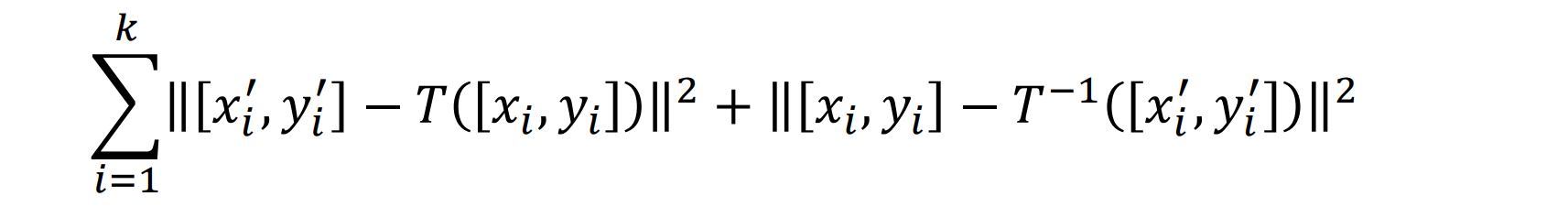
Feature Matching
给定图片A,B,朴素的特征匹配流程如下:
- 计算A和B的特征
- 将 A 和 B 之间的要素与最近的邻域搜索进行匹配
- 计算匹配项集上 A 和 B 之间的homography transformation
问题:Outliers(没有匹配上的点,外点)的影响。L2(范数)能量可能放大outliers的误差,导致误差很大
The key is to eliminate the affect of outliers
RANSAC: Random Sample Consensus
具体步骤如下:
- Randomly choose s samples。Typically s = minimum sample size that lets you fit a model
- Fit a model to those samples。Count the number of inliers that approximately fit the model
- Repeat N times
- Choose the model that has the largest set of inliers
- Fit the model with all inliers
判定内点的方法:设置好模型后,根据噪声多少设置内点的阈值。超过某一阈值则设置为内点
可以使用homography几何误差来判别内点外点:
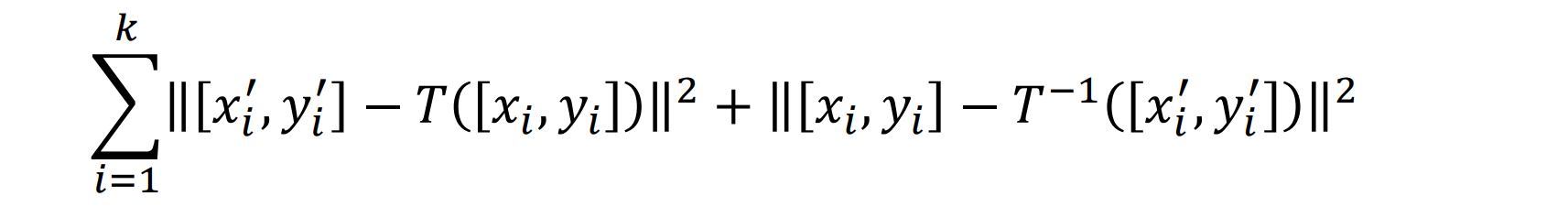
RANSAC终止的时机:
- 迭代次数与异常值的百分比以及我们想要保证的成功概率有关
- 假设内部值的比例为 G,并且模型需要 P 对来拟合,则我们在 N 次迭代后未选择一组内部值的概率为:(1 − G ^P) ^ N。例如如果 G = 50%, P = 4, N = 100, 则 0.5 ^ 4 = 0.0625, (1 − 0.5 ^ 4) ^ 100 = 0.00157
- 如果我们想要最多为 e 的失败概率,那么:

RANSAC的优缺点:
- PROS:
- Simple and general
- Applicable to many problems
- Often works well in practice
- CONS:
- Has parameters to tune
- May fail for low inlier ratios
- Requires too many iterations
- Other methods to deal with outliers:Robust statistics(鲁棒统计)
- PROS:
Image Blending
Review: Image Blending with Laplacian Pyramid


Poisson Image Editing
问题:源图像的色调与目标图像不兼容
解决问题的关键思想:应保留源图像的梯度:其中,g是原图像,f*是目标图像,f是输出图像,Ω是图像融合的区域
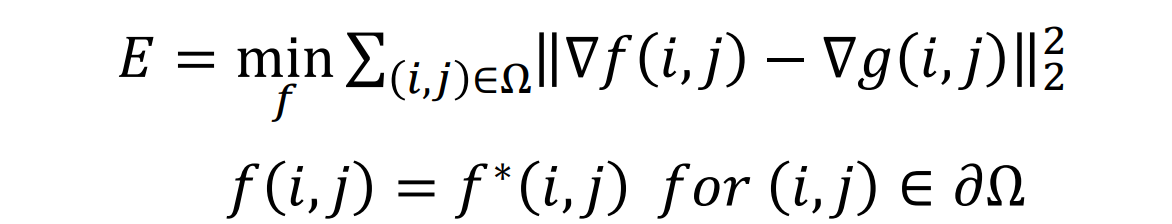
- 解决优化问题的方法:先写成矩阵形式,再利用最小二乘法求解
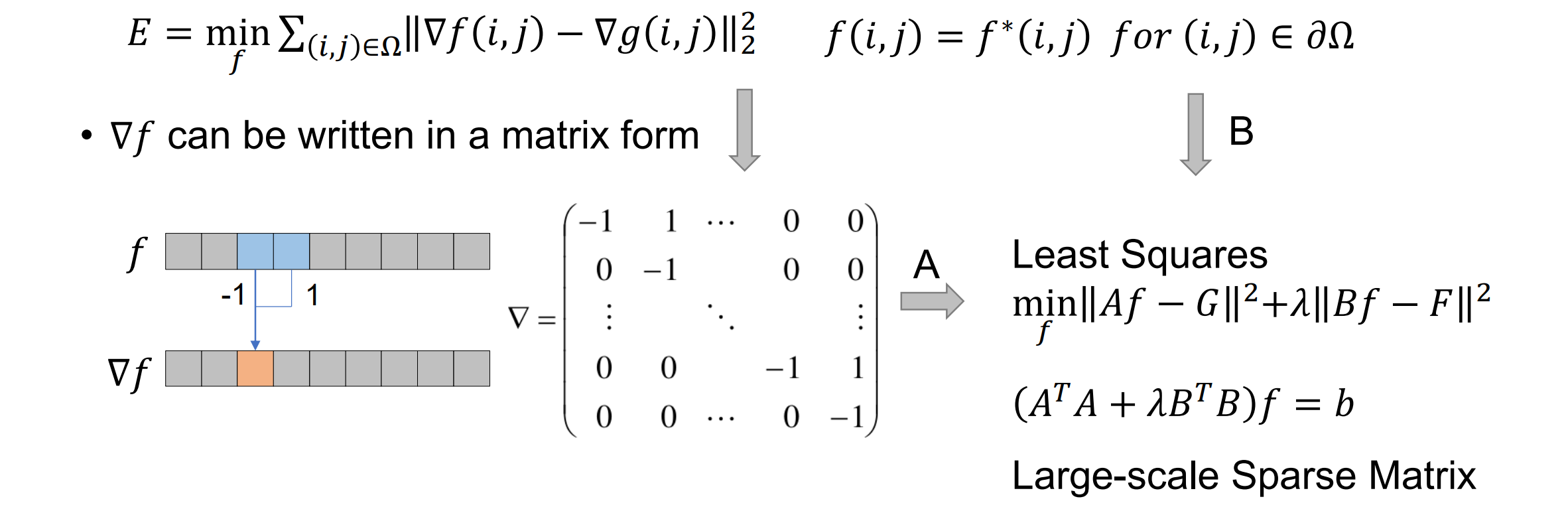
- Poisson Image Editing for Panorama:
- Solve the homography
- Warp the source image to the reference image
- Warp the mask image to the reference image
- Run the Poisson Editing algorithm by keeping the gradient in the mask region


