Two-View Stereo(双视图立体)

  • 用两个相机解决单一视角的模糊性：Stereo: use 2 calibrated cameras in different views and correspondences

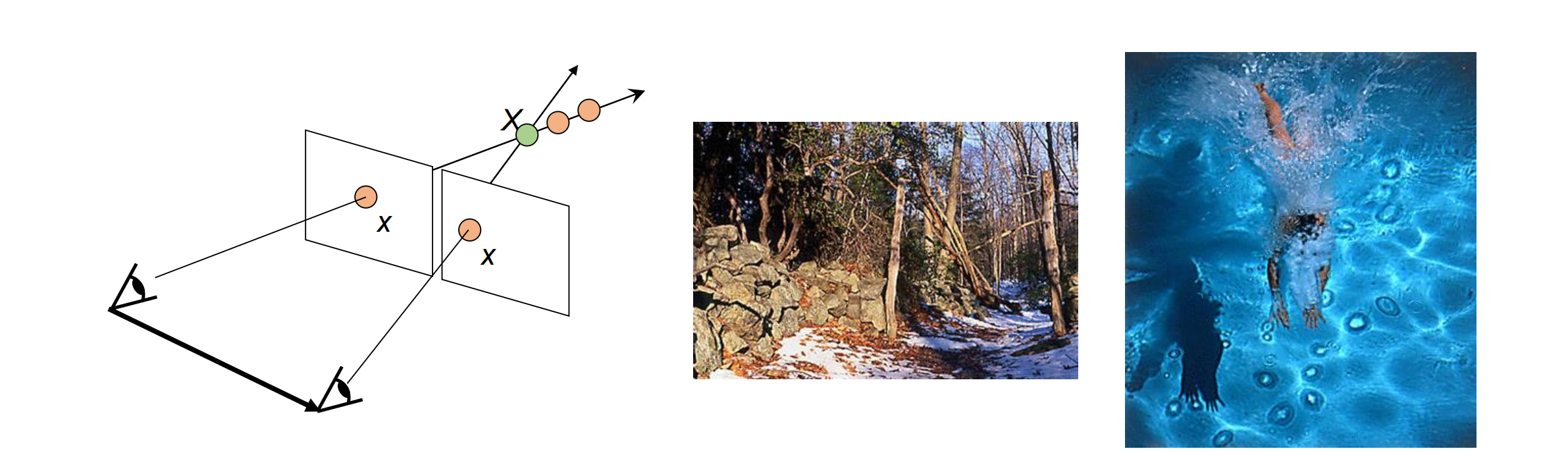
image.png

Typical 3D Reconstruction Pipeline

image.png

Review: Camera Calibration with a Single Camera

  • 两台相机的设置能否提供更多校准功能？

  • Camera Calibration 所需：

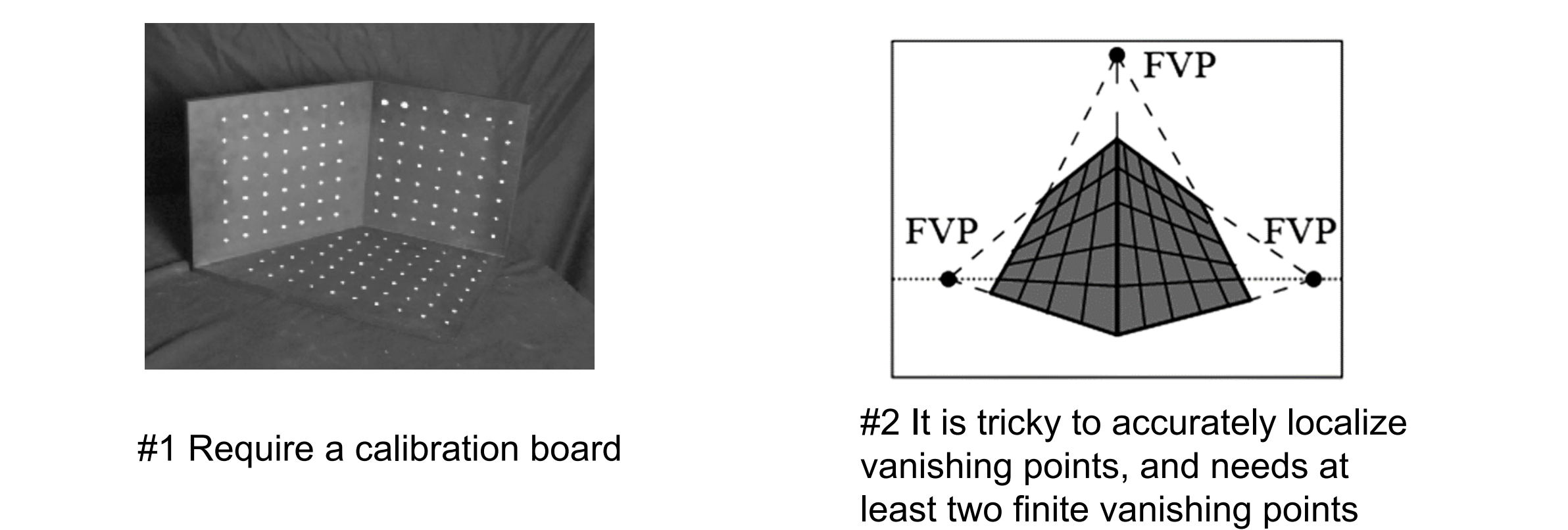
    1. 需要校准板
    2. 准确定位消失点很棘手，并且至少需要两个有限的消失点
      image.png

Review: Triangulation

  • 问题设置：给定一个 3D 点在两个或多个图像（具有已知相机矩阵）中的投影，找到该点的坐标

  • 两台相机的设置能否为 3D 估计提供更多功能？

Two-view Stereo: Key Idea

  • 考虑相机中心和视觉光线到另一个视图中的投影，而无需明确的 3D 推理

  • 可以校准两台相机

  • 可以找到约束条件，以便更轻松地对应和 3D 重建

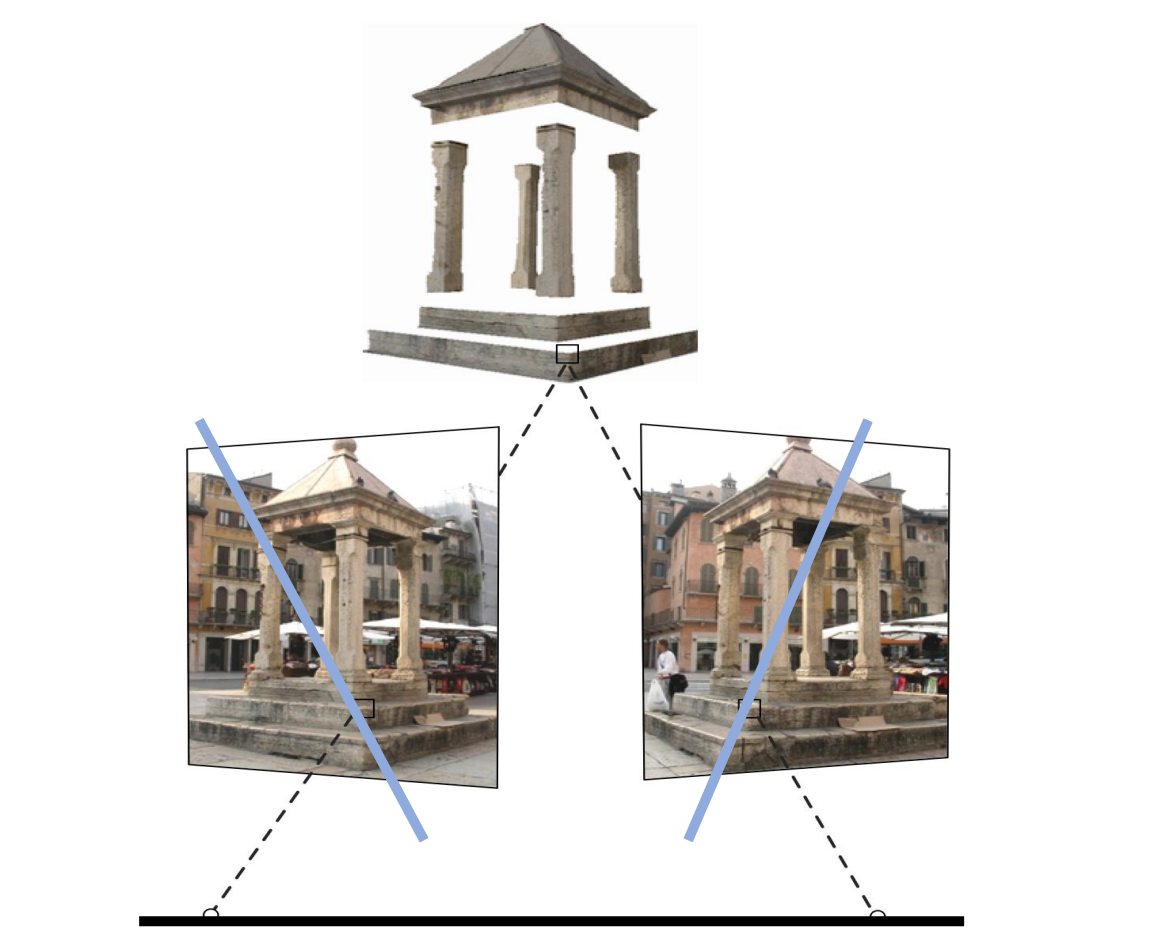
  • 如下图：对应的点在固定的线上

image.png

Epipolar Geometry(极点几何)

  • 假设我们有两台中心为 O、O′ 的相机，基线(baseline)是连接原点的线

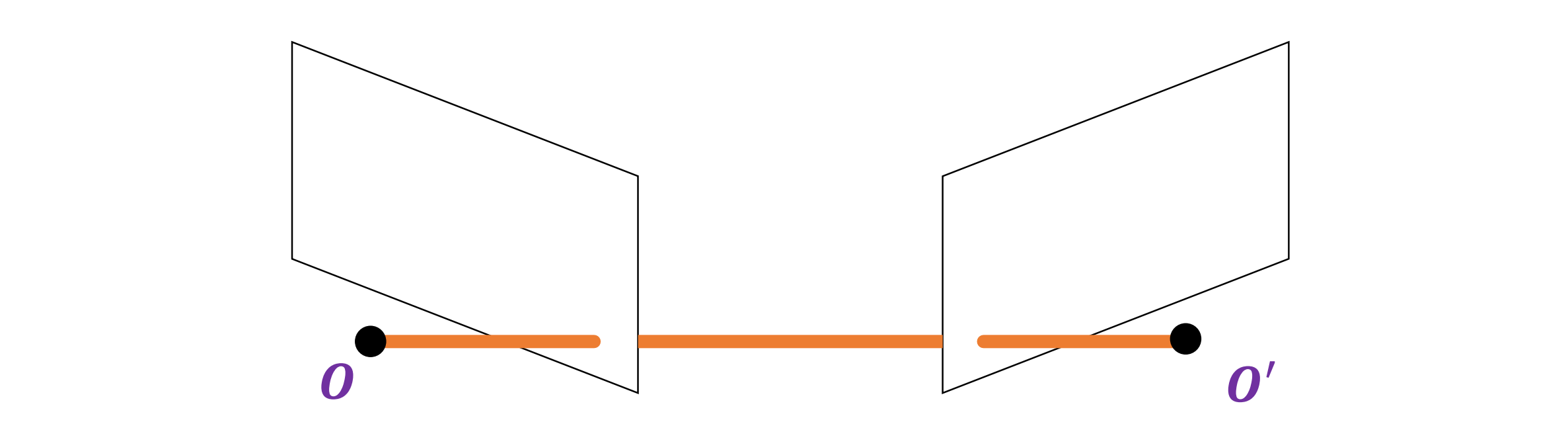
image.png

  • 极点(Epipolar) e、e’ 是基线与图像平面相交的位置，或每个视图中其他相机的投影

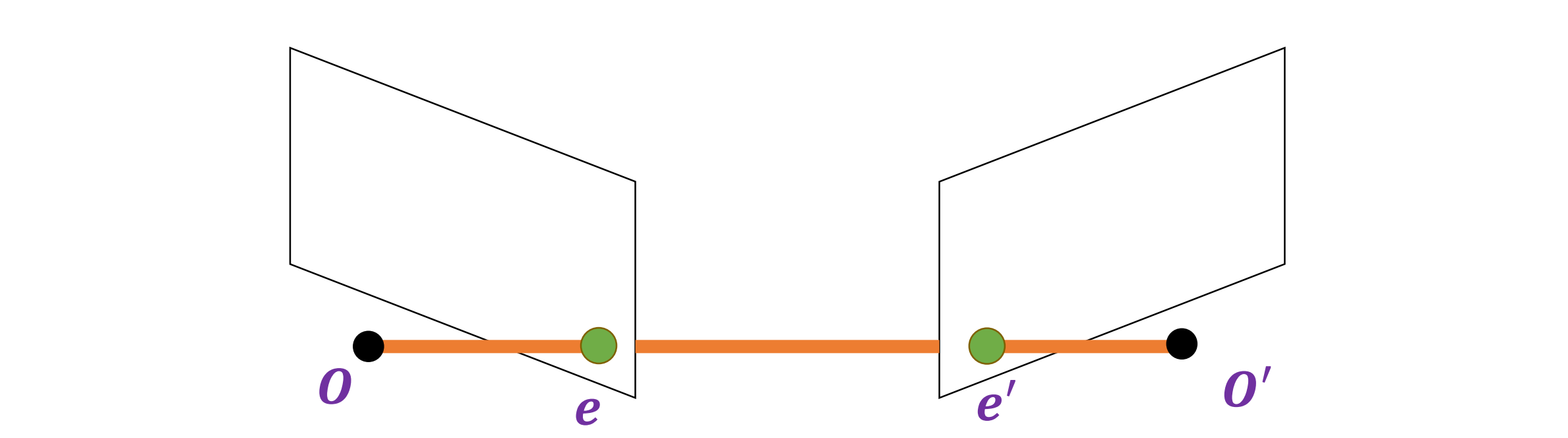
image.png

  • 考虑一个点 X，它投影到 x 和 x′。由 X、O 和 O′ 形成的平面称为极平面(epipolar plane)，有一族平面穿过 O 和 O′

  • 极线(epipolar lines)将极点与X的投影点相连。极线是极平面与图像平面的交点——它们成对出现

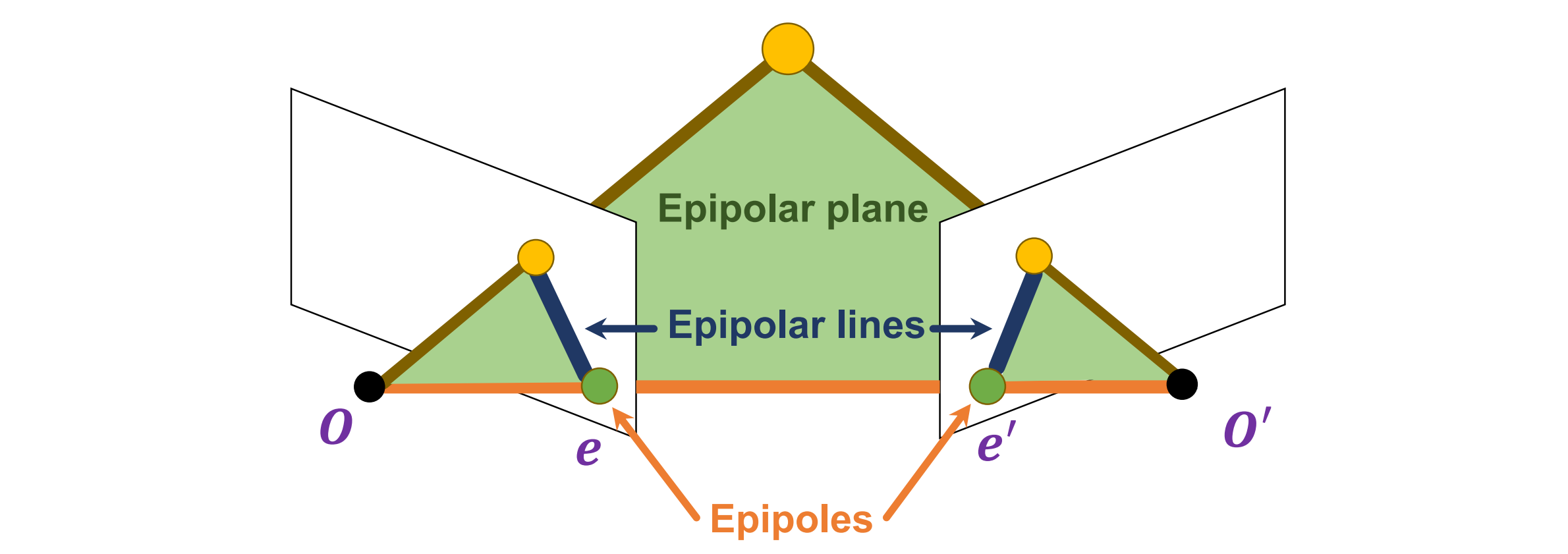
image.png

Example Configuration #1: Converging Cameras(汇聚相机)

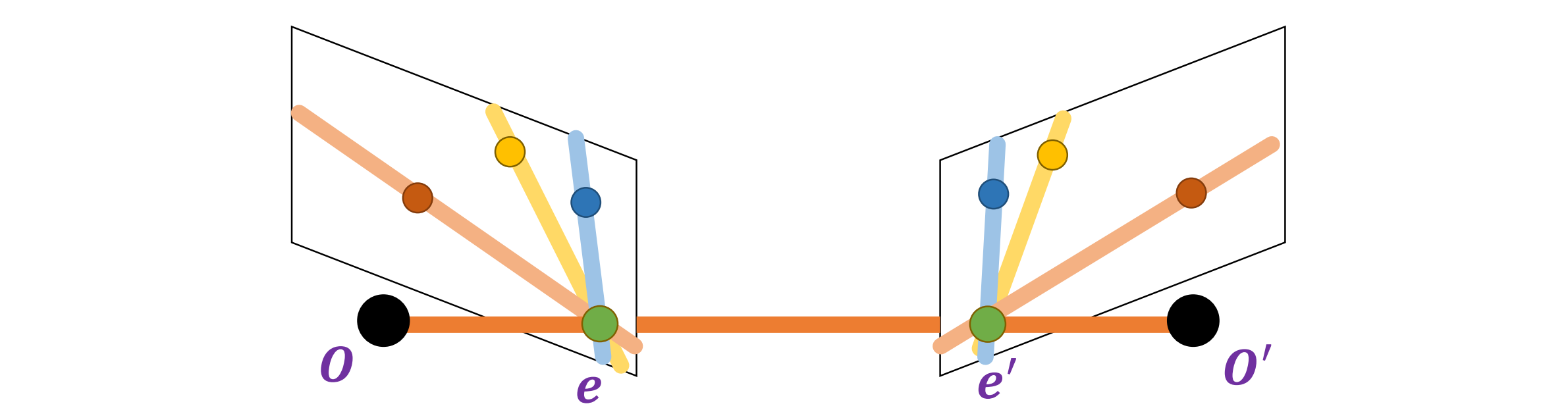
image.png

  • 极点是有限远的，在图像中可能可见或不可见，同一个三维点的投影见下图：

image.png

Example Configuration #2: Parallel to Image Plane(平行于图像平面)

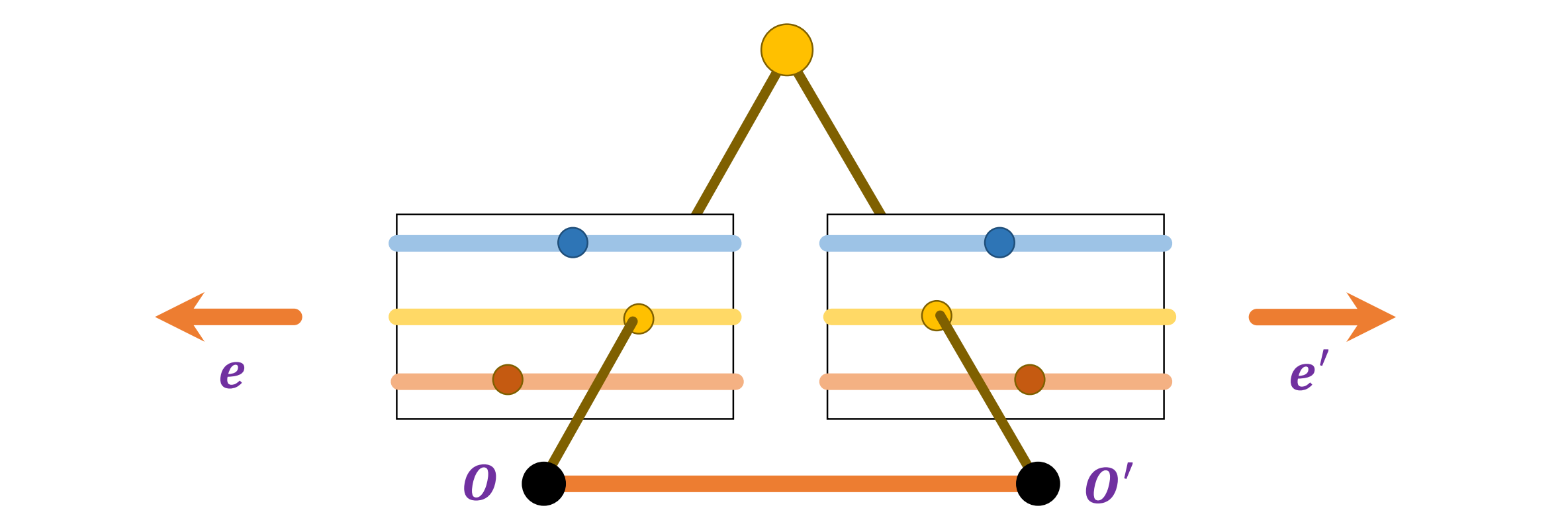
image.png

  • 极点无限远，极线平行的情况：

image.png

Example Configuration #3: Motion Perpendicular to the image plane(垂直于图像平面的运动)

  • Epipole与相机的主轴重合:

image.png

Essential Matrix & Fundamental Matrix

极点约束(epipolar constraint)

  • 数学上描述极点约束：考察一张图像中的单个点 x。与另一张图片中的 x 对应的 x′在哪里？沿对应于 x 的极线 （将 O 与 x 连接的可见光线投影到第二个图像平面）

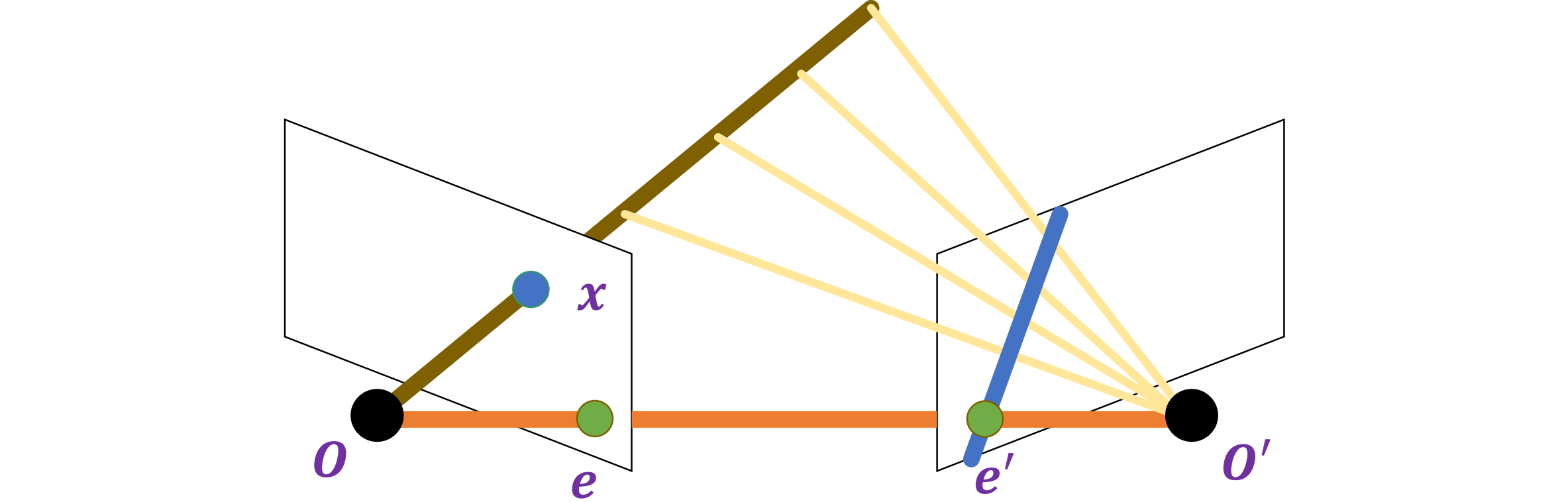
image.png

  • 同样，左图中对应于 x′ 的所有点都必须位于对应于 x′ 的极线上

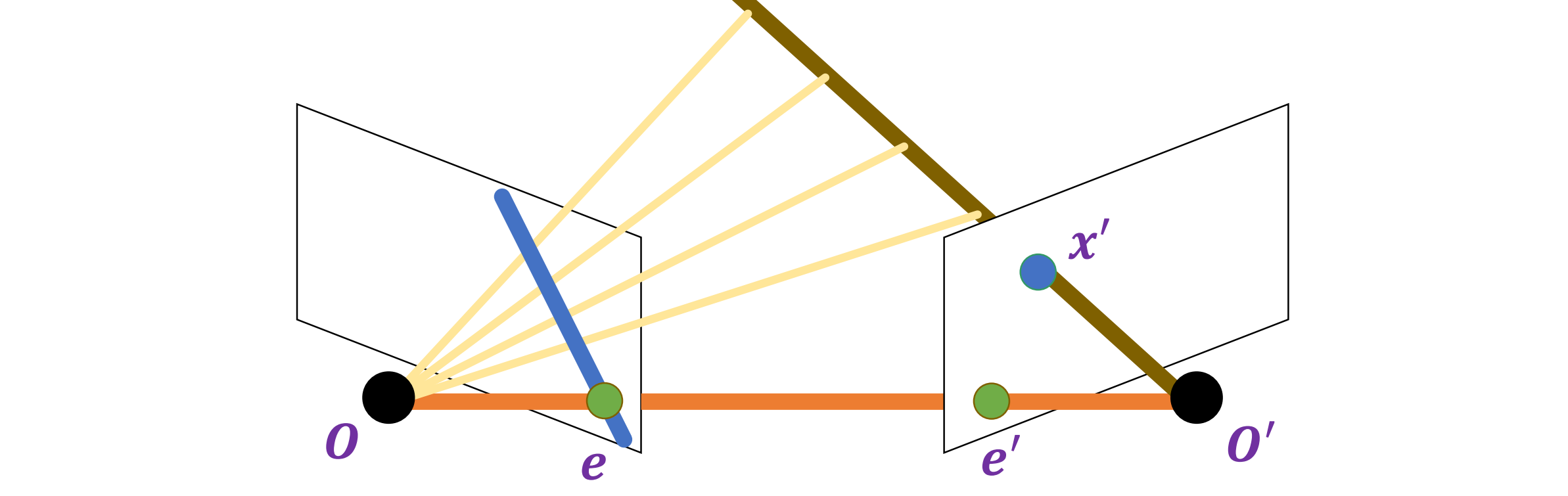
image.png

  • x 的潜在匹配必须位于匹配的极线上 l′,x’ 的潜在匹配必须位于匹配的极线l上

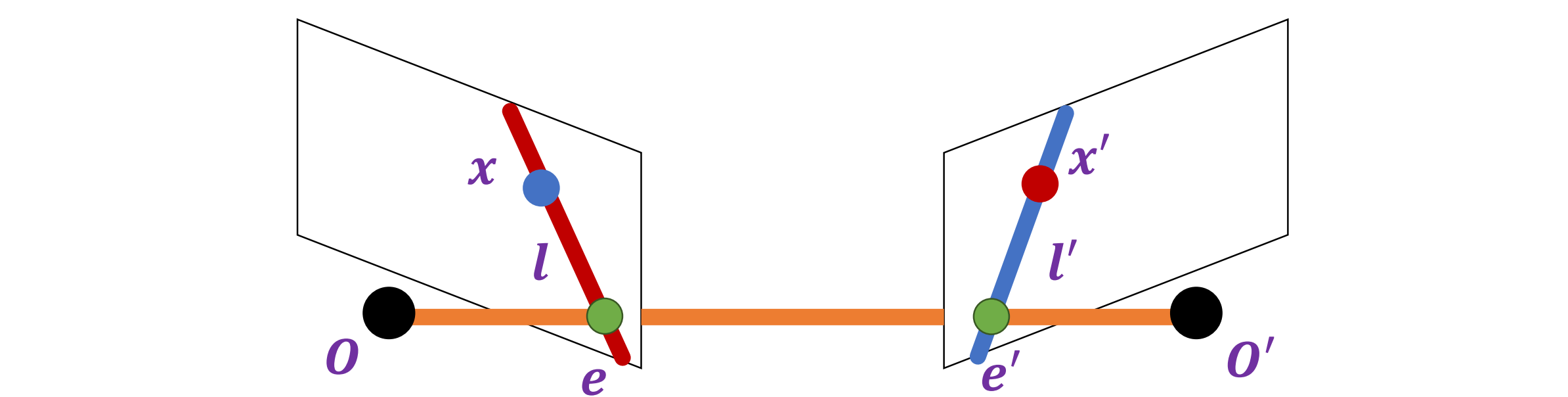
image.png

  • 例如下图：左侧图像中的点x所对应的点一定分布在右侧图像中的直线上(epipolar line)

image.png

  • 每当两个点 x 和 x′ 位于匹配的极线 l 和 l′ 上时，与它们对应的可见光线在空间中相遇，即 x 和 x′ 可以是同一 3D 点 X 的投影。相交点一定投射到极线上，极线上的点不一定投影到交点 x

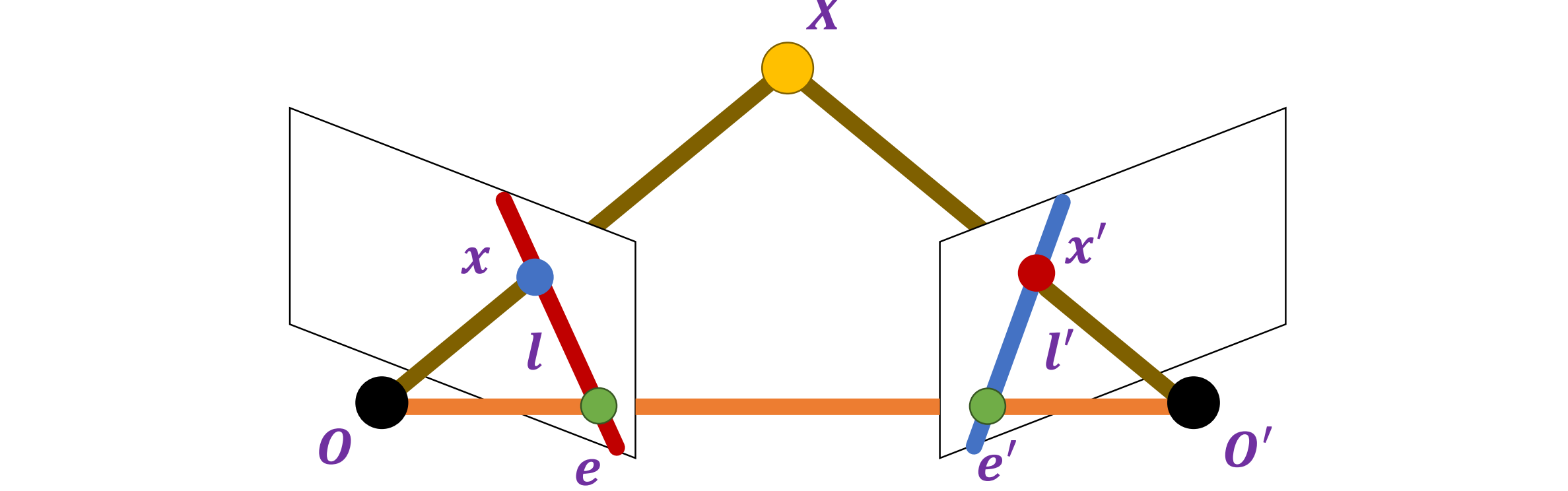
image.png

  • 警告：如果 x 和 x′ 满足极点约束，这并不意味着它们必须是同一 3D 点 X 的投影

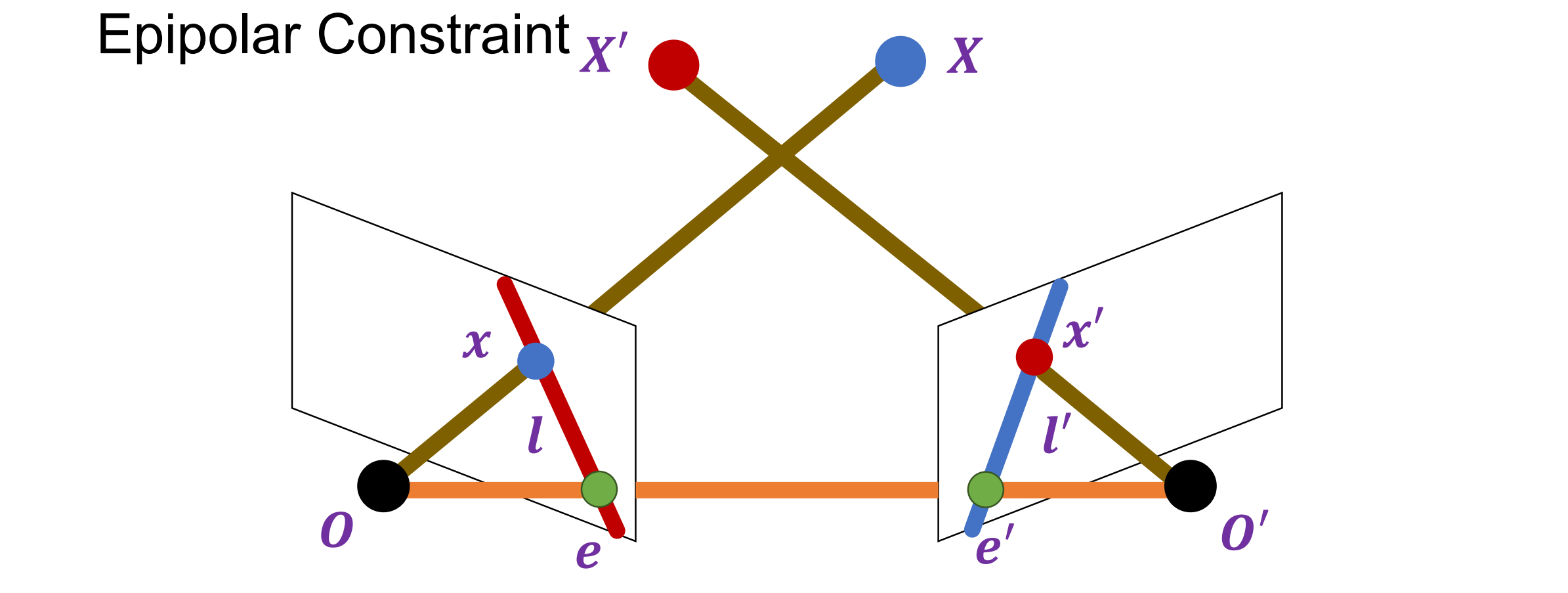
image.png

  • 一般来说，由于噪声和不准确的校准，两条光线在空间中不会完美相交

Epipolar Constraint: Calibrated Case(校准情况)

  • 假设相机固有参数已知，并且世界坐标系设置为第一个相机的坐标系。给出投影矩阵K[I | 0] 和 K′[R | t] (内参矩阵)，R,t可以表示两相机间的相对关系

  • 可以将投影矩阵和图像点乘以逆校准矩阵，得到归一化图像坐标：其中前者是像素坐标，后者是归一化的像素坐标

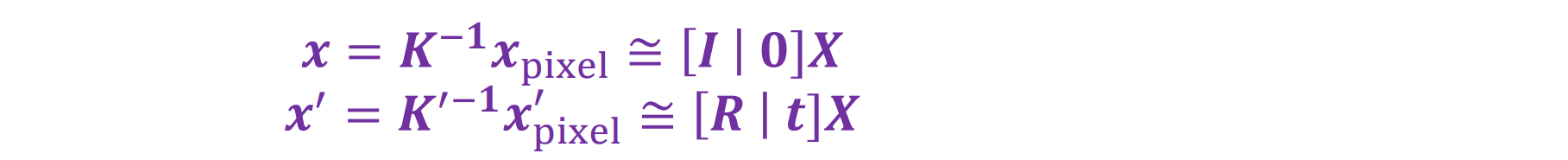
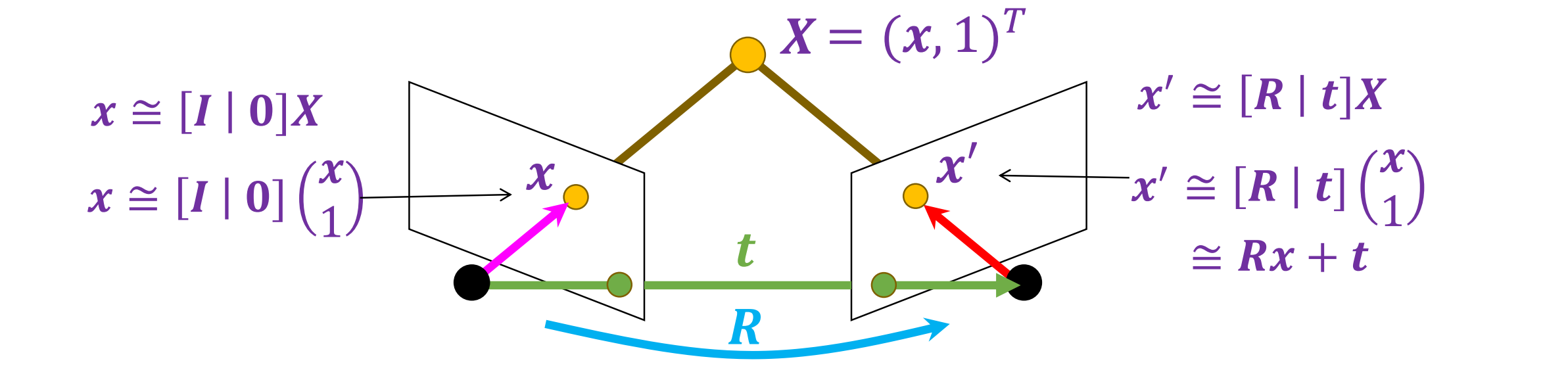
image.png

image.png

  • 将三维点投影至x可得x’ ≌ Rx + t,说明向量x’,Rx和t是线性相关的

  • 这个约束可以使用 triple 积来写：𝒙′ ∙ [𝒕 × 𝑹𝒙] = 0，即给定的三个向量定义的平行六面体的（有符号）体积

  • 将叉乘改为矩阵乘法，设E = [tx] R 可得一个二次型。其中 E 是 Essential 矩阵，表示了两个相机之间平移或旋转的关系

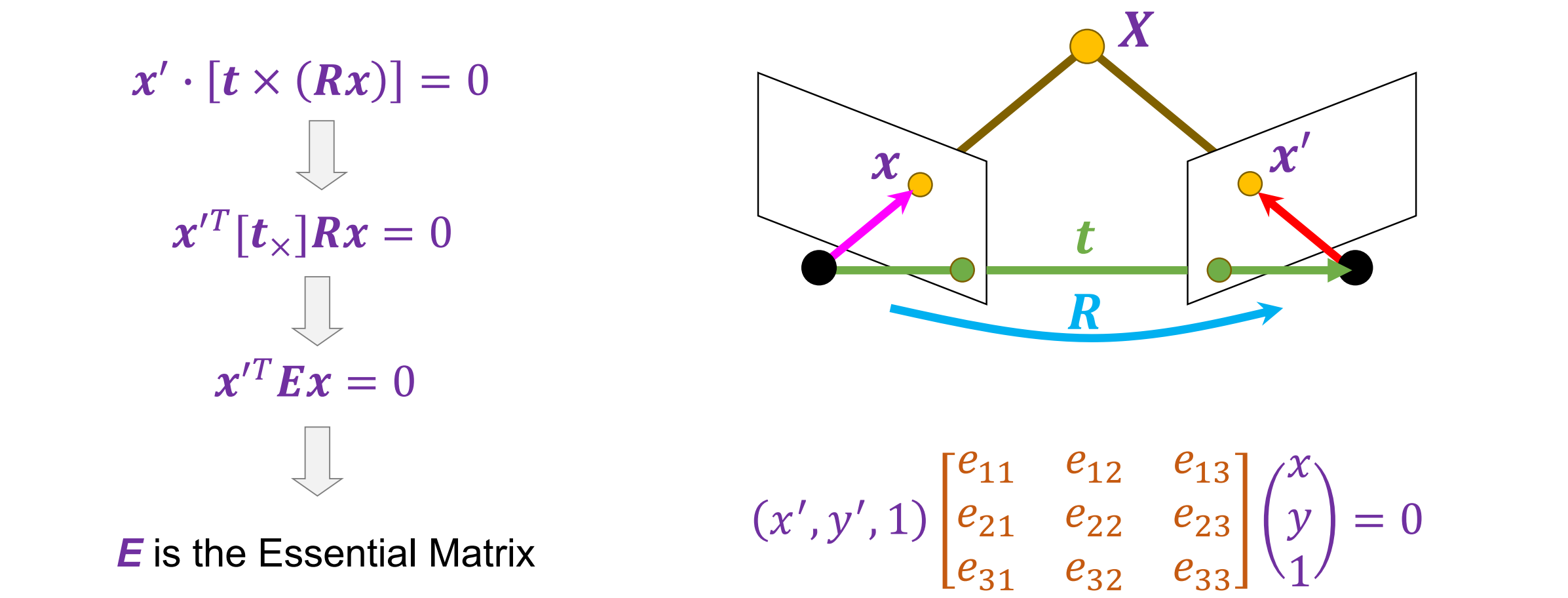
image.png

  • 与 x 相关的epipolar line(过 x’ 的epipolar line)的方程：𝒙′.𝑇𝑬𝒙 = 𝒙′.𝑇𝒍′= 𝟎, 𝑤ℎ𝑒𝑟𝑒 𝒍′= 𝑬x

  • 与 x’ 相关的epipolar line(过 x 的epipolar line)的方程：𝒙′.𝑇𝑬𝒙 = 𝒍.𝑇𝒙 = 𝟎, 𝑤ℎ𝑒𝑟𝑒 𝒍 = 𝑬.𝑻𝒙′

  • 进一步推得Ee = 0;E.Te’ = 0,e是极点

  • 𝑬 is singular with a rank of 2：

    1. [tx]的秩为2
    2. R的秩为3

  • 𝑬 has 5 degrees of freedom

    1. 平移矩阵：3个自由度
    2. 旋转矩阵：3个自由度
    3. 等比例缩放减少一个自由度

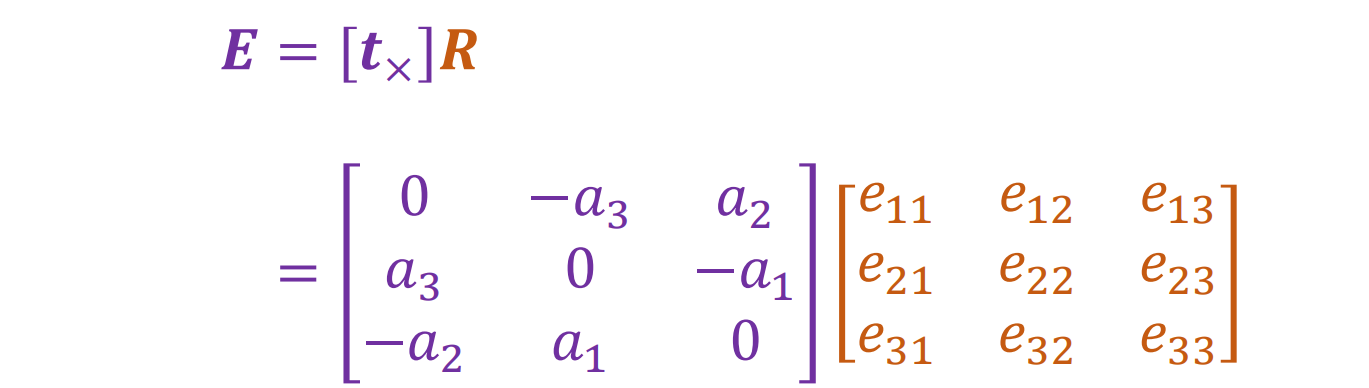
image.png

Epipolar Constraint: Uncalibrated Case(未校准的情况)

  • 假设两台相机的校准矩阵 K 和 K′ 未知，归一化坐标而言的极点约束是：

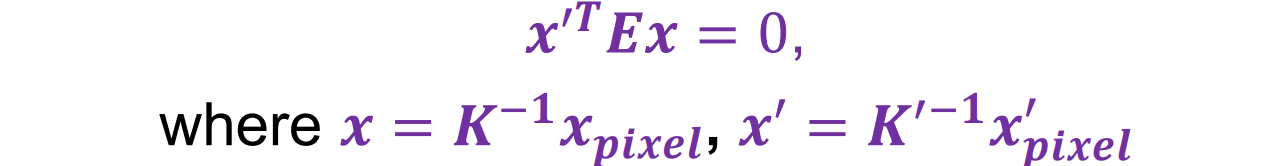
image.png

  • 可以得到如下限制：

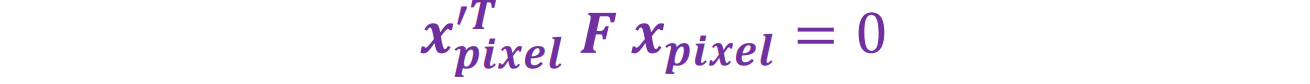
image.png

image.png

  • 内参外参旋转平移，y坐标相同时找对应点扫描线并且计算深度

  • 与 x 相关的epipolar line(过 x’ 的epipolar line)的方程：𝒙′.𝑇F𝒙 = 𝒙′.F𝒍′= 𝟎, 𝑤ℎ𝑒𝑟𝑒 l′= Fx

  • 与 x’ 相关的epipolar line(过 x 的epipolar line)的方程：𝒙′.𝑇F𝒙 = 𝒍.𝑇𝒙 = 𝟎, 𝑤ℎ𝑒𝑟𝑒 𝒍 = F.𝑻𝒙′

  • 进一步推得Fe = 0;F.Te’ = 0,e是极点

  • F is singular with a rank of 2：

    1. [tx]的秩为2
    2. R的秩为3
    3. K满秩

  • F has 7 degrees of freedom

    1. 平移矩阵：3个自由度
    2. 旋转矩阵：3个自由度
    3. K:3个自由度
    4. 等比例缩放减少一个自由度
    5. Det(F) = 0

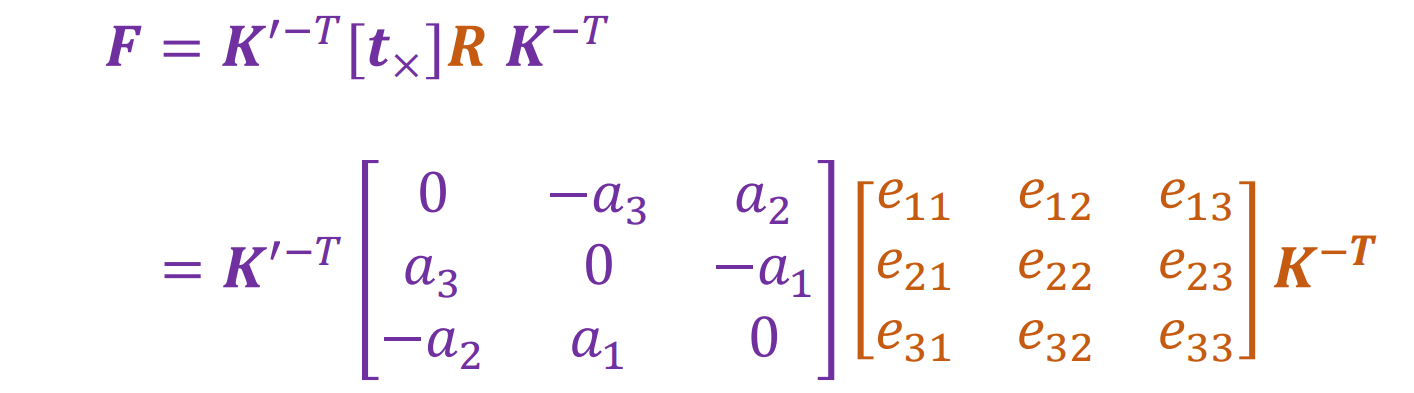
image.png

Estimating the Fundamental Matrix

  • Find correspondences 𝒙 = (𝑥, 𝑦, 1).𝑇 and 𝒙′= (𝑥′, 𝑦′, 1).T,找到两个对应点

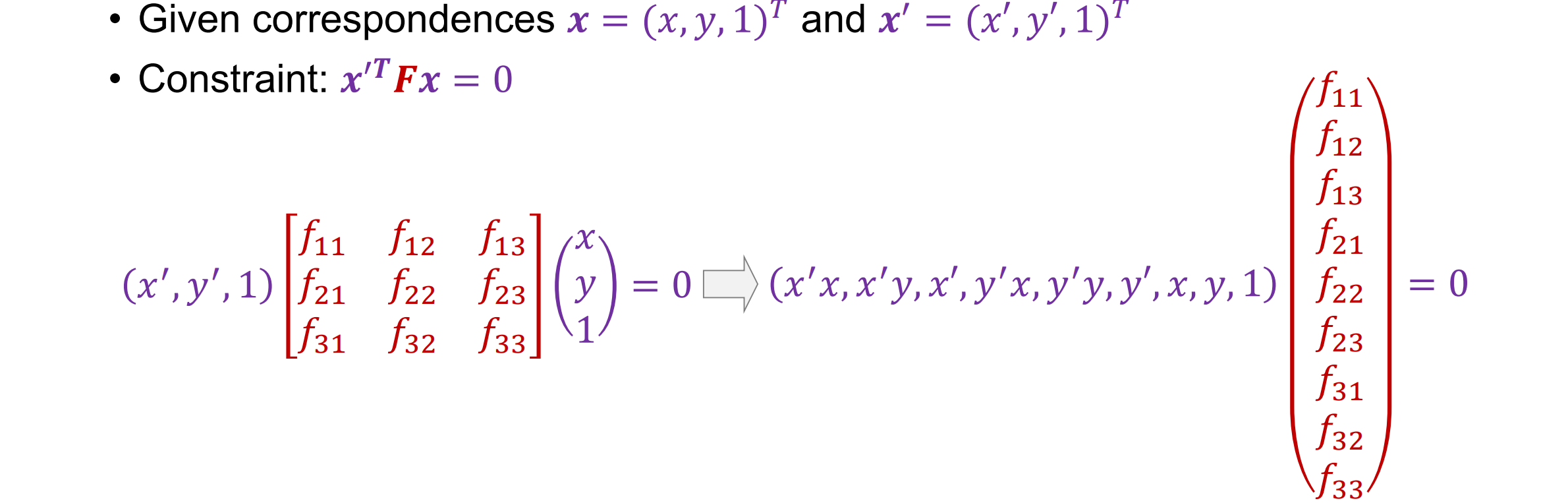
image.png

image.png

Eight-Point Algorithm

image.png

  • 其中u是一堆配对点。f模长为1时优先约束，U.TU的特征值最小的特征向量为所求

Enforcing the Rank-2 Constraint(实施rank-2约束)

  • 𝑭 needs to be singular/rank 2

  • SVD decomposition: 𝑀𝑚×𝑛 = 𝑈m×𝑚 ⋅ Σ𝑚×𝑛⋅ 𝑉.T𝑛×n

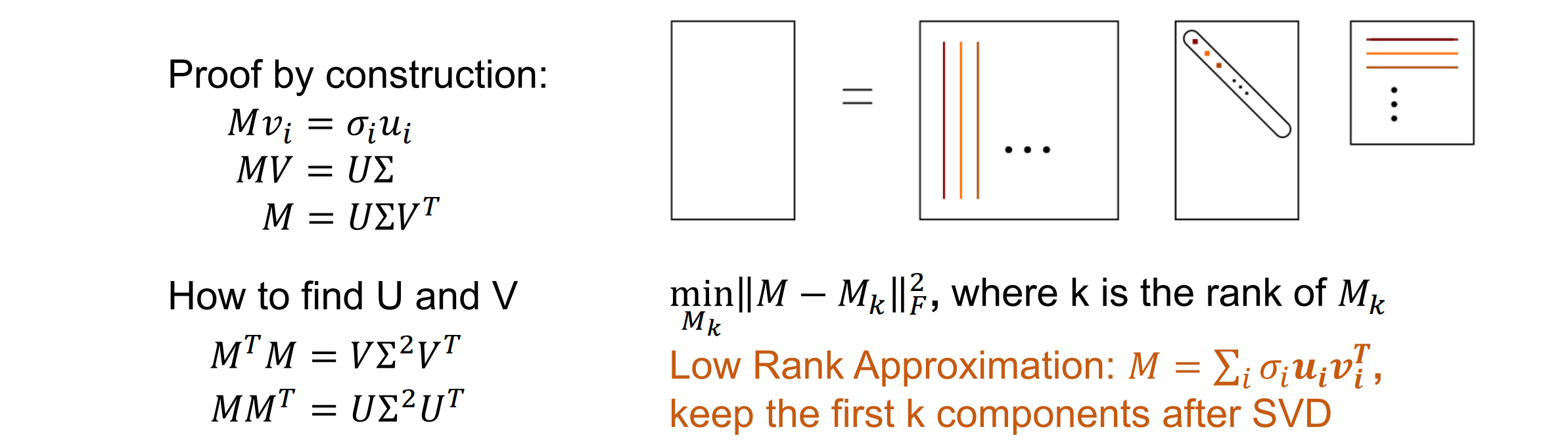
image.png

  • 秩k对M的逼近，找到前k个最大的奇异值

  • 解决方案：取初始估计值的 SVD 并丢弃最小的奇异值

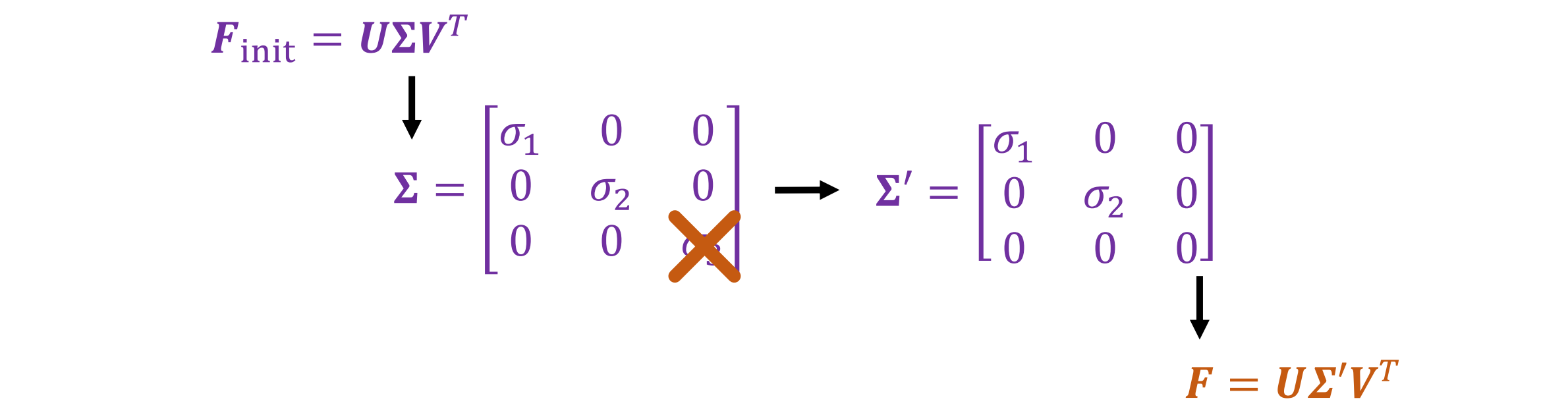
image.png

image.png

Normalized Eight-Point Algorithm

  • 回想一下 x， y， x’ ， y’ 是像素坐标。U 的每一列的数量级可能是多少——这会导致数值不稳定

image.png

  • Normalized Eight-Point Algorithm的流程：
    1. 在每个图像中，将点集以原点为中心，并对其进行缩放，使原点和点之间的均方距离为 2 像素
    2. 使用八点算法从归一化点计算 F
    3. 通过 SVD 分解强制执行 rank-2 约束
    4. 将基本矩阵转换回原始单位：如果 T 和 T′ 是两个图像中的归一化变换，则原始坐标中的基本矩阵是 T′.TFT

Nonlinear Estimation of the Fundamental Matrix

  • 以前的线性方法最小化了点 xi ′ 和外极线 Fxi（或点 xi 和极线 F.Txi ′）之间的平方代数距离之和：

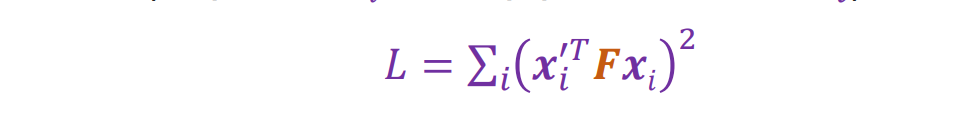
image.png

  • 非线性方法使几何距离的平方和最小:

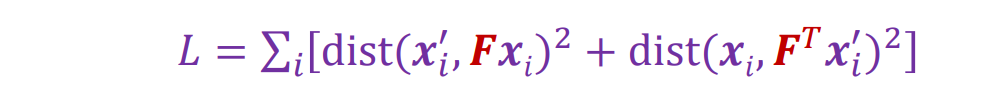
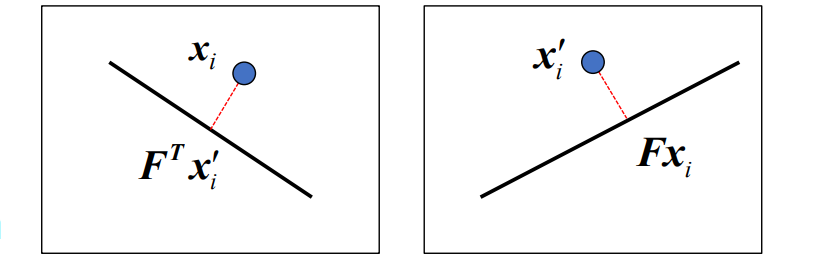
image.png

image.png

Fundamental Matrix and Epipolar Lines

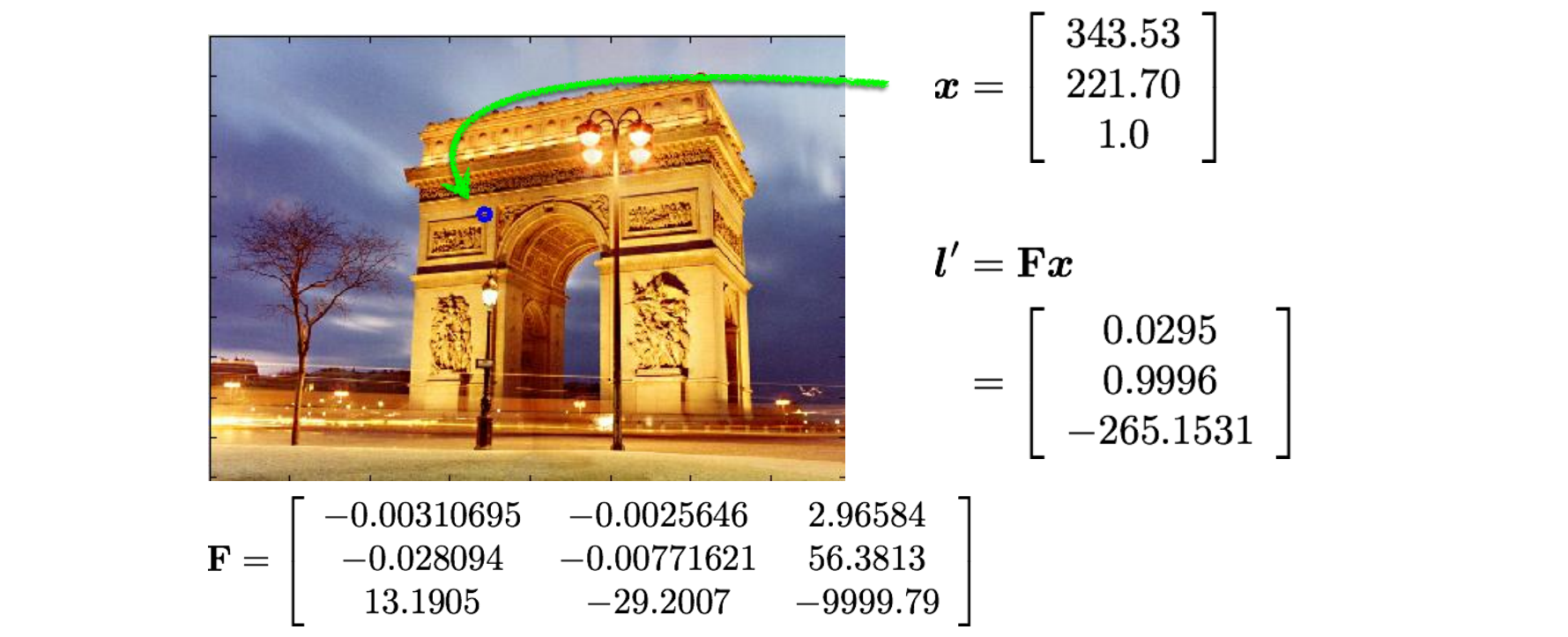
image.png

image.png

  • 另一张图上的点即在l’线上l匹配点

image.png

From Epipolar Geometry to Camera Calibration

  • 估计基本矩阵称为 “弱校准”(“weak calibration”)

  • 如果我们知道两台相机的内参矩阵，我们就可以估计基本矩阵：E = K′.TFK,可以通过F计算出E

  • 基本矩阵为我们提供了相机之间的相对旋转和平移，或它们的外部参数

  • 或者，如果内参矩阵已知（或者在实践中，如果内参函数有很好的初始猜测），则可以使用五点算法来估计相对相机姿态

One Application of the Essential Matrix

  • 基本矩阵 E 描述两个相机的相对运动

  • 给定一个估计的 E，我们可以得到相对旋转和平移，即外矩阵

  • 然后我们可以使用内联矩阵和外内联矩阵通过三角剖分(triangulation)计算 3D 位置

从基本矩阵中分解 R、t

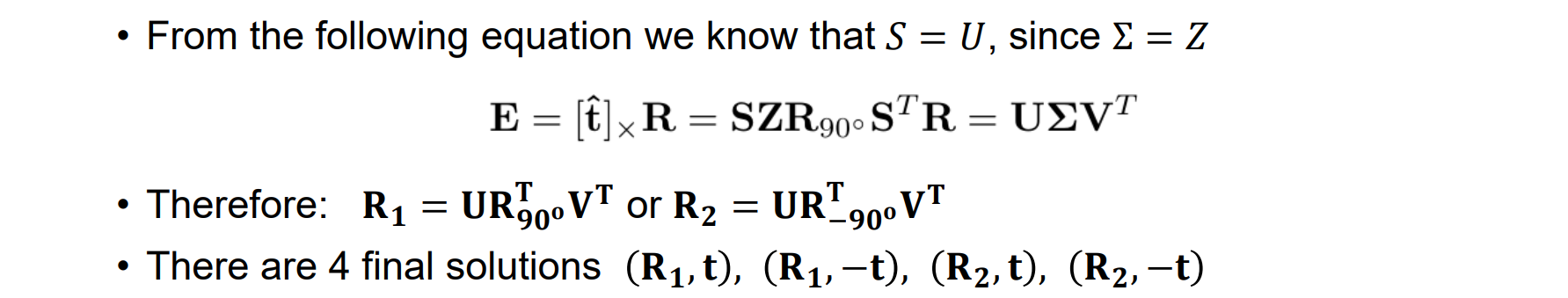
image.png

image.png

  • 通过检查正深度约束来确定最后一个:
    1. 要使 3D 点有效，它必须位于两个摄像头的前面
    2. 通过使用每种可能的解决方案对点进行三角测量(triangulating)并检查它们的深度，我们可以确定哪种配置是正确的