3D Vision

Single-view Ambiguity(单一视角的歧义性)

  • 3D Vision:从图片中重建三维结构

  • 关键问题：单一视角的歧义性。给定一个相机和一个图像，许多 3D 点可能会投影到同一个 2D 像素

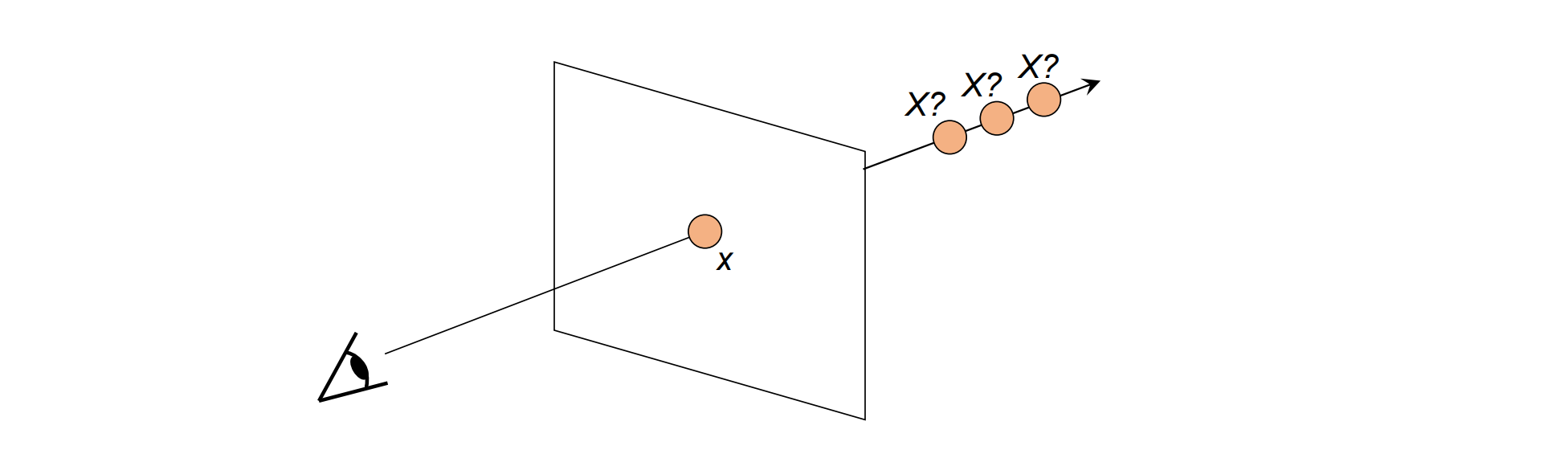
image.png

image.png

  • 单一视角的模糊性使得投影具有歧义性，产生投影错觉

Resolve Single-view Ambiguity

  • F1:从传感器中射出光（激光、结构光等）

image.png

  • F2:双目立体视觉：使用 2 个不同视图和对应关系的校准相机。拍两张照片，类似于双目视差进行校准

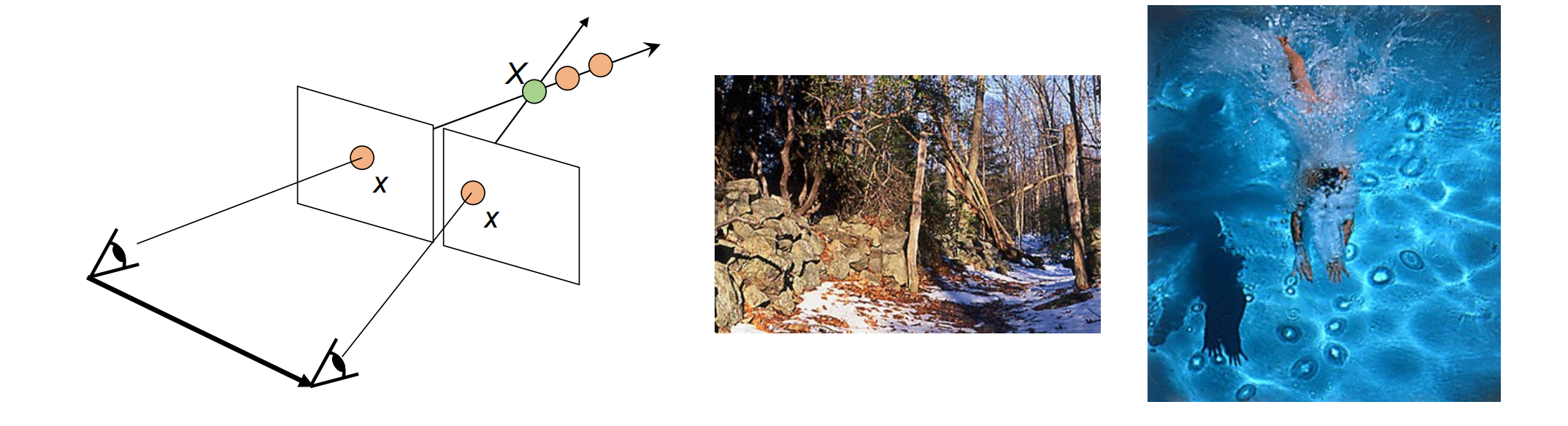
image.png

  • F3:多视图几何图形：移动相机并查找对应关系以求解 X,拍摄多张照片用SIFTfeature来求解

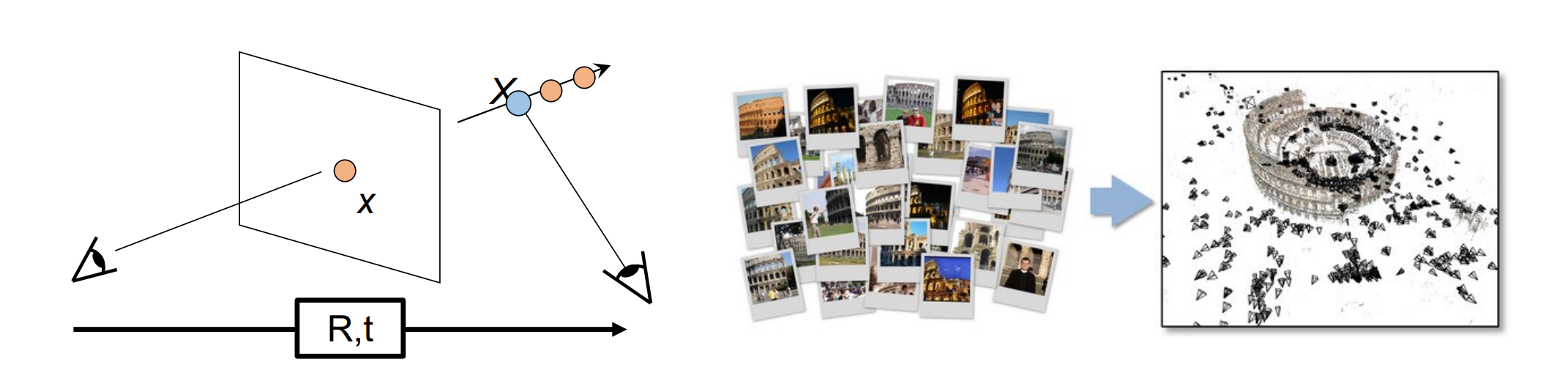
image.png

  • F4:Shape from Shading(三维明暗重建三维)：固定相机，并使用在不同阴影下拍摄的照片重建几何图形

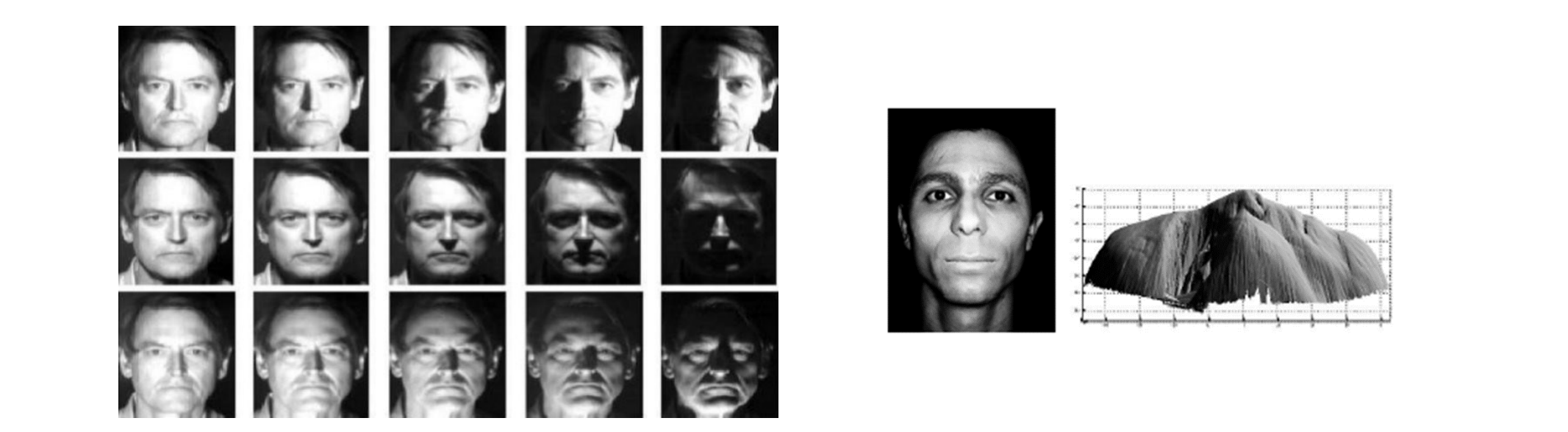
image.png

  • F5:从数据中学习：训练神经网络以预测 3D 信息。用神经网络估计深度解释歧义性

image.png

Camera Calibration(相机校准)

  • 核心：找匹配点

Review: Camera Parameters

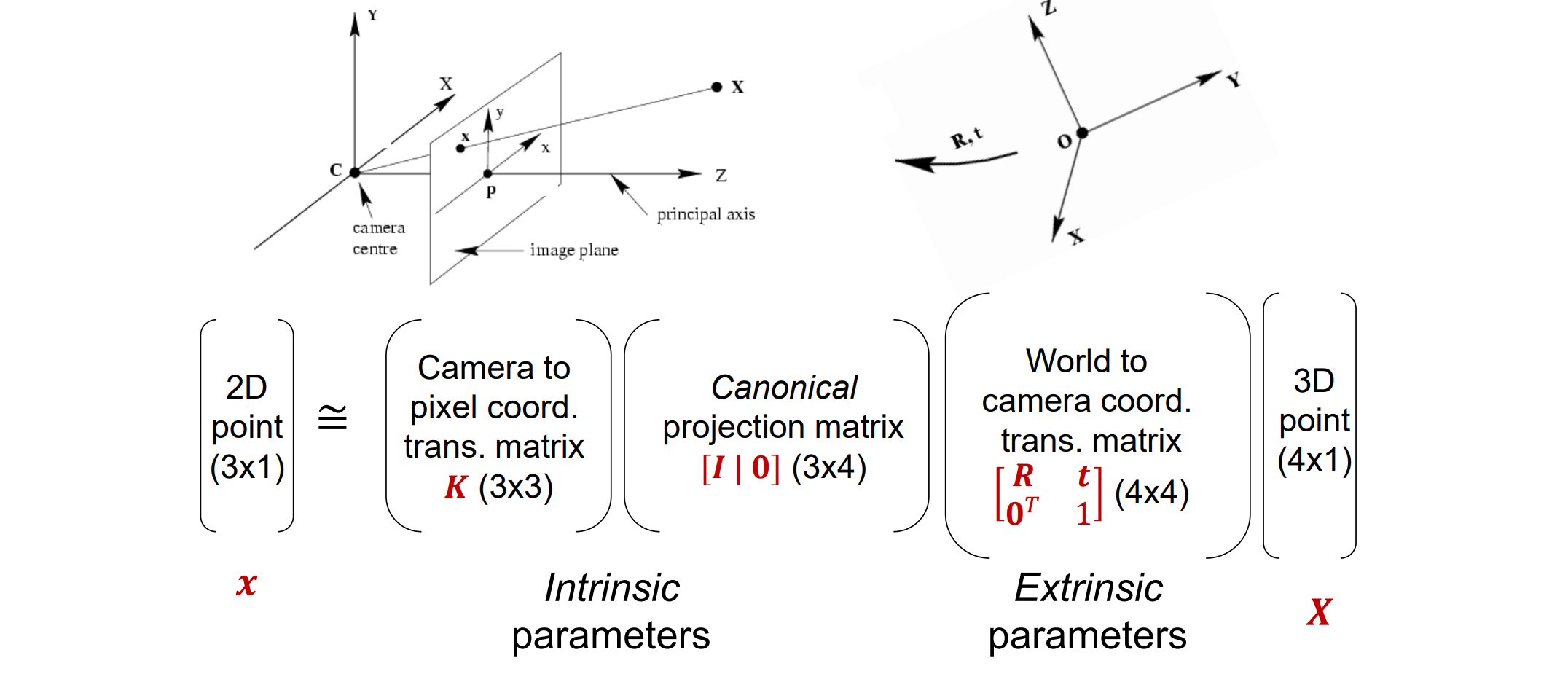
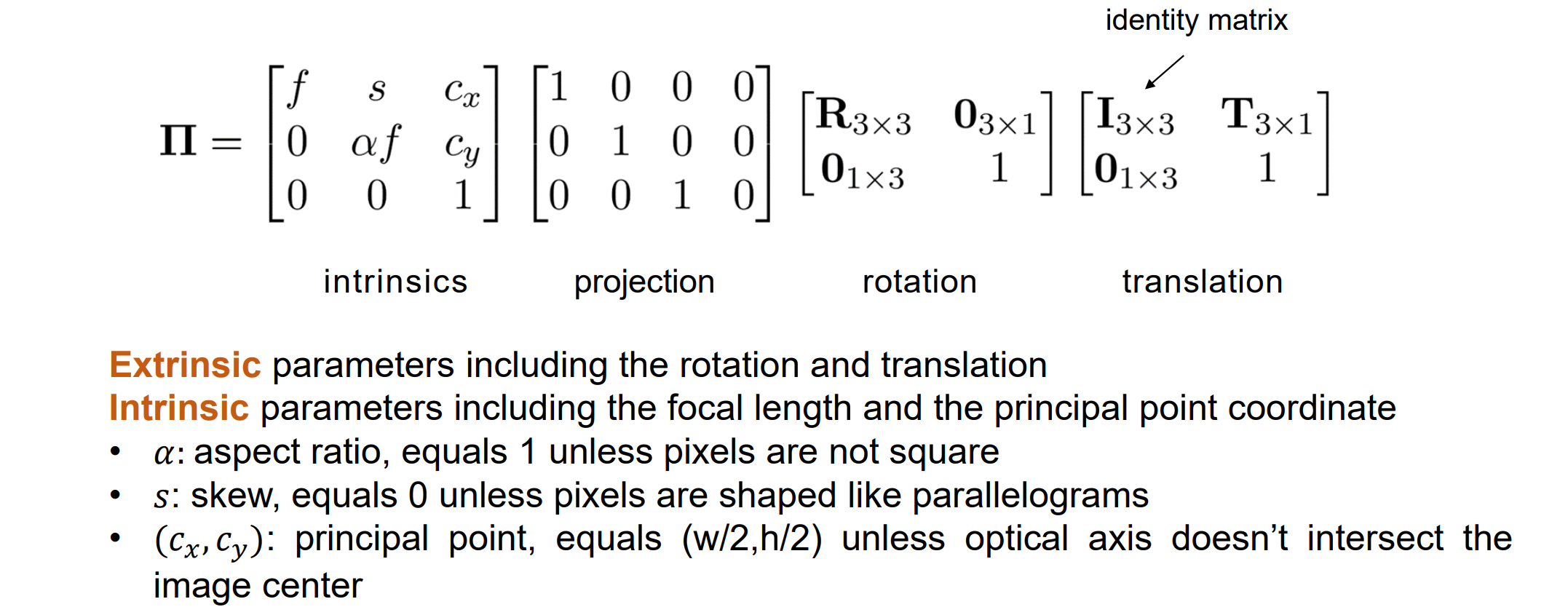
image.png

image.png

Camera calibration

  • 任务描述：Given 𝑛 points with known 3D coordinates 𝑿𝑖 and known image projections 𝒙𝑖, estimate the camera parameters。已知n个坐标和对应的投影坐标，需要估计相机的参数

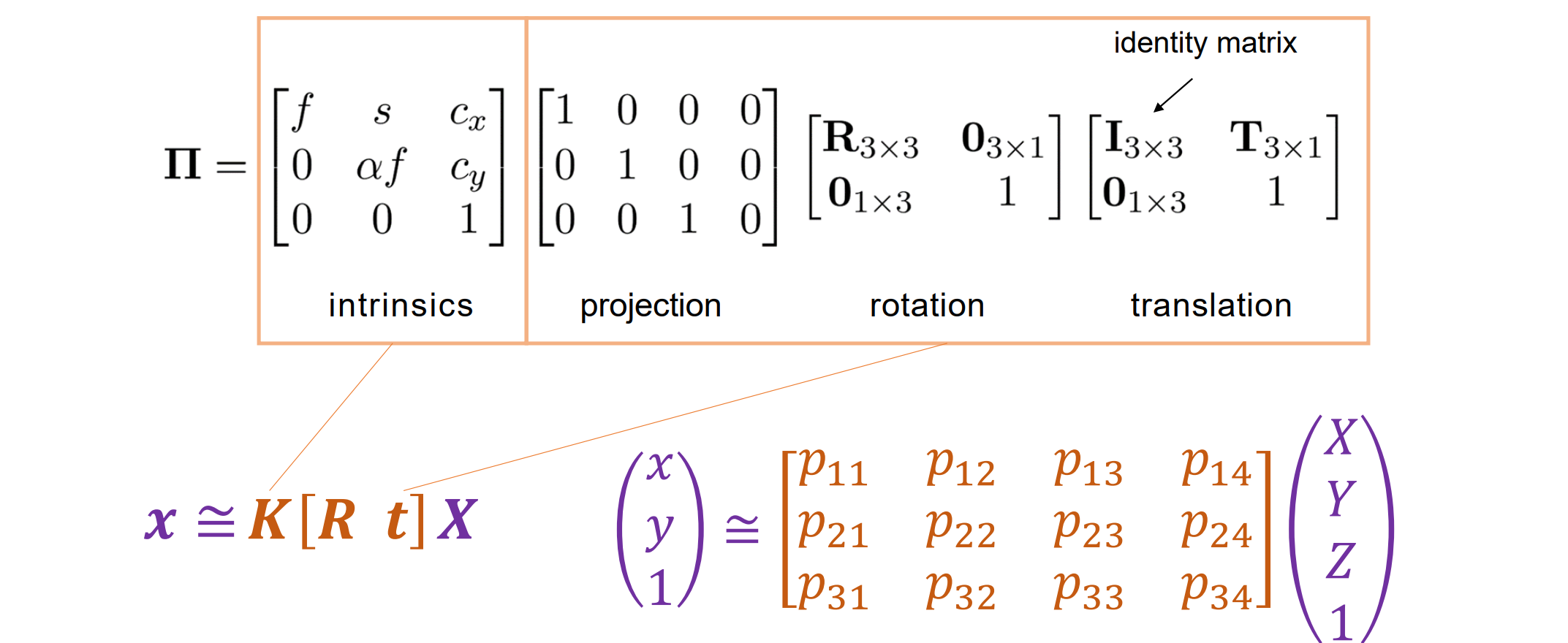
image.png

  • ≌说明不考虑缩放，是其次坐标。P矩阵是参数矩阵，是未知的要进行校准的。先求P矩阵，再进行矩阵分解

Camera calibration: Linear method

  • Pairs of correspondence points (𝑥𝑖, 𝑦𝑖) ↔ (𝑋𝑖, 𝑌𝑖, 𝑍i),有：

image.png

  • 一共有11个自由度，至少需要6个not colinear的点。在实际应用中，我们可以在对应中找到更多的点对。通过考虑 |p|²=1 来最小化以下能量函数：

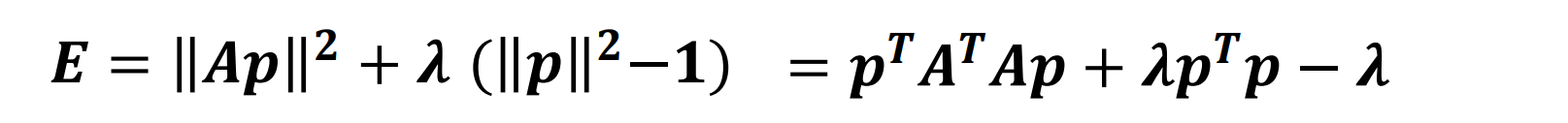
image.png

  • E 是二次的，我们取它的一阶导数，让它为零：结果为A.TA的特征值最小的特征向量

image.png

Camera Calibration: Linear vs. nonlinear(从P中如何求得K,R,T)

  • 线性校准很容易制定和解决，但它并不能直接告诉我们相机参数

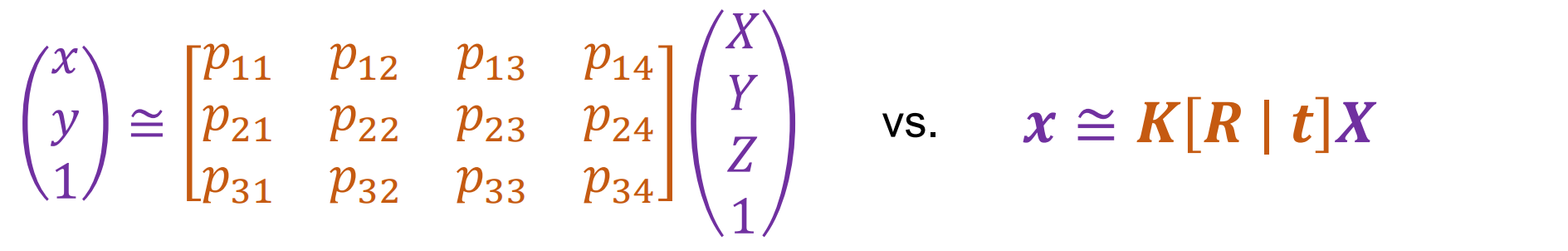
image.png

  • 观察到K是上三角矩阵，R是正交矩阵，因此可以通过RQ分解来得到K,R,T的值

image.png

  • RQ分解：QR 分解是 A 列的 Gram-Schmidt 正交化，从第一列开始。RQ 分解是 A 行的 Gram-Schmidt 正交化，从最后一行开始

  • 矩阵𝑃 = K [𝑹 | 𝒕] 的形状是 3 × 4 的。对最左侧的 3x3 矩阵进行 QR 分解，得到 K、R 。然后用 P 和 K 计算 t。求得K ^ (-1) 和P的最后一列从而得到t

  • 在实践中，非线性方法是首选：

    1. 将目标函数写下实测的 2D 点与估计的 3D 点投影之间的平方距离之和：
      image.png
    2. 可以包括径向变形和约束或其他约束
    3. 使用非线性优化包将误差降至最低
    4. 使用线性方法的输出初始化解决方案（使用 RQ 分解从 P 获得 K 和 R）

Triangulation(三角测量)

  • 任务描述：给定一个 3D 点在两个或多个图像中的投影（使用已知的相机矩阵），找到该点的坐标。通过求解对应点来进行三维重建

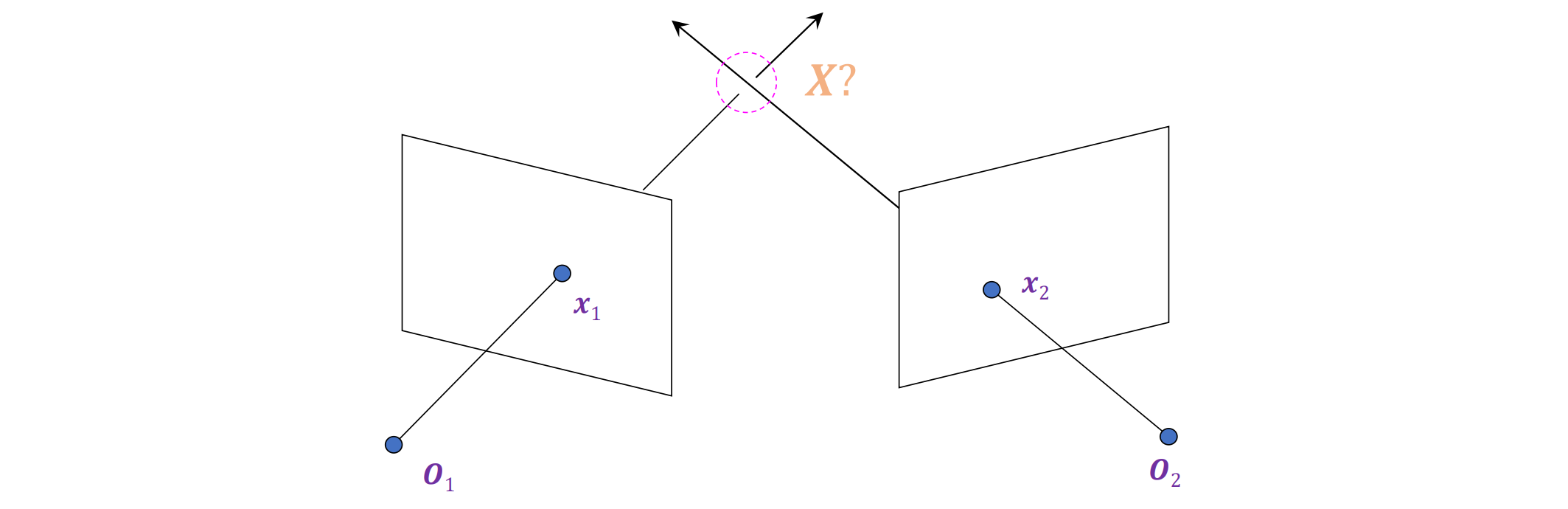
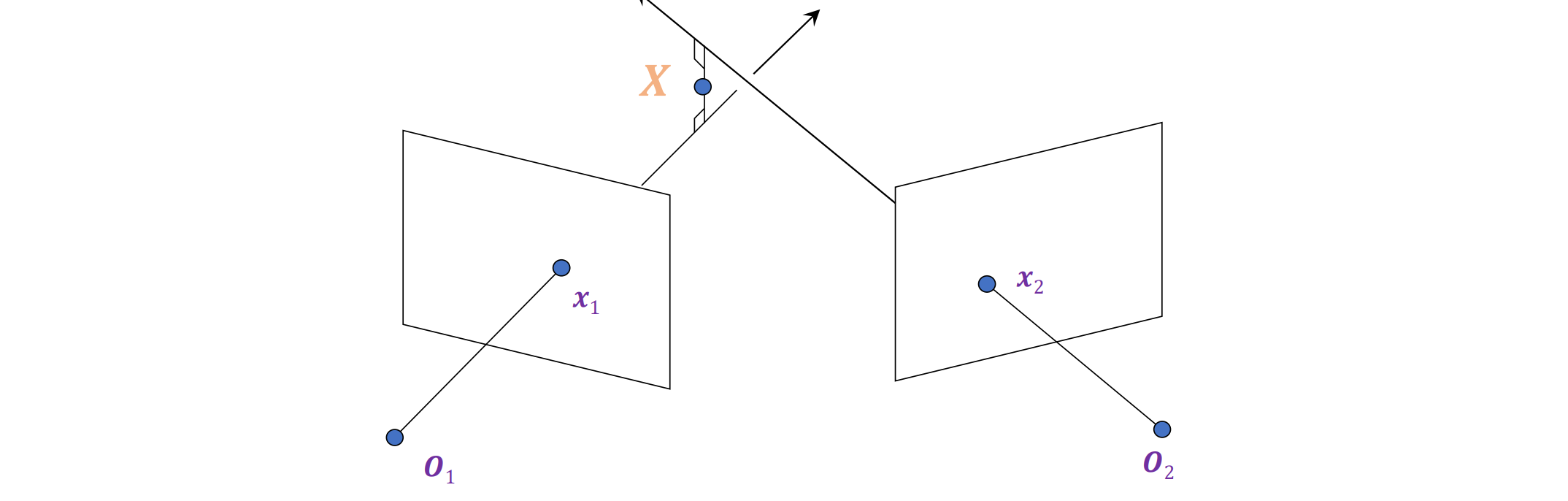
image.png

  • 理想状态下，对应的 x1 和 x2 的两条视觉光线相交，但由于噪声和数值误差，它们并不完全相交

  • Triangulation #1: Geometric Approach:找到连接两条观察光线的最短线段，并设 X 为该线段的中点

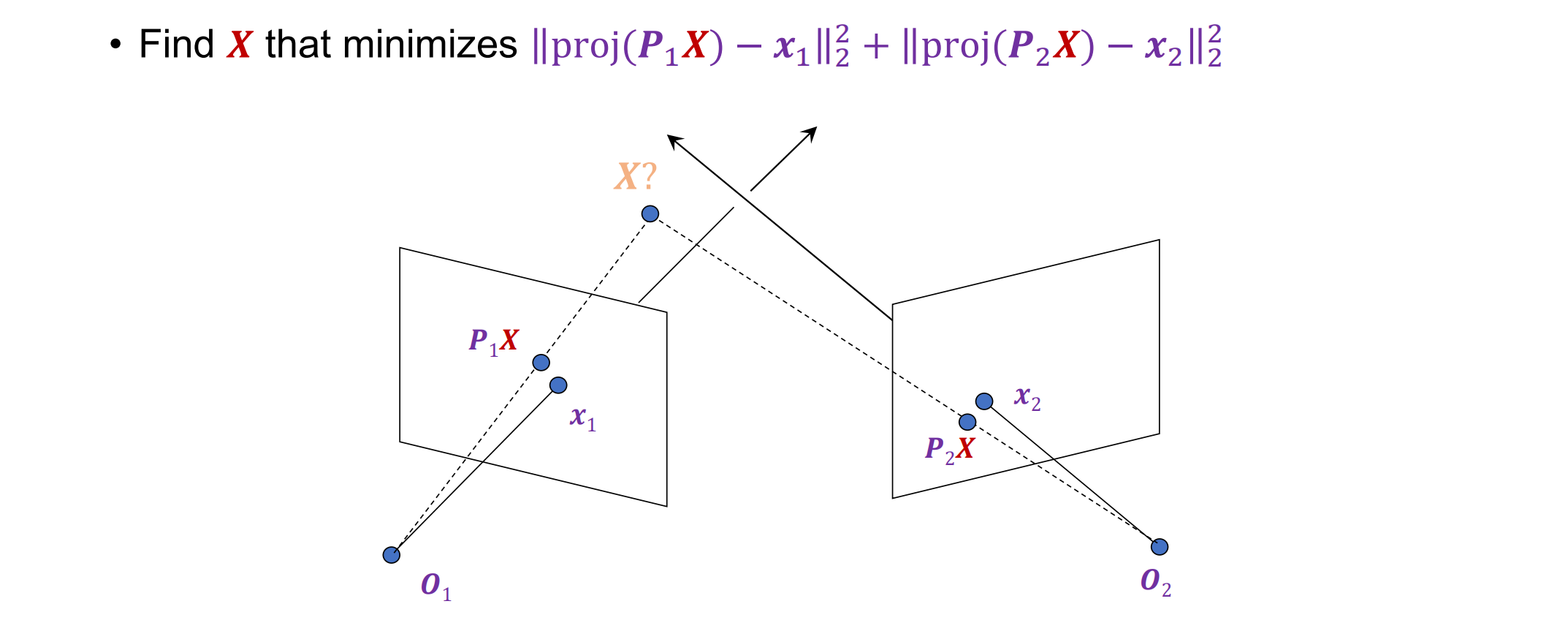
image.png

  • Triangulation #2: Nonlinear Approach:非线性求解找到实际投影点与x1,x2距离的差的平方之和的最小值

image.png

  • Triangulation #3: Linear Optimization:线性优化问题，未知量为X，由于等比例缩放相等，因此可以写成叉乘形式。一个矩阵方程可以得到两个小方程。两个相机可以得到四个方程，而X有3个自由度，因此可以通过最小二乘法求解：

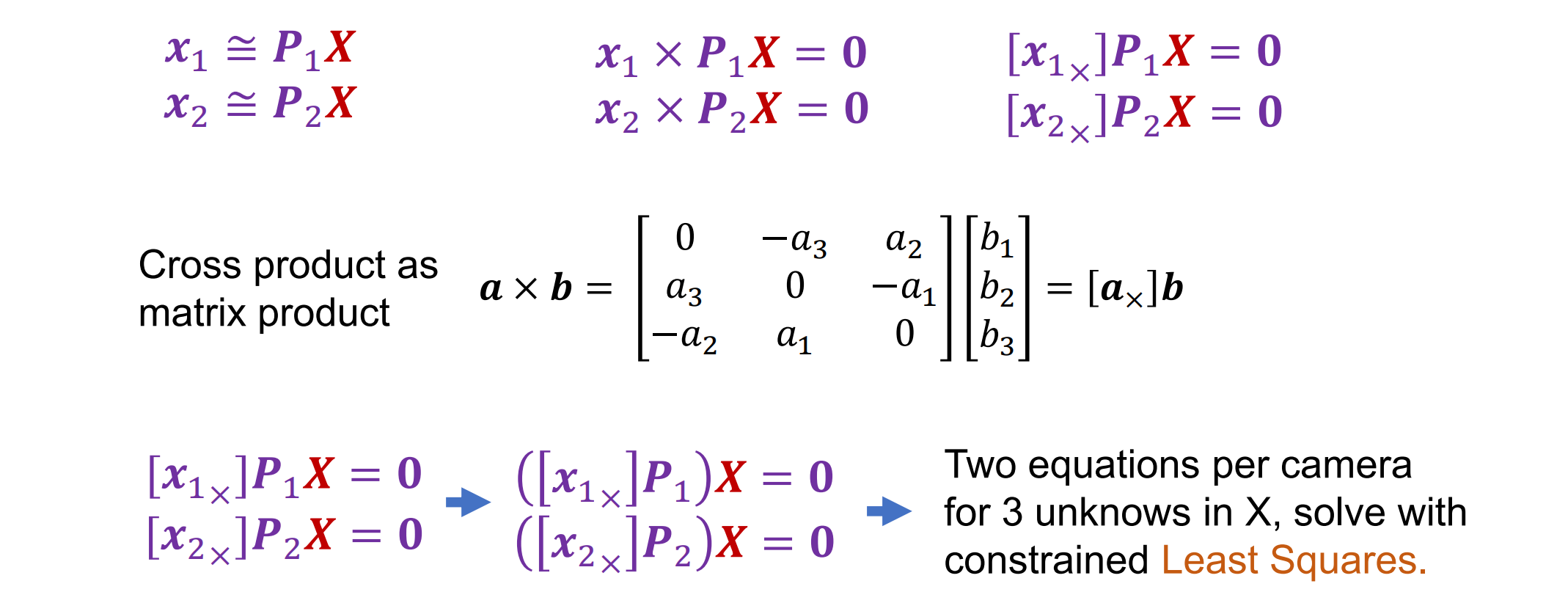
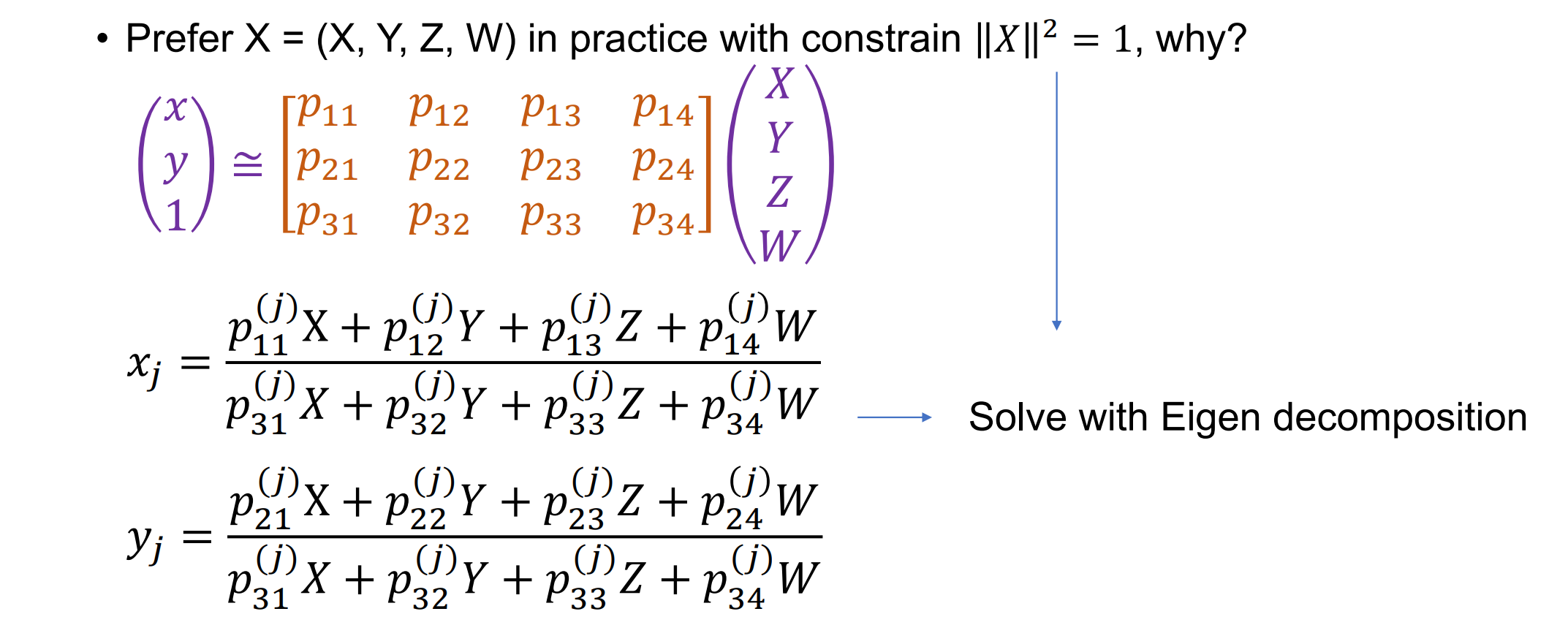
image.png

image.png

  • 其中j是相机号，用特征值求解来解决问题

Calibration with Vanishing Points

  • 如果不知道3D点的世界坐标，在特殊情况下，我们可以使用消失点

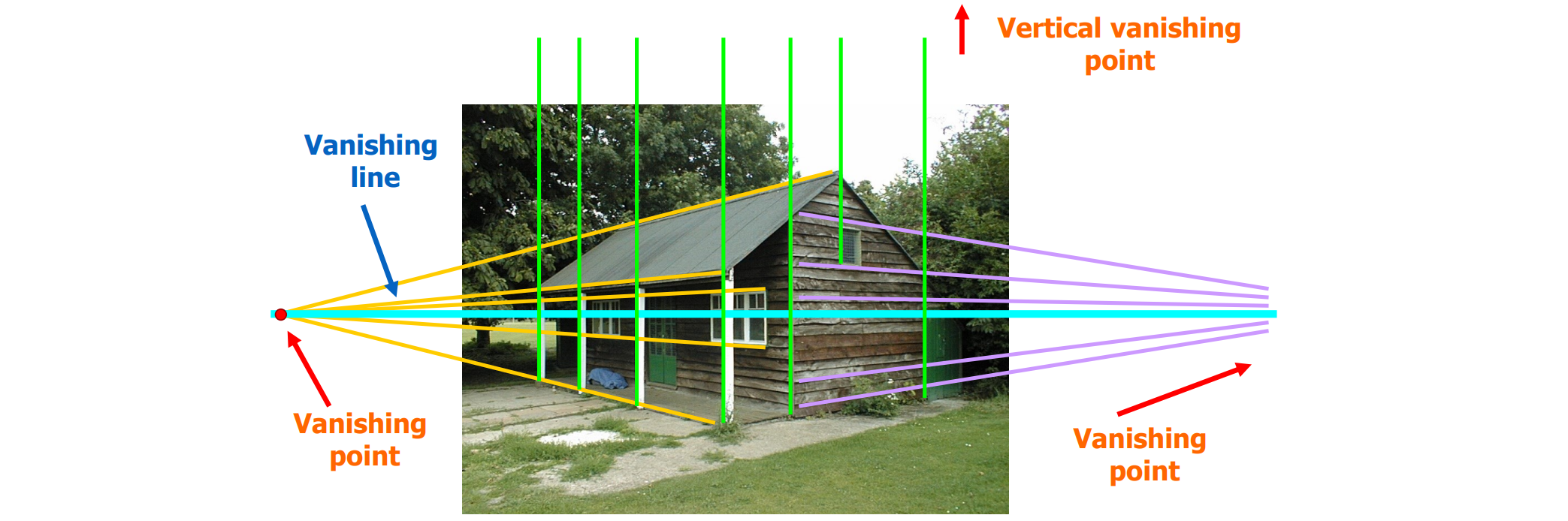
image.png

  • 可以推出相机平行于绿色的Vanishing line

Review: Vanishing Points

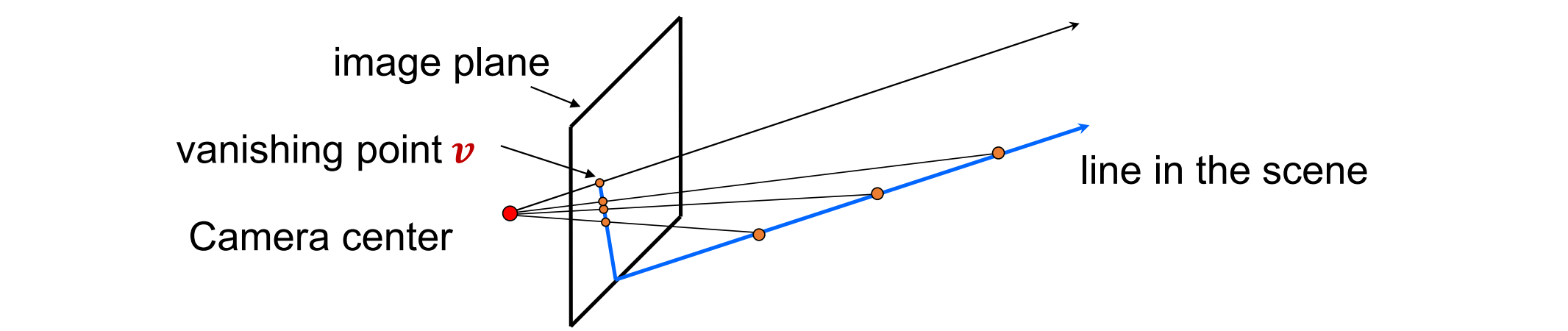
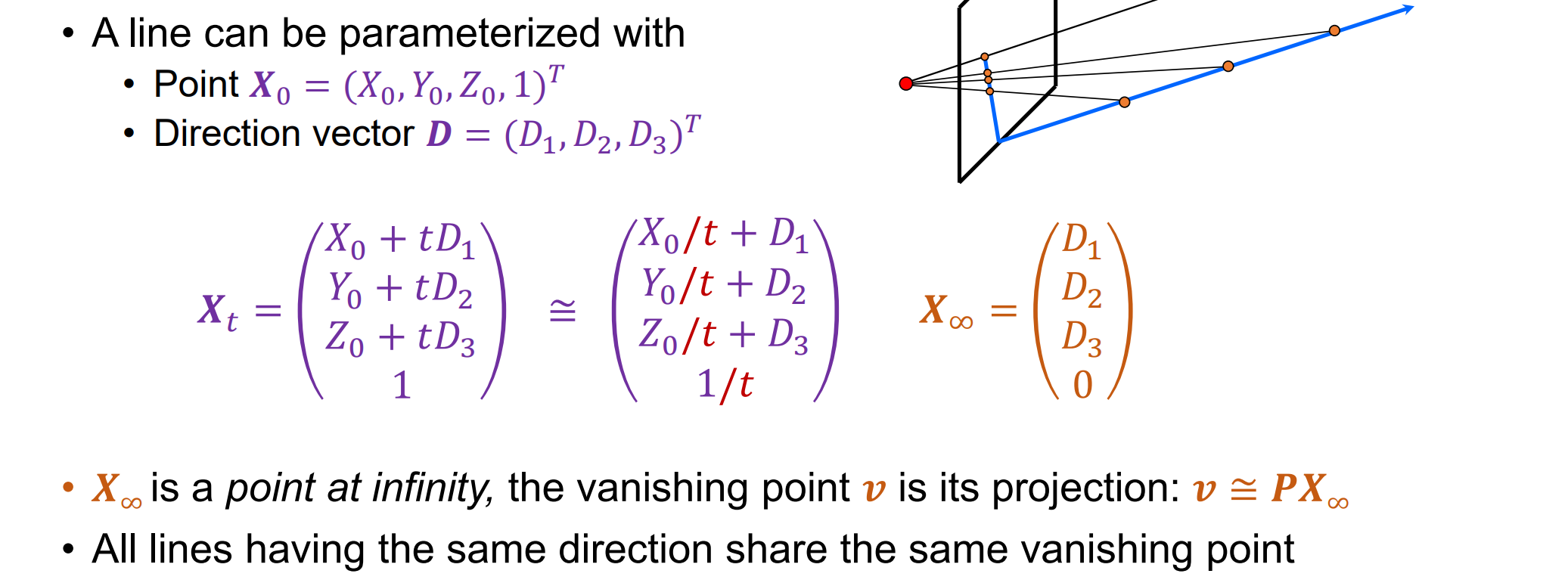
image.png

image.png

Calibration from vanishing points

  • 考虑一个具有三个正交消失方向的场景。v1，v2是有限消失点，v3 是无限消失点。将世界坐标系与这些方向对齐。

image.png

  • 可以通过找直角来得到v1，v2。v3是无穷远点，相机平行于Vanishing line3，可以通过v1,v2,v3求得相机参数：

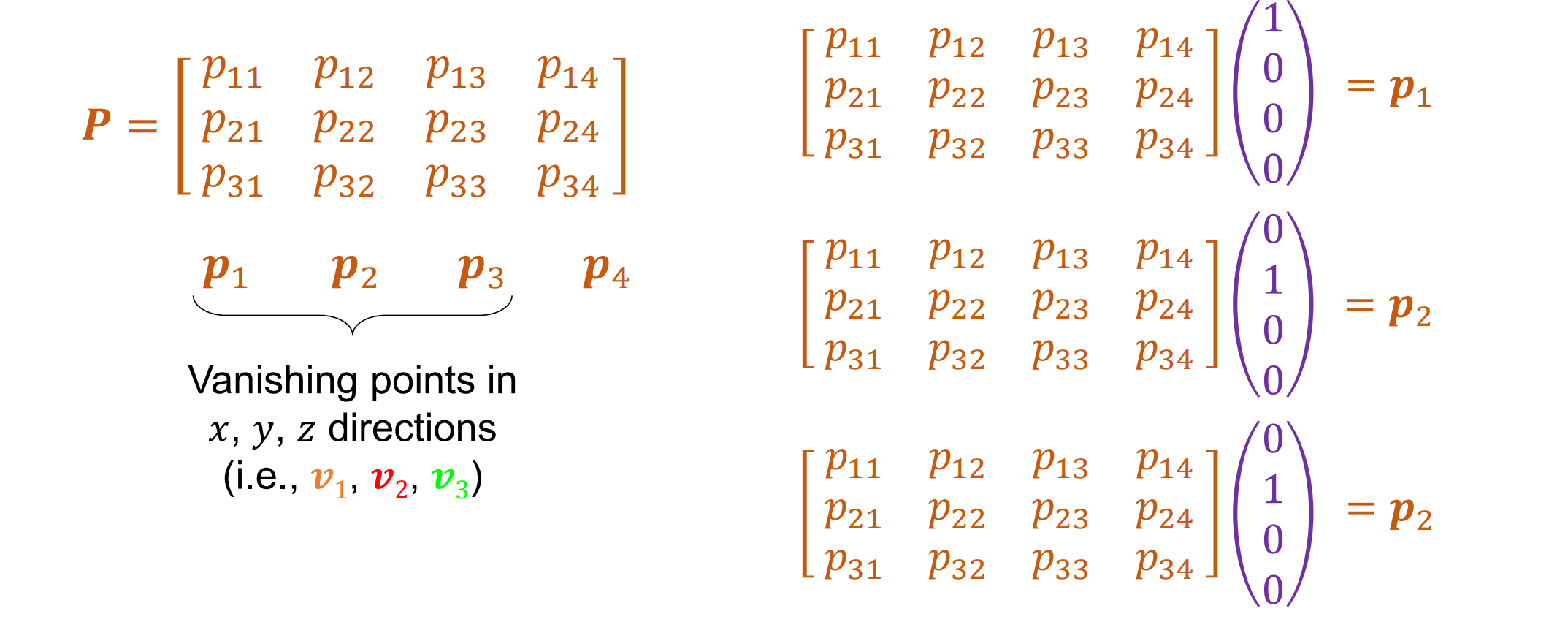
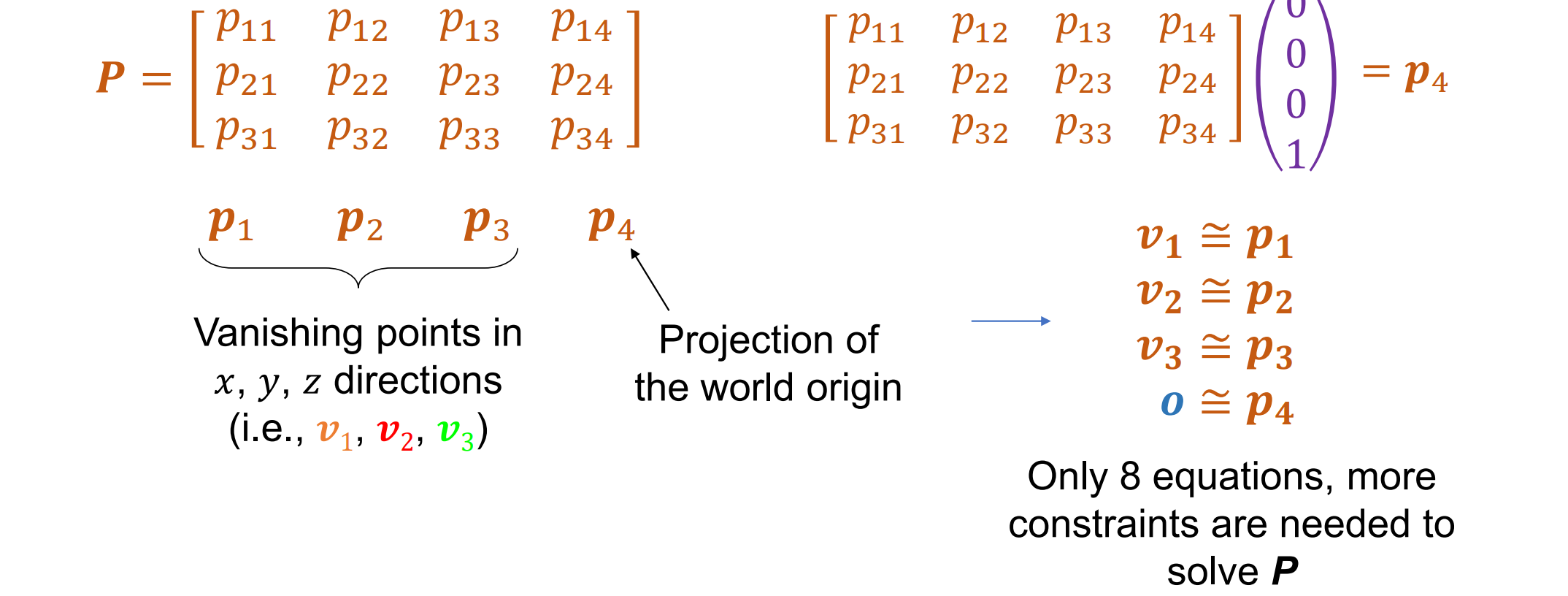
image.png

image.png

  • P矩阵的前三列是三个Vanishing point的坐标，而第四列是原点投影。四个方程可以得到8个小方程，但是P矩阵有12个自由度，因此仍需要约束：v1,v2的直角关系

  • 我们将世界坐标系与场景中的三个正交消失方向对齐：

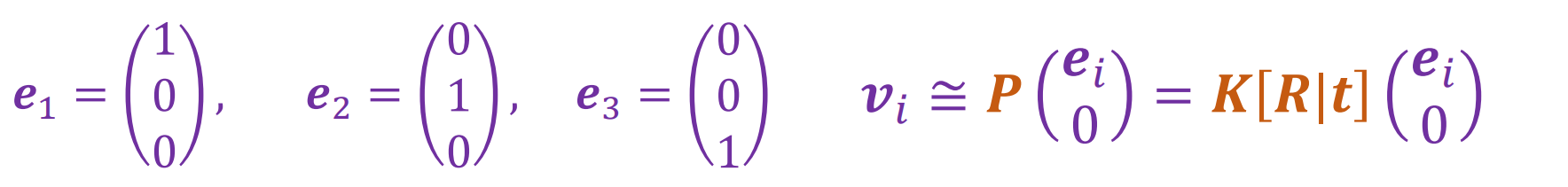
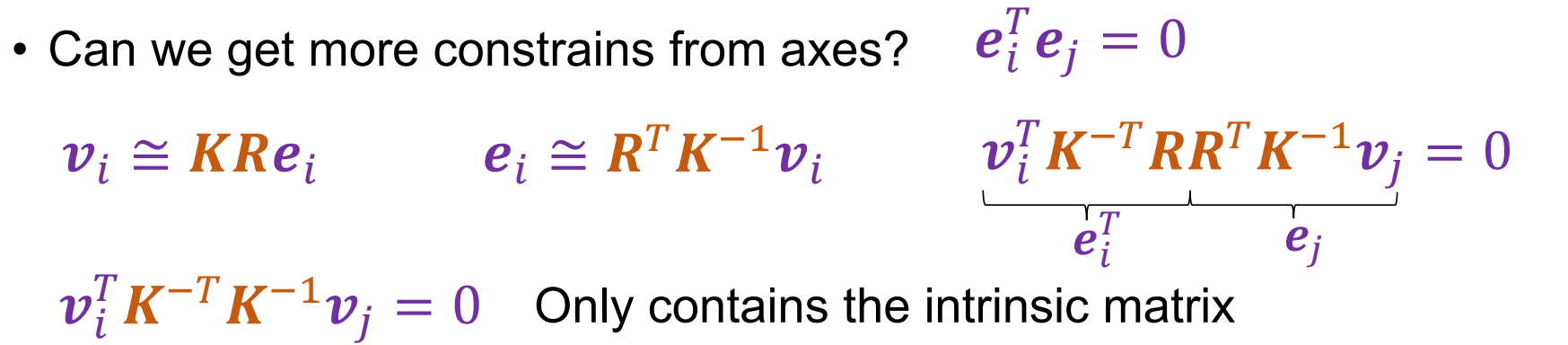
image.png

image.png

  • 可以看到一对Vanishing point可以得到一个约束，因此可以得到3个约束，而内参矩阵K正好有3个自由度

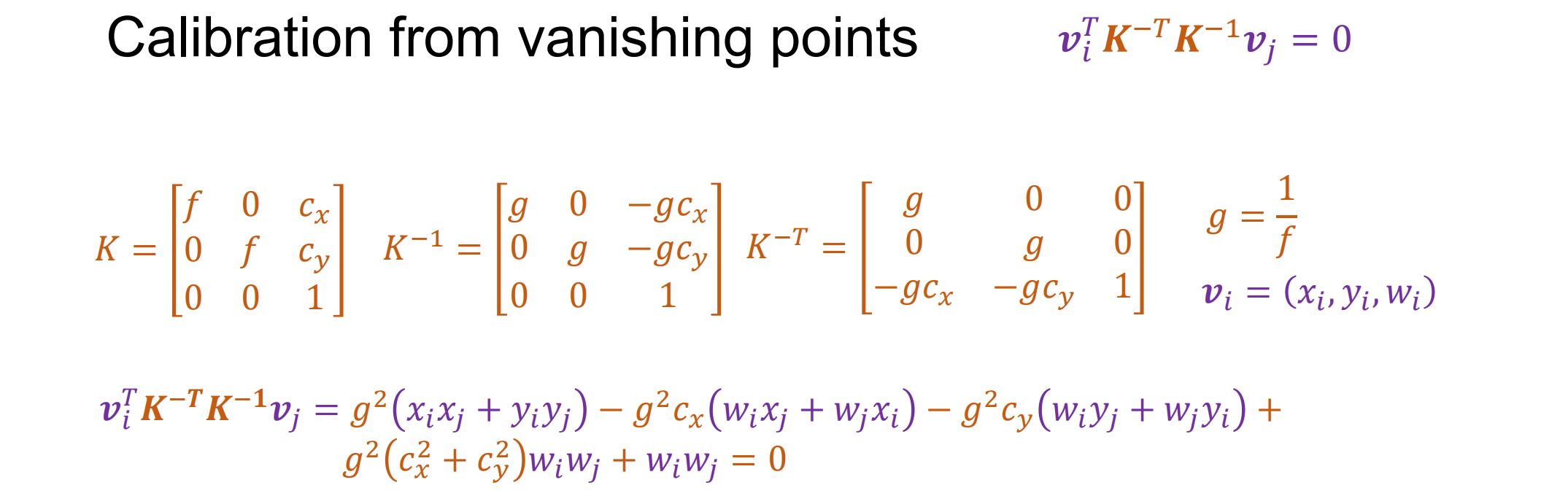
image.png

  • 一些复杂情况：

    1. 约束是非线性的，但并不难解决
    2. 至少需要两个有限消失点来求解 f 和 cx,cy否则至少有一个wiwj=0从而少一个等式

  • Calibration from Vanishing Points：

    1. 使用三个正交消失点求解固有参数（焦距、主点）
    2. 一旦知道校准矩阵，就直接从消失点获取外部参数（旋转）(如下所示)
    3. 优点：无需校准图表，2D-3D 对应关系，可以完全自动化
    4. 缺点：仅适用于某些类型的场景，准确定位消失点很棘手，并且至少需要两个有限的消失点

Rotation from vanishing points

image.png

Summary

image.png