Edge Detection

  • Edge Detection: Identify sudden changes (discontinuities) in an image

  • 可以用导数来描述”sudden changes”

Partial Derivative

  • 导数：函数 f（x） 沿某个方向在某一点上变化的速率；梯度：所有偏导数堆叠在一起而形成

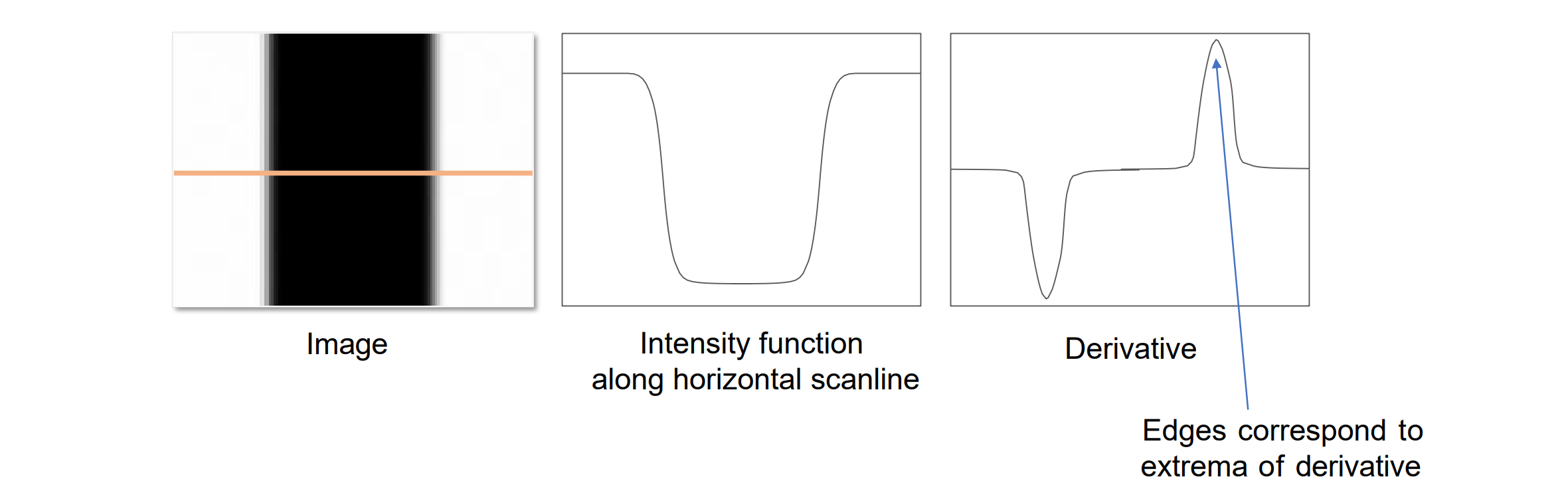
image.png

  • 图像的偏导数(图像可以描述为2D function f(x,y)):

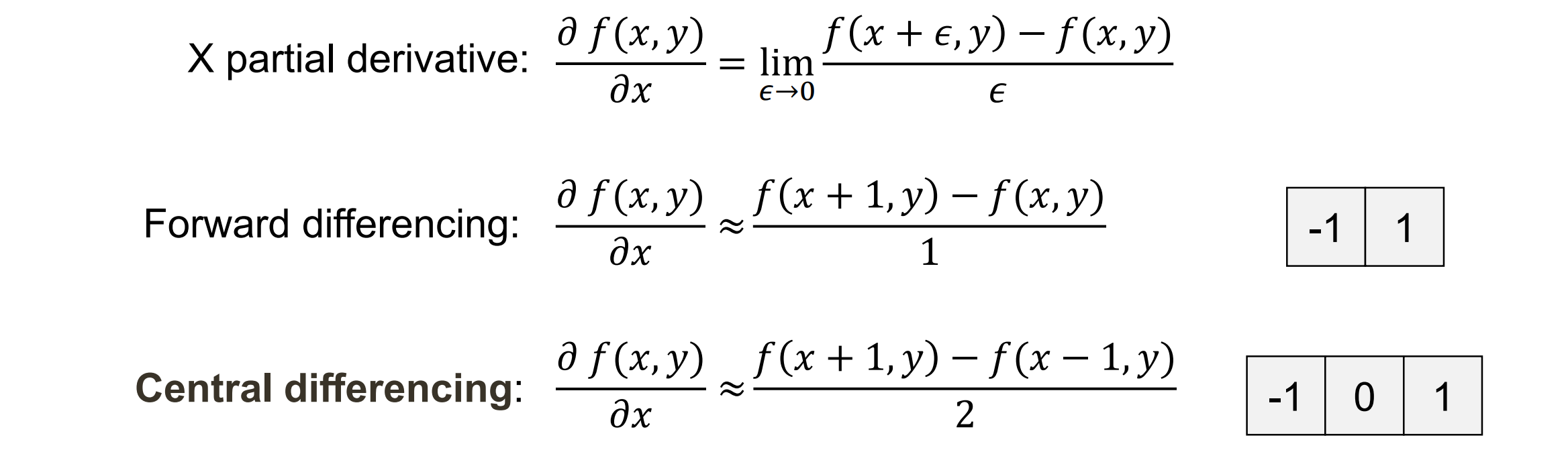
image.png

  • 图像的偏导数可以用图像的滤波来计算：水平竖直方向分别用滤波卷积计算

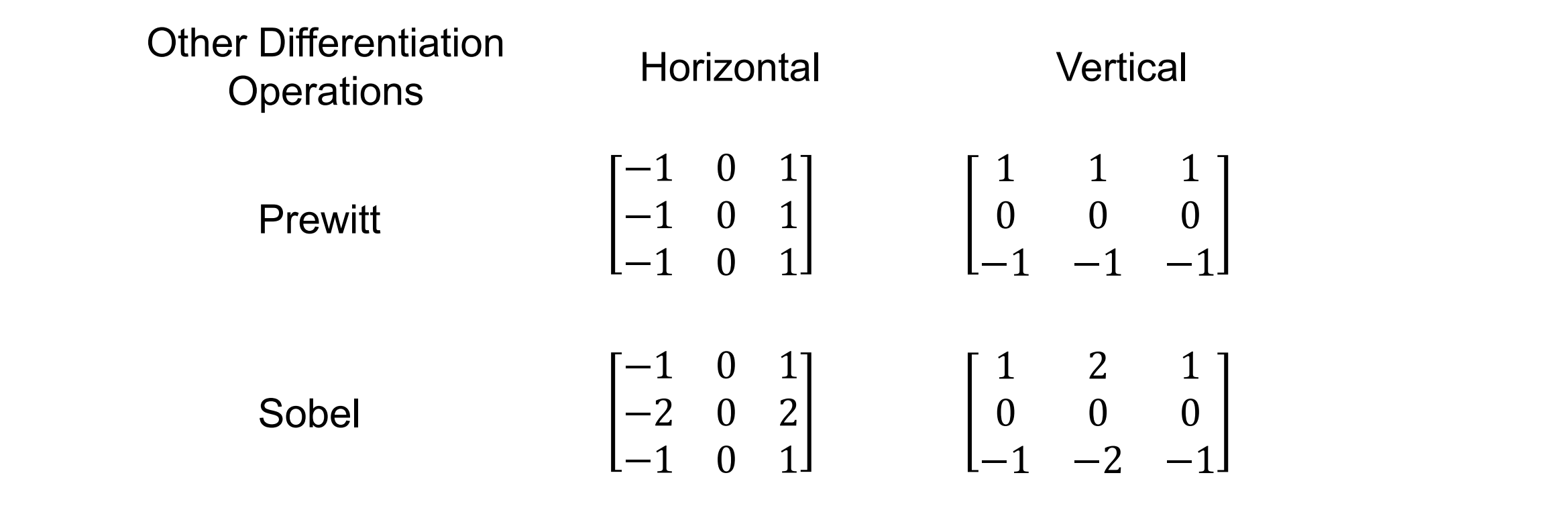
image.png

  • 每一个方向先前向差分再归一化，水平、竖直方向拼起来形成梯度

  • Noise Severely Affects Derivatives of an Image：求梯度的时候噪音的梯度被放大，主导图像的梯度

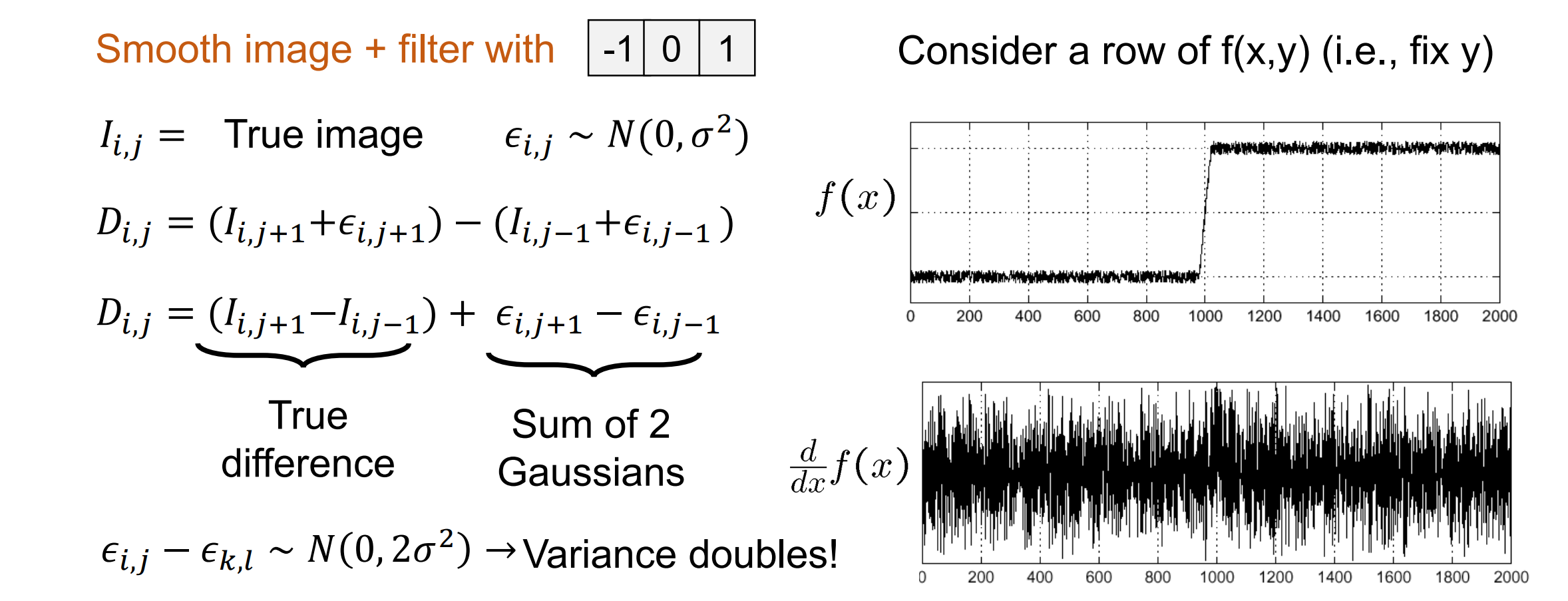
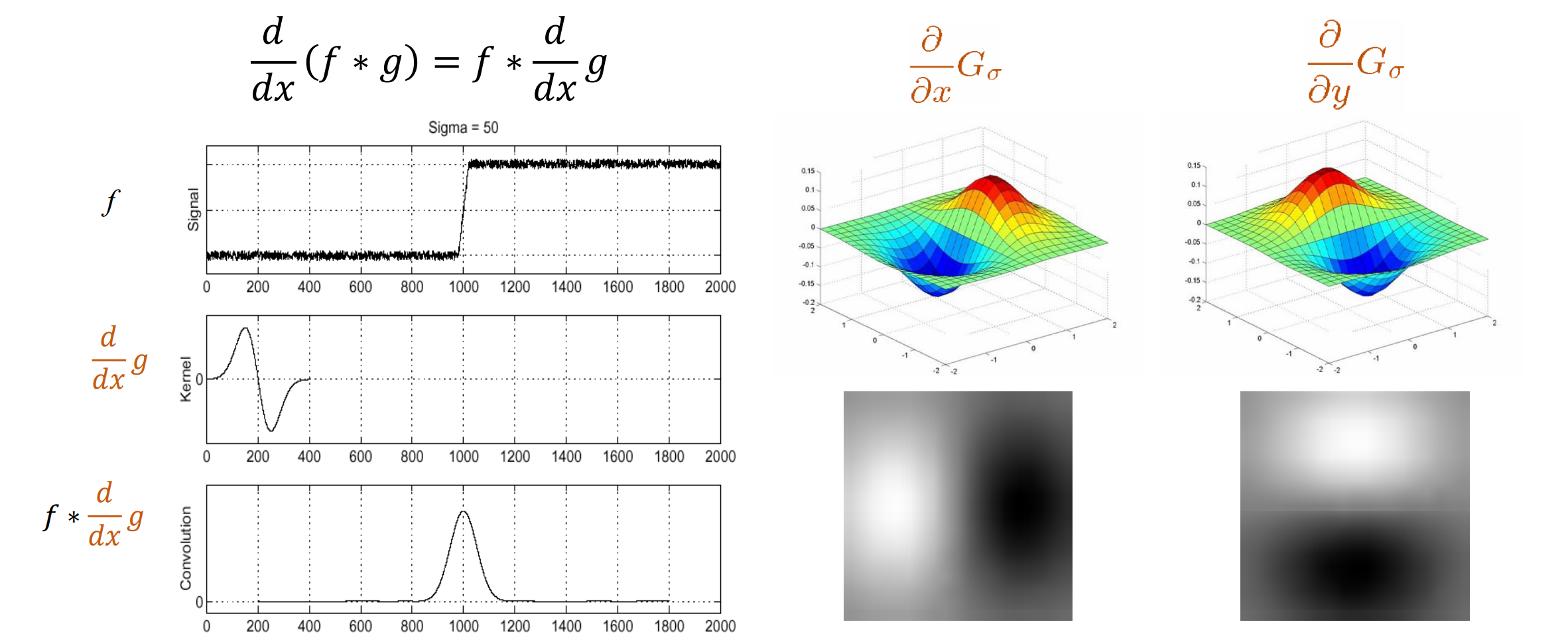
image.png

  • 解决办法：先对图像做平滑处理，可以先对图像用高斯滤波，然后再进行边缘检测求梯度。经过数学推导改变偏导顺序可以把这个过程变为：

    1. 先对高斯求偏导
    2. 再对函数进行滤波求梯度
    3. 最后归一化
      image.png

  • The gradient direction is given by:

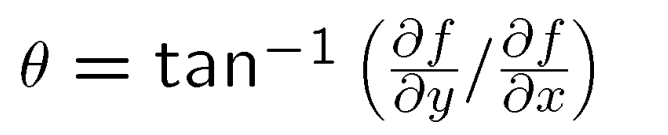
image.png

  • The edge strength is given by the gradient magnitude(梯度幅度):

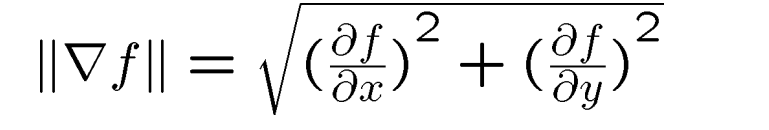
image.png

Canny Edge Detector

  • Canny Edge Detector的流程：
    1. 预处理: Grayscale conversion + Gaussion blur
    2. 使用中心差分来计算梯度图像（而不是第一次前向差分），这样更准确。
      kernelX = {1,0,-1,2,0,-2,1,0,-1}
      KernelY = {1,2,1,0,0,0,-1,-2,-1}
    3. 计算梯度幅度，是连续变化，需要加阈值
      image.png
    4. NMS非极大值抑制：消除误判导致的边界很粗现象，利用NMS使得Edge变得更细。遍历所有像素，仅保留edge detection中的最大值
    5. Double threshold(双阈值)：
      1. 高于高阈值，则置为edge(1)
      2. 低于低阈值，则置为非edge(0)
      3. 处于低阈值~高阈值之间的(weak edges)进入下一阶段的检测
        image.png
    6. Edge Tracking by Hysteresis(滞后现象)：
      1. weak edges如果能连接到此前置为1的edge则置为1
      2. 否则置为0

image.png

Corners(角点检测)

  • 初步定义角点：两条或多条边的交点

Harris Corner Detector

  • Key idea: characterize corners by measuring the intensity change when shifting a small local window，移动窗口查看变化

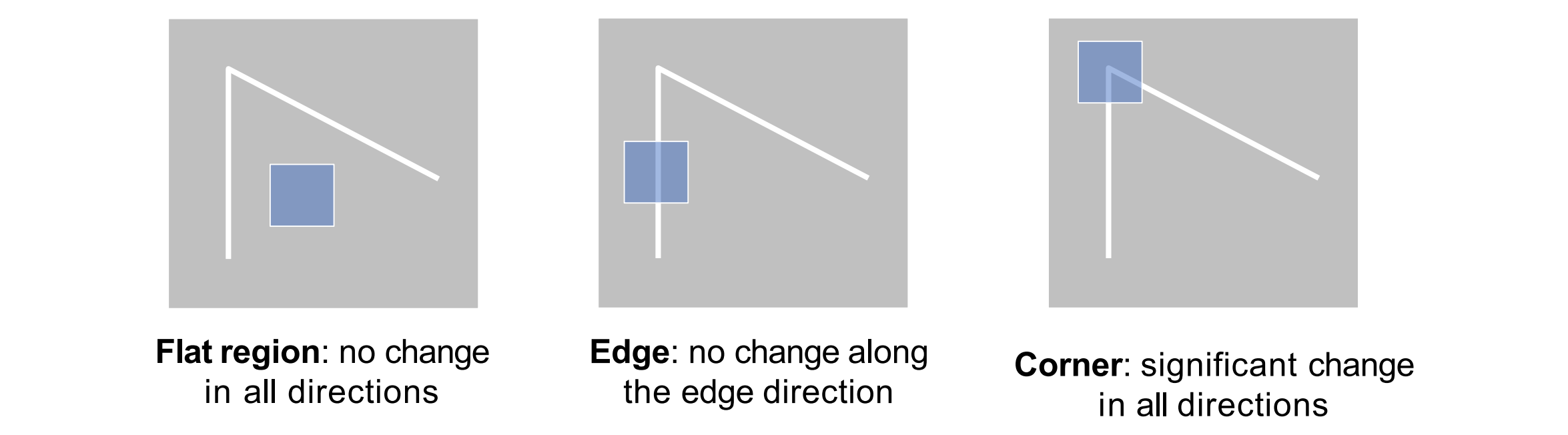
image.png

  • 移动窗口 W by (u,v)(点的平移)

  • 移位前后每个像素的强度变化可以通过将平方差 （SSD） 相加来定义：其中，I(x,y)是像素的值，w(x,y)是像素的权重

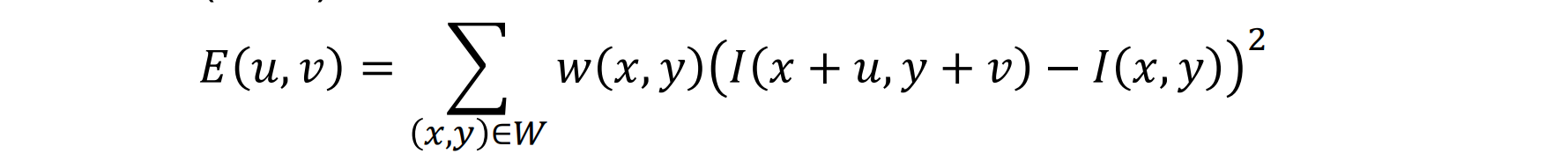
image.png

  • 缺点：循环遍历，精确计算所需时间很长

  • 泰勒展开：一种线性化函数的方法

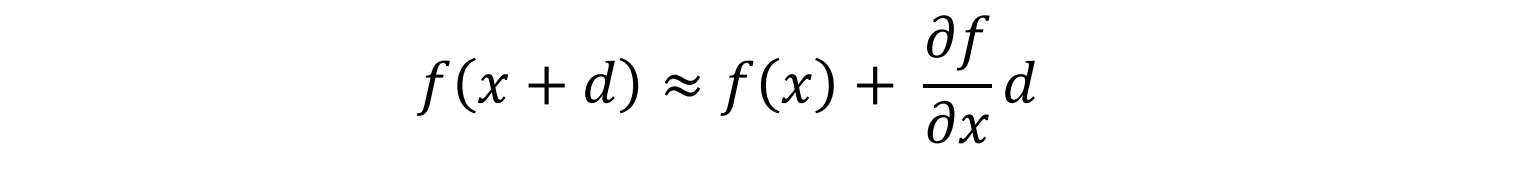
image.png

  • 将其用于图像中(Harris Corner Detector)可得：

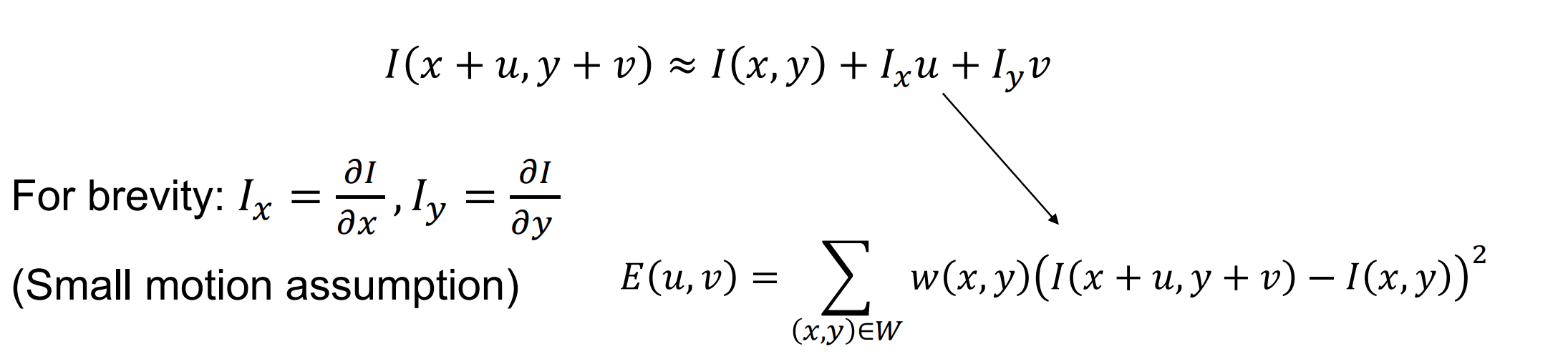
image.png

  • The Sum of Squared Differences with Taylor Series：形成二次型，M是半正定对称矩阵

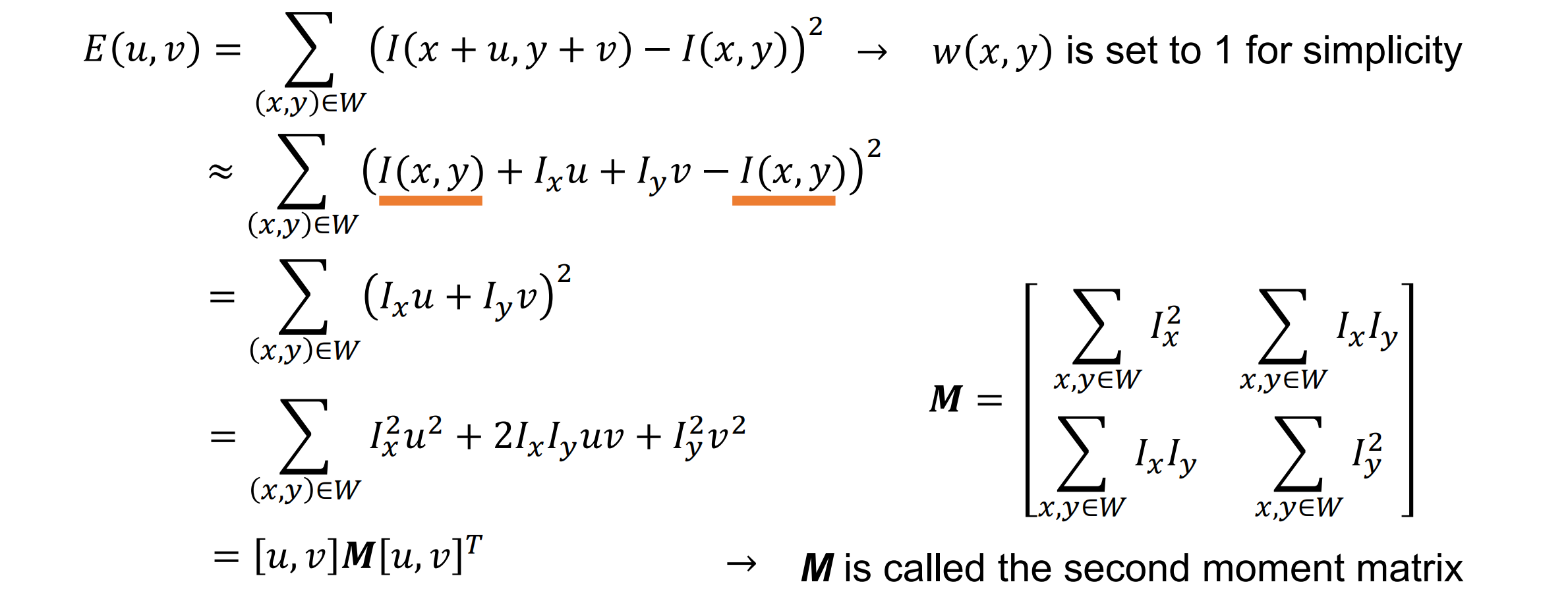
image.png

  • 对称矩阵M和向量[u,v]，假设：𝐸 [𝑢, 𝑣] = [𝑢, 𝑣] 𝑴 [𝑢, 𝑣].T。那么其等值线/切面，即是一个椭圆。𝐸 [𝑢, 𝑣]取不同值对应的椭圆面不同

  • 可以通过将 M 分解为旋转 + 缩放来查看这个椭圆的形状。其中𝜆1𝜆2是特征值

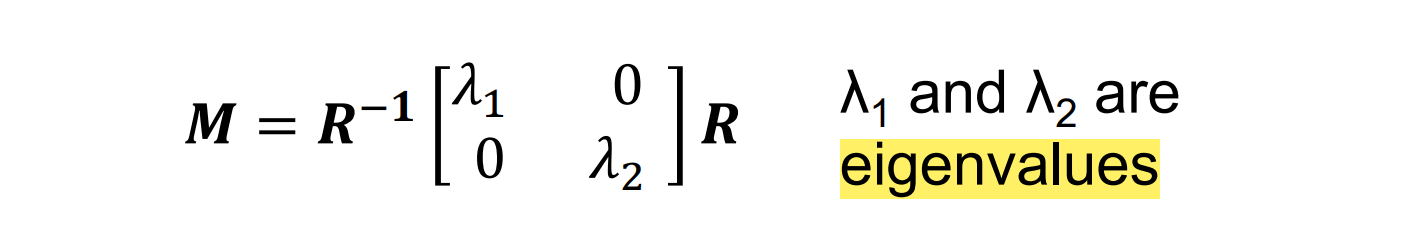
image.png

  • 特征值的解释：只有当𝜆1𝜆2都很大时，R才会很大，说明E在任何方向的变化都很大，此时为角点。否则𝜆1𝜆2任意一者小，R都会很小，不判定为角点

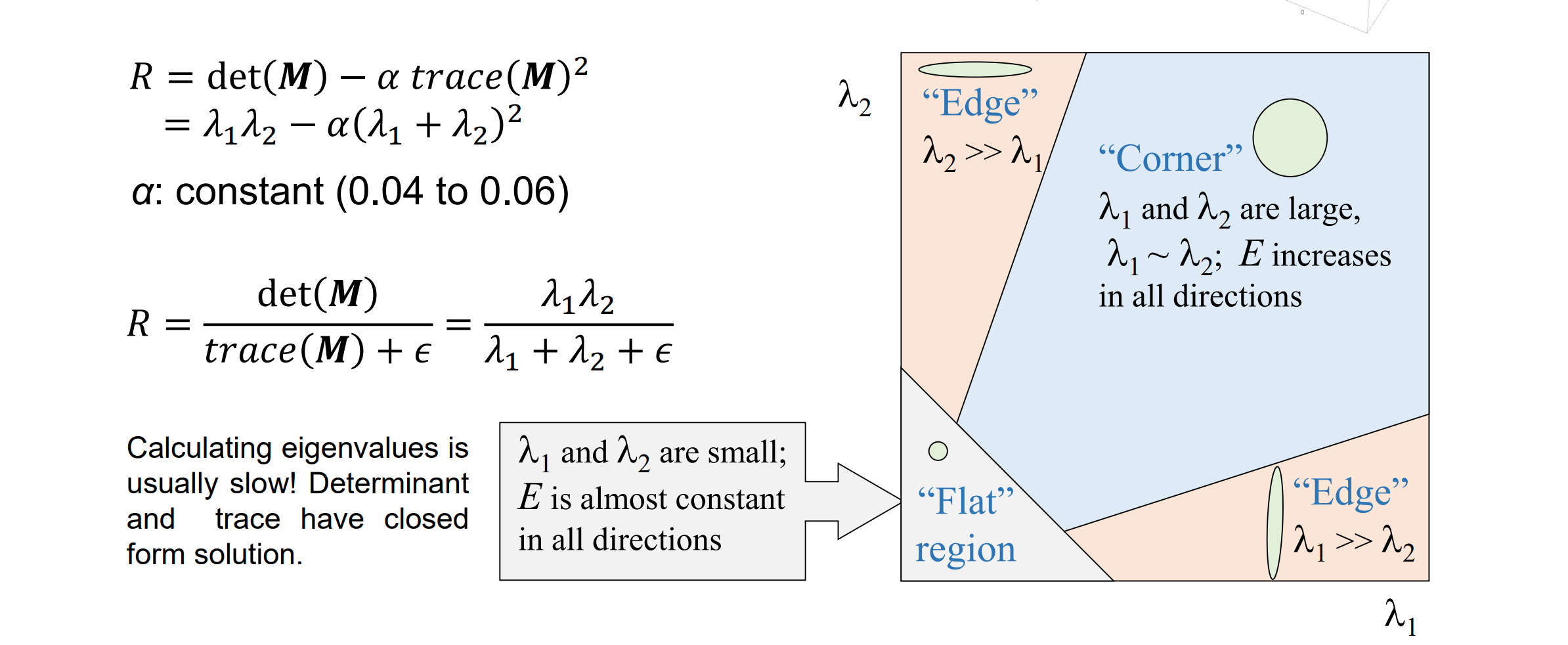
image.png

  • summary:
    1. 预处理：将输入图像转换为灰度并应用高斯滤波器
    2. 求梯度：应用 Sobel 算子查找 x 和 y 渐变值
    3. 求Harris 值：对于每个像素 p，考虑其周围一个 3×3 窗口，并计算第二个矩矩阵 M 和角强度函数 R
    4. 设置阈值 R 和应用非最大值抑制NMS

Properties of Corners(角点的性质)

  • 所有操作通过卷积完成，卷积操作具有平移不变性

  • 旋转只会导致角旋转发生变化，特征值保持不变。角点具有旋转不变性

  • 将仿射强度变化(颜色值的变化)定义为：𝐼𝑛𝑒𝑤 = 𝛼𝐼𝑜𝑙𝑑 + β(𝛼是对比度，β是明暗)。二阶矩矩阵 M 只取决于导数，所以 β 无关。但是，α 影响图像导数的缩放，并且存在阈值。角点对仿射强度变化部分不变

  • 角点不随缩放而等变。欲使角点随缩放而等变，则可以使用高斯金字塔在尺度空间中执行 Harris 检测

image.png

Blobs(图像色块检测)

  • Limitations of Points and Edges：

    1. Edge难以被定位
    2. 角点可以被定位但是描述性低

  • Blobs：图像色块，是数字图像中与周围区域相比在属性（如亮度或颜色）上不同的区域

  • Blob 具有固定的位置和大小，可以localized，是很好的interest points

  • Blob detection是SIFT feature的前身

  • 1D Blobs：和周围不一样，有两条边夹着Blobs,可以通过Edge detection完成Blobs检测

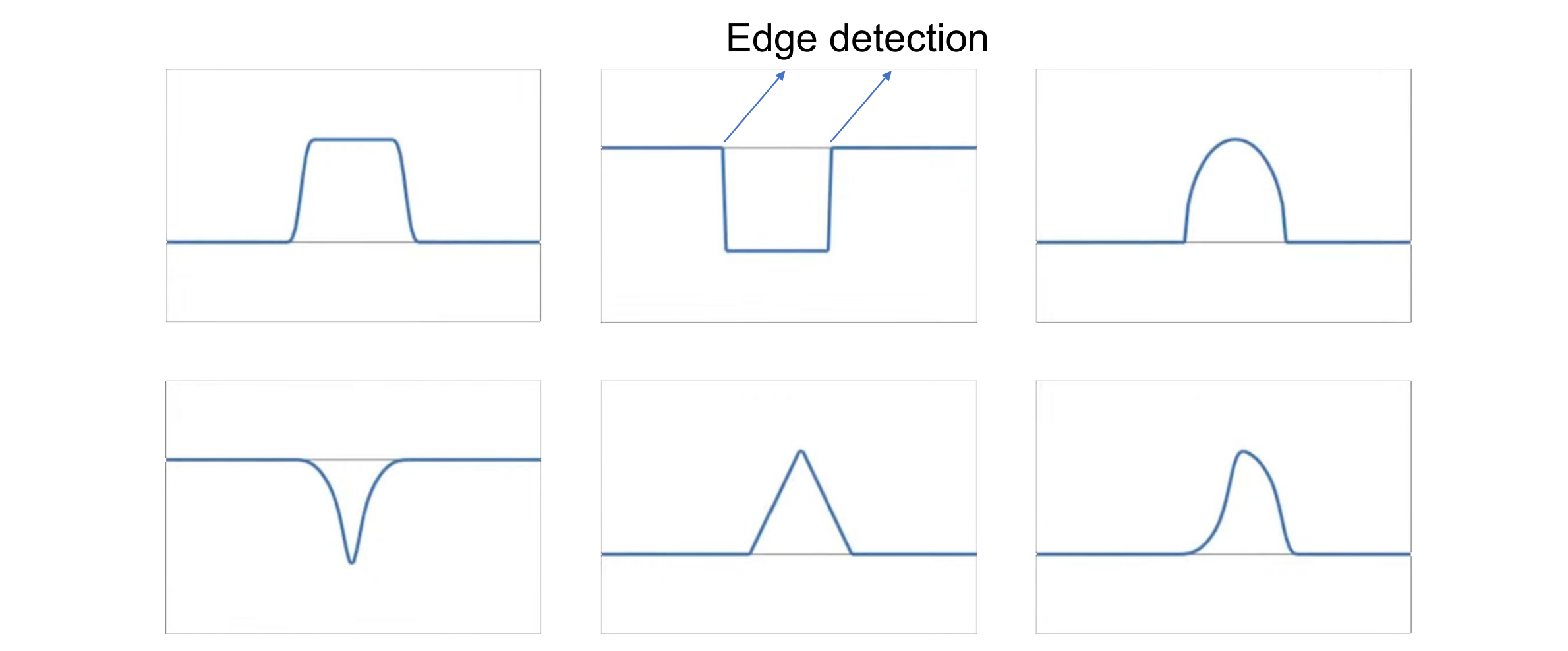
image.png

高斯梯度下的 Edge Detection

  • Filtering with convolution:𝑓 ∗ ℎ = ∫ 𝑓(𝜏) ℎ(𝑥 − 𝜏) 𝑑𝜏,其中*是卷积操作

  • Calculate gradient for edge detection:

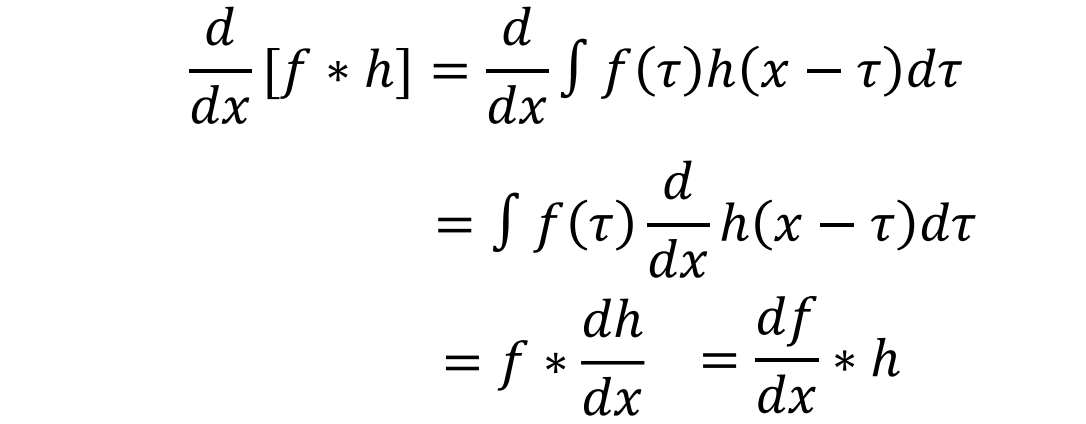
image.png

  • Extremum of 𝑓 ∗ ℎ′ is an edge：设𝑓(𝑥) = 𝑢(𝑥 − 𝑥0)为阶跃函数,ℎ(𝑥) = 𝐺𝛿(𝑥) is a Gaussian function:𝑓 ∗ ℎ′= 𝑓 ∗ ℎ′= 𝑓′∗ ℎ= 𝐺𝛿(𝑥) ∗ 𝛿(𝑥 − 𝑥0)= 𝐺𝛿(𝑥 − 𝑥0)

  • The edge is at the location of 𝑥:

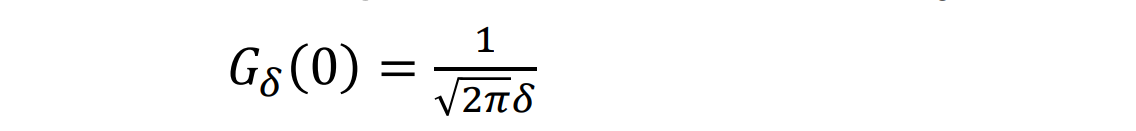
image.png

  • 使用归一化高斯导数不依赖于 δ(冲击函数，采样函数) 的极值，即 f ∗ δ Gδ’

二阶高斯梯度下的 Edge Detection

  • Extremum of 𝑓 ∗ ℎ′ is an edge → Zero-crossing of 𝑓 ∗ ℎ′′ is an edge

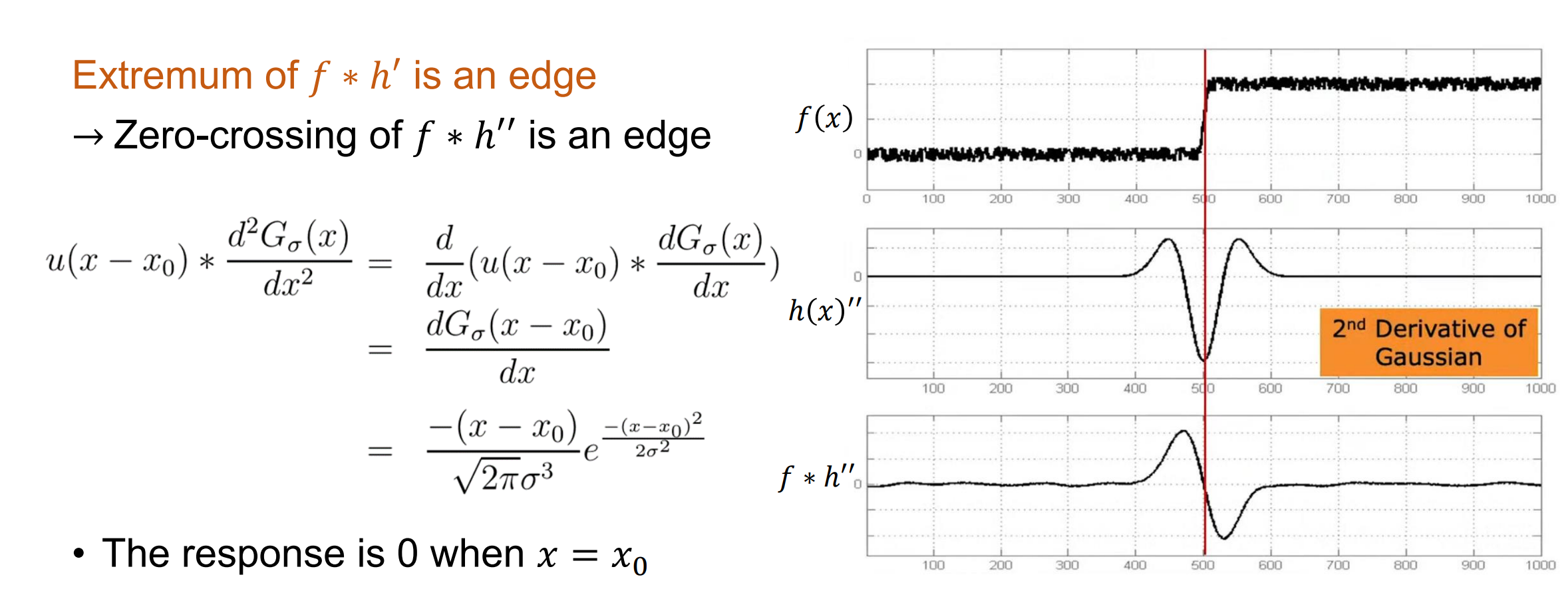
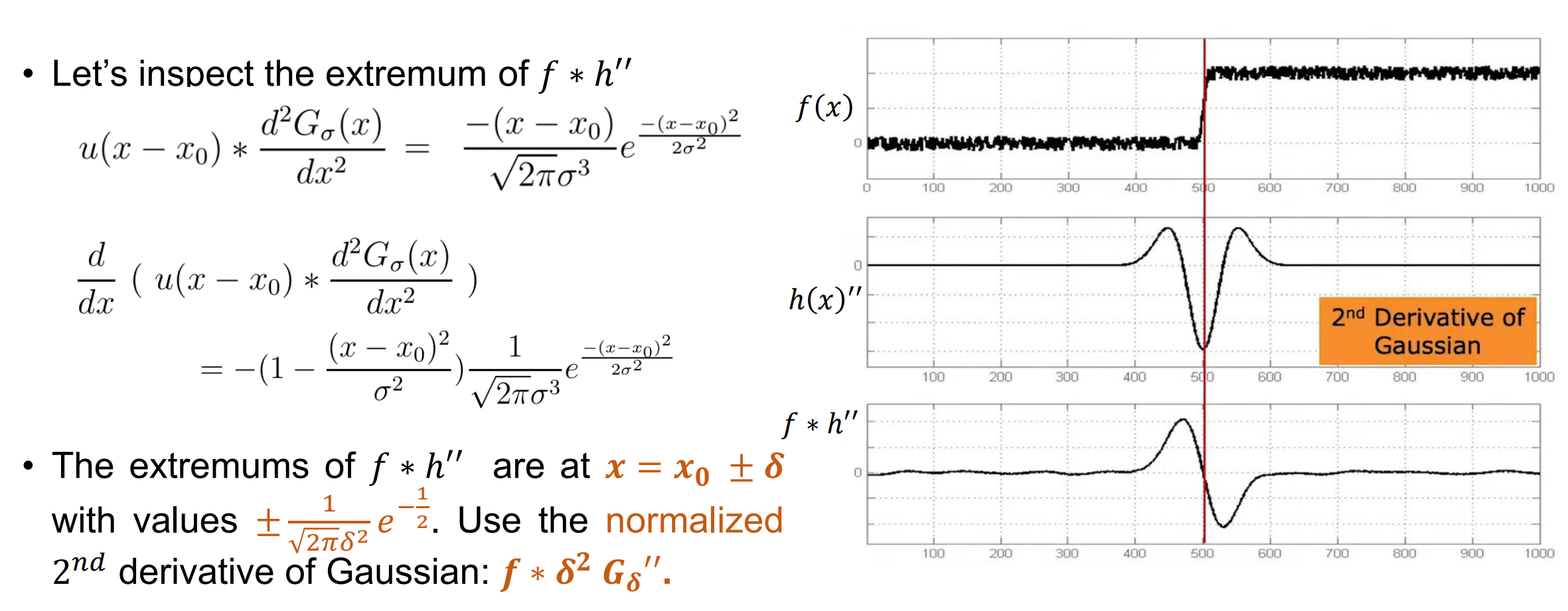
image.png

image.png

二阶高斯梯度下的 Blobs Detection

  • Blob小，极值点加强。一个边两个极值。与之匹配的机制σ是Blob的大小，极值σ的位置是Blob的位置。图像随着σ的变化而变化

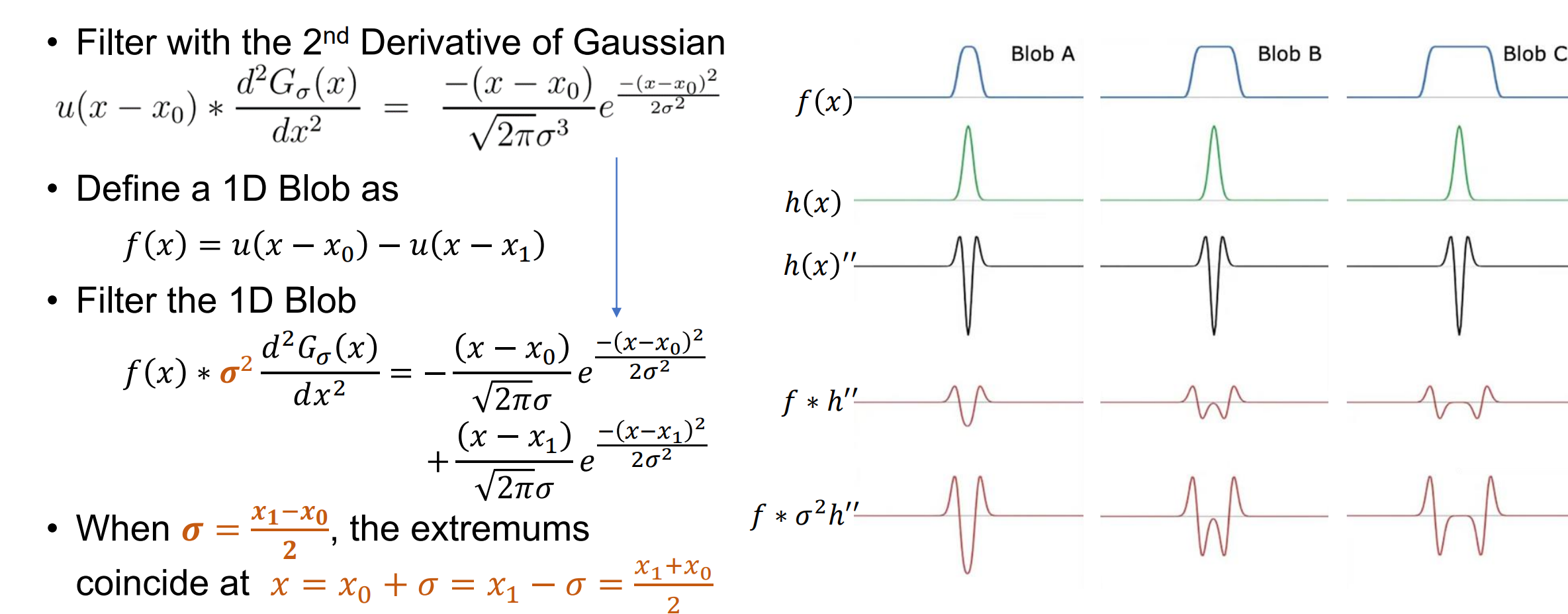
image.png

  • Summary of 1D Blob Detection：

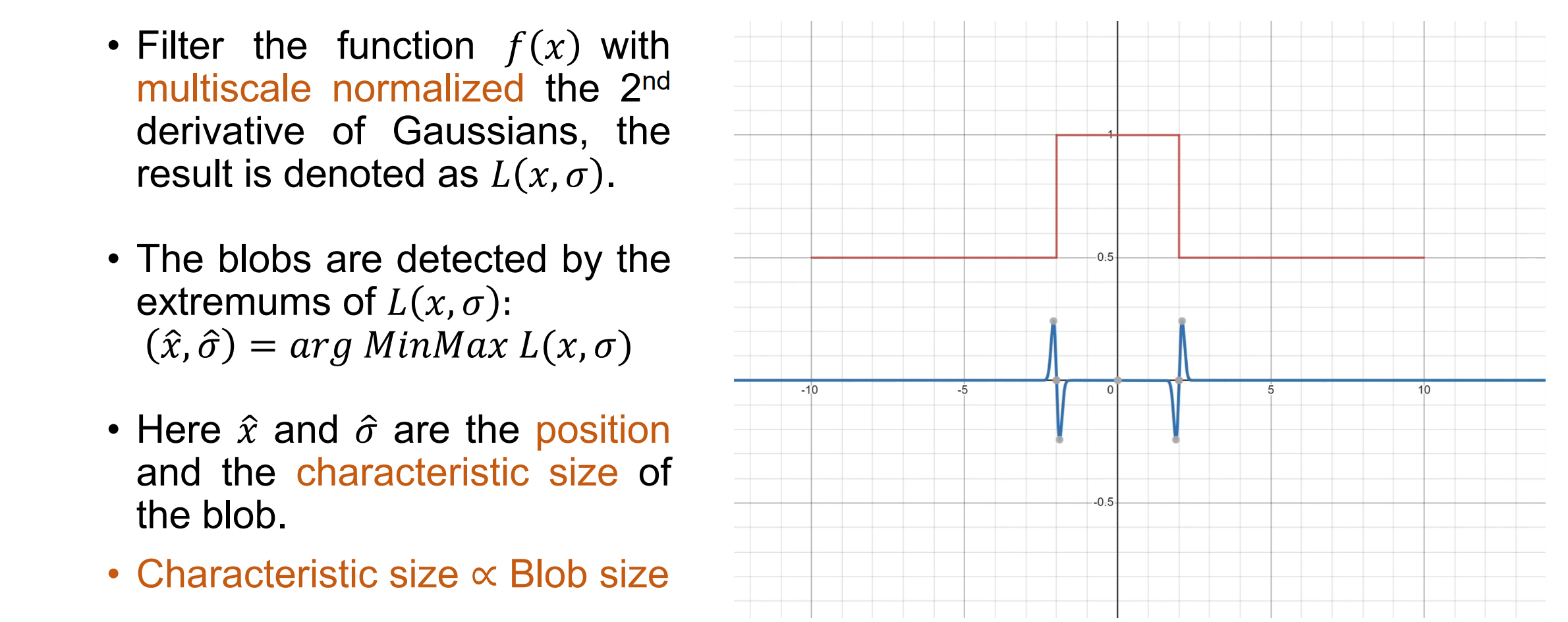
image.png

2D Blob Detection: Laplacian of Gaussian

  • 直观地说，我们可以用高斯的二阶导数 G′′（x; σ） 在 x 方向上检测Blob，然后用 G′′ (y;σ) 在 y 方向上检测Blob;，然后对两个方向求和

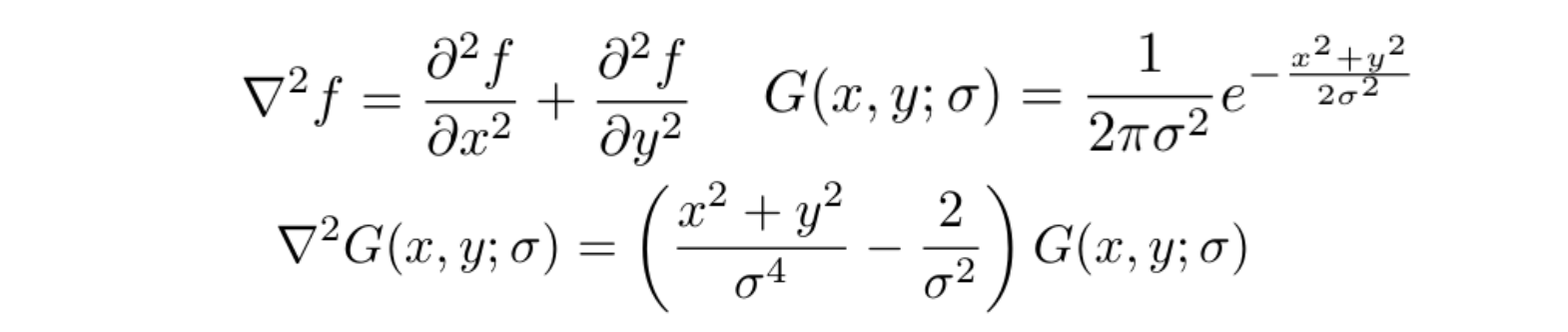
image.png

  • 可以使用多尺度高斯归一化拉普拉斯算力（NLoG： σ²∇²G x， y;σ ）来检测二维Blob，即过滤具有不同σ值的图像，并提取极值

2D Blob Detection: Scale Selection

  • 给定一个二进制圆和尺度为 σ 的 NLoG 滤波器，我们可以将结果计算为尺度 I（x， y; σ） 的函数：

image.png

  • Summary of 2D Blob Detection：

image.png

SIFT Feature

  • 尺度不变关键点的显著图像特征

  • 将Blob作为尺度不变的关键点:

    1. 通过提取多尺度 NLoG 的极值来检测Blob
    2. 如果重新缩放了Blob，仍然可以在 NLoG 的移位滤波输出中检测到
    3. 在缩放归一化后，我们使Blob缩放不变
    4. Blob对旋转、遮挡、杂波或噪声也很鲁棒

Fast NLoG Approximation: DoG

  • 高斯差值 （DoG） 是高斯归一化拉普拉斯量 （LoG） 的近似值和快速实现

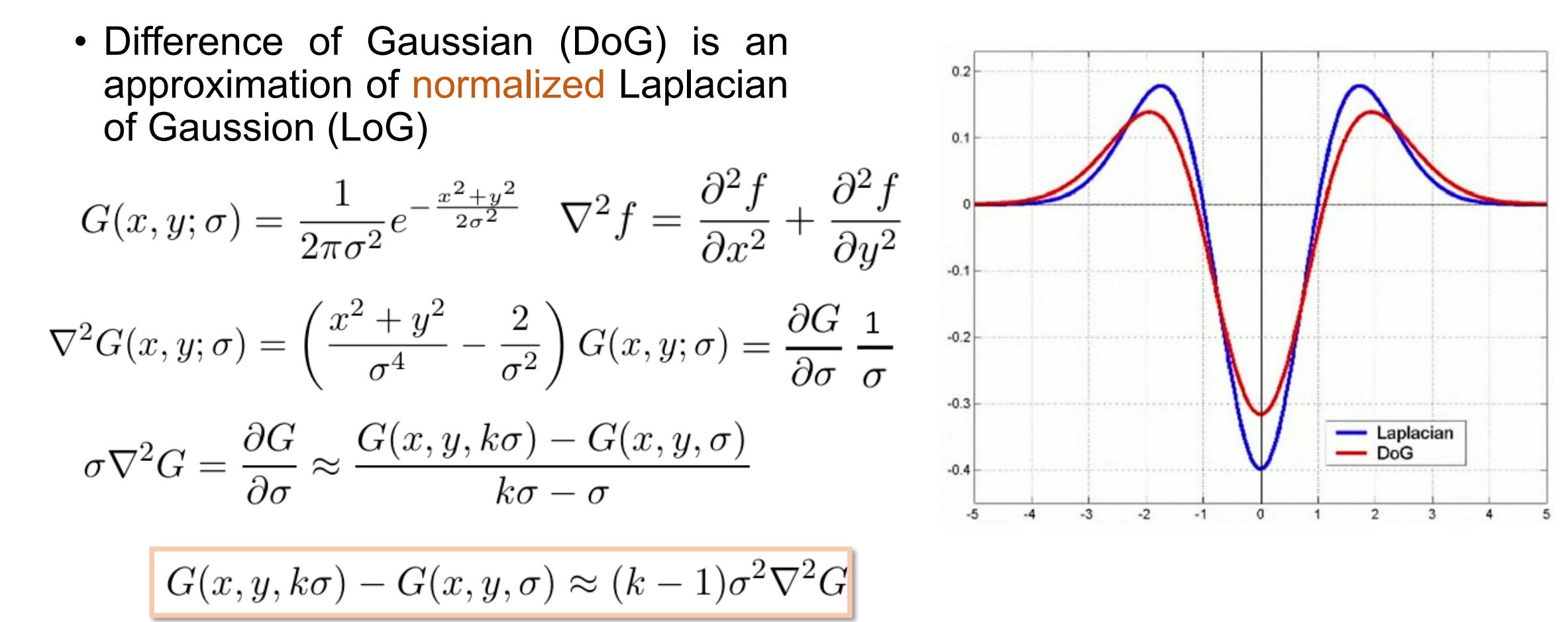
image.png

Blob Detection with the Image Pyramid

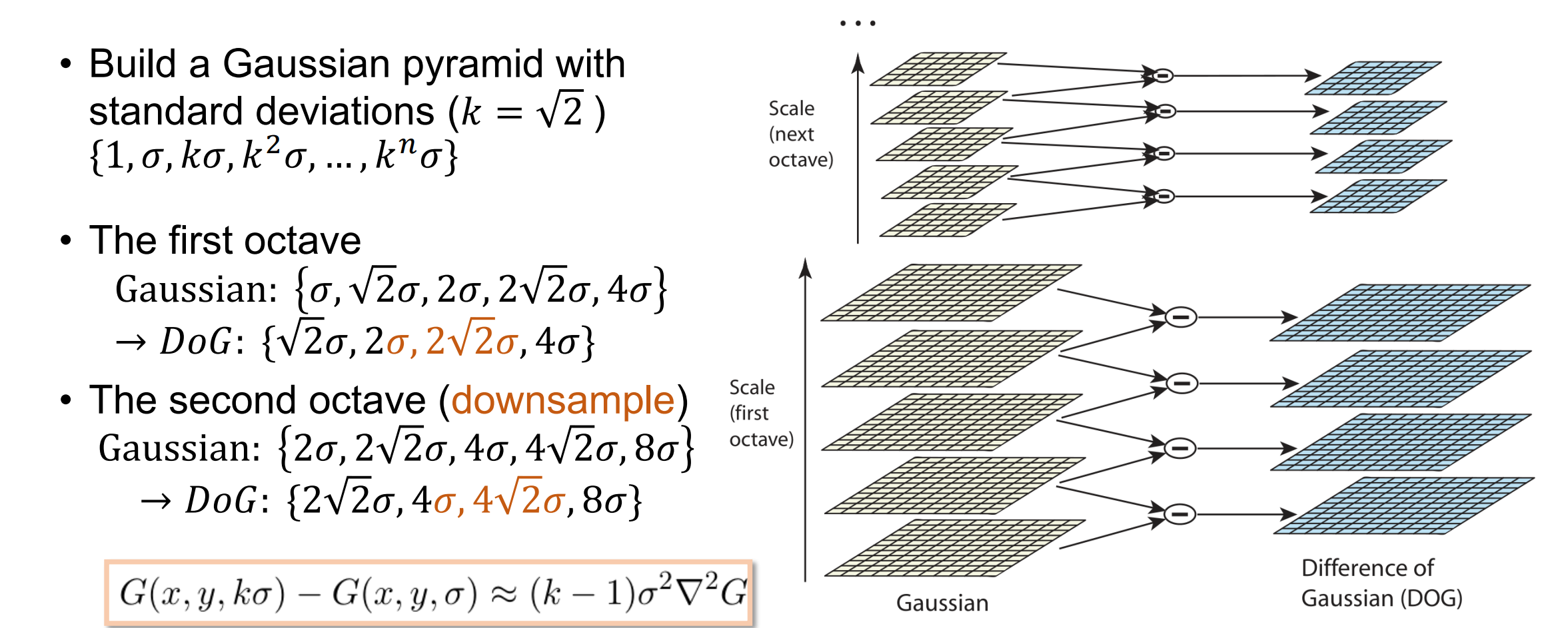
image.png

  • 通过在当前和相邻比例（用圆圈标记）下将像素与 3x3x3 区域中的 26 个相邻像素进行比较来检测 DoG 图像的极值

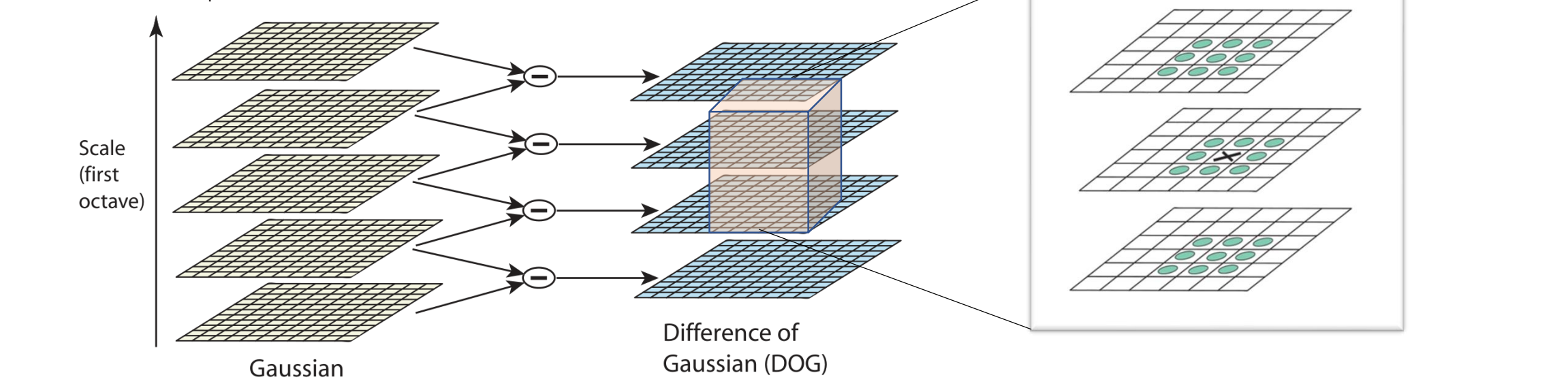
image.png

Blob Keypoint Selection

image.png

Computing the Principal Orientation of the Feature(计算特征的主方向)

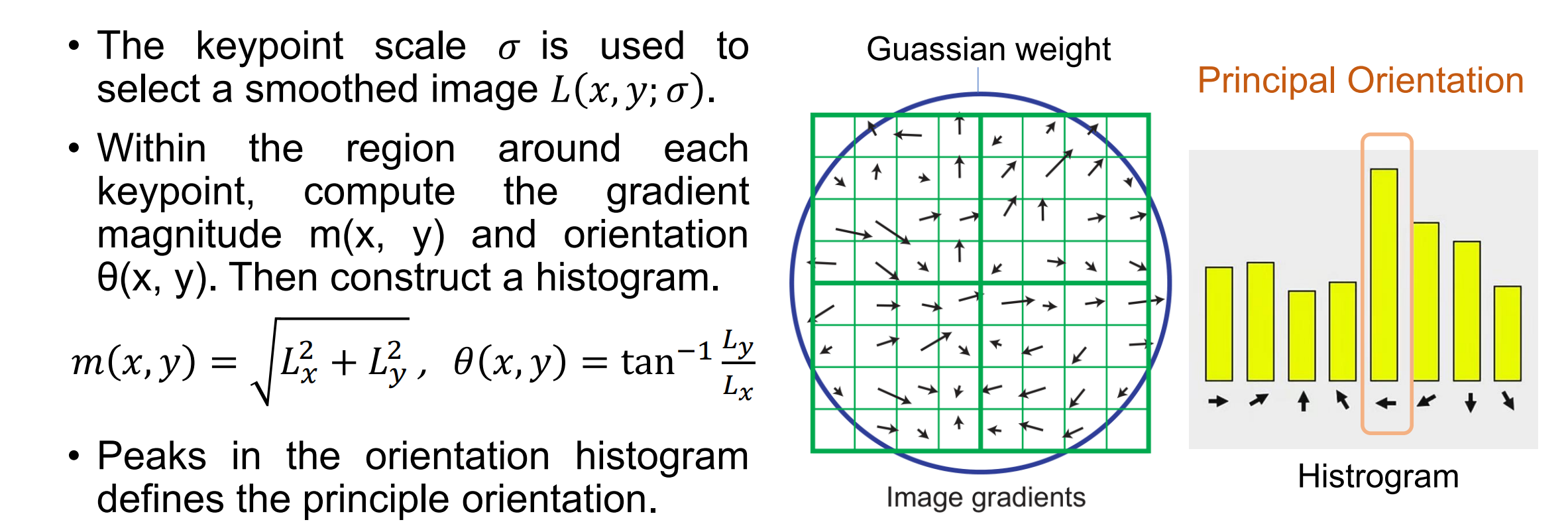
image.png

  • 通过计算梯度的方向和幅度来构建梯度方向直方图，选择梯度方向直方图中的峰值方向作为特征的主方向

  • 可以用主方向来消除旋转带来的变化

  • 可以使用梯度直方图作为描述符，实施细节：

    1. 使用关键点的缩放来选择图像的高斯模糊级别
    2. 预先计算金字塔所有级别的梯度以提高效率
    3. 使用高斯窗口（蓝色圆圈）以避免突然变化
    4. 将特征标准化为单位长度以减少照明的影响
    5. 在实践中，使用 4x4 本地窗口，每个窗口有 8 个方向，因此维度为 128

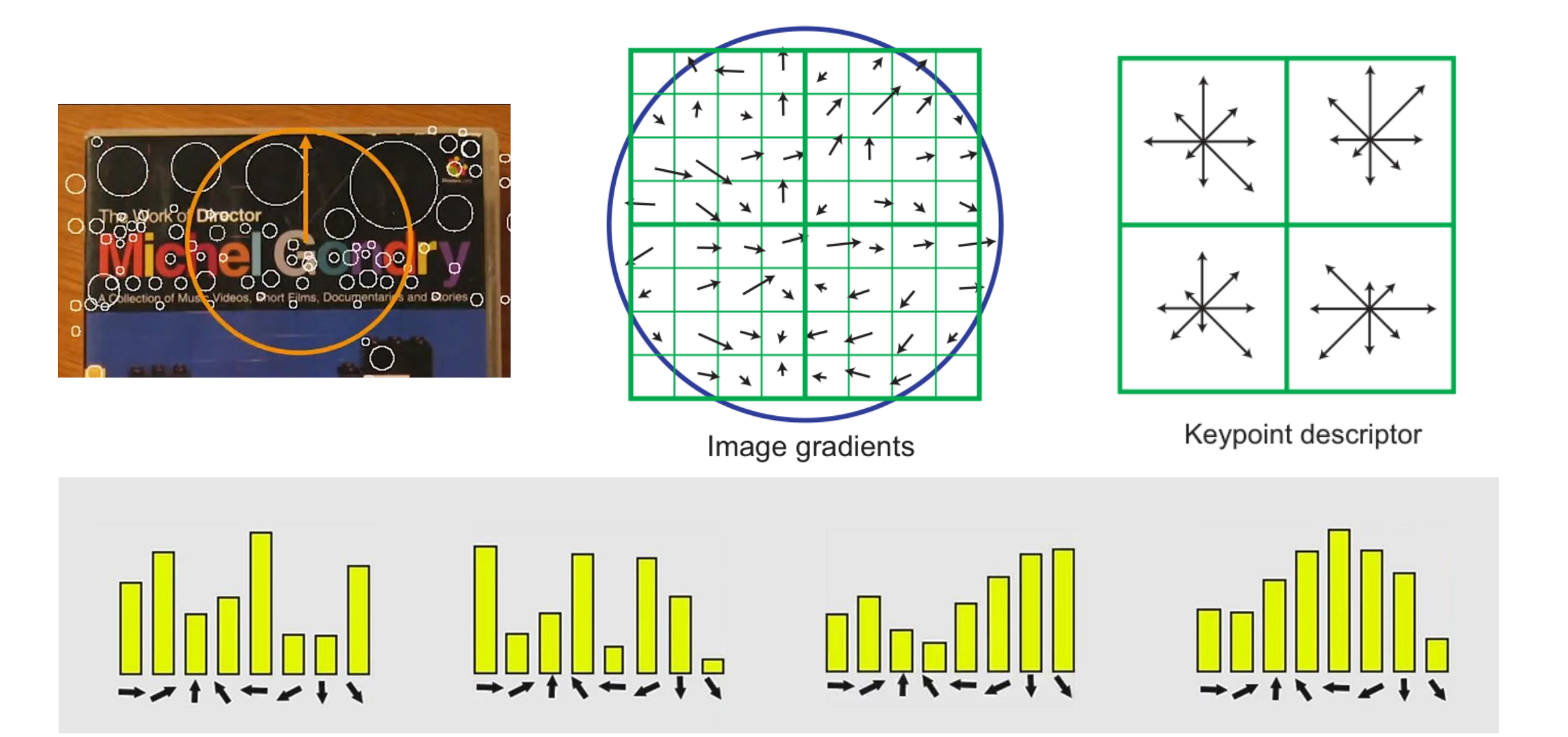
image.png

  • Summary of SIFT：

image.png

Histogram of Oriented Gradients (HoG) Feature

  • 局部物体的外观和形状可以通过梯度分布来表征，甚至无需精确了解梯度位置：

    1. 将图像大小调整为 128x64，并计算每个像素的梯度
    2. 将无符号梯度（幅度和角度）划分为 8x8 个单元格，并计算 9 点直方图
    3. 将 2x2 单元格分组，步幅为 1
    4. 标准化直方图（对照明和阴影具有鲁棒性）

  • HoG vs SIFT：

    1. 对于计算：
      1. HoG 特征以单一比例在密集网格中计算，而不进行主导方向对齐
      2. SIFT 特征在一组稀疏的比例不变关键点处计算，旋转以对齐其主导方向
    2. 对于用法：
      1. SIFT 功能针对稀疏宽基线匹配进行了优化
      2. HOG 功能用于空间形式的密集稳健编码

HoG Feature for Detection

  • 提取 HoG 特征并训练线性分类器 （SVM）

  • 使用具有不同尺度的滑动窗口运行分类器