数据结构与算法A 第三章栈与队列

• 栈和队列是典型的线性结构，常被称为“操作受限的线性表”或“限制存取点的线性表”

栈

• 栈是一种限定仅在限制在一端进行插入和删除的线性表，无论是插入元素还是删除读取栈中的元素，都只能固定在线性表的一断进行。这一端被称为栈顶(top)，另一端叫做栈底(bottom)

• 最后插入栈中的元素是最先被删除或读取的元素，而最先压入的元素则被放在栈的底部。栈的修改是按后进先出的原则进行(Last-In First-Out，LIFO)，也称“下推表”

• push操作：往栈中插入元素，简称压栈或入栈；pop操作：删除栈顶元素，简称出栈或弹出

栈的ADT

template <class T> 		// 栈的元素类型为 T
class Stack 
{ 
    public: 	        			// 栈的运算集
        void clear();			// 变为空栈
        bool push(const T item); 	// item入栈,成功则返回真,否则返回假
        bool pop(T & item);	// 返回栈顶内容并弹出,成功返回真,否则返回假
        bool top(T& item);	// 返回栈顶内容但不弹出,成功返回真,否则返回假
        bool isEmpty(); 		// 若栈已空返回真
        bool isFull();  		// 若栈已满返回真
};

顺序栈

• 顺序栈：采用顺序存储结构的栈，需要一块连续的区域来存储栈中的元素

• 顺序栈本质上简化的顺序表,对元素数目为n的栈，首先需要确定哪一端表示栈顶

  1. 0位置作为栈顶：插入和删除都在第0个位置进行，push和pop都需要把当前栈的所有元素在数组中后移或前移一个，时间代价O(n)
  2. n-1位置作为栈顶，只需将新元素添加到表尾，出栈也只需删除表尾，时间代价O(1)

• 顺序栈实现时，整型变量top既可以只是当前的栈顶位置，也可以表示当前栈中的元素的个数

template <class T>
class arrStack : public Stack <T> 
{
    private: 	              	  // 栈的顺序存储
        int mSize;	    	  // 栈中最多可存放的元素个数
        int top;		  // 栈顶位置，应小于mSize
        T *st;		  // 存放栈元素的数组
    public:   		    	  // 栈的运算的顺序实现
        arrStack(int size) 
        { 	// 创建顺序栈实例		
            mSize = size;
            st = new T[mSize]; 
            top = -1;
        }
    arrStack() 
    { 		// 创建一个顺序栈的实例 
        top = -1;
    }	
    ~arrStack() 
    {		// 析构函数
        delete [] st;
    }
    void clear() 
    {		// 清空栈内容
        top = -1;
    }
};

• top可以有两种定义方式

  1. 设置为栈中第一个空闲位置，即空栈的top=0
  2. 把top定义为栈中最上面的那个元素的位置，而非第一个空闲位置，top=-1或任何非自然数

• push一个元素首先把top+1，然后把新元素插入到新的栈顶位置。同样pop先删除栈顶元素，再把top-1

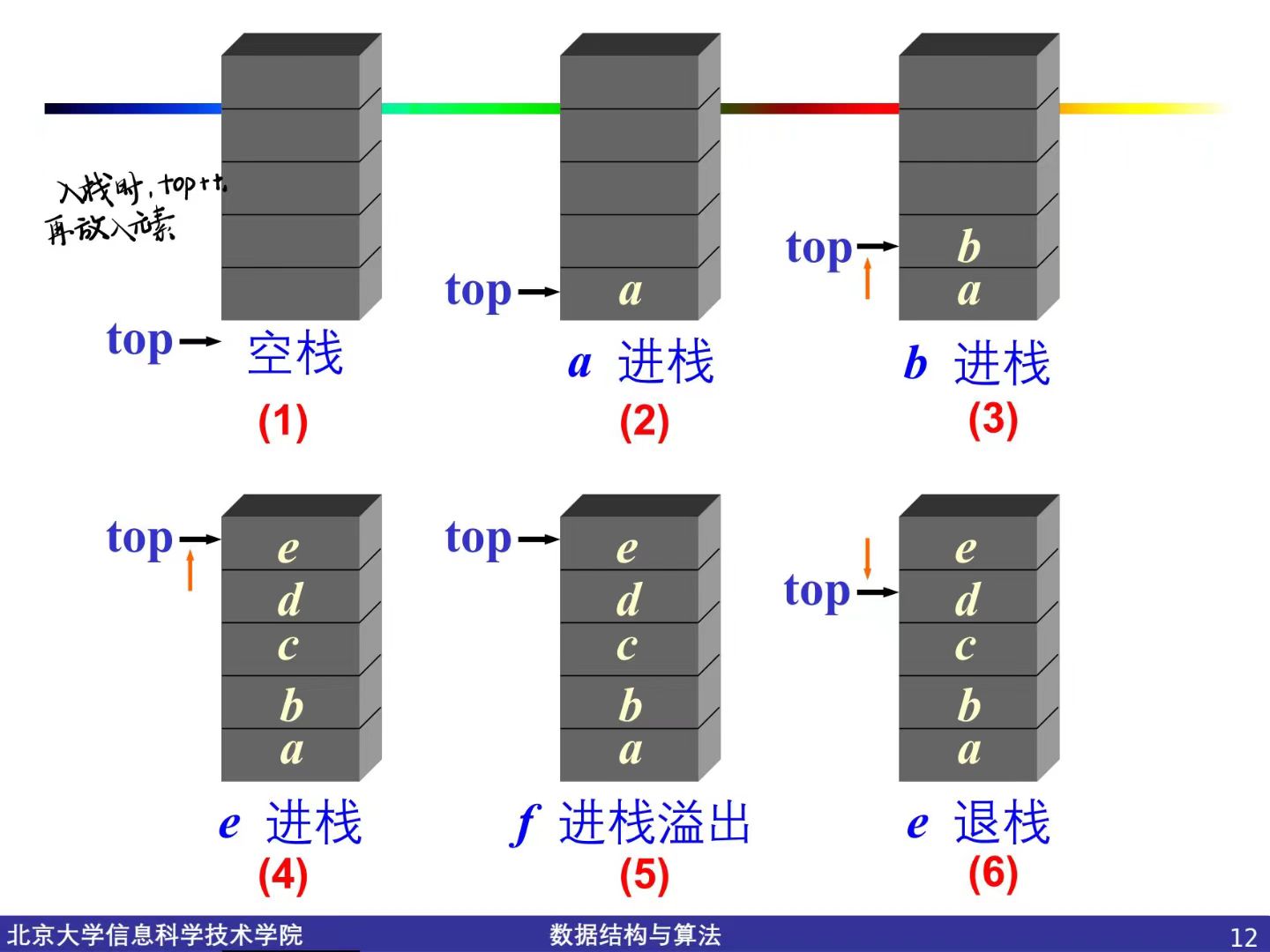
• 顺序栈的溢出：

  1. 当栈中已有mSize个元素时，进栈操作会产生上溢出(overflow)
  2. 在空栈上进行出栈操作则会造成下溢出(underflow)

• 入栈

bool arrStack<T>::push(const T item) 
{
    if (top == mSize-1) 
    {  		// 栈已满 
        cout << "栈满溢出" << endl;
        return false;
    }
    else 
    {		                         // 新元素入栈并修改栈顶指针
        st[++top] = item;                //“先执行++，而后执行进栈操作！”
        return true;
    }
}

• 出栈

bool arrStack<T>::pop(T & item) 
{	// 出栈的顺序实现
    if (top == -1) 
    {		       // 栈为空
        cout << "栈为空，不能执行出栈操作"<< endl; 
        return false;
    }
    else 
    {
        item = st[top--];	        // 返回栈顶元素并修改栈顶指针 
        return true;
    }
}

• 读取栈顶

bool arrStack<T>:: top(T & item) 
{	// 返回栈顶内容，但不弹出
    if (top == -1) 
    {			// 栈空
        cout << " 栈为空，不能读取栈顶元素"<< endl; 
        return false;
    }
    else 
    { 						
        item = st[top];
        return true;
    }
}	 

• 清空栈

void  arrStack<T>::clear() 
{
    top = -1;
}

• 判断栈满

bool arrStack<T>:: isFull() 
{
    return  (top == mSize-1);
}

• 双栈共享一个栈空间

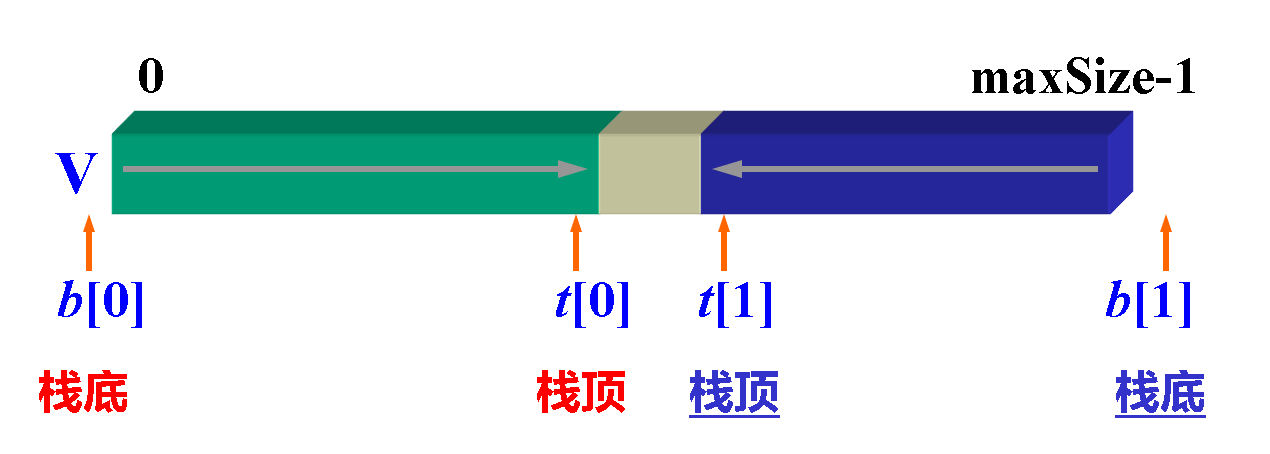
链式栈

• 链式栈本质上是简化的链表，为了方便读取，栈顶元素是链表头。指针方向：从栈顶到栈底

• 只能在链表头部进行操作，故链表没有必要像单链表那样附加头结点(head)，栈顶指针就是链表的头指针（top）

• 无栈满问题（但存在栈空约束）

• push和pop操作的时间代价均为O(1)

• 栈的链式实现

template <class T> 
class lnkStack : public Stack <T>  
{ 
    private: 				// 栈的链式存储
        Link<T>* top;			// 指向栈顶的指针
        int size;			// 存放有效元素的个数
    public:                      	// 栈运算的链式实现
        lnkStack(int defSize) 
        {   // 构造函数
            top = NULL;
            size = 0;
        }
    ~lnkStack() 
    {	// 析构函数
        clear();
    }
};

• 压栈

// 入栈操作的链式实现	
bool lnkStack<T>:: push(const T item) 
{ 	    	
    //创建一个新节点，并使其next域赋值top;
    Link<T>* tmp = new Link<T>(item, top);
    top = tmp;
    size++;
    return true;
}

• 出栈

bool lnkStack<T>:: pop(T& item) 
{// 出栈操作的链式实现
    Link <T> *tmp;
    if (size == 0) 
    {
        cout << "栈为空，不能执行出栈操作"<< endl; 
        return false;
    } 
    item = top->data; 
    tmp = top->next;
    delete top;
    top = tmp;
    size--;
    return true;
}

• 顺序栈和链式栈的比较:

  1. 时间效率：所有操作都只需常数时间，顺序栈和链式栈在时间效率上难分伯仲
  2. 空间效率：顺序栈须说明一个固定的长度；链式栈的长度可变，但增加结构性开销

• 栈的应用：

  1. 递归
  2. 表达式求值

表达式求值

• 表达式是由常量、变量、运算符、函数调用按一定规则组合而成的

• 表达式的组成：

  1. 基本符号集：由{0，1，…，9，+，-，*，/，（，）} 等16个基本符号组成
  2. 语法成分集：由{ <表达式> , <项> , <因子> , <常数> , <数字> } 5个语法成分组成
  3. 语法公式集 ：“::=”是规则定义符

中缀表达式

• 表达式的分类：

  1. 中缀表示：<操作数> <操作符> <操作数>，如 A+B
  2. 前缀表示：<操作符> <操作数> <操作数>，如 +AB
  3. 后缀表示：<操作数> <操作数> <操作符>，如 AB+

• 中缀表达式的递归定义：

  1. <表达式> ∷ = <项> + <项> | <项> － <项> | <项>
  2. <项> ∷ = <因子> * <因子> |<因子> / <因子> |<因子>
  3. <因子> ∷ = <常数> | （ <表达式> ）
  4. <常数> ∷ = <数字> |<数字> <常数>
  5. <数字> ∷ = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9

• 中缀表达式的计算次序

  1. 先执行括号内的计算，后执行括号外的计算，在具有多层括号时，按层次反复地脱括号
  2. 在无括号或同层括号时，先乘(*) 、除(／)，后作加(+)、减(-)
  3. 在同一个层次，若有多个乘除（*、／）或加减 (+，-)的运算，那就按自左至右顺序执行

后缀表达式

• 后缀表达式（逆波兰式）不含括号，所有求值计算皆按运算符出现的顺序，严格从左向右进行

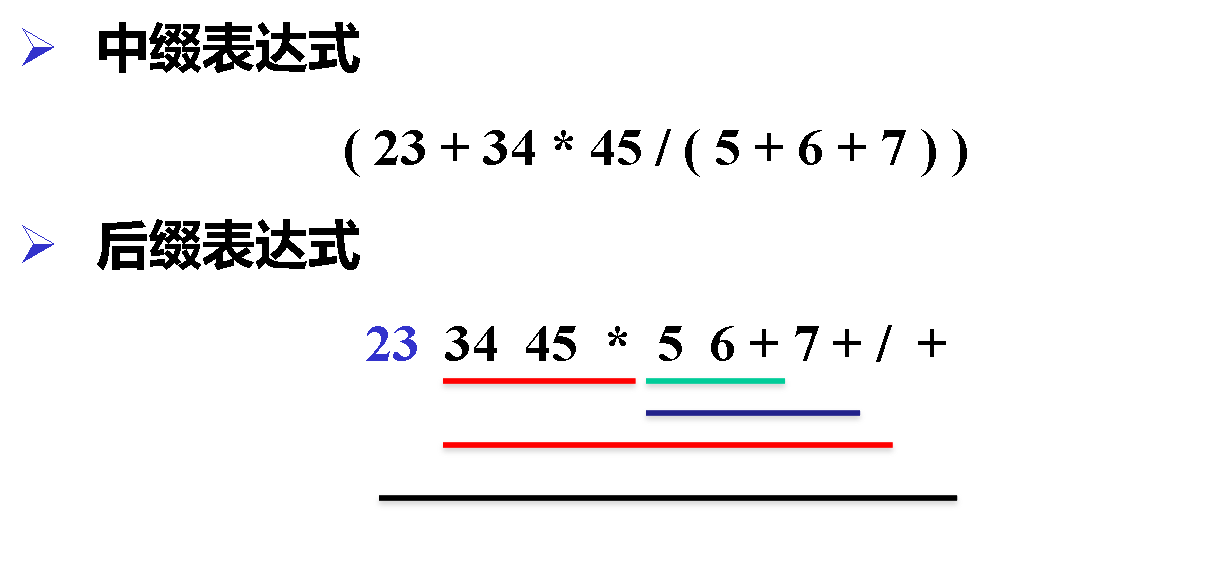
中缀表达式到后缀表达式的转换

• 关键在于如何恰当地去掉中缀表达式中的括号，此过程中用栈储存有关的元素

• 思路：用栈来存放表达式中的操作数、开括号以及在这个开括号后面的其他暂时不能确定计算次序的内容

  1. 当输入是操作数，直接输出到后缀表达式序列
  2. 当输入的是左括号时，也把它压栈
  3. 当输入的是运算符时,While (以下循环)
     If（栈非空 and 栈顶不是左括号 and 输入运算符的优先级 “≤”栈顶运算符的优先级）时
     将当前栈顶元素弹栈，放到后缀表达式序列中（此步反复循环，直到上述if条件不成立）; 将输入的运算符压入栈中。
     Else 把输入的运算符压栈（>当前栈顶运算符才压栈！）
  4. 当输入的是右括号时，先判断栈是否为空
     若为空（括号不匹配），异常处理，清栈退出；
     若非空，则把栈中的元素依次弹出
     遇到第一个左括号为止，将弹出的元素输出到后缀表达式的序列中（弹出的开括号不放到序列中）
     若没有遇到开括号，说明括号也不匹配，做异常处理，清栈退出
  5. 最后，当中缀表达式的符号序列全部读入时，若栈内仍有元素，把它们全部依次弹出，都放到后缀表达式序列尾部

后缀表达式求值

• 思路：利用栈来记录后缀表达式中的两个操作数
  1. 当遇到的是操作数，则压入栈顶
  2. 当遇到的是运算符, 就从栈中两次取出栈顶，按照运算符对这两个操作数进行计算。然后将计算结果压入栈顶
  3. 如此继续，直到遇到符号＝, 这时栈顶的值就是输入表达式的值

// Class Declaration 类的说明
class Calculator  
{ 
    private:
        Stack<double> s;	// 这个栈用于压入保存操作数
        bool GetTwoOperands(double& opd1,double& opd2); // 从弹出两个操作数
        void Compute(char op); // 取两个操作数，并按op对两个操作数进行计算
    public:
        Calculator(void){} ;	// 创建计算器实例，开辟一个空栈
        void Run(void);	// 读入后缀表达式，遇到符号"="时，求值计算结束 
        void Clear(void);   	// 计算器的清除，为随后的下一次计算做准备  
};

bool Calculator::GetTwoOperands(double& opd1, double& opd2)  
{ 
    if (s.isEmpty()) 
    {
        cerr << "Missing operand!" <<endl;
        return false;
    }
    s.pop(&opd1); 				// 右操作数
    if (s.isEmpty())  
    {
        cerr << "Missing operand!" <<endl;
        return false;
    }
    s.pop(&opd2);			// 左操作数
    return true;
}

void Calculator::Compute（char op）
{
    Boolean result;
    double operand1, operand2;
    result = GetTwoOperands(operand1,operand2);
    if(result == True)
        switch(op)
        {      
            case '+': S.Push(operand2 + operand1);
                break; 
            case '-': S.Push(operand2 - operand1);
                break;
            case '*': S.Push(operand2 * operand1);
                break;
            case '/’: if(operand1 == 0.0)
                {
                    cerr<<"Divided by 0!"<<endl;
                    S.ClearStack();
                } 
                else
                    S.Push(operand2 / operand1);
                break;
        }
    else
        S.ClearStack();  
}

void Calculator::Run(void)
//读入表达式，遇到操作数则入栈，遇到操作符则从栈中连续弹出两个操作数计算，直至遇到“=”结束。
{
    char c;
    double newoperand;
    while(cin>>c, c != '=')  
    {
        case '+': 
        case '-': 
        case '*':
        case '/': 
            Compute(c);
            break;
        default:
            cin.pushback(c);
                           cin >> newoperand;
            S.push(newoperand);
            break;
    }
    if (!S.IsEmpty())
        cout << S.top()  << endl; //印出求值的最后结果
}  //end calculator::run(void)
    
void Calculator::Clear(void)
{
    S.ClearStack();
}

栈与递归

• 递归：在调用一个函数的过程中又直接调用或间接调用了函数自身

• 递归的组成

  1. 递归基础(递归出口)：保证递归结束的前提
  2. 递归规则：确定了由简单情况构筑复杂情况需要遵循的规则

• 函数运行时的存储分配

  1. 静态分配
     a. 在非递归情况下，数据区的分配可以在程序运行前进行，一直到整个程序运行结束才释放，这种分配称为静态分配
     b. 采用静态分配时，函数的调用和返回处理比较简单，不需要每次分配和释放被调函数的数据区
  2. 动态分配
     a. 在递归（函数）调用的情况下，被调函数的局部变量不能静态地分配某些固定单元，而必须每调用一次就分配一份，以存放当前所使用的数据，当返回时随即释放。【大小不确定，值不确定】
     b. 动态分配在内存中开辟一个称为运行栈的足够大的动态区

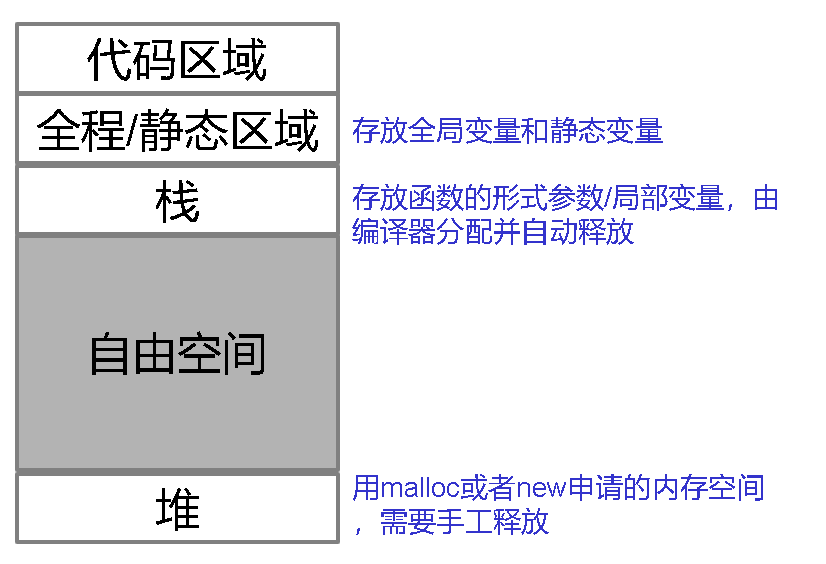
• 动态存储分配：用作动态数据分配的存储区，分为堆（heap）和栈（stack）

  1. 堆区域则用于不符合LIFO（诸如指针的分配）的动态分配
  2. 栈用于分配发生在后进先出LIFO风格中的数据（诸如函数的调用）

• 运行栈又称活动记录栈也称调用栈

  1. 调用一个函数时，执行进栈操作，把被调函数所对应的活动记录分配在站的顶部
  2. 从函数返回时，执行出栈操作，释放本次的活动记录，恢复到上次调用所分配的数据区中

• 一个函数在运行栈上可以有若干不同的活动记录，每个都代表了一个不同的调用

队列

• 队列也是一种限制访问点的线性表。队列的元素只能从表的一端插入，另一端删除。把只允许删除的一端称为队列的头，简称队头，把删除操作称为出队。称表的另一端为队列的尾，简称队尾，这一端只能进行插入操作，称为入队

• 队列的特性：先进先出(FIFO, First In First Out)

队列的ADT

template <class T>  
class Queue  
{ 
public: 			        // 队列的运算集
    void clear();			// 变为空队列
    bool enQueue(const T item); 	// 将item插入队尾，成功则返回真，否则返回假
    bool deQueue(T& item);     	        // 返回队头元素并将其从队列中删除，成功则返回真
    bool getFront(T& item);	        // 返回队头元素，但不删除，成功则返回真
    bool isEmpty(); 		        // 返回真，若队列已空
    bool isFull();       		// 返回真，若队列已满
};

顺序队列

• 用顺序存储结构实现队列就形成了顺序队列，需要分配一块连续的区域来存储队列的元素，需要事先知道大小

• 顺序队列也存在溢出问题，队列满时入队会产生上溢，队列为空时出队则会产生下溢

• 用向量存储队列元素，用两个变量分别指向队列的前端(front)和尾端(rear)

  1. front：指向当前待出队的元素位置（地址）
  2. rear： 指向当前待入队的元素位置（地址）

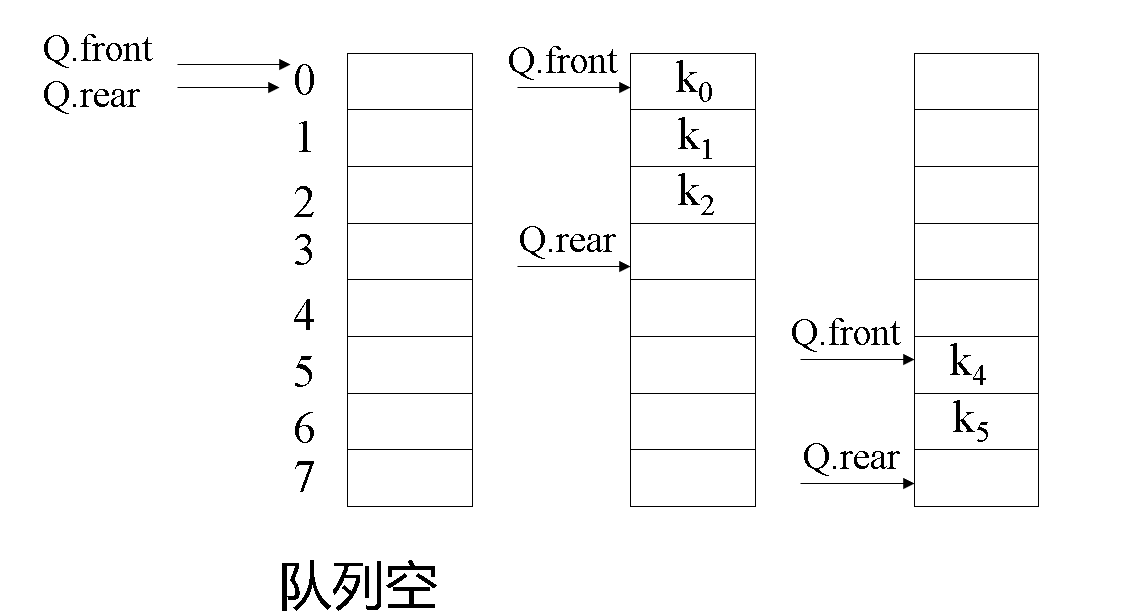
• 假溢出：当 rear = mSize-1 时，再作插入运算就会产生溢出，如果这时队列的前端还有许多空位置，这种现象称为假溢出

• 队列的类定义

class arrQueue: public Queue<T> 
{ 
    private: 	
        int mSize; 			// 存放队列的数组的大小
        int front;			// 表示队头所在位置的下标
        int rear;			// 表示待入队元素所在位置的下标
        T *qu;                          // 存放类型为T的队列元素的数组
    public: 				// 队列的运算集
        arrQueue(int size)  
        {   // 创建队列的实例		
            mSize = size +1;              // 浪费一个存储空间，以区别队列空和队列满
            qu = new T [mSize];
            front = rear = 0;
        }
        ~arrQueue()  
        {   // 消除该实例，并释放其空间
            delete [] qu;
        }
}

• 入队列操作

bool arrQueue<T> :: enQueue(const T item)  
{   //  item入队，插入队尾
    if (((rear + 1 ) % mSize) == front) 
    {
        cout << "队列已满，溢出" << endl;
        return false;
    }
    qu[rear] = item;
    rear = (rear +1) % mSize;  		// 循环后继
    return true;
}

• 出队列操作

bool arrQueue<T> :: deQueue(T& item)  
{   // 返回队头元素并从队列中删除
    if (front == rear)  
    {
        cout << "队列为空" << endl;
        return false;
    }
    item = qu[front];
    front = (front + 1) % mSize;
    return true;
}

链式队列

• 链式队列是队列的链式实现，是对链表的简化。链接的方向从队列的前端指向队列的尾端。成员front和rear是分别指向队首和队尾的指针，增加成员size来表示队列中当前元素的个数

• 链式队列在进队时无队满问题，但有队空问题。队空条件： front == rear==NULL

• 队列的类定义

template <class T> 
class lnkQueue: public Queue <T> 
{ 
    private: 	
        int size; 	// 队列中当前元素的个数
        Link<T>* front;	// 表示队头的指针
        Link<T>* rear;	// 表示队尾的指针
    public: 				// 队列的运算集
    lnkQueue(int size)  
    {   			// 创建队列的实例
        size = 0;
        front = rear = NULL;
    }
    ~lnkQueue()  
    {  		// 消除该实例，并释放其空间
        clear();
    }
};

• 入队

bool lnkQueue <T> :: enQueue(const T item) 
{ //  入队插入队尾
    if (rear == NULL) 	
    {	// 空队列
        front = rear = new Link<T> (item, NULL);
    }
    else  
    {   // 添加新的元素
        rear-> next = new Link<T> (item, NULL);  
        rear = rear ->next;
    }
    size++;
    return true;
}

• 出队

// 返回队头元素并从队列中删除
bool lnkQueue <T> :: deQueue(T& item)  
{          			
    Link<T> *tmp;
    if (size == 0)  
    {    // 队列为空，没有元素可出队
        cout << "队列为空" << endl;
        return false;
    }
    &item = front->data; 
    tmp = front;
    front = front -> next;
    delete tmp;
    if (front == NULL)
        rear = NULL;
    size--;
    return true;
}

• 顺序队列和链式队列的比较
  1. 由于存储空间固定，顺序队列无法满足队列规模变化很大且最大规模无法预测的情况，而链式队列可以轻松应对这种类型的应用
  2. 时间效率：顺序队列和链式队列中常用的入队和出队操作都需要常数时间，二者无优劣之分
  3. 空间效率：顺序队列长度固定，不能再一个数组中存储两个队列

限制存取点的表

• 变种的栈或队列结构
  1. 双端队列：在队首和队尾都可以插入、删除的队列
  2. 双栈：两个底部相连的栈，共享一块数据空间
  3. 超队列：是一种被限制的双端队列，删除操作只允许在一端进行，插入操作却可以在两端同时进行
  4. 超栈：是一种插入受限的双端队列，即插入限制在一端而删除仍允许在两端进行

---

第三章 栈与队列 OJ作业

1:滑动窗口

/*描述
给定一个长度为n（n<=10^6）的数组。有一个大小为k的滑动窗口从数组的最左端移动到最右端。你可以看到窗口中的k个数字。窗口每次向右滑动一个数字的距离。
下面是一个例子：
数组是 [1 3 -1 -3 5 3 6 7]， k = 3。
窗口位置	最小值	最大值
[1  3  -1] -3  5  3  6  7 	-1	3
 1 [3  -1  -3] 5  3  6  7 	-3	3
 1  3 [-1  -3  5] 3  6  7 	-3	5
 1  3  -1 [-3  5  3] 6  7 	-3	5
 1  3  -1  -3 [5  3  6] 7 	3	6
 1  3  -1  -3  5 [3  6  7]	3	7
你的任务是得到滑动窗口在每个位置时的最大值和最小值。
输入
输入包括两行。
第一行包括n和k，分别表示数组的长度和窗口的大小。
第二行包括n个数字。
输出
输出包括两行。
第一行包括窗口从左至右移动的每个位置的最小值。
第二行包括窗口从左至右移动的每个位置的最大值。
样例输入
8 3
1 3 -1 -3 5 3 6 7
样例输出
-1 -3 -3 -3 3 3
3 3 5 5 6 7*/
#include <iostream>
#include <vector>
#include <deque>
using namespace std;
int main()
{
    int n, k;
    cin >> n >> k;
    vector<int> a(n);
    for (int i = 0; i < n; i++)
    {
        cin >> a[i];
    }
    vector<int> minValues(n - k + 1);
    vector<int> maxValues(n - k + 1);
    deque<int> minDeque, maxDeque;

    for (int index = 0; index < n; index++)
    {
        // 清理出界的元素,如果队列不为空并且队首元素的索引已经不在当前窗口内，则移除队首元素
        if (!minDeque.empty() && minDeque.front() == index - k)
        {
            minDeque.pop_front();
        }
        if (!maxDeque.empty() && maxDeque.front() == index - k)
        {
            maxDeque.pop_front();
        }

        // 更新最小值队列
        while (!minDeque.empty() && a[minDeque.back()] >= a[index])
        {
            minDeque.pop_back();
        }
        minDeque.push_back(index);

        while (!maxDeque.empty() && a[maxDeque.back()] <= a[index])
        {
            maxDeque.pop_back();
        }
        maxDeque.push_back(index);

        if (index >= k - 1)
        {
            minValues[index - k + 1] = a[minDeque.front()];
            maxValues[index - k + 1] = a[maxDeque.front()];
        }
    }

    for (int x : minValues)
    {
        cout << x << " ";
    }
    cout << endl;
    for (int x : maxValues)
    {
        cout << x << " ";
    }
    cout << endl;

    return 0;
}

2:堆栈基本操作

/*描述
依次读入序列元素1,2,...,n进栈，每进一个元素，机器可要求下一个元素进栈或弹栈，如此进行。给定一个输入序列，
判断栈空时弹出的元素构成的序列是否可能等于给定的序列，如果是则输出栈的操作过程，否则输出“NO”。
输入
输入分两行
第一行为n的值（即序列元素个数）
第二行为给定的输入序列（序列元素均为整型）
输出
如果输入序列能够由题目规定的操作得到，则输出对栈的操作过程
否则直接输出“NO”
样例输入
7
4 5 3 6 2 7 1
样例输出
PUSH 1
PUSH 2
PUSH 3
PUSH 4
PUSH 5
POP 5
POP 3
PUSH 6
POP 6
POP 2
PUSH 7
POP 7
POP 1
提示
给定序列中有可能有不在1...n之间的数字*/
#include <iostream>
#include <stack>
#include <vector>
using namespace std;
int main()
{
    int n;
    cin >> n;
    vector<int> target(n);
    for (int i = 0; i < n; i++)
    {
        cin >> target[i];
    }
    stack<int> stk; // 使用栈来模拟
    vector<string> operations;
    int next = 1; // 下一个要进栈的元素索引

    for (int i = 0; i < n; i++)
    {
        // 先把要进栈的元素进栈，直到栈顶元素等于当前目标元素
        while (next <= n && (stk.empty() || stk.top() != target[i]))
        {
            operations.push_back("PUSH " + to_string(next));
            stk.push(next);
            next++;
        }
        // 如果栈顶元素与当前目标元素相等，则弹出
        if (!stk.empty() && stk.top() == target[i])
        {
            operations.push_back("POP " + to_string(stk.top()));
            stk.pop();
        }
        else
        {
            cout << "NO" << endl;
            return 0;
        }
    }
    for (const string &op : operations)
    {
        cout << op << endl;
    }
    return 0;
}

3:中缀表达式的值

/*描述
人们熟悉的四则运算表达式称为中缀表达式，例如(23+34*45/(5+6+7))。在程序设计语言中，可以利用堆栈的方法把中缀表达式转换成保值的后缀表达式（又称逆波兰表示法），
并最终变为计算机可以直接执行的指令，得到表达式的值。
给定一个中缀表达式，编写程序，利用堆栈的方法，计算表达式的值。
输入
第一行为测试数据的组数N
接下来的N行，每行是一个中缀表达式。表达式中只含数字、四则运算符和圆括号，操作数都是正整数，数和运算符、括号之间没有空格。中缀表达式的字符串长度不超过600。
输出
对每一组测试数据输出一行，为表达式的值
样例输入
3
3+5*8
(3+5)*8
(23+34*45/(5+6+7))
样例输出
43
64
108
提示
注意：运算过程均为整数运算（除法运算'/'即按照C++定义的int除以int的结果，测试数据不会出现除数为0的情况），输出结果也为整数（可能为负）。
中间计算结果可能为负。*/
#include <iostream>
#include <stack>
#include <string>
#include <cctype>
#include <sstream>
#include <vector>
#include <map>

using namespace std;

// 运算符优先级
map<char, int> precedence = {
    {'+', 1},
    {'-', 1},
    {'*', 2},
    {'/', 2}};

// 判断是否是运算符
bool isOperator(char c)
{
    return precedence.count(c) > 0;
}

// 将中缀表达式转换为后缀表达式
vector<string> infixToPostfix(const string &infix)
{
    stack<char> operators;
    vector<string> output;
    for (size_t i = 0; i < infix.length(); ++i)
    {
        char c = infix[i];
        if (isdigit(c))
        {
            string number;
            while (i < infix.length() && isdigit(infix[i]))
            {
                number += infix[i++];
            }
            output.push_back(number);
            --i; // 退回一个字符，因为for循环会自增
        }
        else if (c == '(')
        {
            operators.push(c);
        }
        else if (c == ')')
        {
            while (!operators.empty() && operators.top() != '(')
            {
                output.push_back(string(1, operators.top()));
                operators.pop();
            }
            operators.pop(); // 弹出 '('
        }
        else if (isOperator(c))
        {
            while (!operators.empty() && precedence[operators.top()] >= precedence[c])
            {
                output.push_back(string(1, operators.top()));
                operators.pop();
            }
            operators.push(c);
        }
    }

    while (!operators.empty())
    {
        output.push_back(string(1, operators.top()));
        operators.pop();
    }

    return output;
}

// 计算后缀表达式的值
int Postfix(const vector<string> &postfix)
{
    stack<int> values;

    for (const string &token : postfix)
    {
        if (isdigit(token[0]))
        {
            values.push(stoi(token));
        }
        else
        {
            int b = values.top();
            values.pop();
            int a = values.top();
            values.pop();
            switch (token[0])
            {
            case '+':
                values.push(a + b);
                break;
            case '-':
                values.push(a - b);
                break;
            case '*':
                values.push(a * b);
                break;
            case '/':
                values.push(a / b);
                break;
            }
        }
    }
    return values.top();
}

int main()
{
    int N;
    cin >> N;
    cin.ignore(); // 忽略换行符
    for (int i = 0; i < N; ++i)
    {
        string infix;
        getline(cin, infix);
        vector<string> postfix = infixToPostfix(infix);
        int result = Postfix(postfix);
        cout << result << endl;
    }
    return 0;
}

---