LLM Introduction

什么是大模型

  • 定义：“任何在广泛数据上训练的模型（通常使用大规模的自我监督），可以适应（例如，微调）广泛的下游任务”

image.png

Large Language Models

  • 是Transformer架构的扩展，有数百万/数十亿个参数

  • 通常使用大量 “通用” 文本数据（例如 Web 语料库）进行训练

  • 训练目标通常是“下一个标记预测”：P（Wt+1|WT ，WT-1,…,W1）

  • 随着规模的扩大，会涌现出其他能力（例如，思维链推理）

  • 繁重的计算成本（时间、金钱、GPU）

  • 更大的通用类型：“即插即用”，很少或零次学习：训练一次，然后适应其他任务，无需重新训练。例如，上下文学习和提示

Challenges and Weaknesses of NLP

  • Challenges of NLP:

    1. 文本的离散性
    2. 更困难的数据增强
    3. 文本是“精确”的 - 一个错误的单词会改变句子的全部含义
    4. 可能具有较长的上下文长度和记忆（例如对话）

  • Weaknesses of earlier models/approaches:

    1. 文本长度短
    2. “线性”推理 - 没有attention机制，专注于其他部分
    3. 早期的方法（例如 word2vec）不会根据上下文进行调整

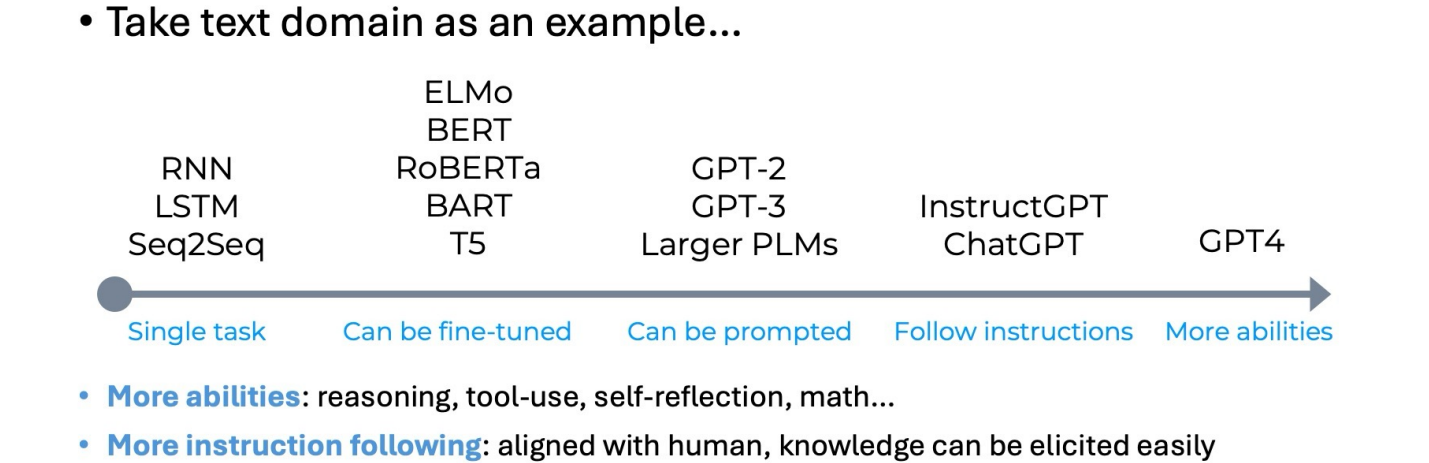
The GPT Stories

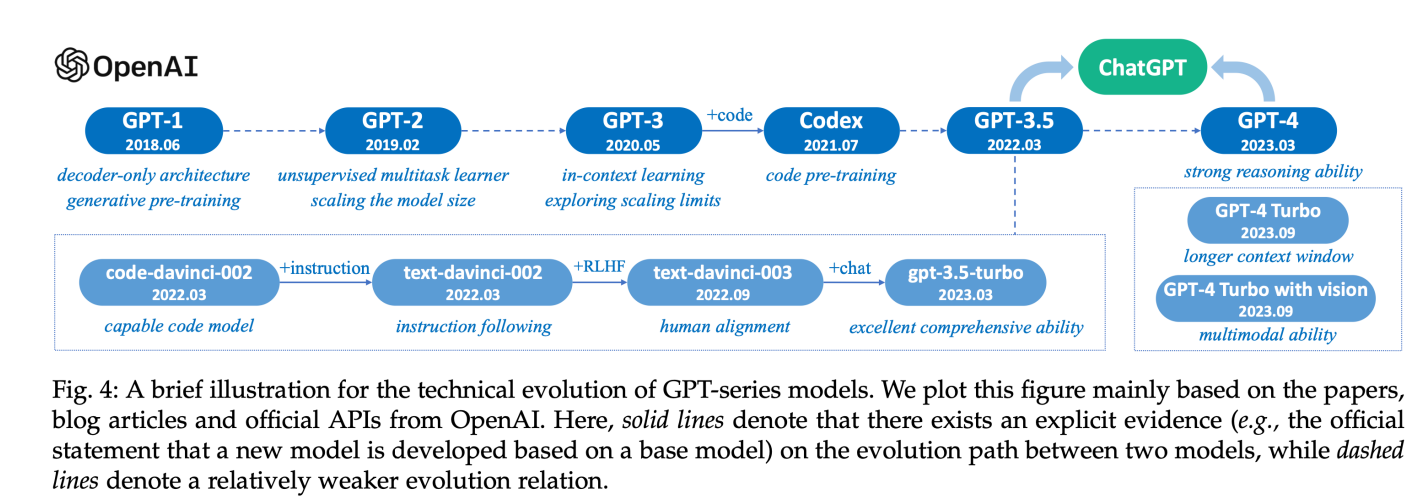
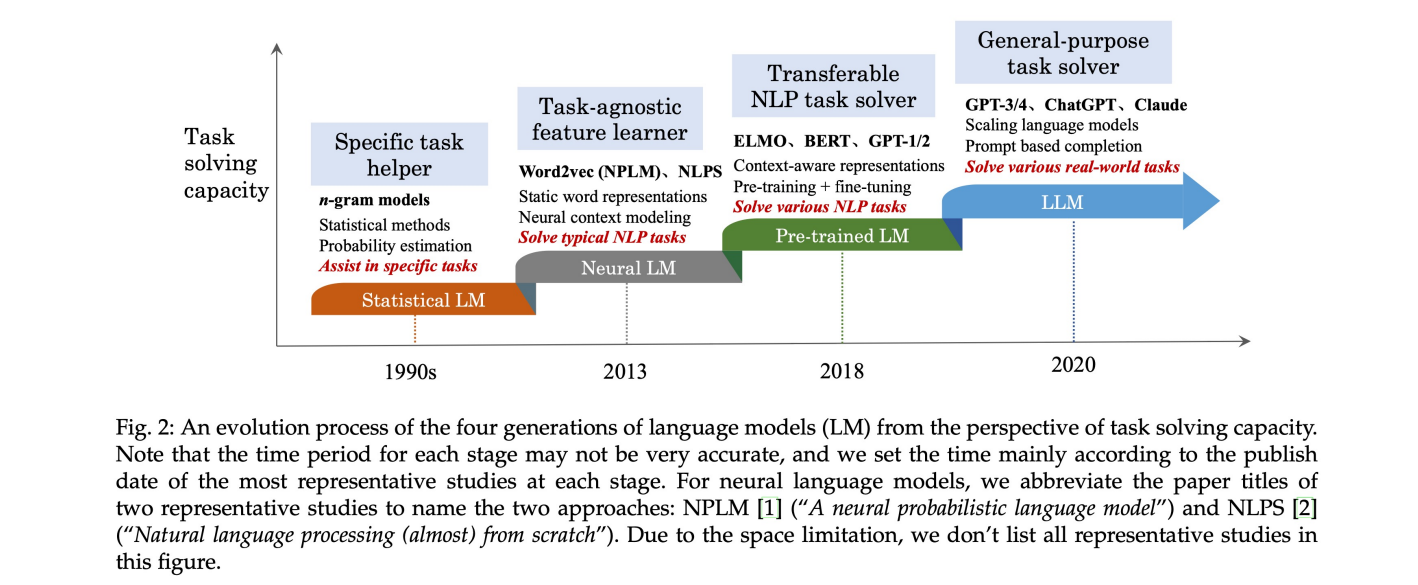
image.png

image.png

The Bitter Lesson

  • Sutton 2019: the only thing that matters in the long run is the leveraging of computation

  • Roughly, 10x more compute every 5 years

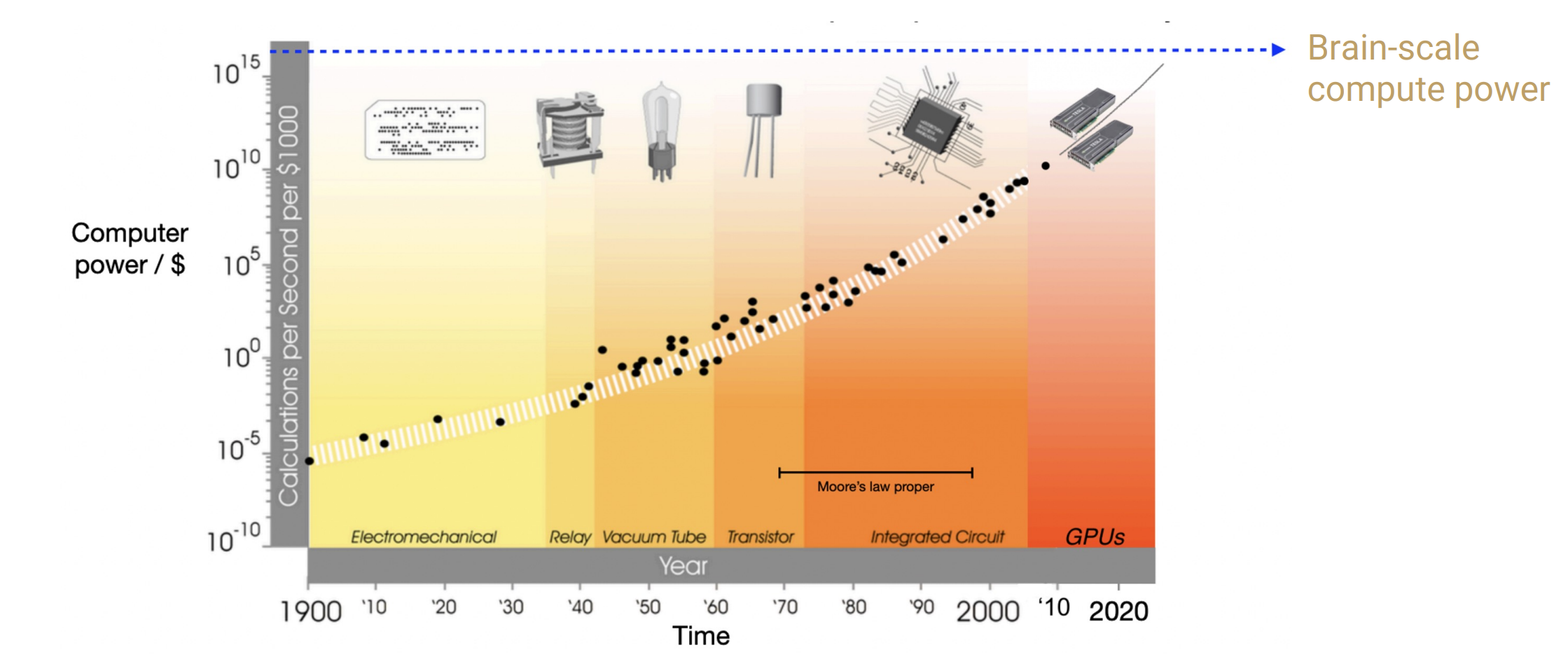
image.png

  • Sutton 2019: 从 70 年的 AI 研究中可以读到的最大教训是，利用计算的通用方法最终是最有效的，而且在很大程度上是最有效的

The Scaling Law

  • N：参数大小;T：训练数据

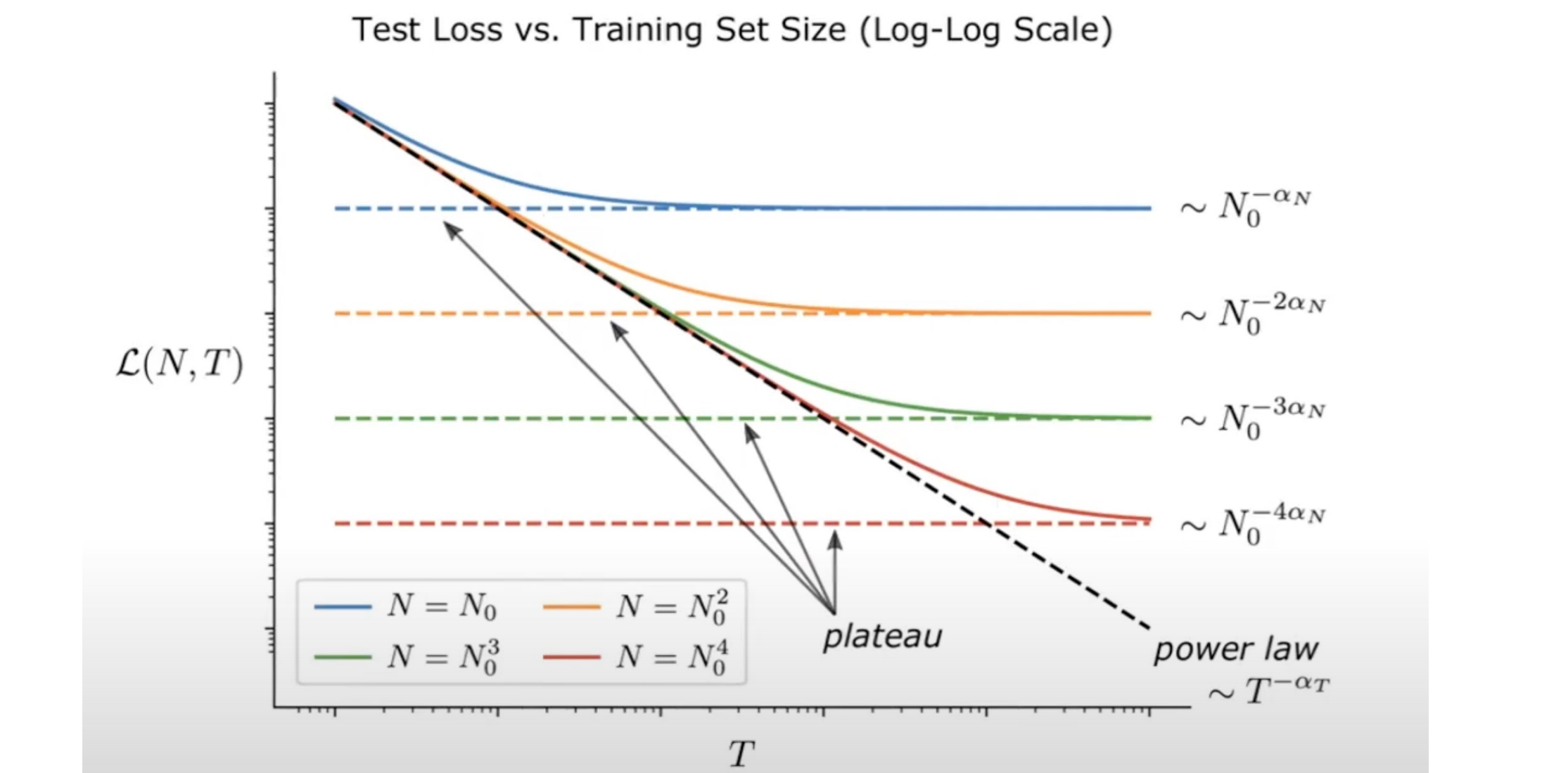
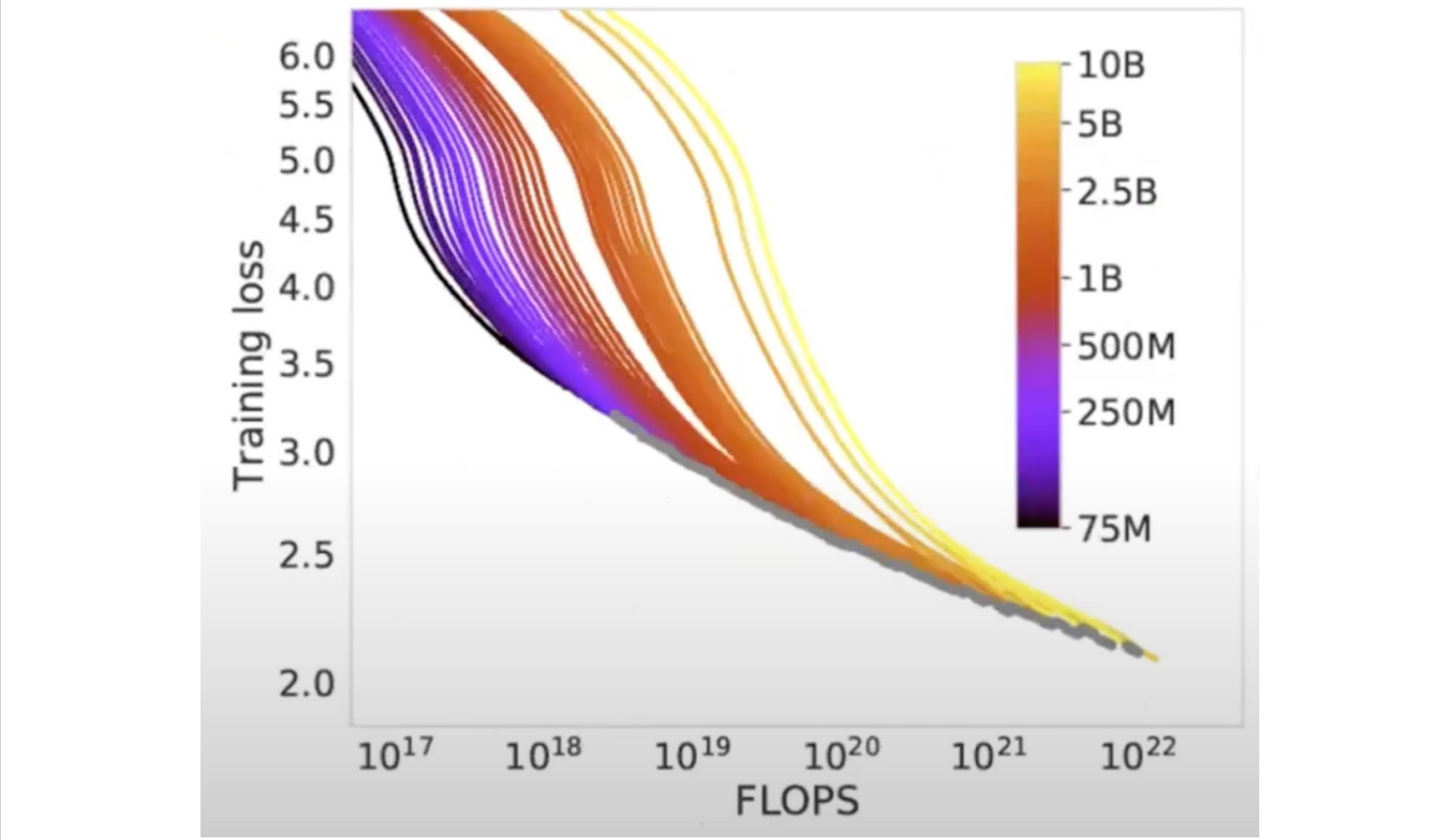
image.png

image.png

  • 图中的训练总是收敛到一条斜线(scaling law)

scaling law的核心变量：

  • 大模型scaling law主要关注以下三个因素：

    1. 参数规模N:模型的参数数量
    2. 数据规模D:训练的token数量
    3. 计算预算C:计算总量(通常用FLOPs计算)

  • scaling law试图回答的问题：

    1. 增加参数量、数据量或计算量，哪个对模型能力的提升最有效？
    2. 是否存在最优的数据量与参数量比例？
    3. 模型的能力提升是否会出现“边际效益递减”(Diminishing Returns)

scaling law的背景

  • scaling laws:在生成模型训练当中呗广泛观察到的现象

  • 对于计算量C、模型参数量N、和数据大小D，当不受到其他两个因素的制约时，模型的性能与每个因素都呈现幂律关系：

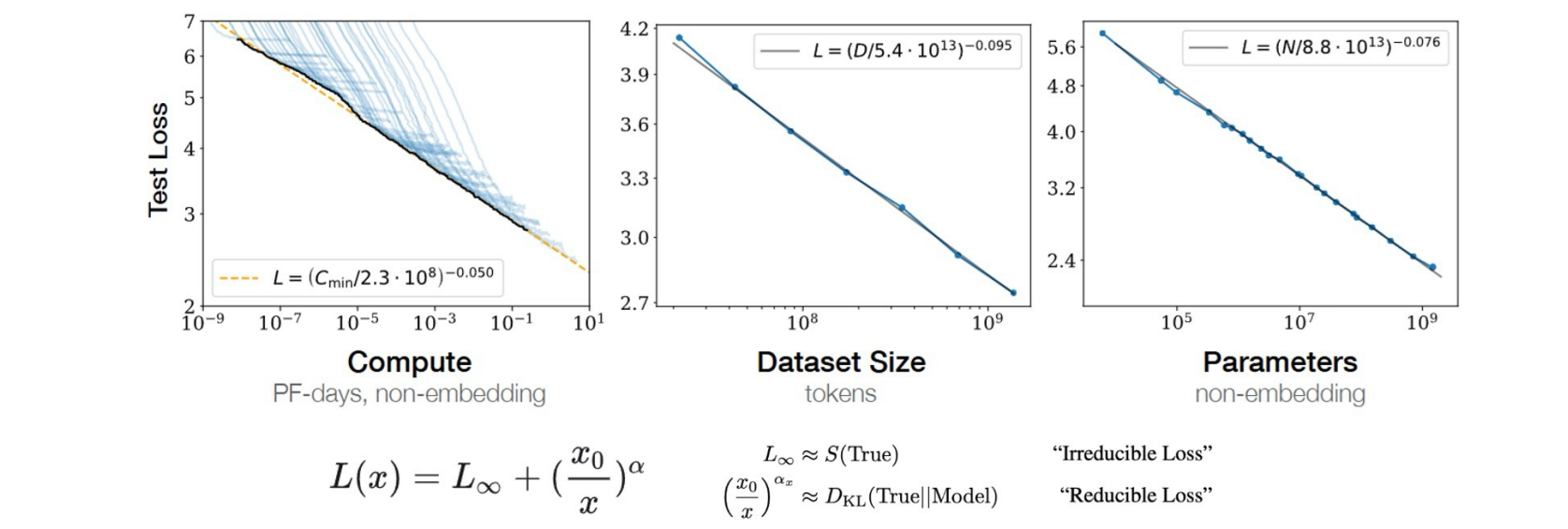
image.png

Compute = 6 * Parameters * Data

image.png

  • e.g.:假设一个模型有N = 10^9(10亿个参数)，并且训练数据集的规模是D = 10^{12}(1万亿个tokens)。使用公式:C=6ND，总的计算量就是C = 6 x 10^9 x 10^12 = 6 x 10^21次FLOPs运算

  • 为什么系数是6：

    1. 前向传播：前向传播一次大约需要2FLOPs(一次乘法和一次加法)
    2. 反向传播：反向传播的计算开销是前向传播的两倍，因为需要计算梯度，涉及到额外的计算。反向传播大约需要4FLOPs
    3. 总FLOPs为前向传播+反向传播，为6FLOPs

  • 系数6是对Transformer模型的整体复杂度的一个近似，表明在进行一次训练时，模型的每个参数和每个token大约需要6次浮点数运算

Kaplan Scaling Law (OpenAI 2020)

image.png

Chinchilla Law (DeepMind 2022)

image.png

  • 如何通过将 C 分配给 N 和 D 来最大化模型性能：

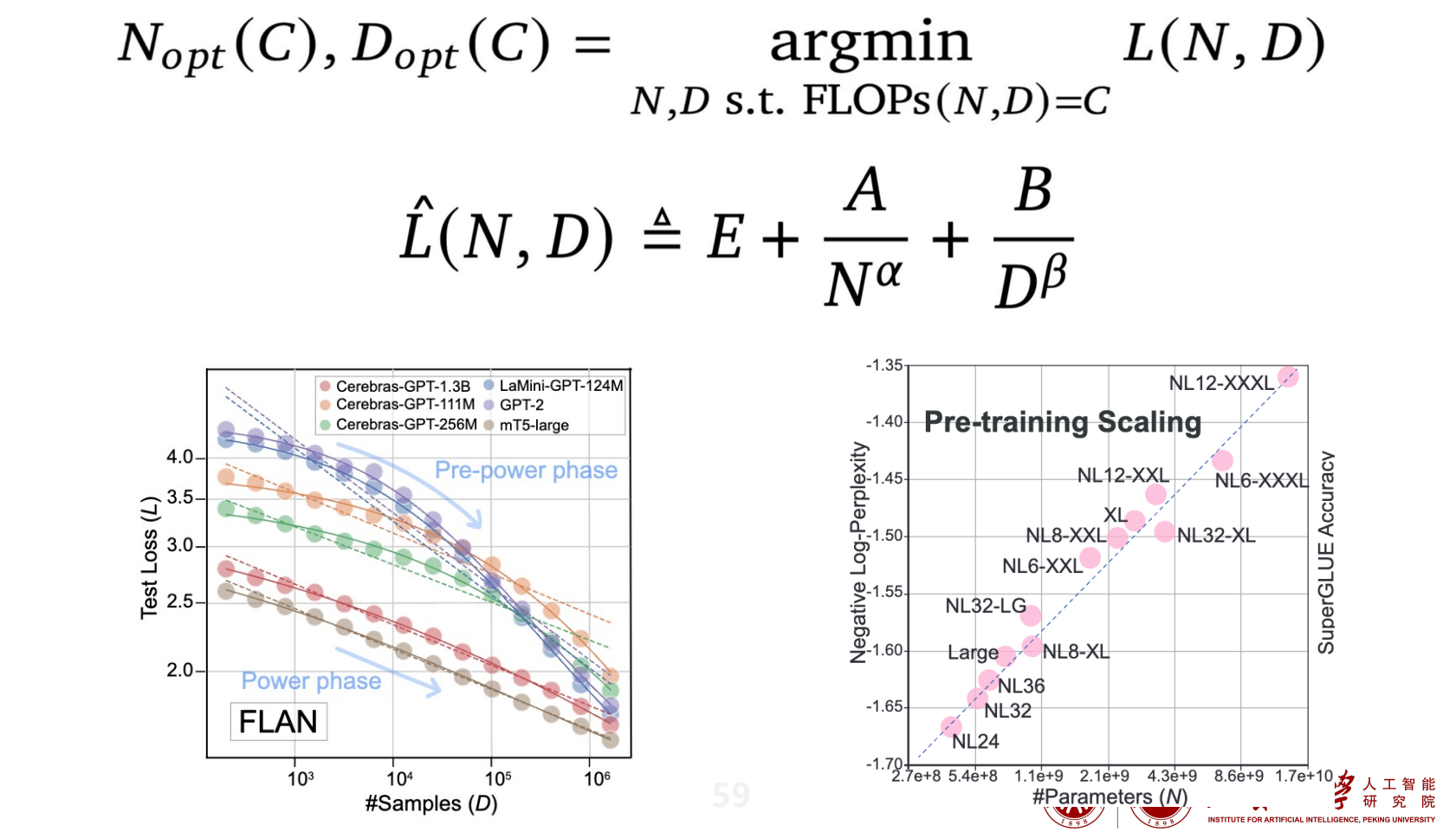
image.png

  • 对于用于训练 Gopher 的计算预算，最佳模型应该小 4 倍，同时使用 4 倍以上的标记进行训练。作者还表明，更大和高质量的数据集在进一步扩展语言模型方面发挥着关键作用，而不仅仅是增加参数的数量

Using the Scaling Law

  • 问题：如何通过将 C 分配给 N 和 D 来最大化模型性能？给定固定的 FLOPs 预算，应该如何权衡模型大小和训练tokens的数量？

  • Approach 1: Fix model sizes and vary number of training tokens 固定模型大小，改变训练数据

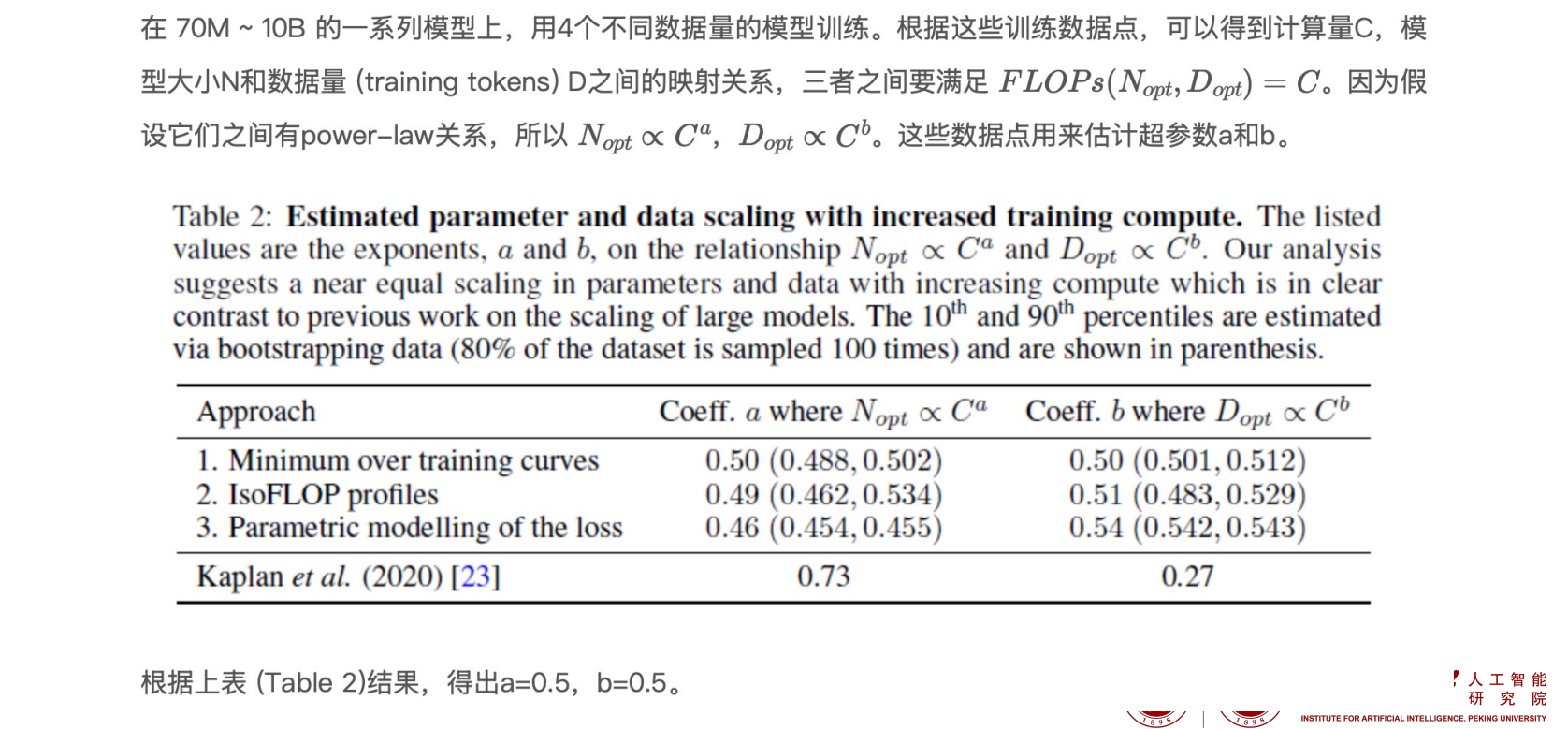
image.png

  • Approach 2: IsoFLOP profiles, the model size is varied for a fixed set of different training FLOP counts 固定计算量，改变模型大小

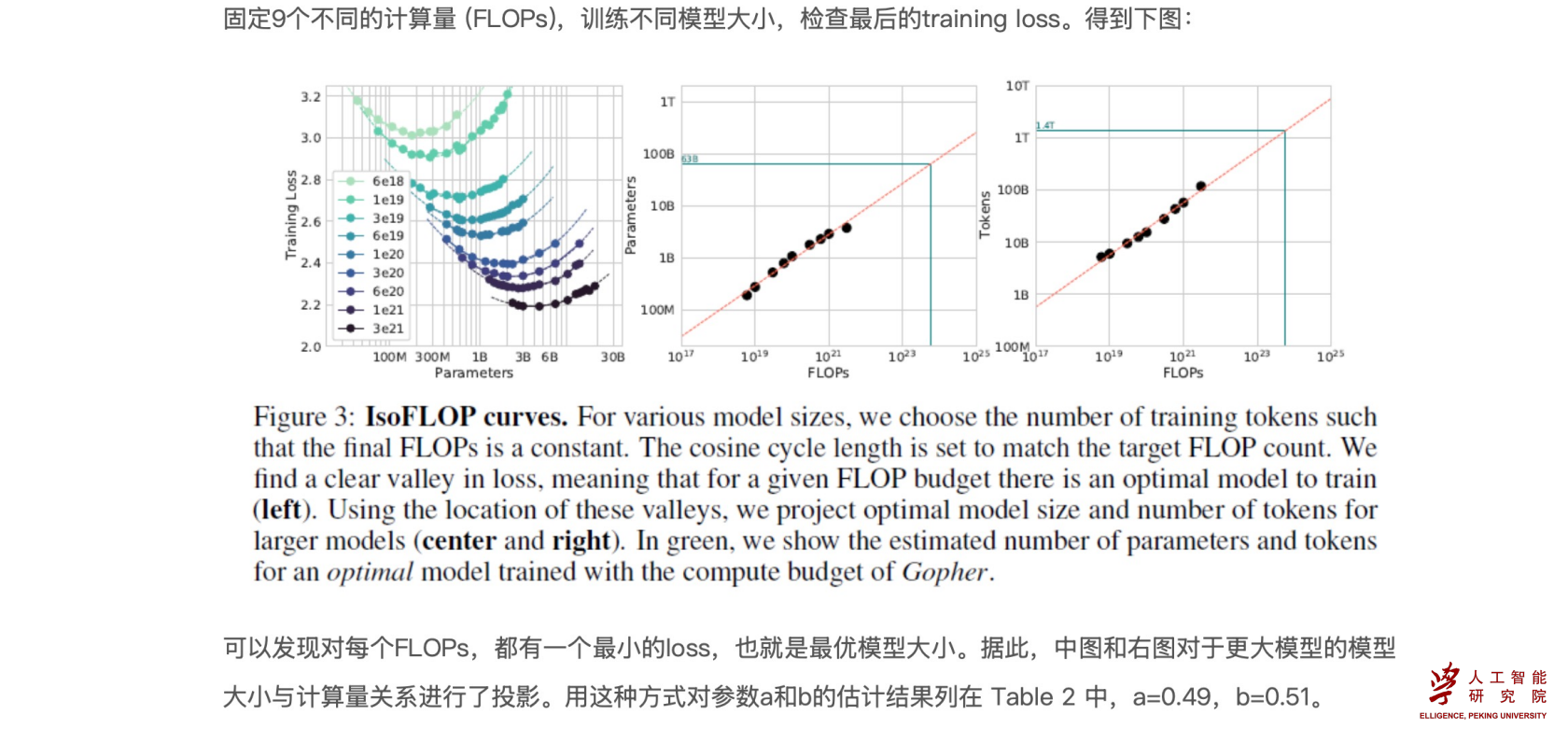
image.png

  • Approach 3: Fitting a parametric loss function 拟合幂律曲线

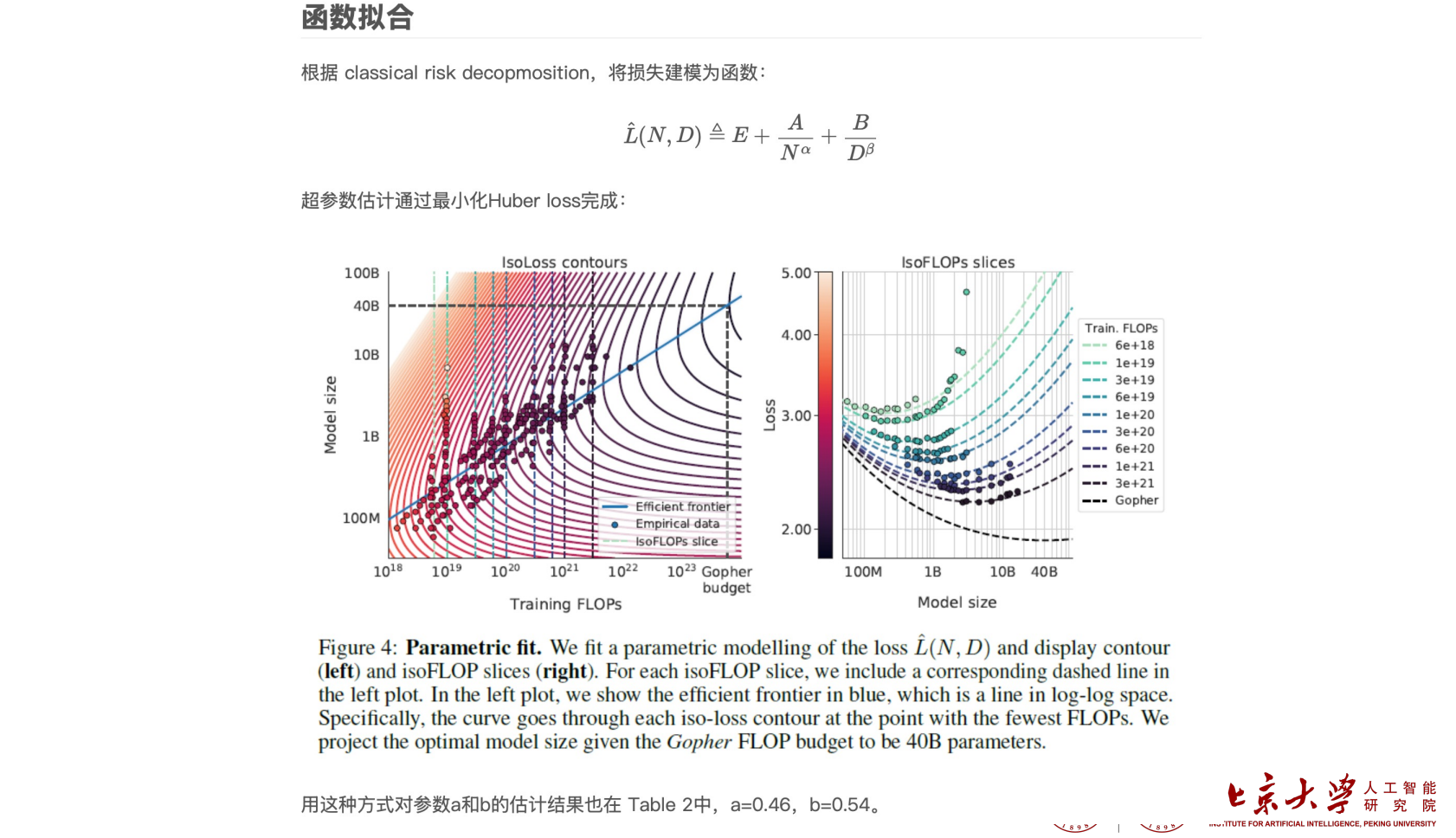
image.png

  • scaling law在实践中的应用：

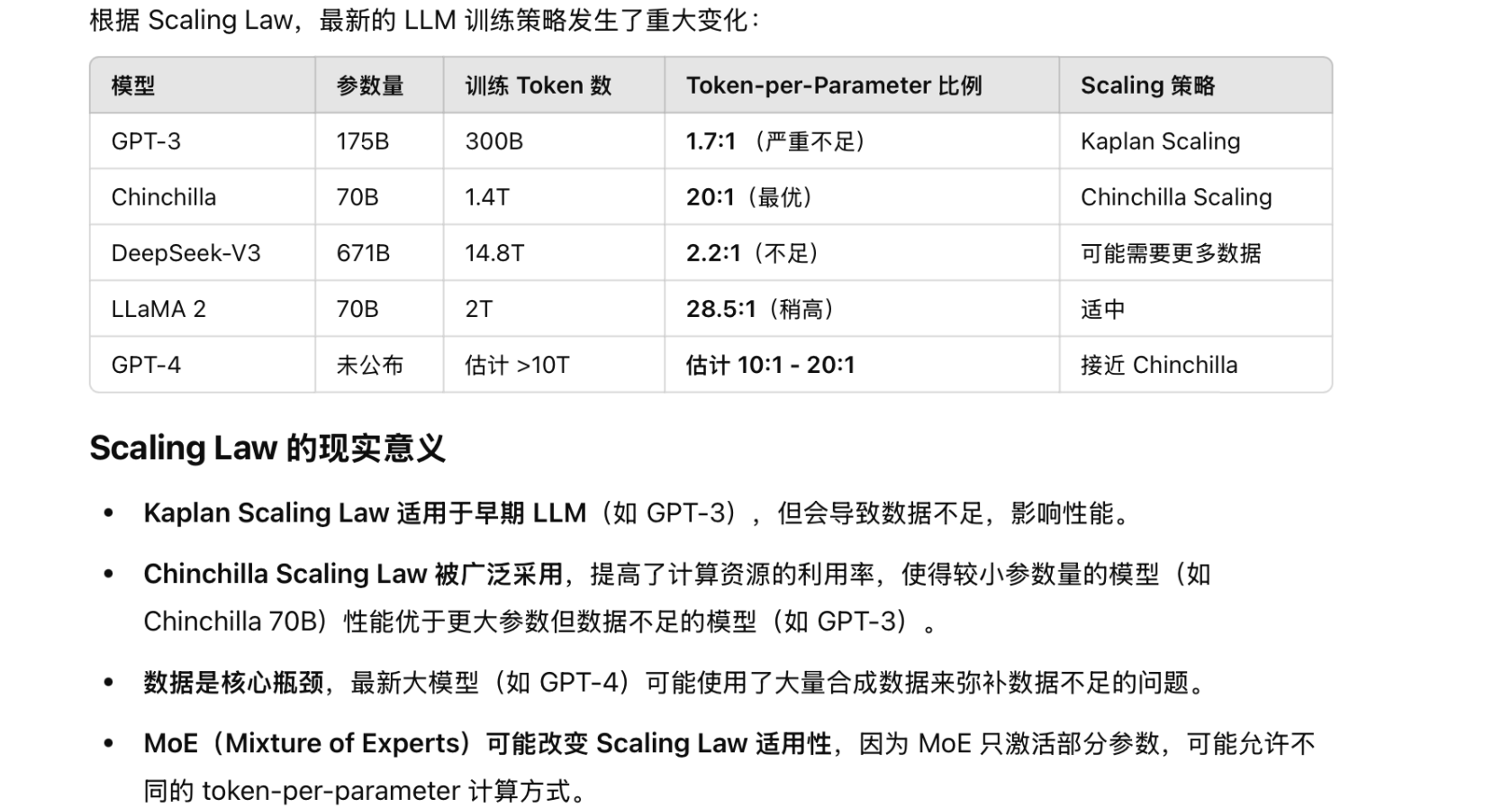
image.png

The Scaling Law in Llama 3.1

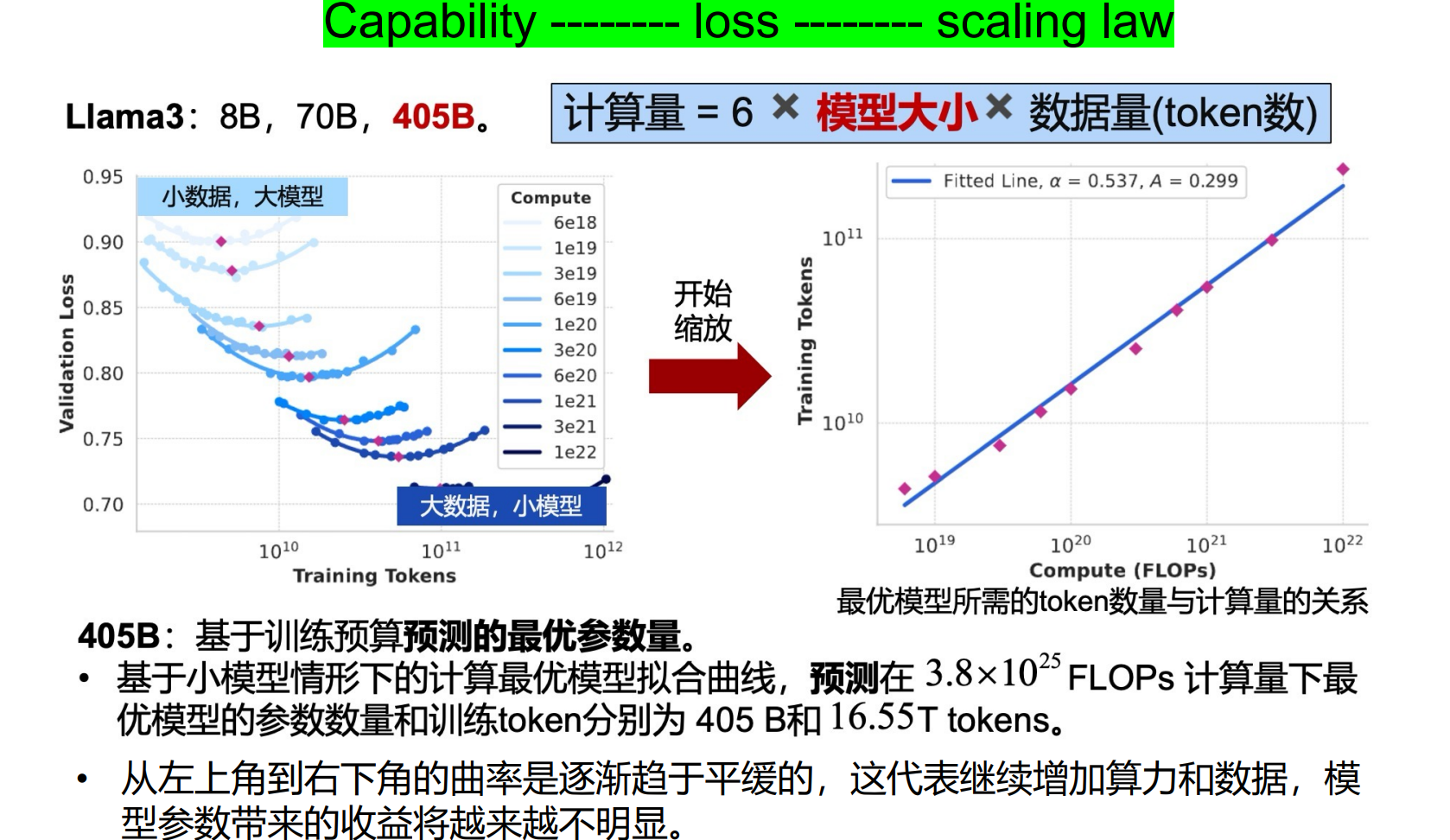
image.png

  • 当训练前损失小于 2.25 时，能力开始出现：CE 损失< 2.25 是能力涌现阶段的开始。这有助于预测性能：如果发现损失已经小于 2.25，则可以自信地使用幂律

  • 能力提高与损失相关

  • 具有相同预训练损失的不同模型在下游任务上产生相同的性能

Scaling Law in Summary

  • 总结：

    1. Kaplan Scaling Law（OpenAI，2020）：强调优先增加参数规模，但忽视了数据的影响，导致 GPT-3 训练数据不足
    2. Chinchilla Scaling Law（DeepMind，2022）：提出最优 token-per-parameter比例 ≈ 20:1，实现计算效率最大化
    3. 实践应用：GPT-4 及 LLaMA 3 可能采用了 Chinchilla Scaling Law，但 MoE 可能会影响 Scaling Law 的适用性
    4. 未来趋势：LLM可能依赖合成数据、MoE、优化计算方法 来突破数据和计算瓶颈

  • Scaling Law 未来研究方向：

    1. 数据极限问题：高质量公开数据已接近枯竭，未来可能依赖合成数据或人机协作数据生成
    2. 计算效率优化：未来的大模型可能会采用 MoE（专家混合）架构，只激活部分参数，以降低计算成本
    3. 新的 Scaling Law 公式：可能需要针对混合精度训练（FP8）、自监督学习、对比学习等新方法 重新拟合 Scaling Law

  • scaling law如何对大模型的性能进行预测和监控：

    1. 可预测性：缩放定律显示，模型在增大参数、数据和计算量时，损失（如交叉熵）会呈现幂律下降的趋势。这使得我们能够通过小模型的表现来预估更大模型的性能，并用于调试和监控训练过程
    2. 边际收益递减：尽管扩大模型规模会不断带来性能提升，但提升的速度会逐渐减缓，即存在“收益递减”现象
    3. 任务级别预测难题：尽管语言建模损失可以平滑下降，但这种改善不一定能直接转化为下游任务的性能提升，有时甚至可能出现“反向缩放”现象，即损失下降反而伴随特定任务性能的下降

  • 大模型中出现的“涌现能力”——即小模型中不存在而在大模型中突然出现的能
    力

  • 定义：涌现能力是指只有当模型规模超过某一临界值后才会显现出来的特定能力，如在上下文学习（in-context learning）、指令遵循和链式思考（chain-of-thought）等能力

  • 现象描述：这些能力往往表现为在模型达到一定规模后，性能会突然大幅超出随机水平或传统方法的表现，类似于物理中的相变现象

  • 任务依赖性：涌现能力通常与任务复杂性密切相关，不同任务可能需要不同的临界规模才能激发出这些能力

  • scaling law与涌现能力之间的关系：

    1. 两种视角的互补性：缩放定律反映了模型性能（通常以语言建模损失为度量）的平滑、可预测的改进趋势；而涌现能力则展示了模型在达到某个规模后，在特定任务上会出现突飞猛进的性能跃升
    2. 临界现象：虽然整体性能随着规模的增加逐步提升，但某些复杂任务的能力只在模型达到临界规模后才突然“开窍”，这表明涌现能力与单纯的平滑缩放并不完全对齐
    3. 评估和研究挑战：如何将语言模型的整体损失改善与具体任务表现之间的关系精确对应起来，还存在争议和挑战。部分研究者认为，涌现现象可能与评估指标设置有关，而另一些则认为它是大模型内在机理的真实反映

The Scaling Law in RL

  • 重新定义Reward，引入Intrinsic Performance:

    1. 在不同规模的同家族模型上实现当前策略回报所需最小计算量
    2. 哭花了在模型size和环境interactions两个维度上的幂律关系

  • 关键发现：

    1. 任务性能、模型大小和环境交互数量之间的关系
    2. 在给定计算量下的最佳模型大小遵循幂律关系
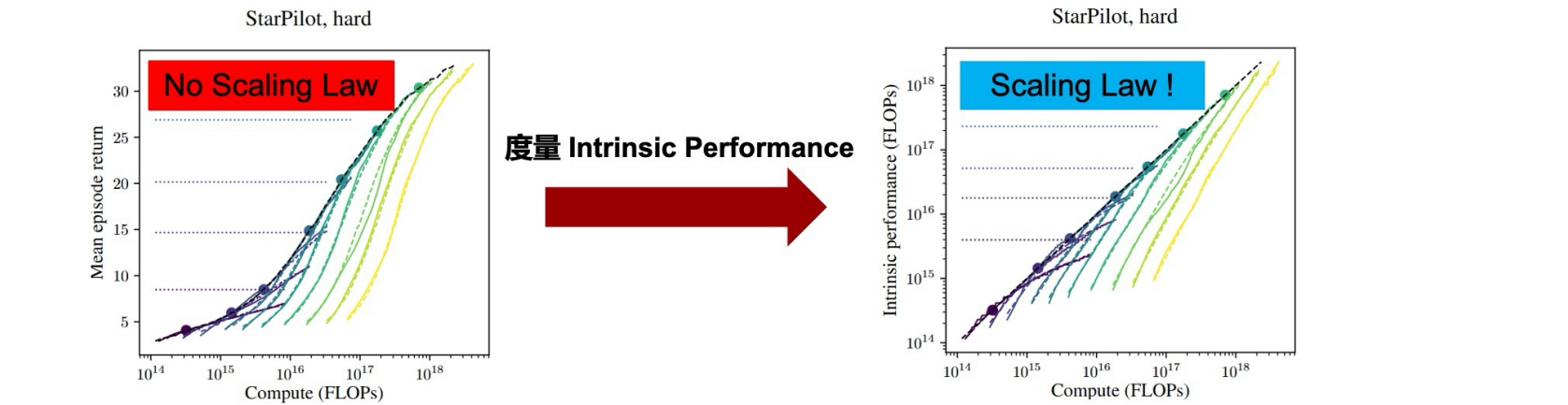
      image.png

image.png

  • 核心洞见：
    1. RL的Scaling laws在不同环境上得到了验证，与语言模型展现了相同的轨迹
    2. 环境的交互时间变长，任务horizon变大，不会改变缩放关系

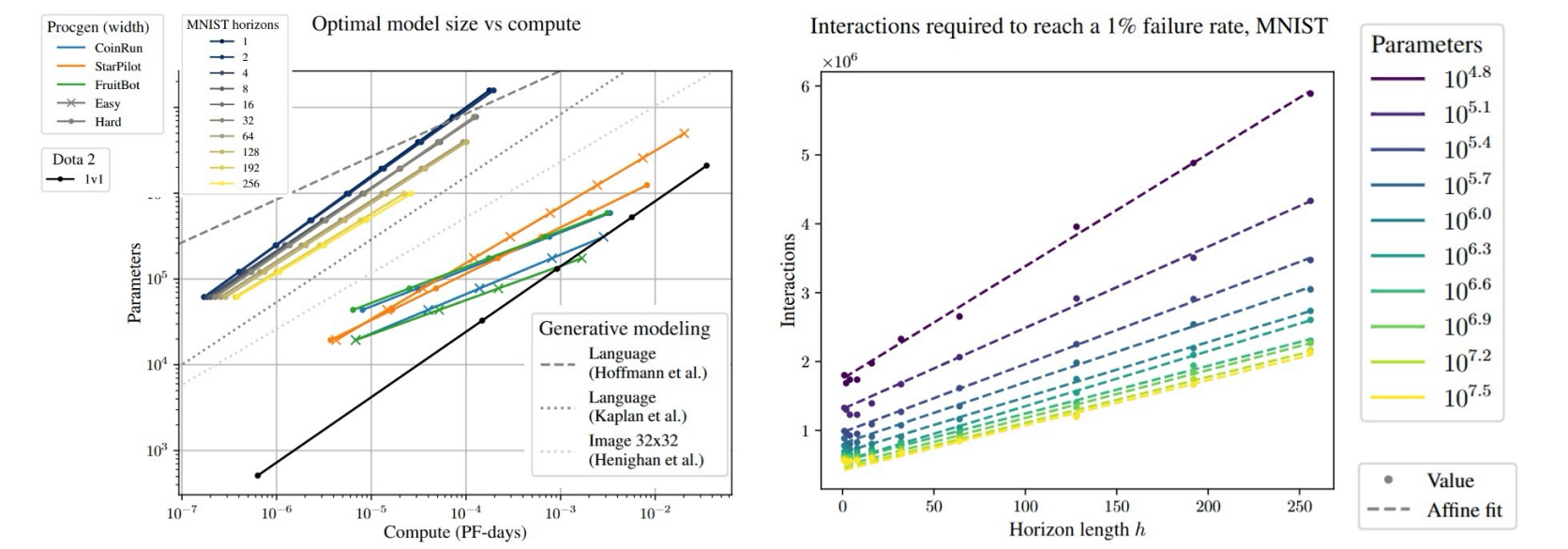
image.png

Post-Training Scaling Laws

  • 随着模型尺寸逐渐增大，预训练阶段参数 Scaling Up 带来的边际收益开始递减；如果想要深度提升模型推理能力和长程问题能力，基于RL的 Post-Training 将会成为下一个突破点

  • 自回归模型在数学推理问题上很难进步的一点在于没有办法进行回答的自主修正，如果仅是依靠生成式方法和扩大参数规模，那么在数学推理任务上带来的收益不会太大。所以需要寻找额外的 Scaling Laws

CoT

system1&2

  • system1是快速，直觉的思维：

    1. 特点：自动化、无意识、直觉式的思维模式，依赖于习惯和本能
    2. 速度：非常快，瞬间反应
    3. 准确性：通常有效，但是可能产生偏差和错误，特别是复杂情况下
    4. 典型应用：处理简单任务，如人脸识别、驾驶熟悉的路线
    5. 优点：节省认知资源，可以在大多数情况下做出快速有效的决策
    6. 缺点：容易受到认知偏差和情绪的影响，面对复杂问题可能出错

  • system2是慢速，分析的思维：

    1. 特点：有意识，深思熟虑的思维模式。依赖于逻辑推理和分析，需要更多的认知资源和时间
    2. 速度：较慢，涉及到深入的思考和计算
    3. 准确性：更加精确，尤其是需要处理复杂抽象的问题
    4. 典型应用：解决数学问题，规划未来，做出权衡和推理
    5. 优点：可以在复杂的情景下做出更为理性和精确的决策
    6. 缺点：消耗大量的认知资源，可能会导致疲劳和效率较低

Chain-of-Thought

  • 需要在 Instruction Following Agent 中进行推理，因为system1和2明显是两种完全不同的思维模式 -> CoT

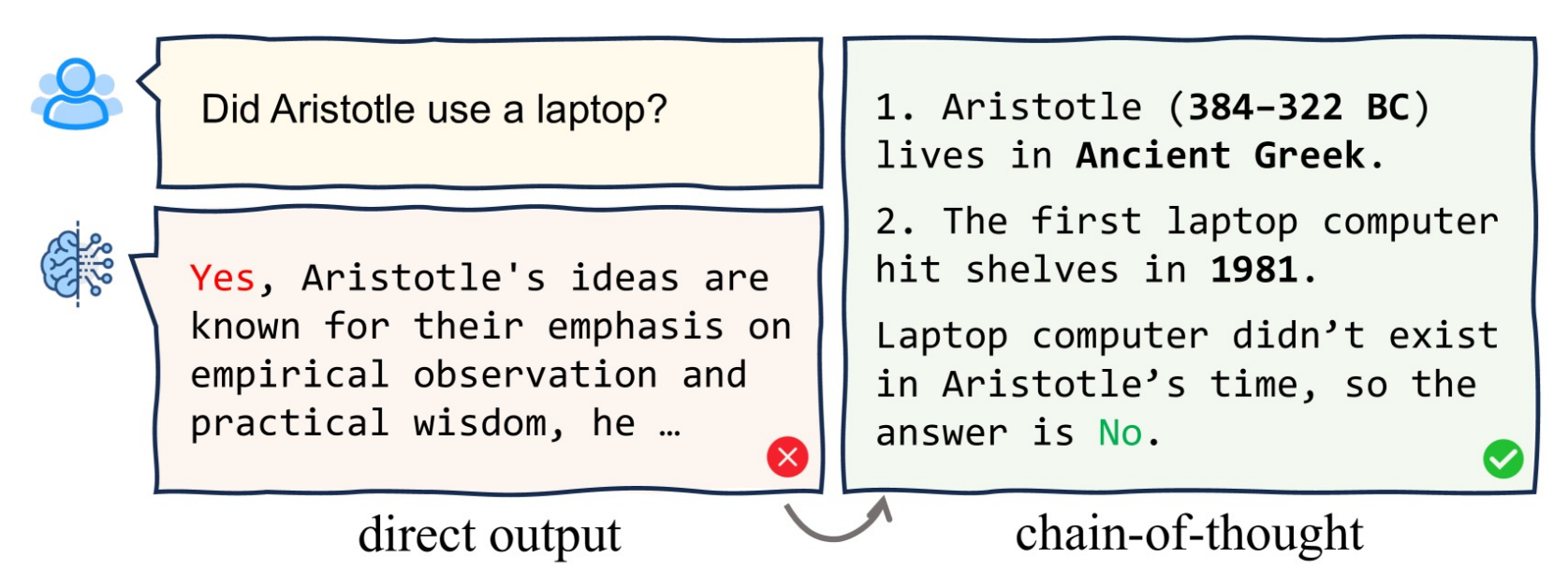
image.png

o1的技术范式改变

  • OpenAI o1 的训练：Q* \ Tree Search

  • 启发行业在模型规模达到一定量级后，更多的将算力投入到Post-Training 阶段的 RL 训练和推理阶段模型的思考过程当中

image.png

  • OpenAI o1 运用的技术关键还是在于RL的搜索与学习机制：

    1. 基于 LLM 已有的推理能力，迭代式的 Bootstrap 模型产生合理推理过程(Rationales) 的能力
    2. 并将 Rationales 融入到训练过程内，让模型学会进行推理
    3. 而后再运用足够强大的计算量实现 Post-Training 阶段的Scaling。类似于 STaR [1] 的扩展版本

  • 后训练扩展律 Post-Training Scaling Laws 已经出现

  • 模型学习的是产生合理推理的过程，MCTS 在其中的作用是诱导合理推理过程的产生或构建相应的偏序对形成细粒度奖励信号

  • 模型的 Bootstrap 有助于构建新的高质量数据，并且新的Rationales 数据促进了模型进一步提升能力

Post-Training Scaling Laws

  • Post-Training 阶段，随着训练时计算量（来自RL的Training阶段）和 Test-Time 计算量（例如Test-Time Search）的增长，模型性能（例如数学推理能力）也会随之提升

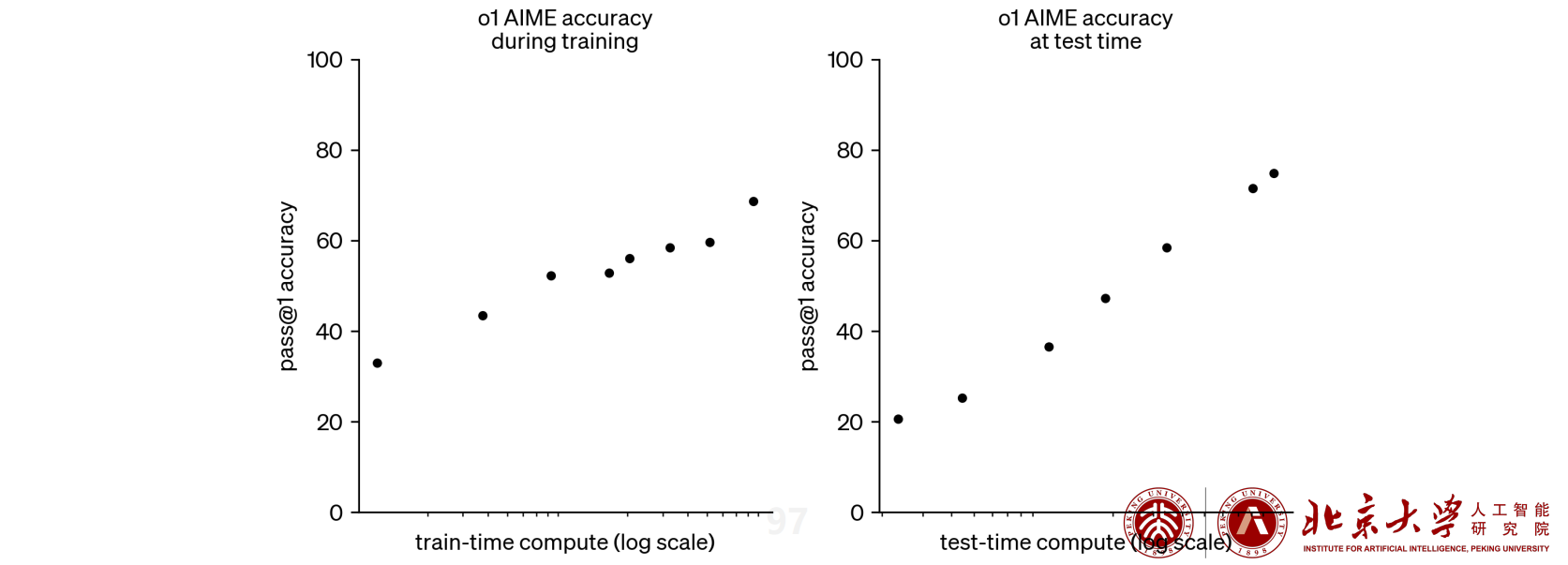
image.png

OpenAI o1 技术路径推演

  • 生成过程中的 Reasoning Token 是动态引入的，这也尽可能的减少了不必要的思考带来的额外算力损耗

  • RL + “隐式思维链”：o1 模型使用 RL 进行训练，通过引入动态的 Reasoning Token启发 “隐式思维链” 来 “思考” 问题，思考时间越长，推理能力越强

  • 快思考 -> 慢思考：可以说，OpenAI o1 已不再是即时给出答案的模型，而是能够先进行深入思考。这可以类比为 o1 正在从依赖系统 1 思维（即快速、自动、直觉、易出错的思维模式），逐步进化为采用系统 2 思维（即缓慢、刻意、有意识且更可靠的推理过程）

  • 推理时间 = 新的扩展维度：o1 模型的发布，意味着 AI 能力的提升不再局限于预训练阶段，还可以通过在 Post-Training 阶段中提升 RL 训练的探索时间和增加模型推理思考时间来实现性能提升，即 Post-Training Scaling Laws

  • 数据飞轮 + Bootstrap -> SuperIntelligence : 基于自我反思的模型将能够实现自举 Bootstrap，并提升大大提升模型对于未见过的复杂问题的解决能力，模型的推理过程形成大量高质量数据的飞轮，并最终有可能向 SuperIntelligence 更进一步