计算机视觉 03 Image Processing
Image Processing
An Image as a 2D Function:可以是离散,也可以作为2维(黑白)、3维(彩色)函数
图像:
- Range: 𝐼 𝑥, 𝑦 ∈ 0, 255 ∈ ℤ
- Domain: 𝑥, 𝑦 ∈ 1, 𝑤𝑖𝑑𝑡ℎ , 1, ℎ𝑒𝑖𝑔ℎ𝑡
- Color Image: 𝐼(𝑥, 𝑦, 𝑐)
Pixel (Point) Processing

- Darkening v.s. Contrast
- 明暗:所有像素变量或变暗,相对差异保持不变(通过+、-)
- 对比度:相对差异改变(*、/)

Histogram Equalization(直方图均衡化)
调成均匀分布则图像会更均匀
具体操作:对直方图压缩y轴至0-1,找出概率分布,再根据概率分布将y轴拉长至0-250。
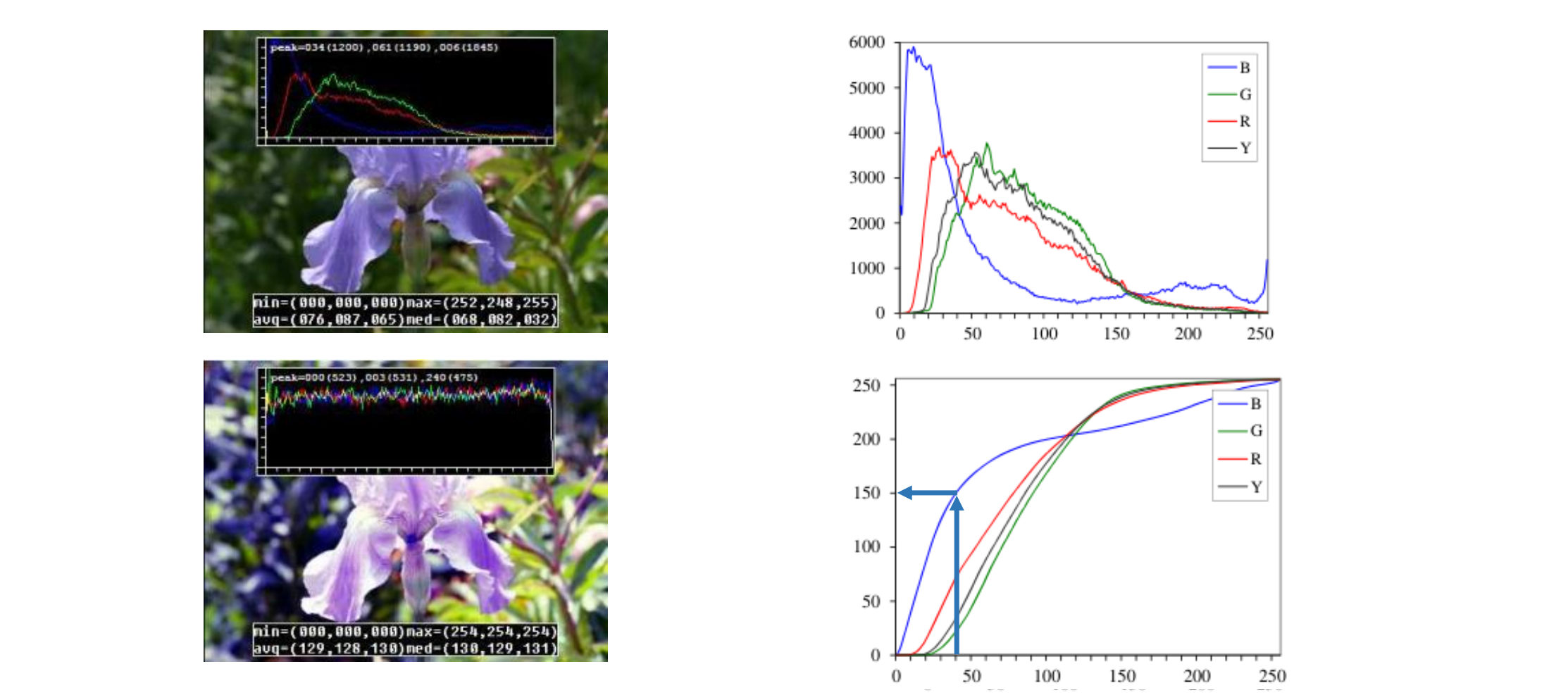
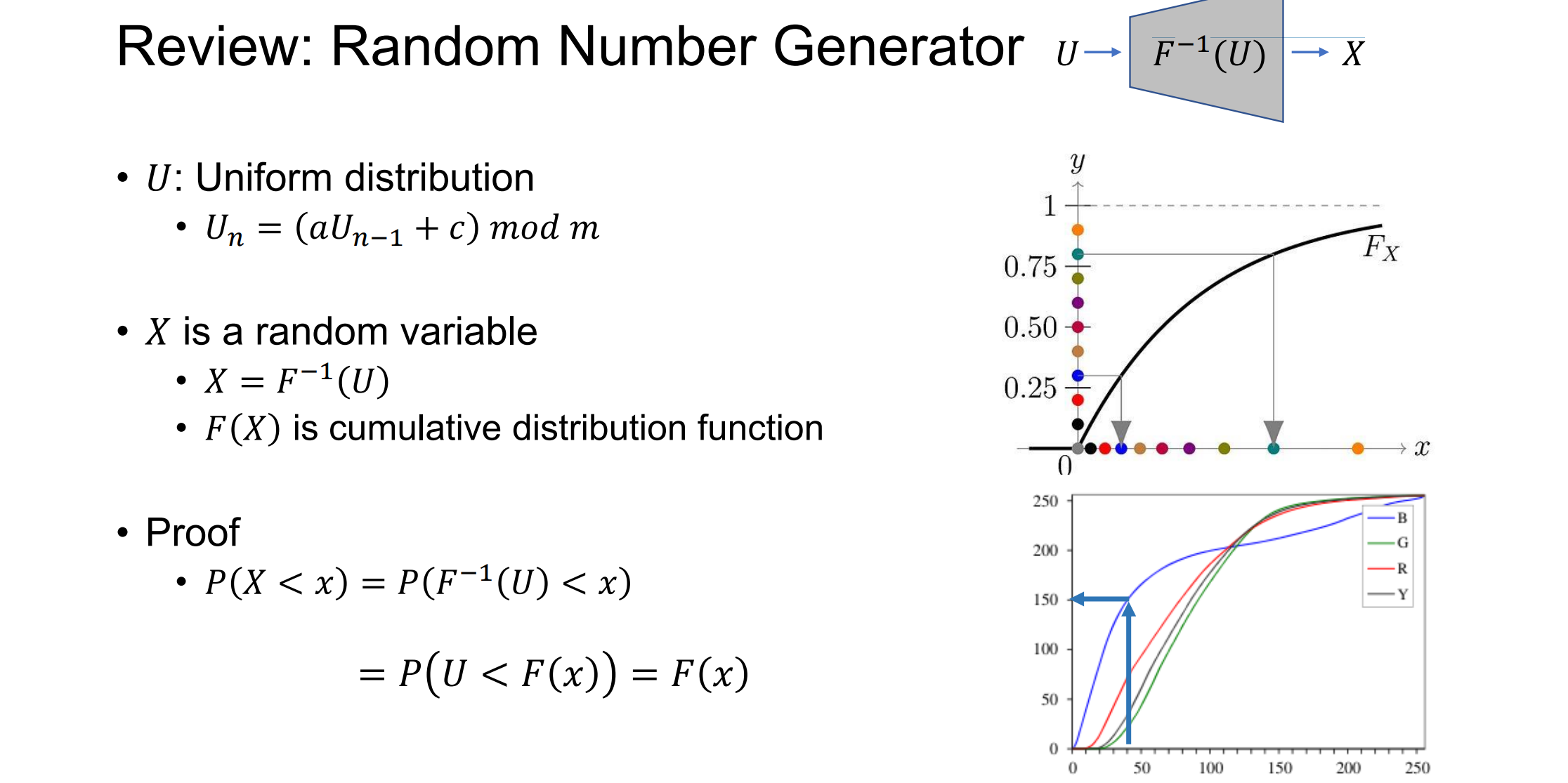
Image Filtering
- Image Filtering用于图像邻域处理
Linear Filters
𝐼 𝑖,𝑗 : 𝑤 × ℎ digital image;ℎ 𝑢, 𝑣 : 𝑚 × 𝑛 “filter” or “kernel”
输出图像中的每个像素都是原始图像中对应输入像素及其相邻像素的线性组合:以i,j为中心,在邻域选取图像块,再与filter相乘
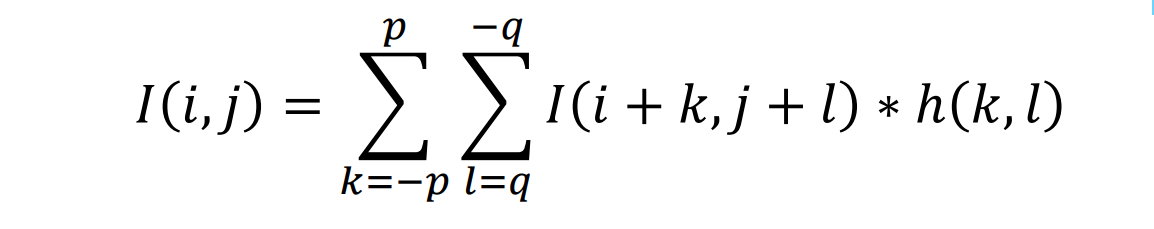
Boundary Effects的处理:
- 忽略边界:会导致image变小
- 补0填充:Pad zeroswhen a value is required at positionsoutside the image range
- 周期性假设:顶行环绕到底行;最左边的列换行到最右边的列
- 反射边界
torch.nn.functional.pad(image, pad, mode=’constant’, value=None). mode – ‘constant’, ‘reflect’, ‘replicate’ or ‘circular’
几种主要的Linear Filters:
- shift left by 1 pixel:左移把1放到最右边中间
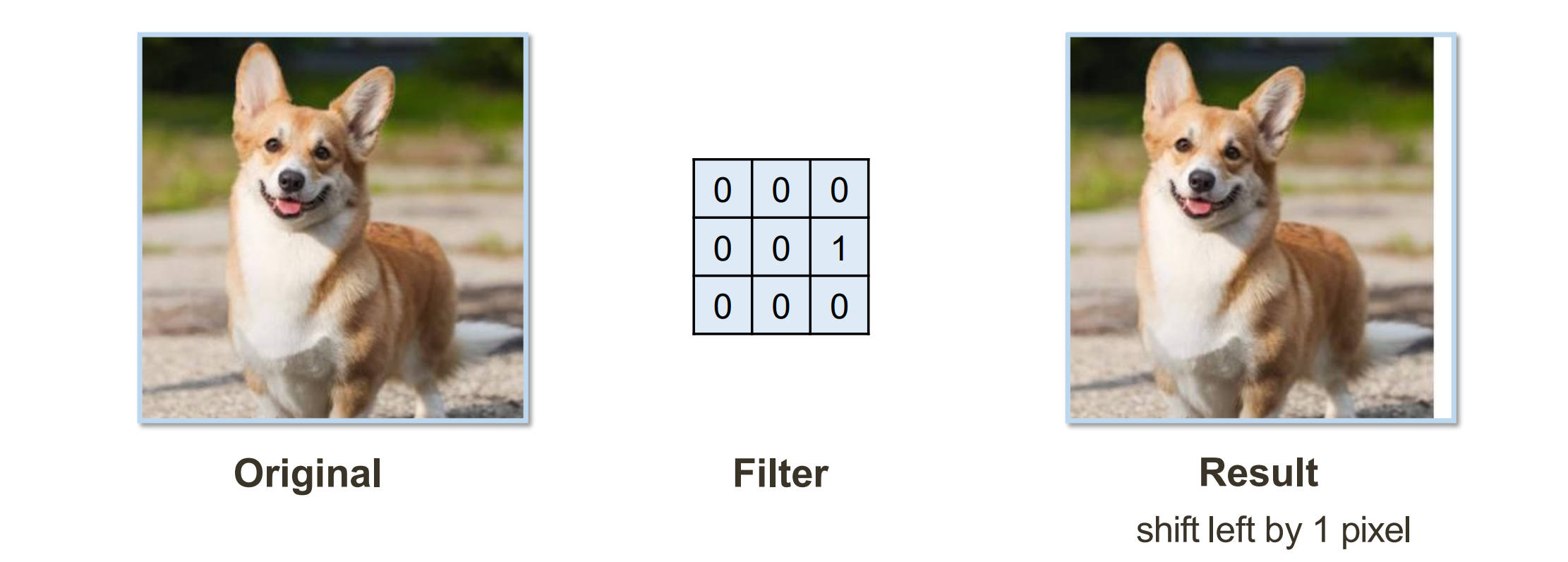
- Box Filter:加权平均,模糊化处理
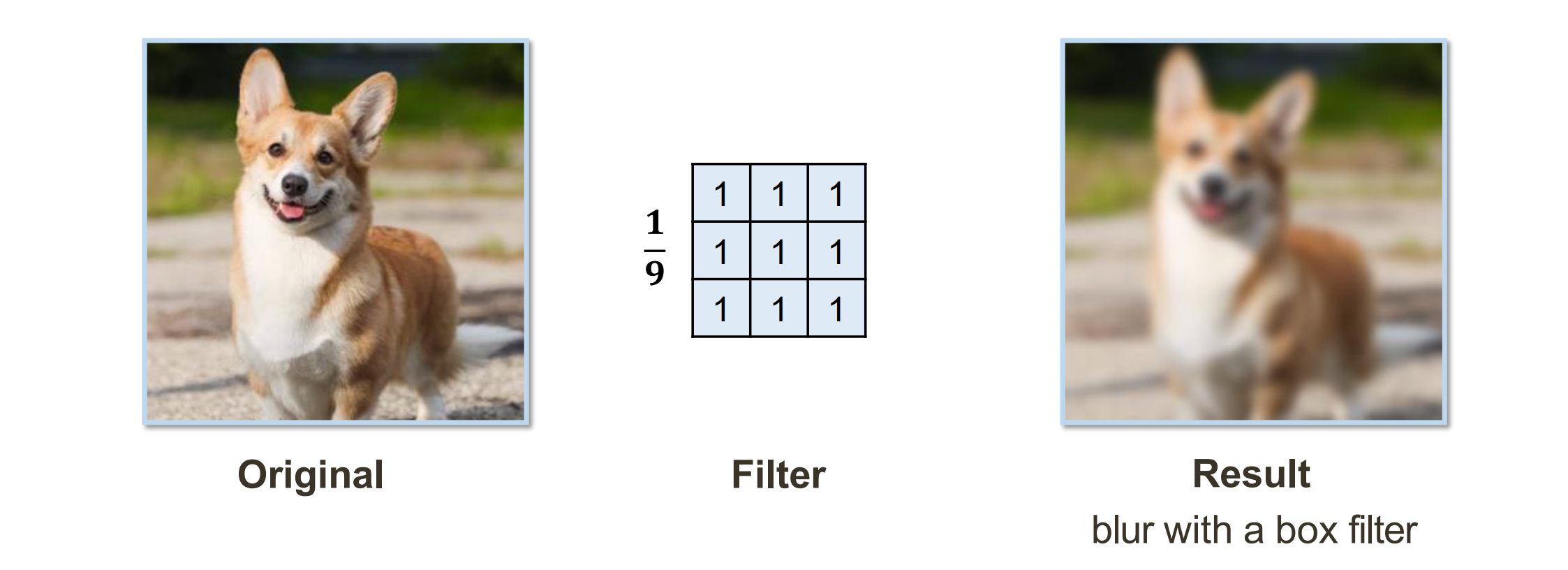
- Gaussion Filter – Low Pass Filtering:低通滤波,按距离归一化处理,否则明暗会发生变化
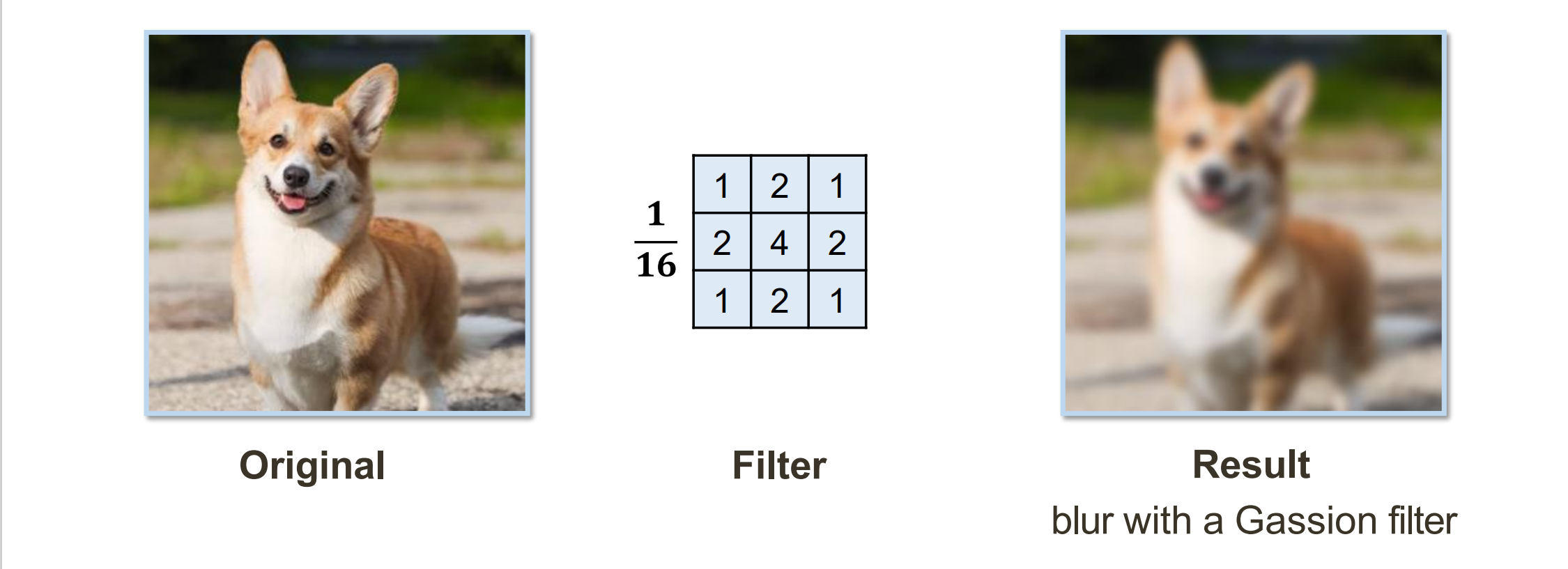
- Sharpening Filter:锐化
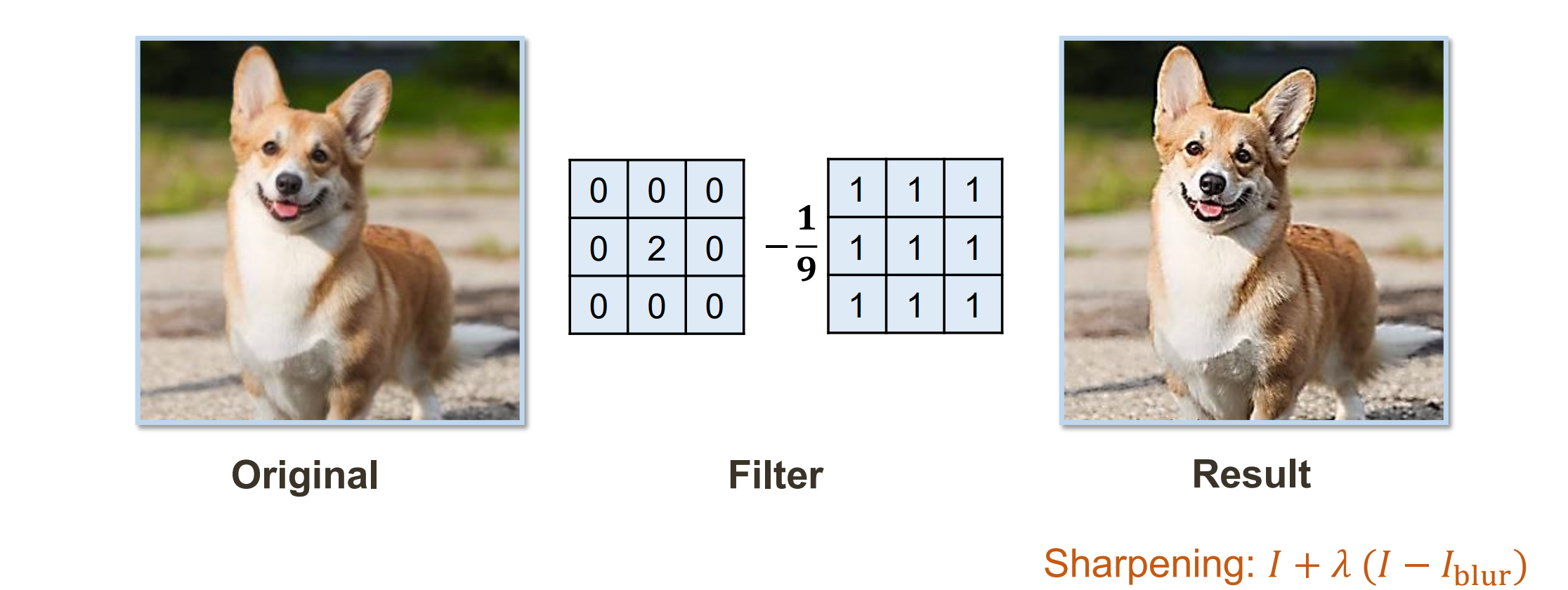
- shift left by 1 pixel:左移把1放到最右边中间
图像筛选需要每个像素进行 K ^ 2(乘法和加法)运算。首先执行 1D 水平过滤,然后执行 1D 垂直过滤,这需要每个像素总共 2K 次操作,从而加快速度
2D 内核 H 对应于水平内核 h 和垂直内核 v 的外积 : K = v x h.T 。对于内核 K,取其奇异值分解 H = ∑(i)σiuivi
Properties of Liner Filtering(线性滤波的性质)
- 齐次性、可加性、平移不变性、运算符可叠加
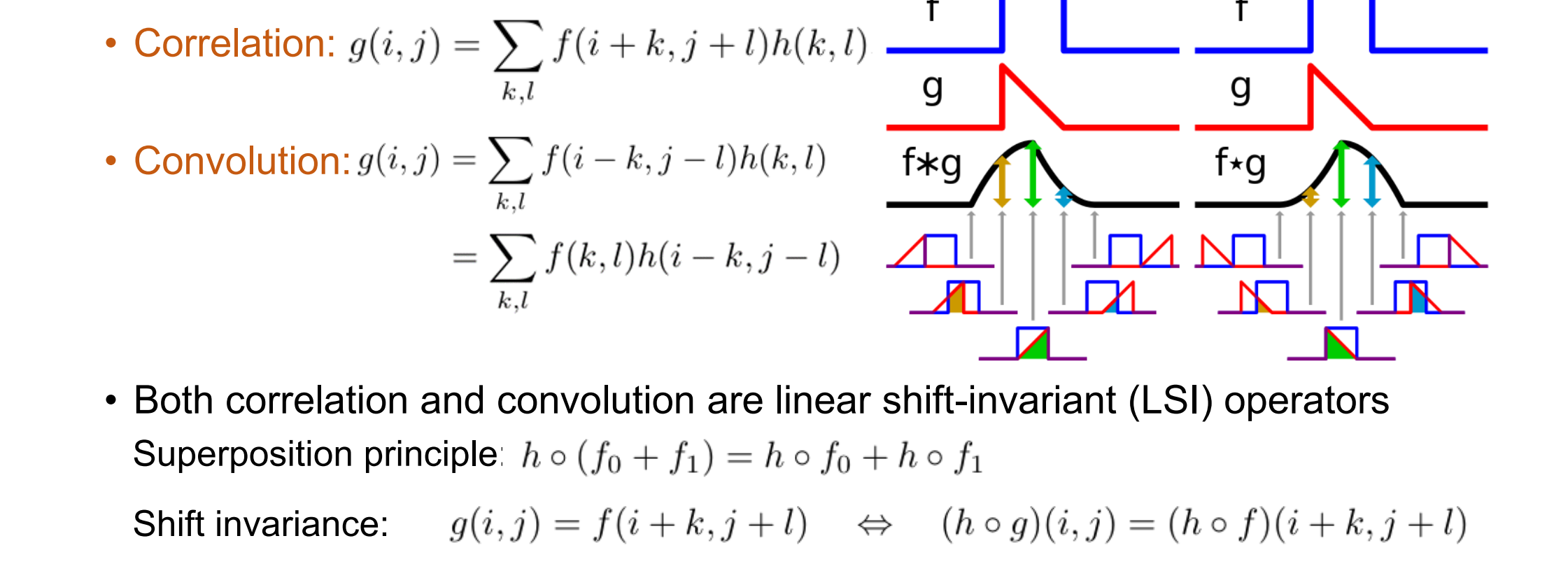
- 可应用于卷积神经网络
- 滤波可写成矩阵x向量的形式:g = Hf
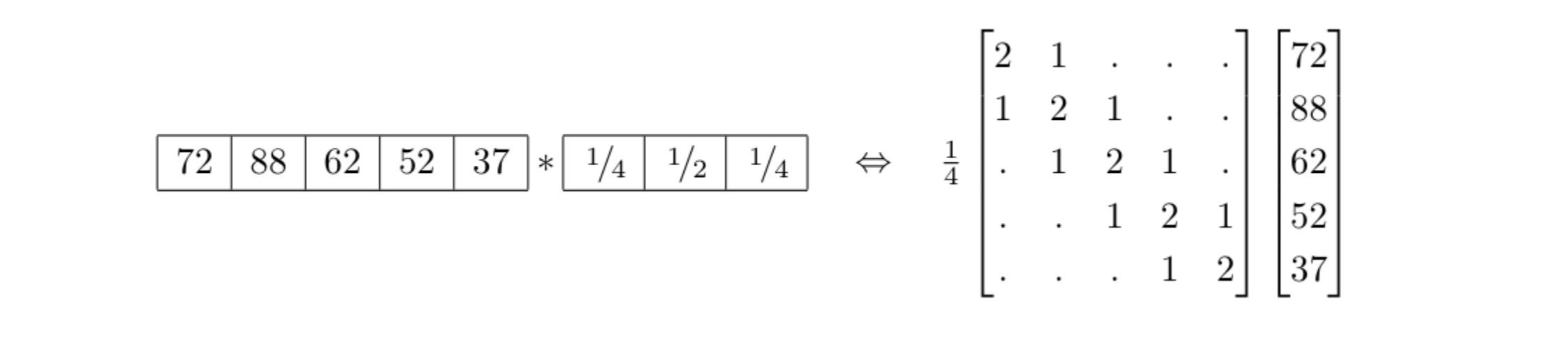
- 齐次性、可加性、平移不变性、运算符可叠加
Non-Linear Filtering
Gaussian Filter Revisited(审视): ‘Salt and Pepper’ Noise(椒盐噪音)
- 椒盐噪音:

- 可以通过中值滤波(Median Filter)来消除椒盐噪音的影响:对一个区域的像素进行排序,选择其最中间值作为滤波的输出值
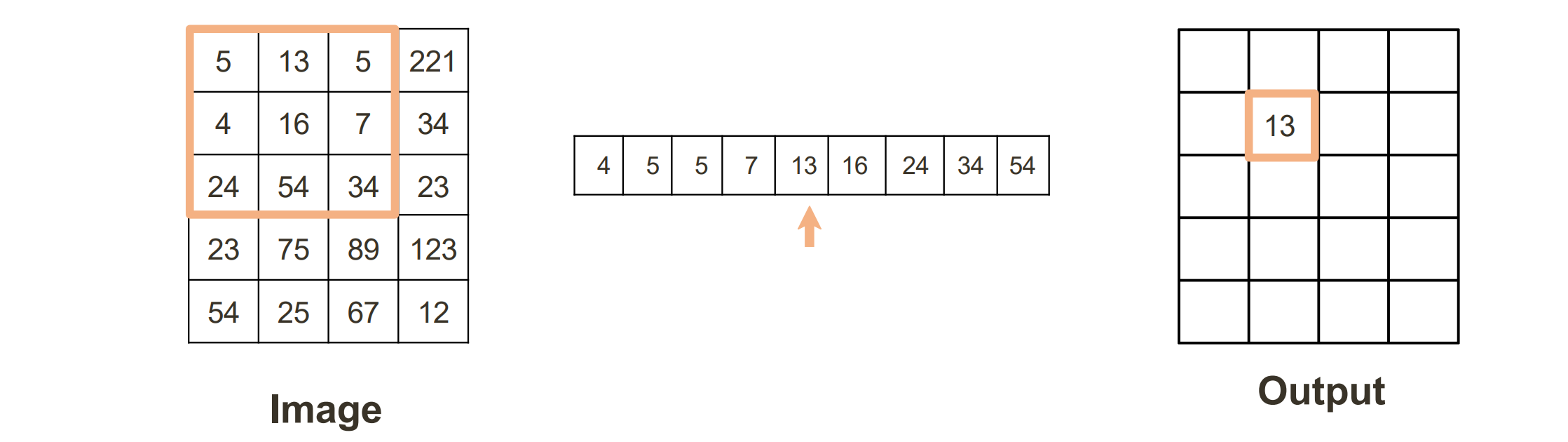
- 中值滤波器强制具有不同值的点更像其相邻点
Gaussian Filter Revisited: Sharp Edges
- 双边滤波(Bilateral Filter):可以解决模糊不清的问题

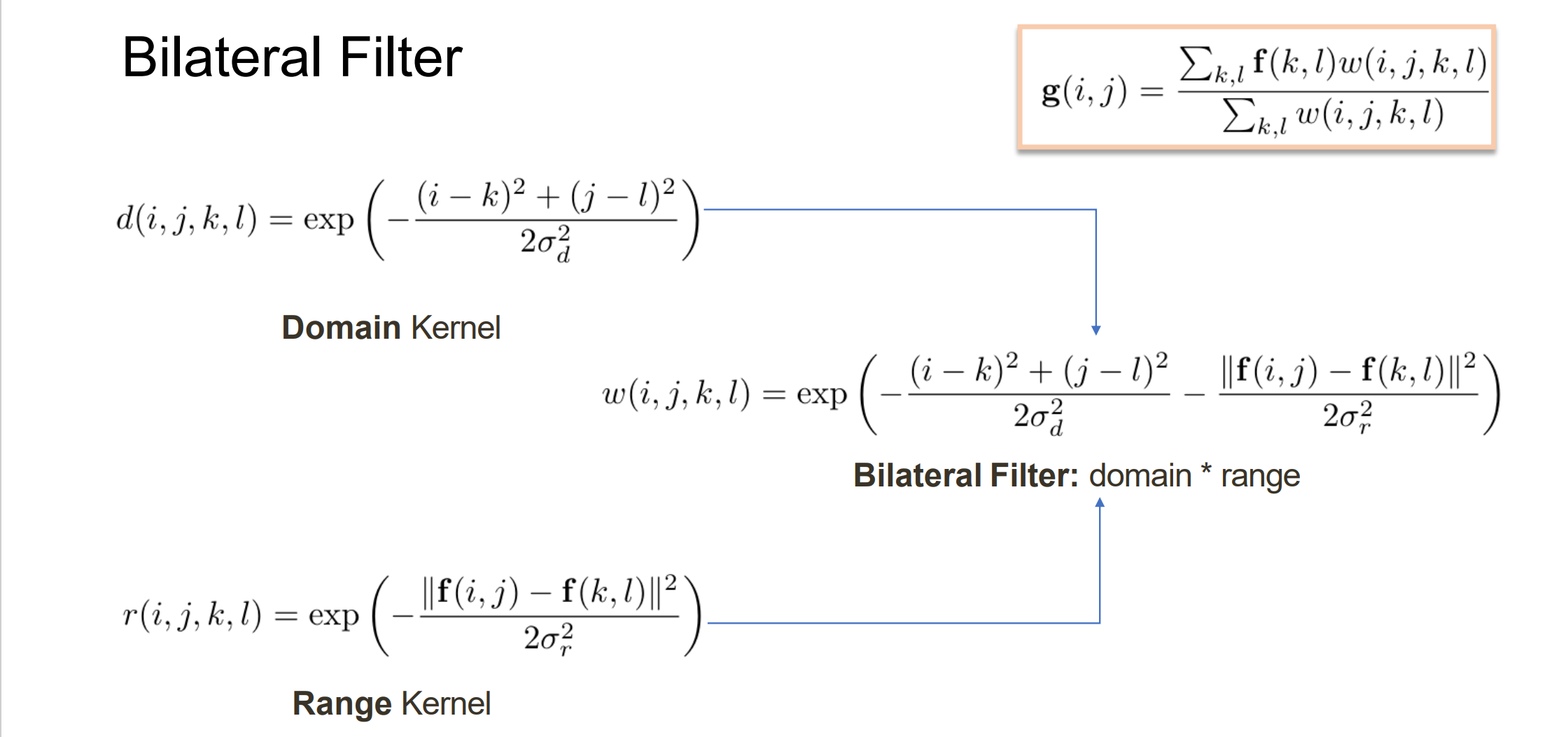

Applications of Image filters
Correlation: Template Matching(局部检测)
- Locate the template in the image
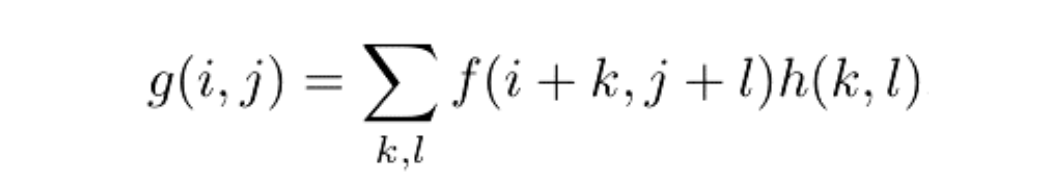
其中f代表图像、h代表滤波
Normalized Correlation
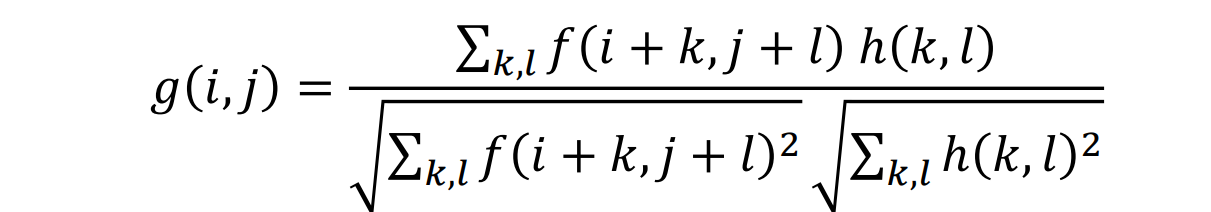
- 归一化解决了像素颜色的影响,而使得检测只取决于局部的形状
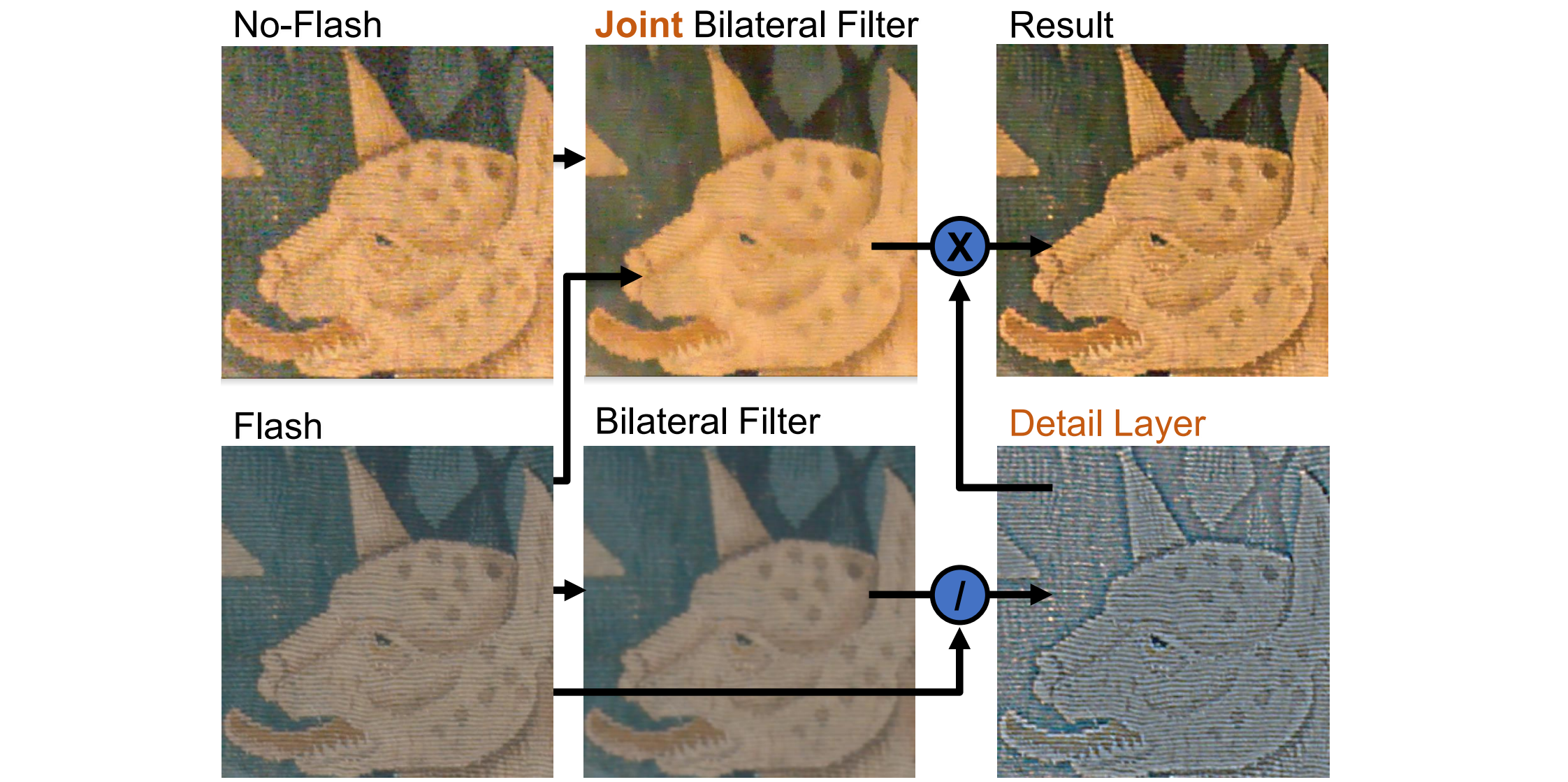
Bilateral Filter: Photography with Flash / No-Flash Pair
Flash / No-Flash Pair:
- Flash: Low Noise,Sharp,Artificial Light,Jarring Look(外观不和谐)
- No-Flash:High Noise,Lacks Detail,Ambient Light(环境光),Natural Look
图像(函数)解释:Large 𝜎𝑟 → over blur;Small 𝜎𝑟 → can’t remove noise
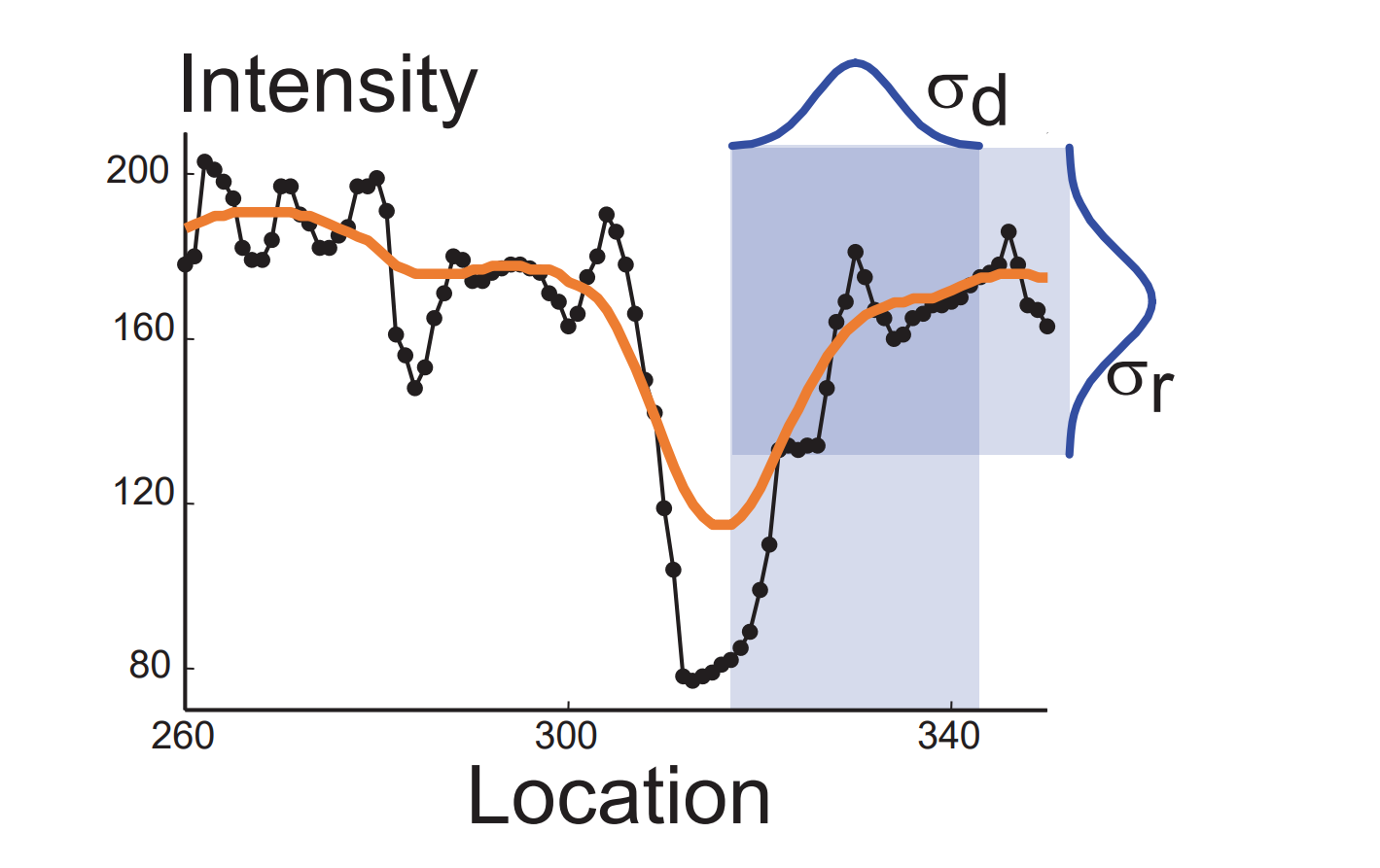
A value in-between can smooth the signal and preserves some edges, but it’s not perfect
Joint Bilateral Filter:思想:用无噪音的图像(Flash)指导颜色。用保真的图片(Flash)衡量相似性
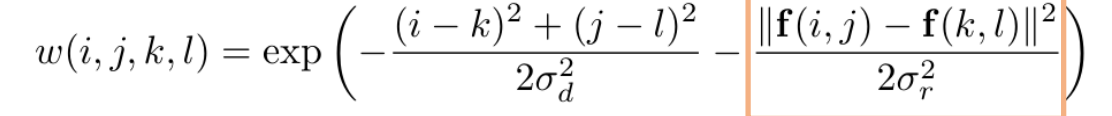
Upsampling / Downsampling Pyramids
Image Downsampling / Subsampling:generatea smaller image from a big image
降采样方法:Throw away every other row and column to create a 1/2 size image
Image Subsampling: Aliasing
产生原因:当采样率不够高,无法捕捉图像中的细节量时,就会出现走样。降采样会放大噪音
反走样方法:应该首先过滤掉图像中的高频细节。高斯滤波器可以平滑高频细节,又名低通滤波器
Subsampling with Gaussian Pre-filtering
方法:先进性高斯滤波再进行降采样丢弃行列的像素
模糊 -> 降采样 -> 模糊 -> 降采样…重复此过程形成高斯金字塔
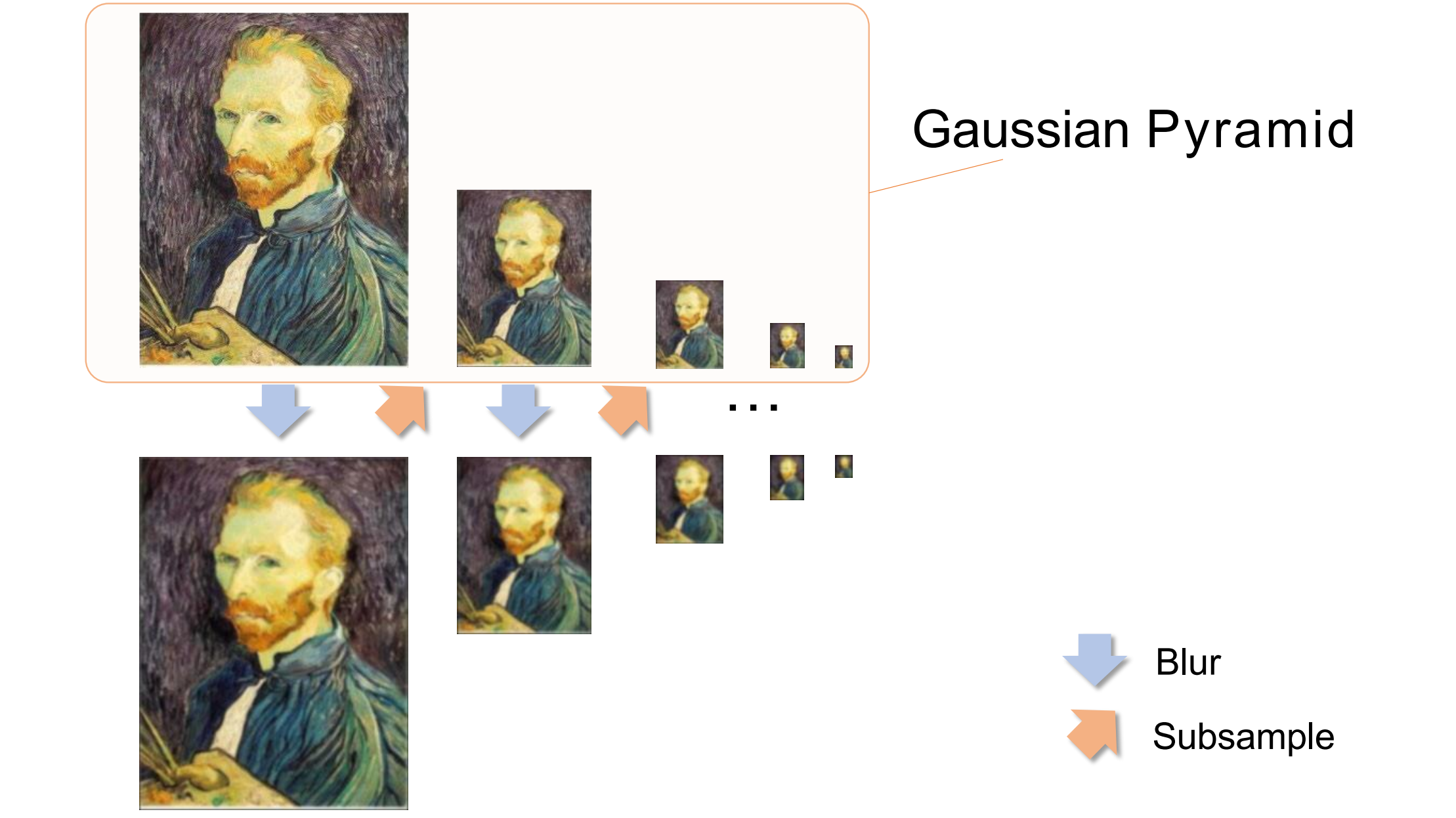
Image Upsampling(上采样)
初级方法:最近邻插值(nearest neighbor interpolation):repeat each row
and column 10 times最近邻插值的局限性:不够平滑
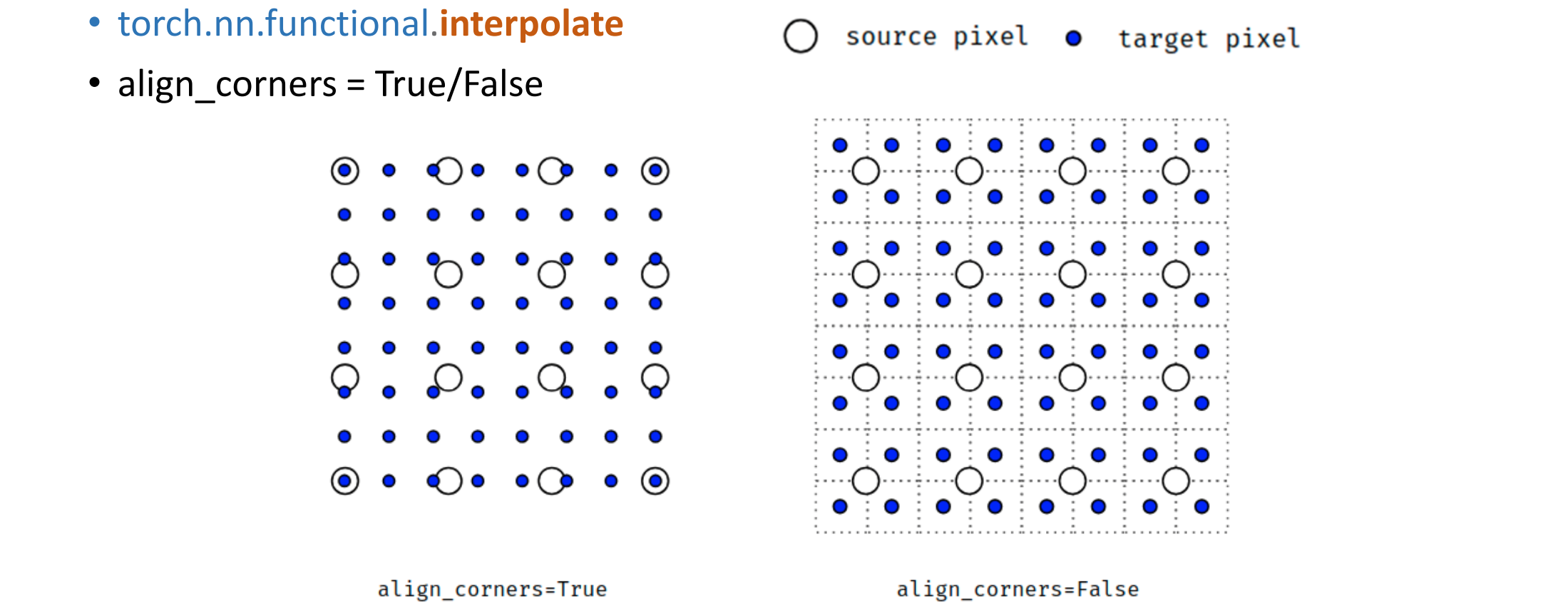
Interpolation(插值)
插值:插值是一种基于一组离散的已知数据点构建新数据点的方法
公式:其中,g:插值函数 ,h:采样增量 ,Xk:插值节点 ,Ck:采样数据上的参数 ,u:插值核 u(0) = 1,否则 u(k) = 0,(基函数、只影响某一部分)
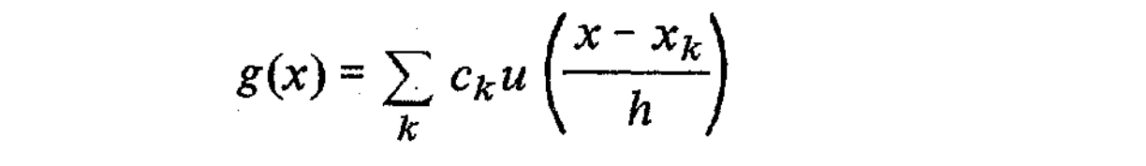
- 几种重要的插值:
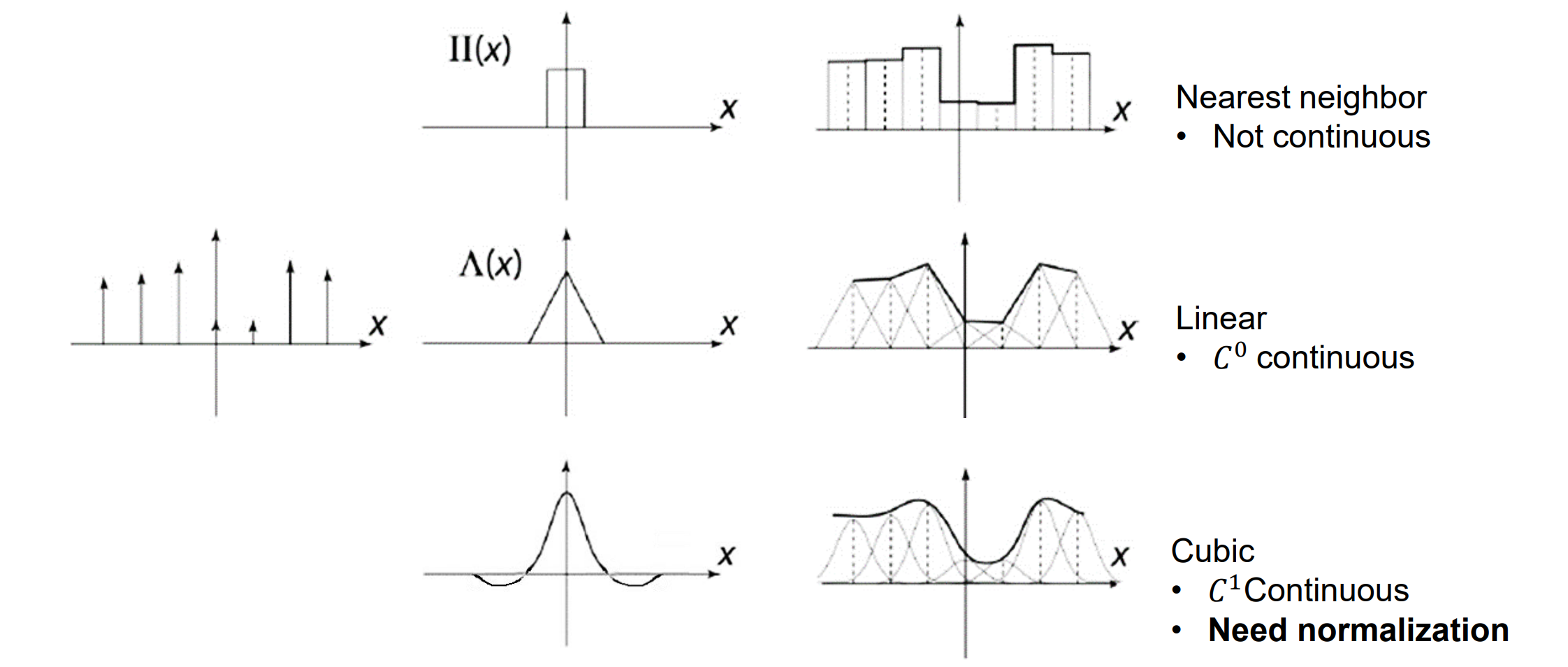
- 若基函数u是平台,则采用最近邻插值;线性插值除采样点外连续;若需要更高阶的连续性则需采用Cubic
Cubic Interpolation
- 从[-2,2],满足C1光滑,插值是对称的

Image Interpolation
双线性插值:图像插值通常可以先在一个方向上使用 1D 插值,然后再在另一个方向上使用 1D 插值来执行。双线性插值不是线性的 f(x,y) = a + bx + cy + dxy
双线性插值相当于对面积的加权平均
插值需注意:对角还是对边

Approximation vs Interpolation
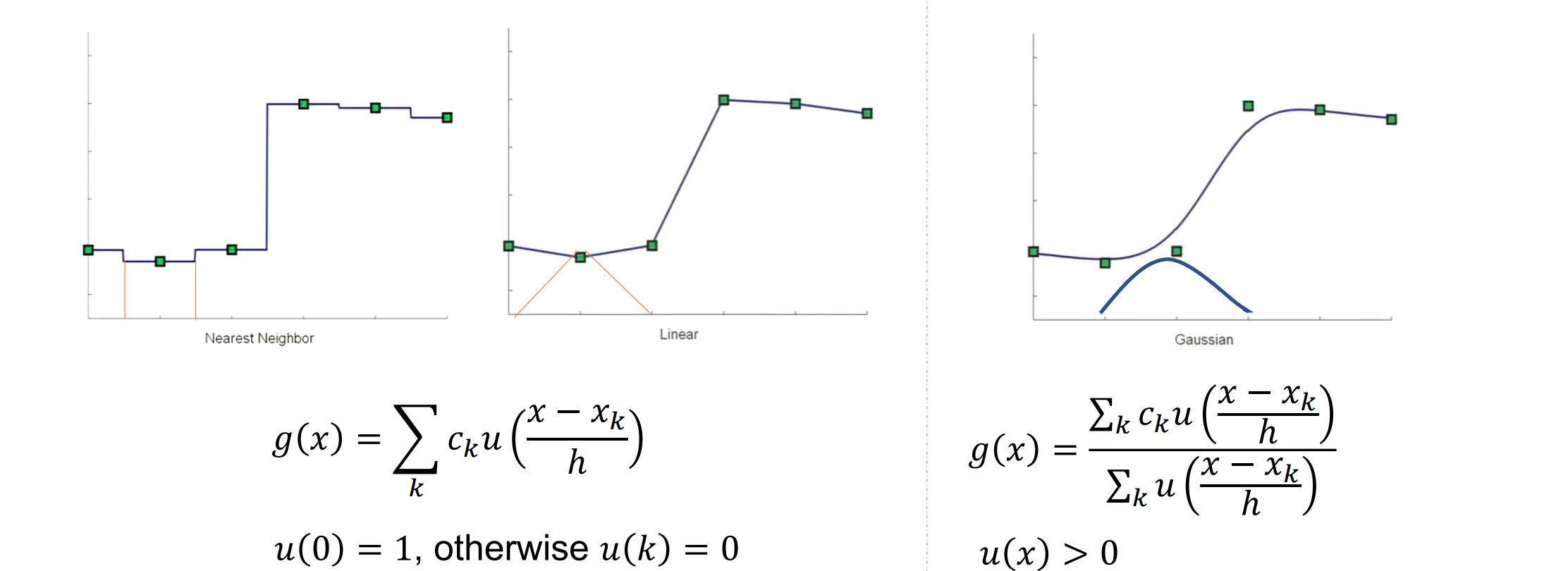
- 基函数近似的噪音更多
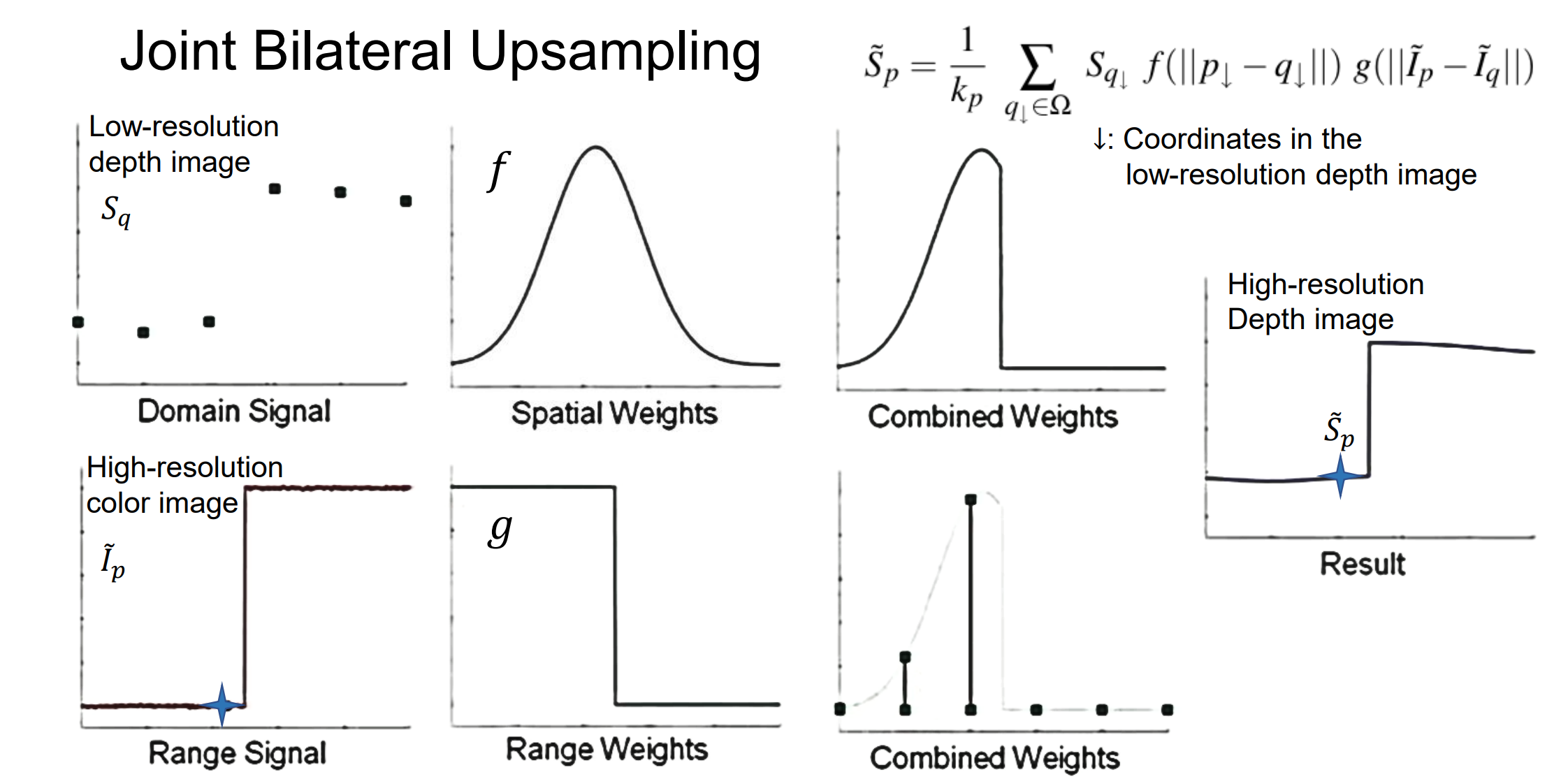
Joint Bilateral Upsampling(联合双边上采样)
提高速度:
- 降低输入图像的采样率
- 估计深度图像
- 对深度图像进行上采样
对结果进行上采样:重复使用原始输入图像中的边缘信息
Laplacian Pyramid
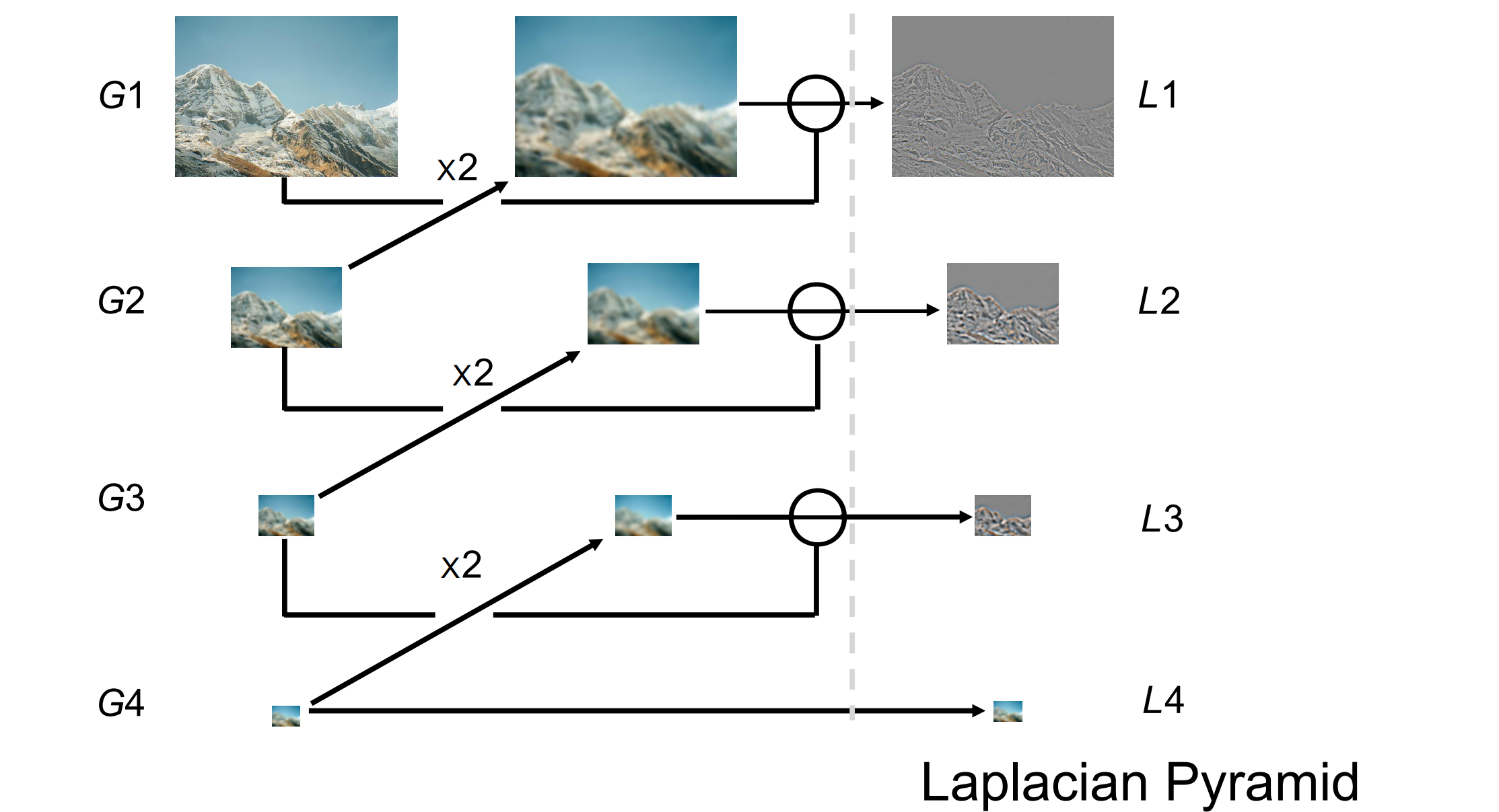
利用高斯滤波将高频过滤得到结果,将原始图像与输出图像相减得到“被过滤的部分”,在高斯金字塔中重复此操作得到拉普拉斯金字塔
Lx可以通过量化压缩(Compress by quantization)得到Gx
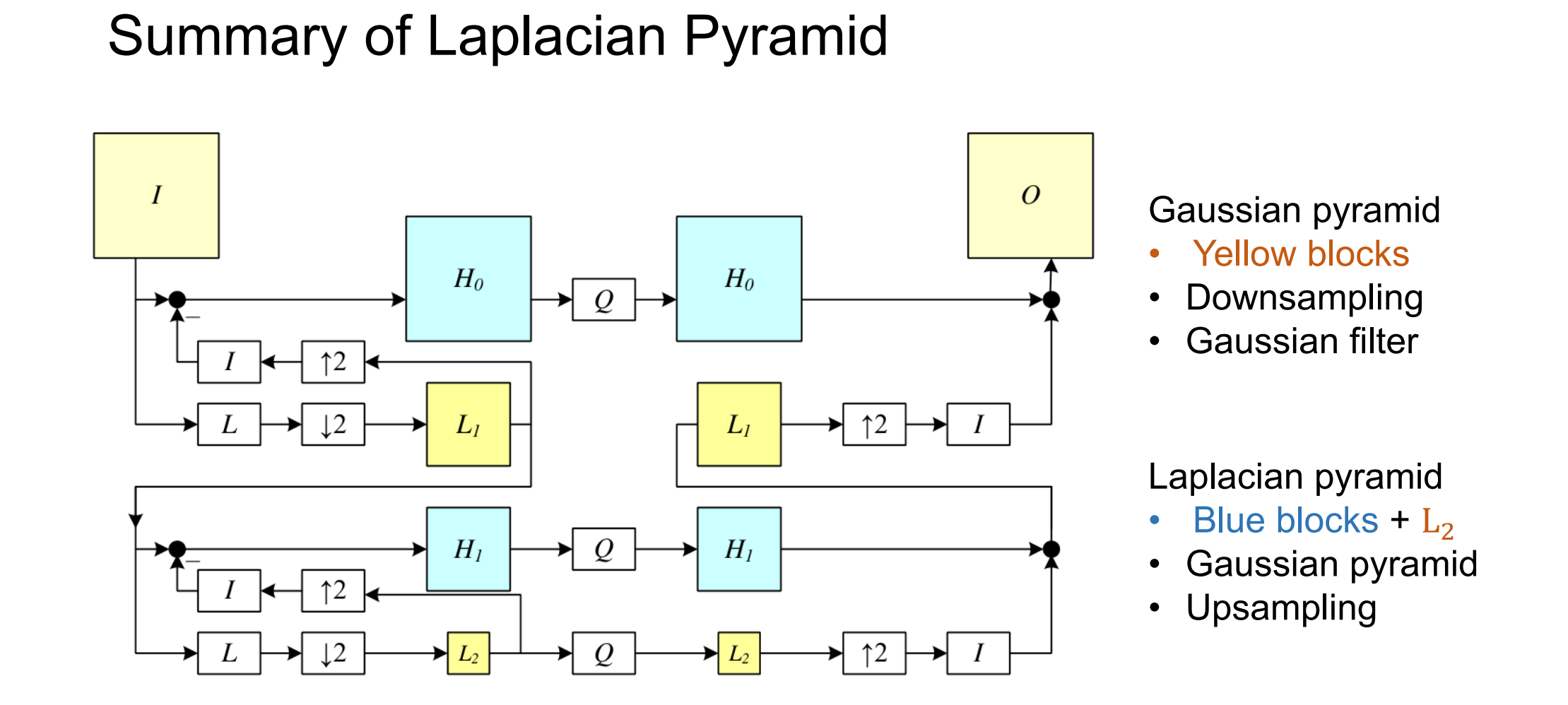
如果对高斯金字塔直接blur,则无法通过L,Q恢复原图。这些图像在理论上是相同的,但由于滤波/插值和边缘效果不完善,在实践中略有不同。而是需要下采样 + 上采样,以保证从 Laplacian Pyramid 完美重建 Gaussian
Laplacian Pyramid相比于Gaussian信号无冗余、按不同的频段放入不同的照片
Building a Laplacian pyramid:
- Create a Gaussian pyramid
- Take the difference between one Gaussian pyramid level and the next
Laplacian Pyramid: Image Blending
- 直接融合的问题:高频信息是正确的,而低频信息有误,例如交界处颜色不对,需要进行过滤。而Laplacian Pyramid可以得到不同频段的结果,因此对应不同频段的mask


- 关键思想:在较大的空间范围内混合低频带,在较小的空间范围内混合高频频带

Image Transformation
Geometric transformations(几何变换)
Image rotations or general warps
Forward Warping:For every pixel x in f(x)
- Compute the destination location x′ = h(x)
- Copy the pixel f(x) to g(x′)
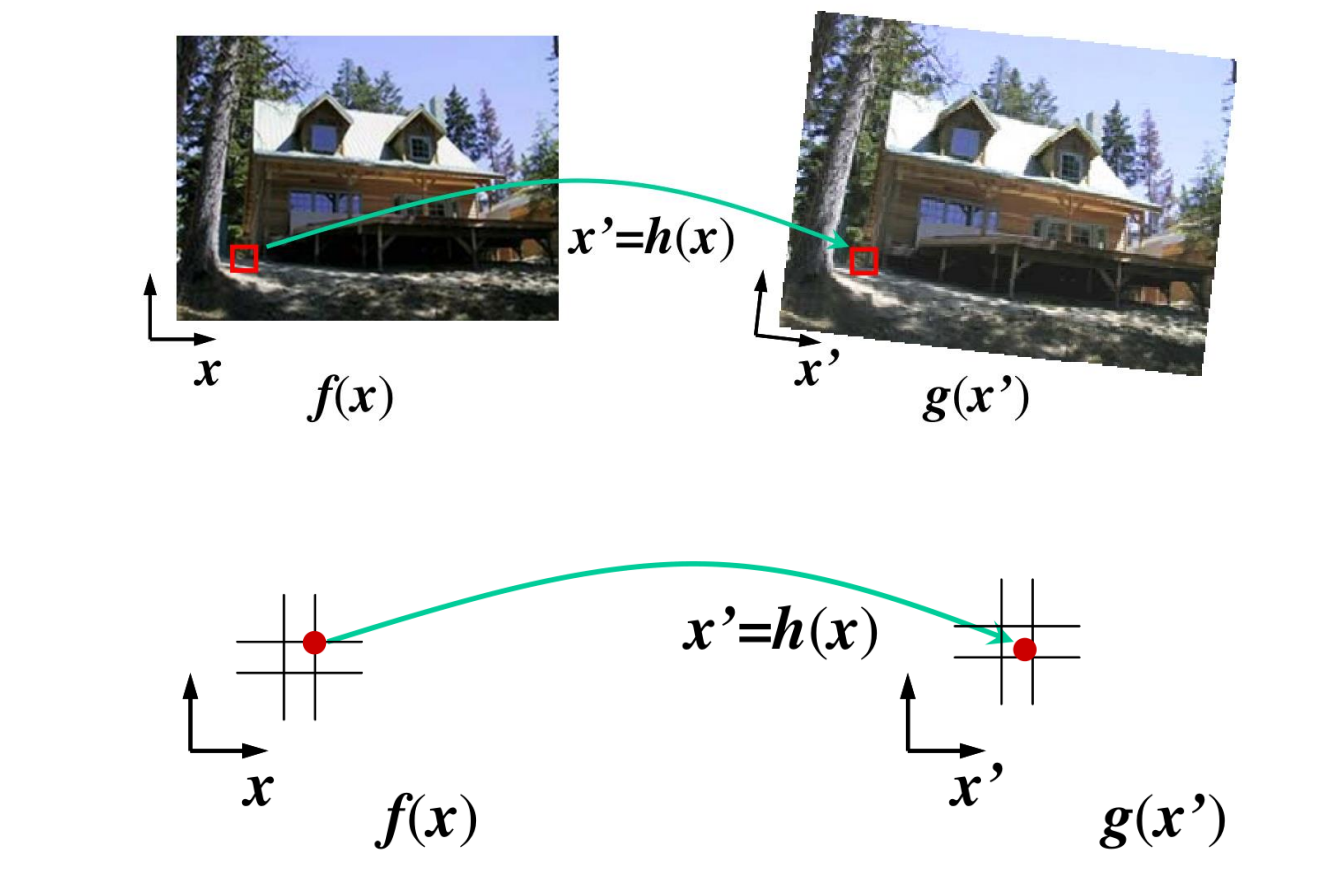
Forward Warping的局限性:
- 容易产生裂缝和洞
- x′ 可以是非整数
Inverse Warping(取反函数来计算):For every pixel x′ in g(x′)
- 用反函数ℎhat(x)计算源位置x
- 在位置 x 重新采样 f(x) 并复制到 g(x′)(用bilinear interpolation)
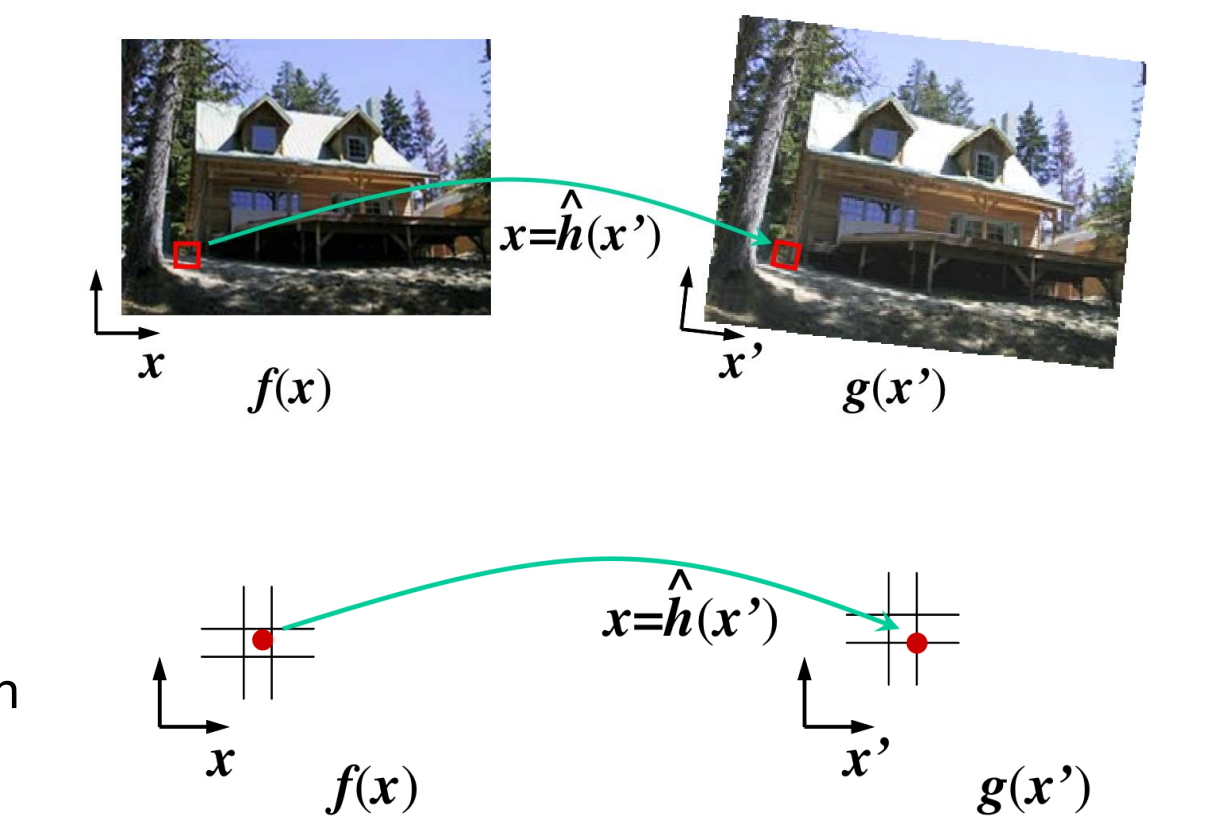
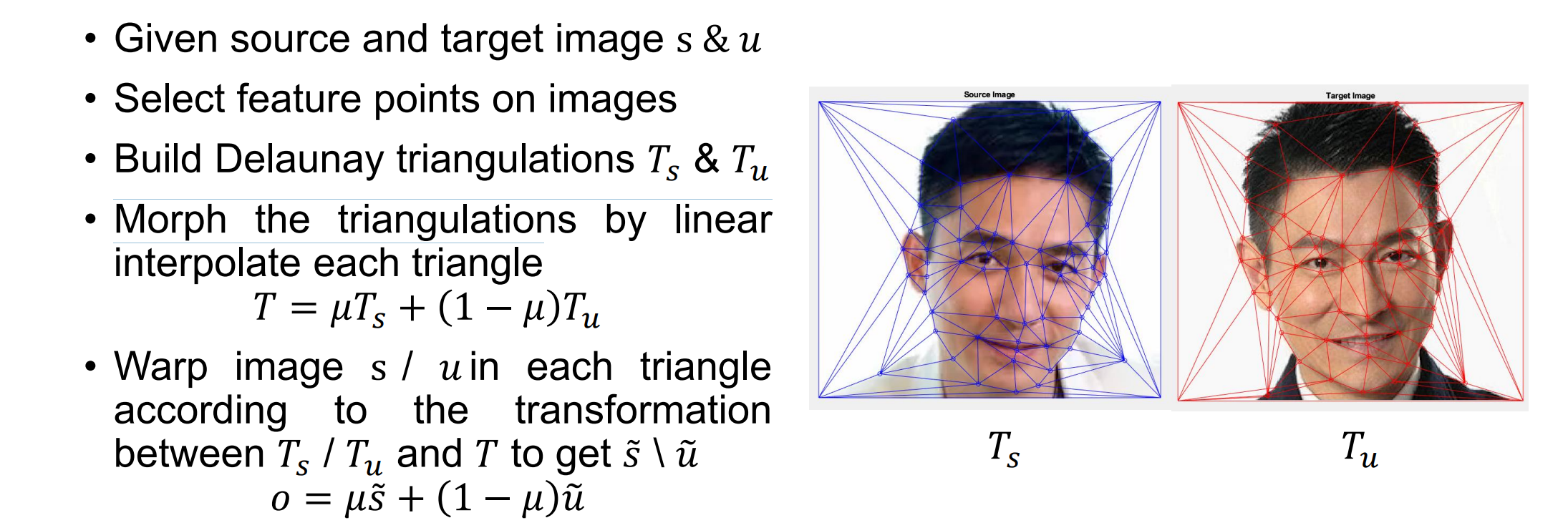
Image Morphing(图像变形)

- Image Morphing的具体步骤: