Photometric Stereo

  • 一个3D物体在不同的光照条件下重建法向量，再进一步求解三维

  • 通过在不同照明条件下观察对象的表面法线来估计该对象的表面法线

  • 为什么要估计法向：

    1. 法向量与颜色相关
    2. 法向量可以得到梯度从而得到平面

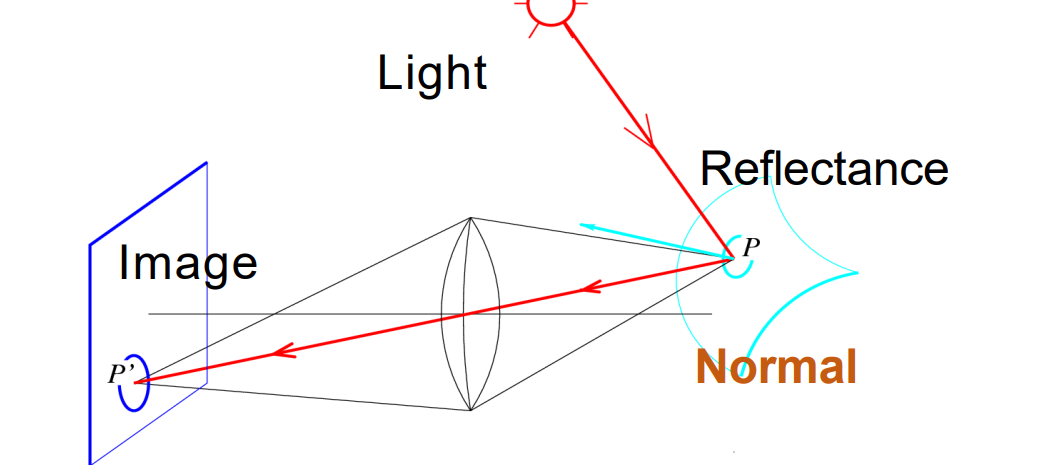
  • 输入：使用固定相机和不同的光照条件拍摄多张图像。相机不动，光线改变

image.png

Image Intensity

  • Image Intensity = 𝒇 (Light, Surface Reflectance,Surface Normal)。其中Intensity表示图像颜色，为已知。Light已知。Surface Reflectance反映了物体的材质为未知。Surface Normal为法向量为所求

  • 目标是从约束不足的图像强度中恢复法线

image.png

  • 解决歧义性：
    1. 多张图片消除歧义性
    2. 人为的增加假设或限制

Surface Reflectance

  • 镜面反射(Specular reflection)：光线围绕 Surface Normal 反射

  • 漫反射(Diffuse reflection)：光线向各个方向均匀散射

image.png

  • 此外还有折射、表面内传到和磷光等复杂现象

image.png

Surface Reflectance: BRDF

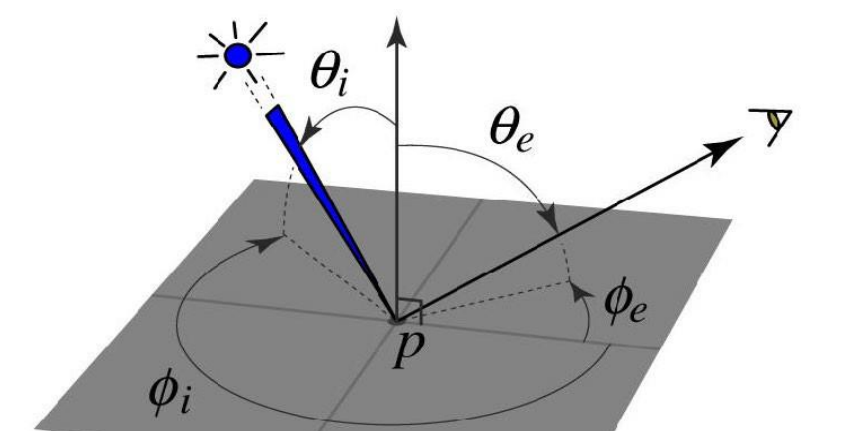
image.png

  • BRDF 是双向反射分布函数 （Bidirectional Reflectance Distribution Function） 的缩写

  • BRDF 描述了当光线从一个方向照射到表面上时，从一个方向观察表面时表面的亮度。是一个定义在半球上的分布函数

  • 光从某个角度打在半球上，称为冲击函数，散射到各个方向的分布密度为BRDF，其中i是入射相关变量，e是出射相关变量：

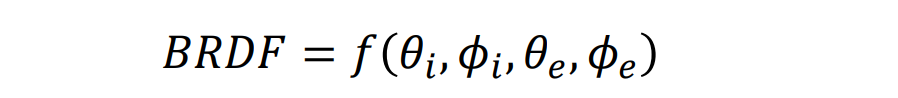
image.png

  • 为简单起见，我们主要关注漫反射

Diffuse Reflection

  • 此时BRDF均匀分布，对于每一个位置都是一个常数

  • Lambert’s Law for diffuse reflection：

image.png

  • I：反射强度，或每单位面积表面的总功率

  • ρ：反照率，表面反射的入射辐照度的分数，由材质决定

  • S：光的方向及其大小与其强度成正比。或者将光强储存在ρ中

  • n：单位表面法线

Surface Gradient and Normal

1.jpg

  • 从而推导出N = (p,q,1).其中p是-z对x求偏导，q是-z对y求偏导

Gradient Space

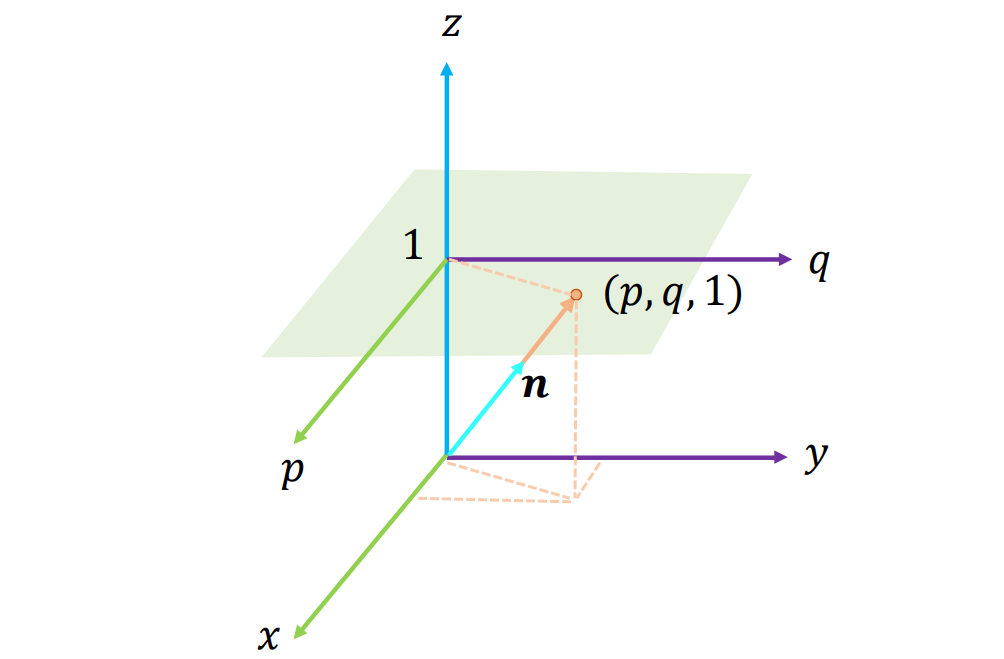
image.png

  • 平面 z = 1 称为梯度空间(Gradient Space)或 pq 平面(pqPlane)

  • Gradient Space 中的每个点 (p,q) 对应于一个唯一的方向:

image.png

  • 平面的法向和光源的方向都可以用p,q表达

Reflectance Map

  • 对于给定的光源 s 和表面反射率(材质)，点 x、y 处的图像强度 I 取决于点法线 （p， q， 1）

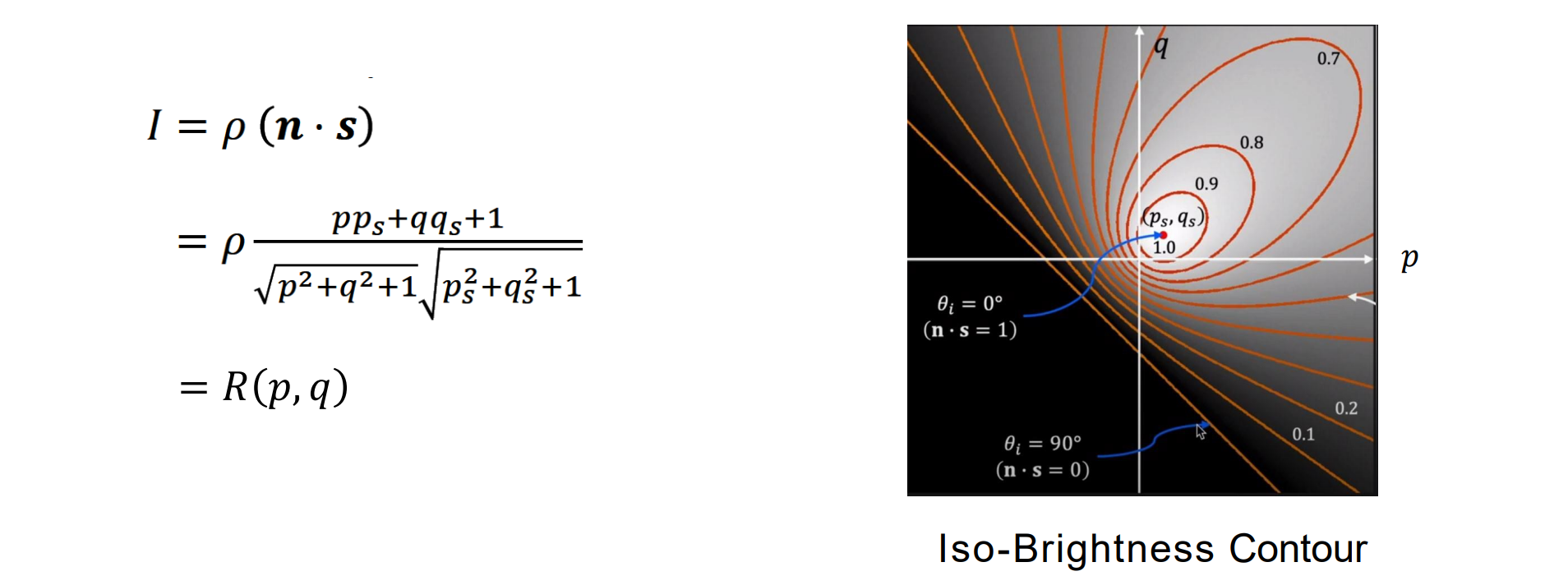
  • 描述此关系的函数是reflectance map:𝐼 = 𝑅(p,q)

  • 给定光源情况下，不同法向方向对应不同的颜色：法向方向和光源方向一样的时候亮度最高

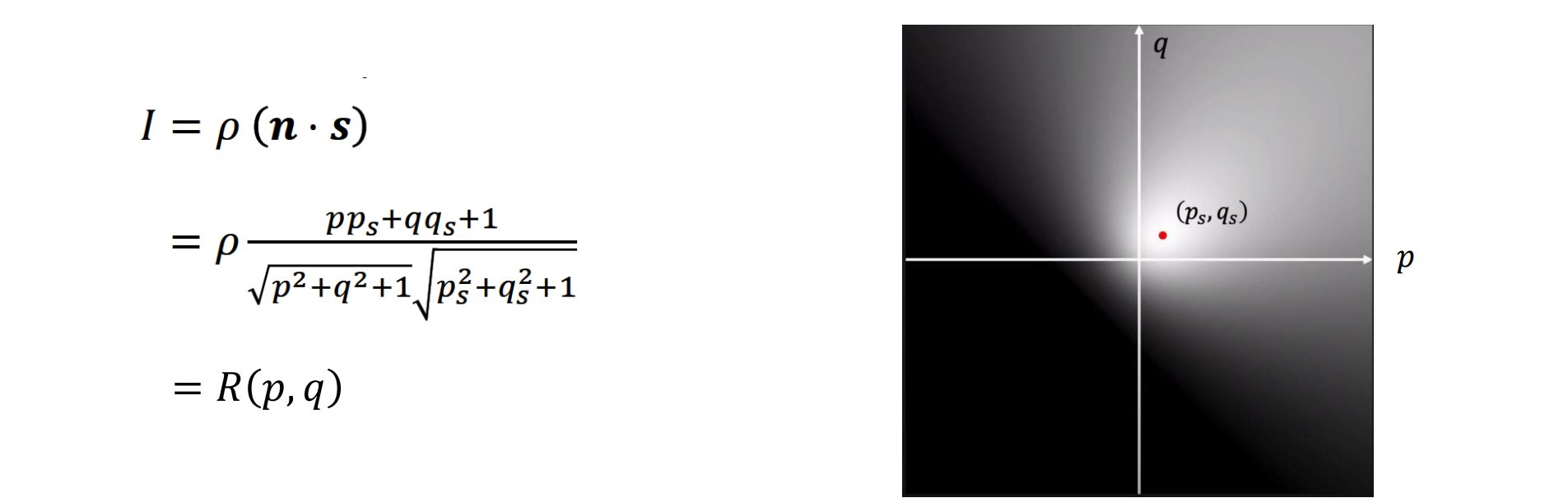
image.png

  • 等亮度线：以光源为中心，椭圆范围内的亮度一样，对应法向与夹角相等的方向

image.png

Photometric Stereo

  • 在不同光照下使用多个图像，解决表面方向的歧义性

  • 光源方向 i： si = (psi , qsi)。i已知即可求出reflectance map

  • 光源 i 的反射率图：Ri(p,q)

  • 光源 i 产生的光照强度：Ii（x， y）

  • 每张图片可求出该光照条件下对应reflectance map中的哪一个线，多张图片即可形成多条线在R(p,q)坐标系中相交，交点即为所求

image.png

  • 流程：

    1. 使用 K 个已知光源采集 K 张图像
    2. 使用已知的源方向和 BRDF，为每个源方向构建reflectance map
    3. 对于每个像素位置 x， y ，找到 p， q 作为 K 曲线的交点，这给出了像素 x， y 处的表面法线

  • K的最小值取决于材质，特殊情况下，对于漫反射，最小的 K 为 3

Photometric Stereo: Lambertian Case

  • 在三个光源下在 x、y 点处测得的图像强度：𝐼i = 𝜌𝒔i ⋅ 𝑁,i = 1,2,3

  • 可以写成矩阵形式：

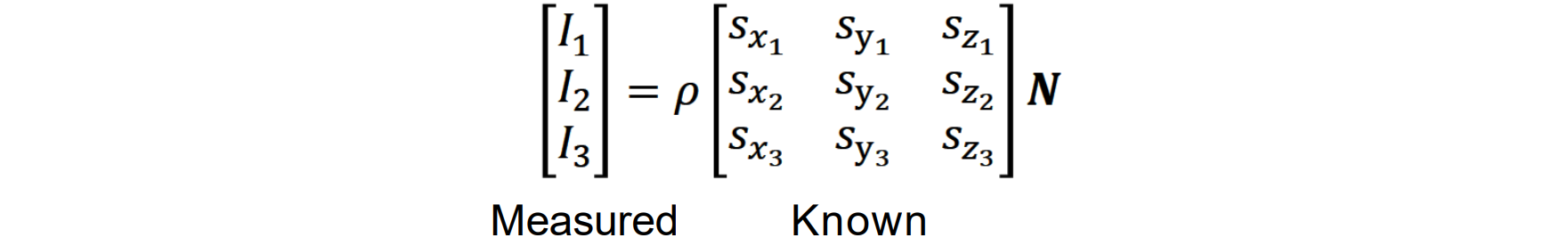
image.png

  • 可以使用单位长约束的最小二乘法求解，或求特征向量求解：其中，s1,s2,s3线性无关才能求解

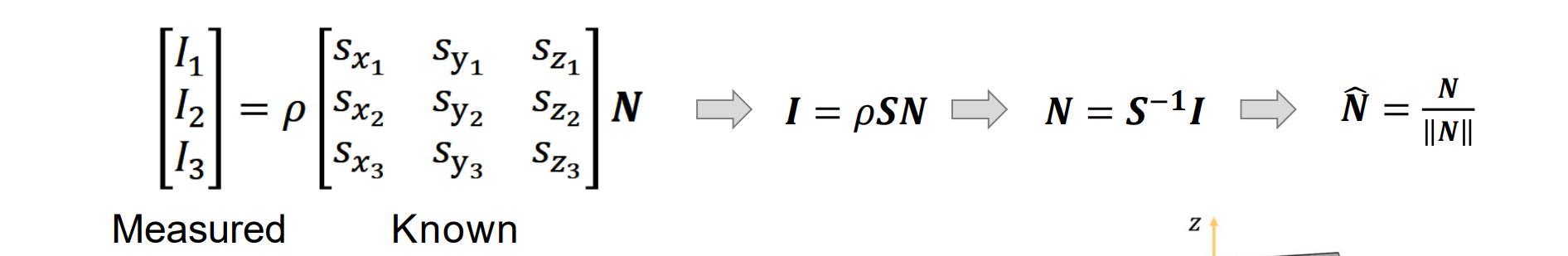
image.png

  • 使用更多 （K>3） 光源可以获得更好的结果：最小二乘法求解N

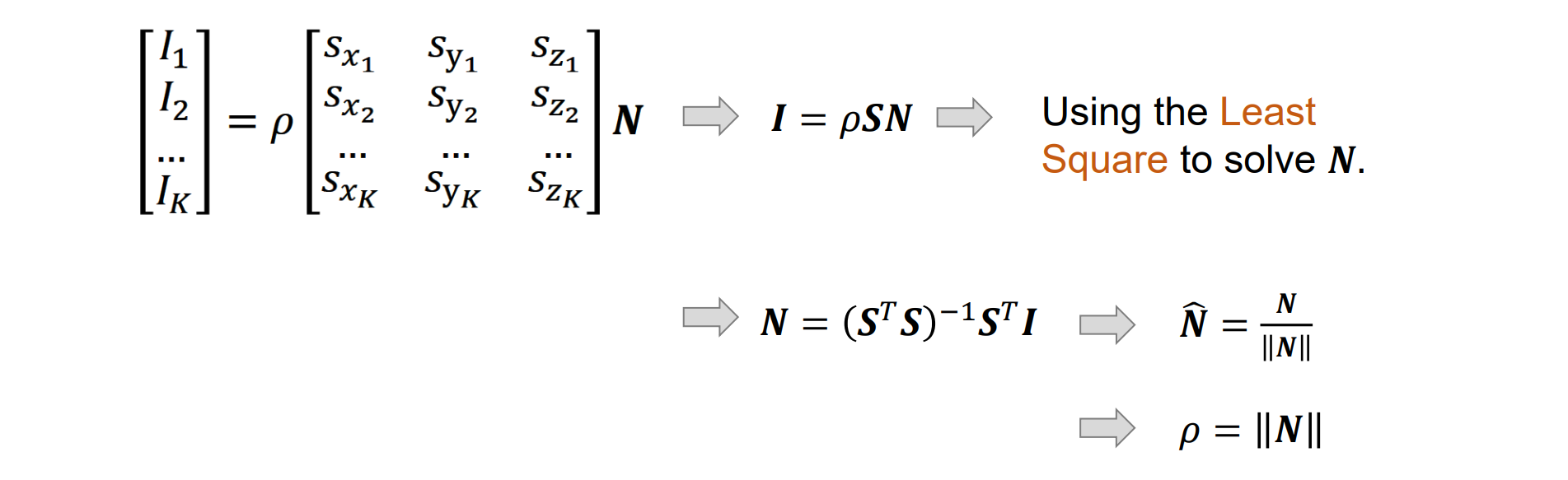
image.png

Calibration based Photometric Stereo

  • 前面的方法基于 Lambertian 假设，而更一般的情况不一定是漫反射的

  • 这里我们介绍一种通用反射率模型的方法：使用已知大小、形状（例如球体）和与场景对象相同的反射率的校准对象。例如想要重建某个物体可以先用同样材质造一个球

image.png

  • 方向一致性：具有相同表面法线的点在不同照明下产生相同的强度集（忽略全局照明）

  • 流程：

    1. 在 K 个不同的光源下捕获 K > 3 张图像。球体上的每个点都会产生对应于 K 光源的 K 图像强度 I1，I2， … ，IK
    2. 使用球体的已知大小，计算球体上每个点的表面法线(p,q,1)
    3. 为 K 元组创建查找表：(I1，I2， … ，IK) → (p,q),对应K个颜色值，每个点构造查找表
    4. 在相同的 K 个光源下捕获场景对象的 K 个图像
    5. 对于场景中的每个像素，使用查找表映射 (I1，I2、… 、IK) → (p,q)

Shape from Normals(本质：做积分)

  • 输入：梯度/法向量图

  • 输出：深度/形状图

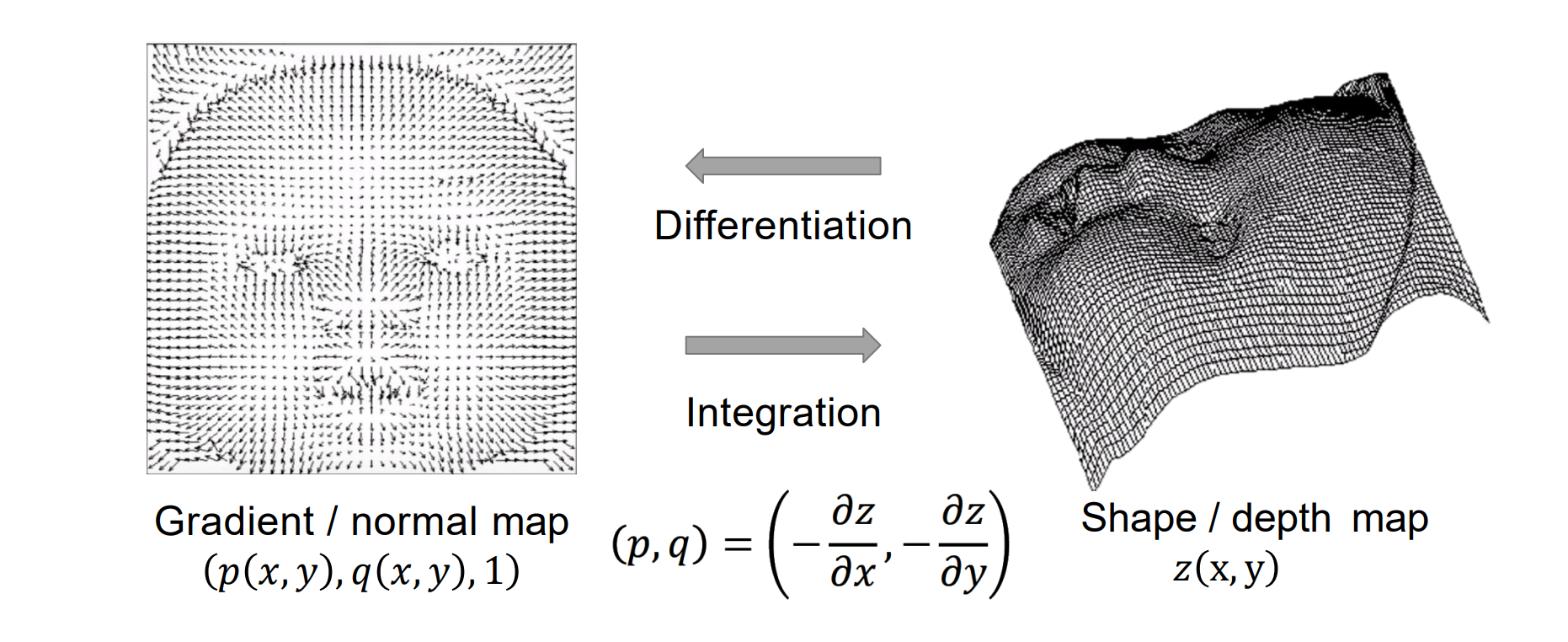
image.png

Shape from Normals: Integration-based Method

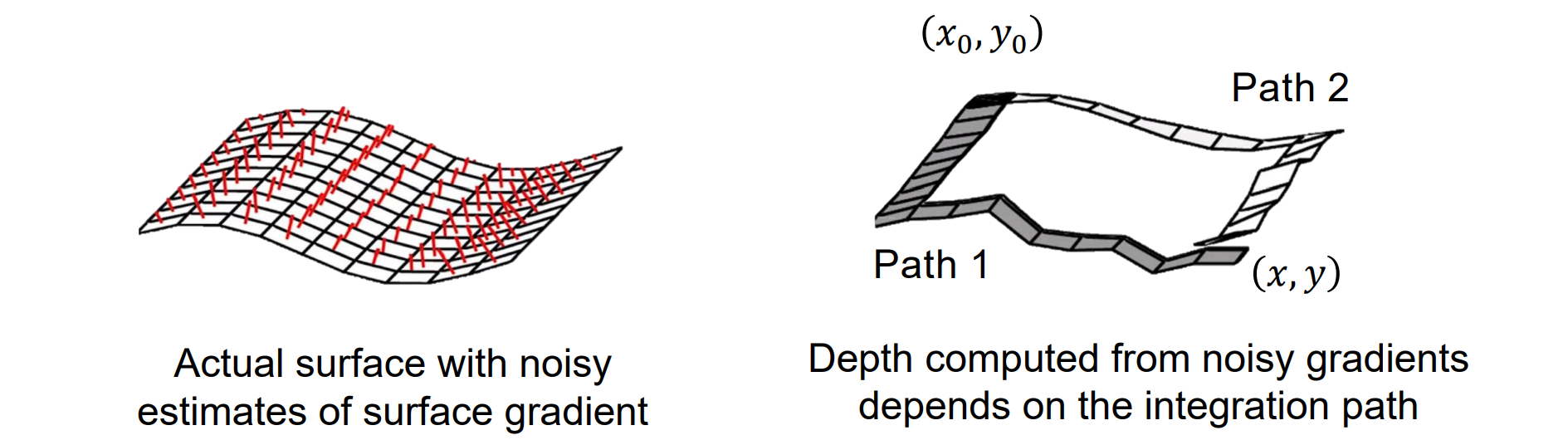
  • 格林公式(第二型曲面积分)：积分与路径无关

image.png

  • z（x， y） 可以通过从参考点 x0， y0 沿任何路径积分获得

  • 将 z（x0， y0）定义为 0

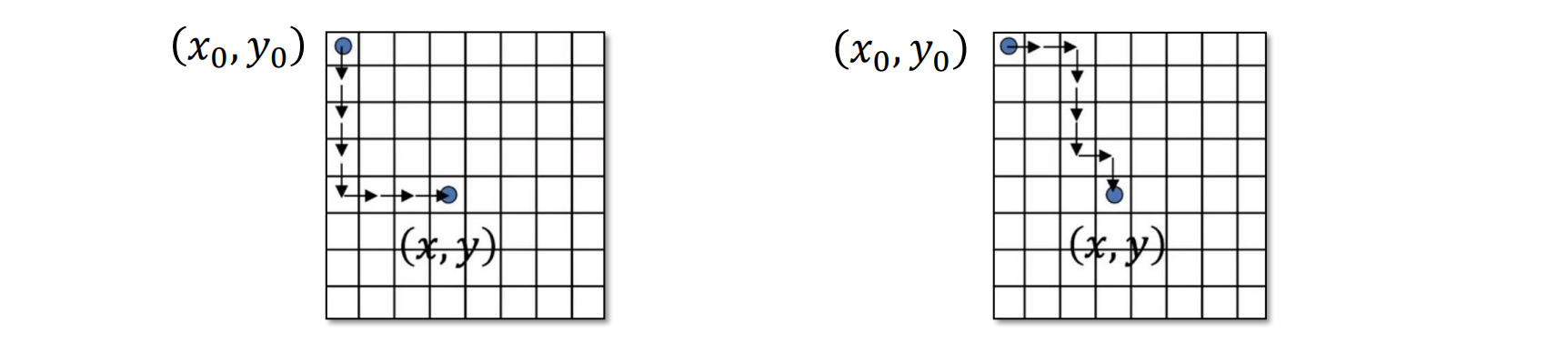
image.png

  • 现实中会有误差，由于积分与路径无关，因而可以多选几个路径求平均

  • 流程：

    1. Initialize the reference depth 𝑧 (0,0) = 0
    2. 计算第一列的深度值:
      for 𝑦 = 1 𝑡𝑜 𝐻 − 1
      𝑧 (0, 𝑦) = 𝑧 (0, 𝑦 − 1) − 𝑞 (0,𝑦)
    3. 计算每行的深度值:
      for 𝑦 = 1 𝑡𝑜 𝐻 − 1
      for 𝑥 = 1 𝑡𝑜 𝑊 − 1
      𝑧 (𝑥, 𝑦) = 𝑧 (𝑥 − 1, 𝑦 − 1) − 𝑞 (𝑥, 𝑦)

  • 一种解决方案：使用不同的路径计算深度图，并找到计算的深度图的平均值以减少错误

image.png

Estimating Shape using Least Squares(类似泊松方程)

  • 最小化测量的表面梯度与估计表面的表面梯度之间的能量函数：

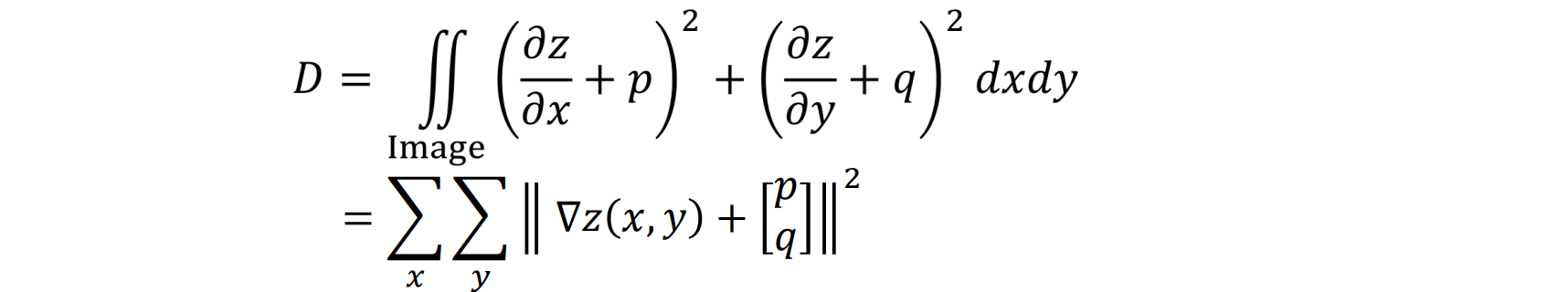
image.png

  • 得到的线性方程组也称为泊松方程

  • 可以用最小二乘球z

Shape from Shading

  • Shape from Shading, a special case of photometric stereo

  • 输入：图像 I、源方向 s 和surface reflectance model

  • 输出：每种intensity的表面梯度 （p， q）

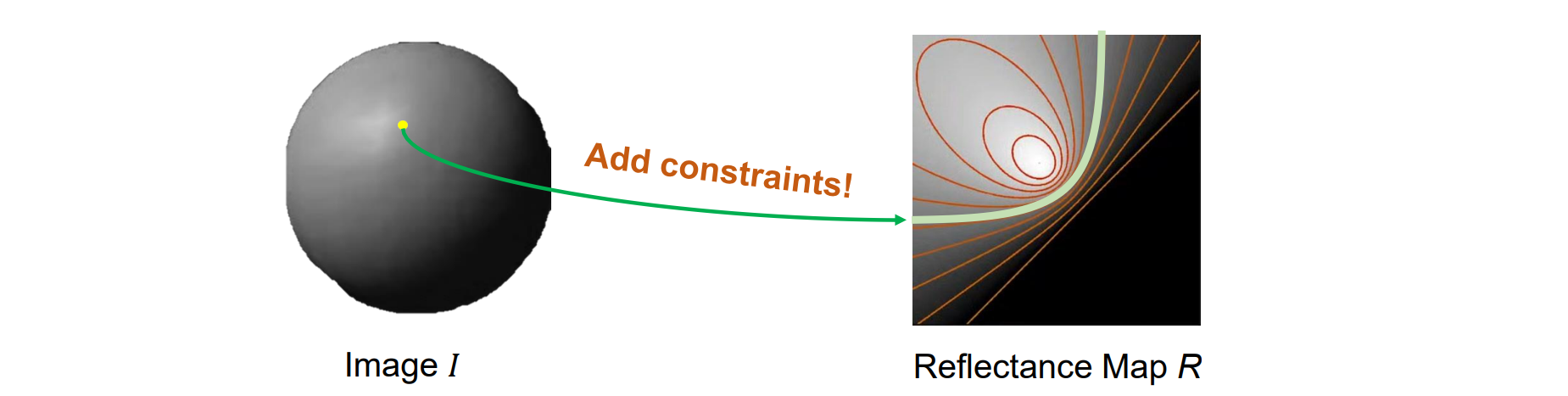
image.png

  • 一个点对应reflectance map中的一条线，需要人为的增加约束才可求解

Constraints from Human Perception:

  • Light from Above

image.png

  • Boundaries Influence Perceived Shape

image.png

  • 均匀明暗变化

  • 根据周围的物体感知形状

Stereographic Projection

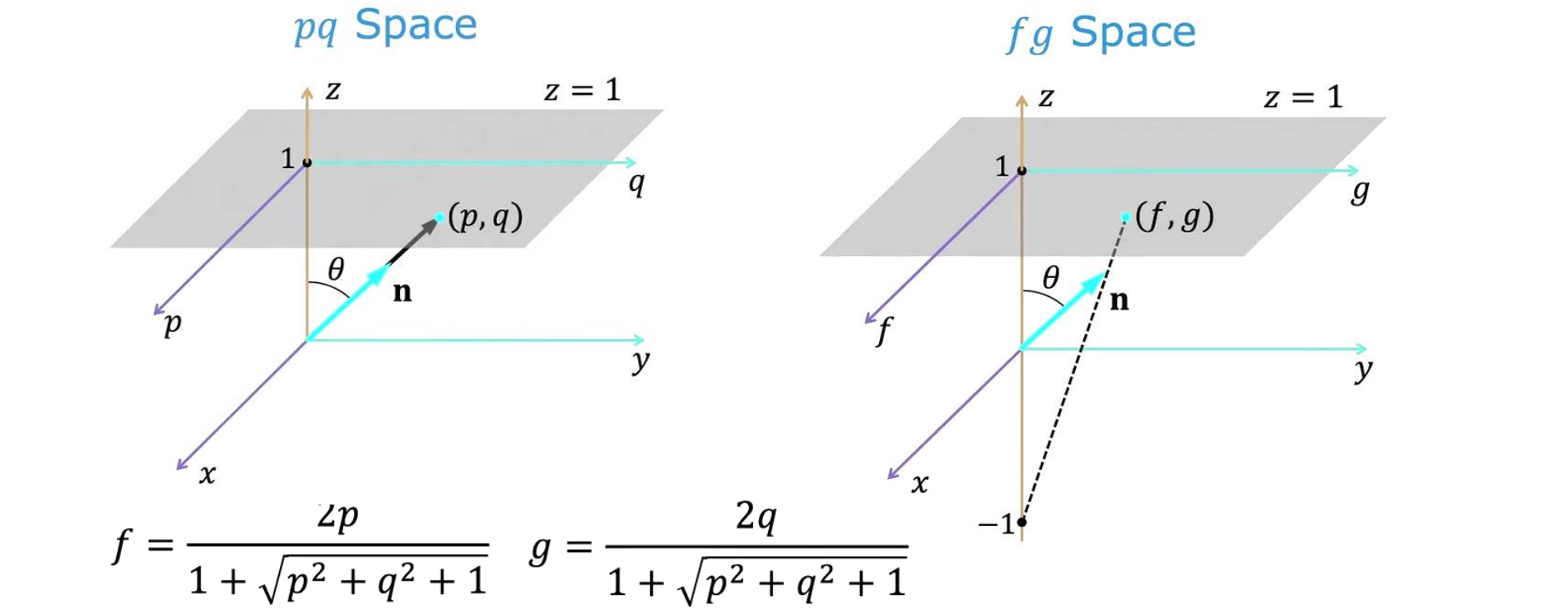
  • Gradient Space的问题：𝑝 or 𝑞 is infinite when 𝜃 = 90°

  • 将原点上移形成fg space，错开求交，数值更稳定，可以通过p,q求得f,g

image.png

  • 半球上可见的表面渐变的所有可能值都位于 fg 平面上半径为 2 的圆内：I = R (f，g)

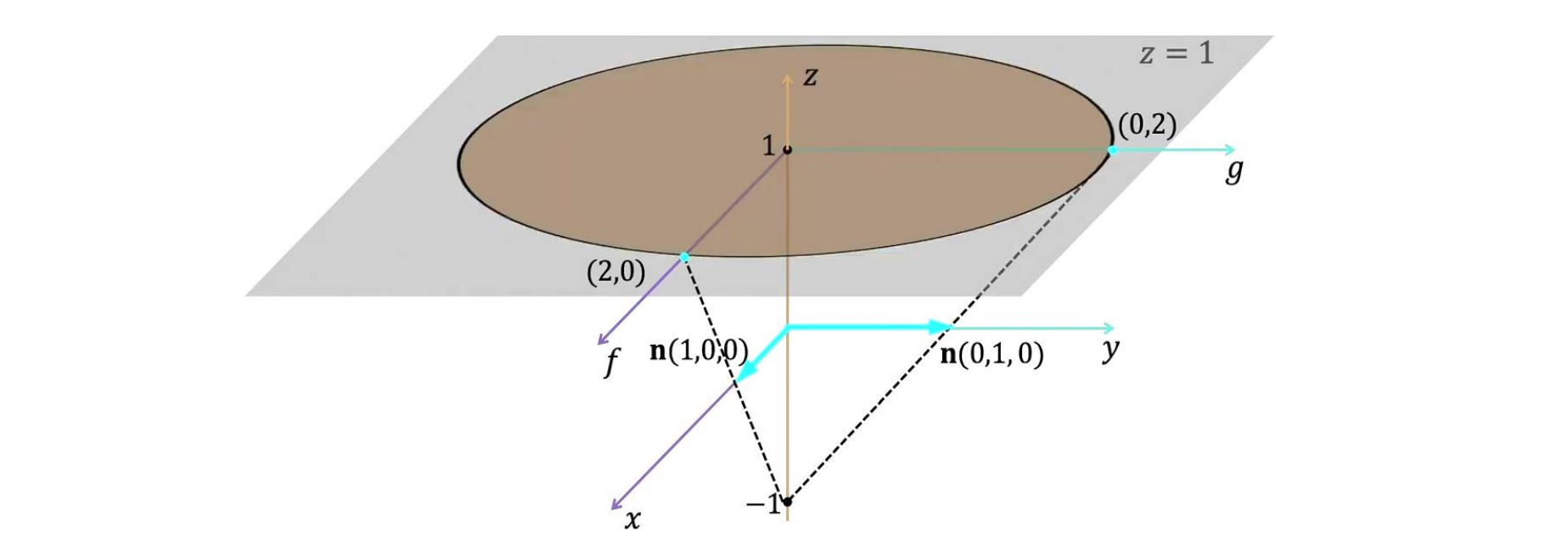
image.png

Occluding Boundaries Constraint(边界约束)

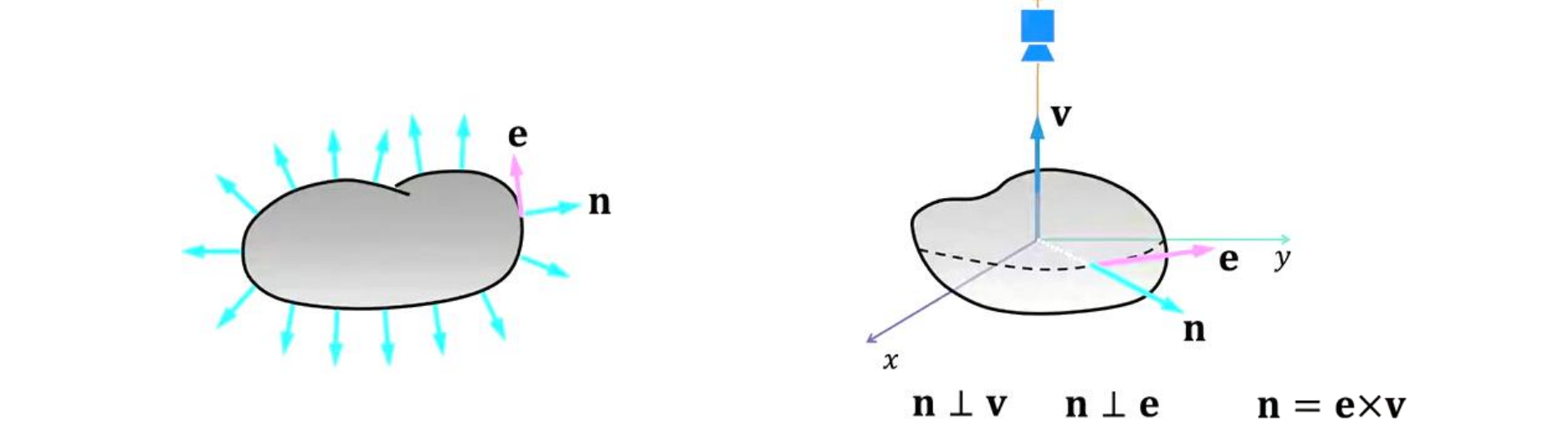
image.png

  • n 是边界上的表面法线，e 是边界上的边方向，v 是视图方向。可以通过叉乘得到n的方向

  • 遮挡边界上的表面梯度 f、g 是已知的，可以用作边界条件

Image Intensity Constraint

  • 假设：图像强度（辐照度）应等于反射图：I (x，y) = Rs (f，g) ，也可以视为数据项

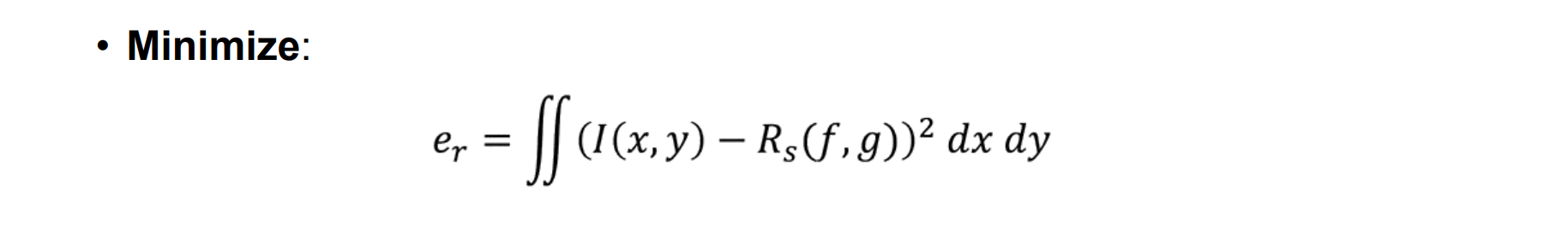
image.png

  • 目标：惩罚图像辐照度和反射率图之间的误差

Smoothness Constraint

  • 假设：对象表面是平滑的。也就是说，梯度值 （f， g） 变化缓慢

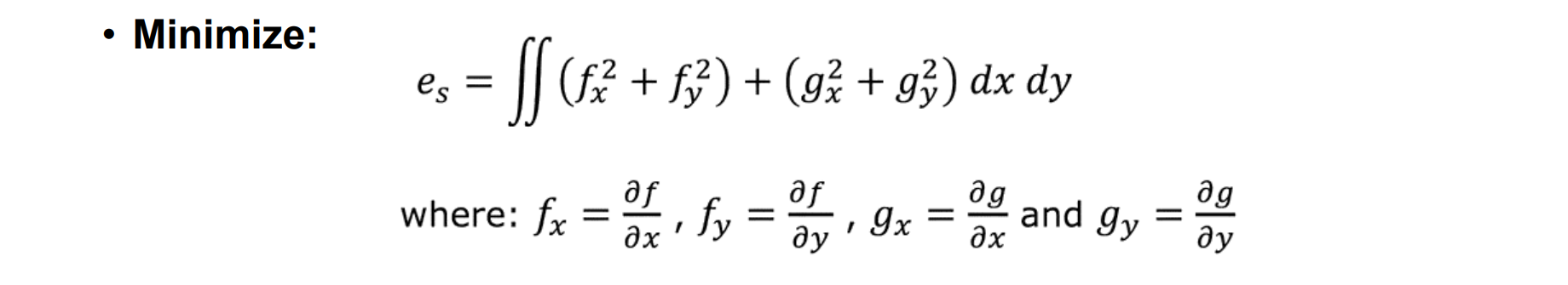
image.png

  • 目标：在表面估计过程中惩罚 f 和 g 的快速变化

Shape from Shading

  • 查找最小化函数的所有图像点的表面梯度 （f， g）：

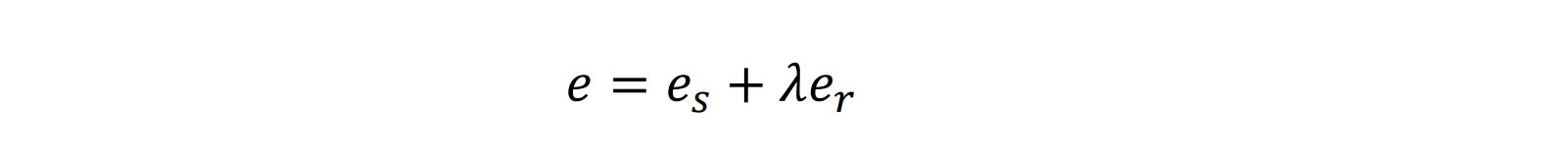
image.png

  • 其中 es 是平滑度约束，er 是图像辐照度误差，λ 是权重

  • 遮挡边界上的已知表面梯度 （f， g） 保持为常数

  • 可以使用优化算法和数值迭代算法求解：

image.png