Structure from Motion

  • 输入：多张照片

  • 输出：相机的参数以及位置和场景的3D模型

image.png

Structure from Motion vs Calibration & Triangulation

  • Calibration：

    1. 输入：从 3D 到 2D 的点对
    2. 输出：相机参数

  • Triangulation:

    1. 输入：相机的参数和2D点对
    2. 输出：3D点

  • Structure from Motion

    1. 输入：2D到2D的点对
    2. 输出：3D点以及相机参数

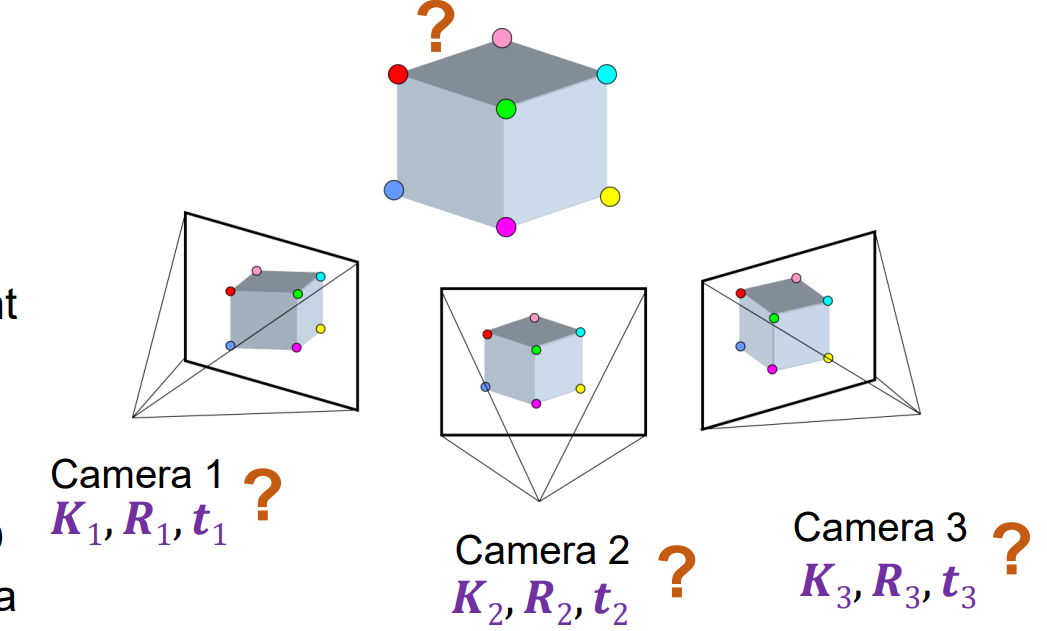
image.png

Structure from Motion: Problem formulation(问题设置)

  • 输入：n 个固定 3D 点的 m 个图像（忽略可见性），使得：Pi是第i个相机的参数，Xj是3D其次坐标，二者均为未知。Xij是第i张图片的投影点

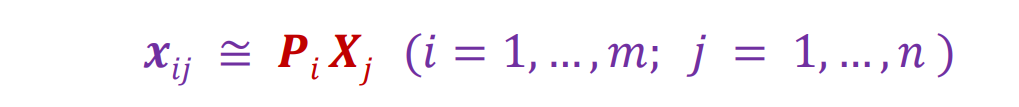
image.png

  • 输出：估计 m 个投影矩阵 Pi 和 n 个 3D 点 Xj 来自 mn 对应关系Xij

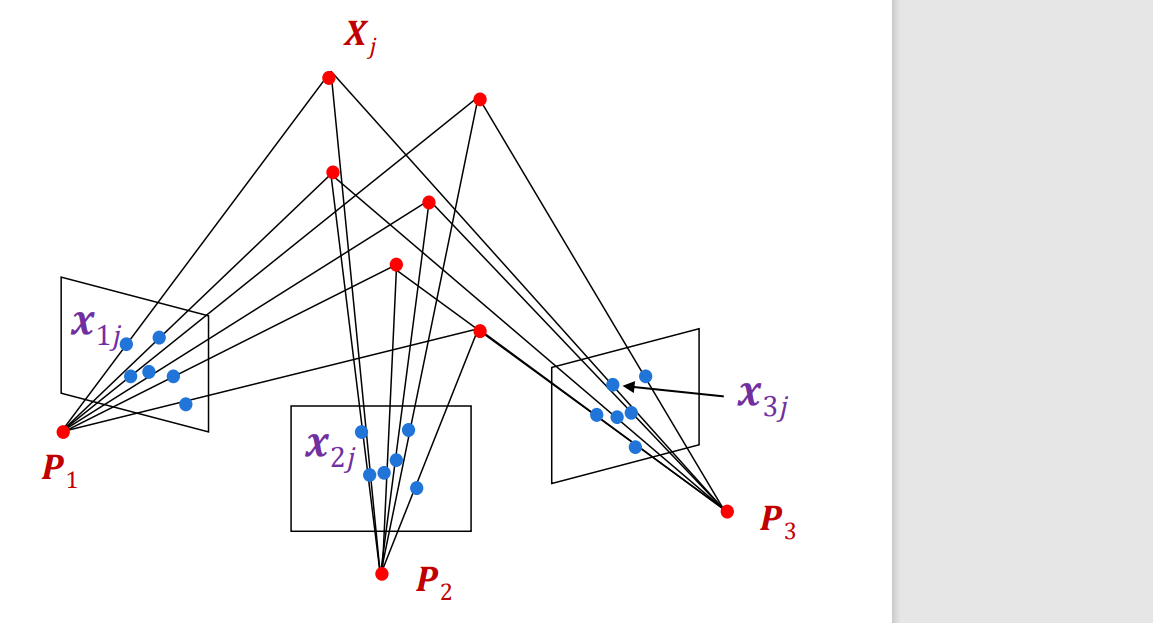
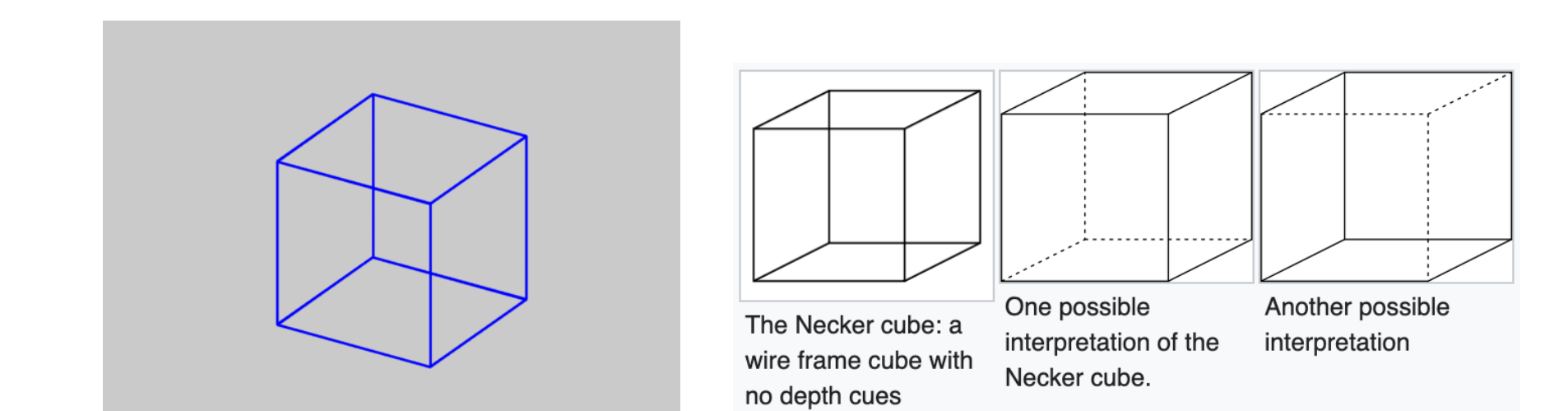
image.png

The Ambiguity of Structure from Motion

  • SFM有歧义性是不可解的，因此必须加以约束才可解出唯一值，否则会得到一族解。例如下图对同一个场景，相机既可能来自右上方，也可能来自左下方

image.png

  • 缩放歧义性：将场景缩放 k 倍，并将摄像机矩阵缩放 1/k，然后场景的投影将保持完全相同。没有参考测量，就无法恢复场景的绝对比例，只能重建相对尺寸不变

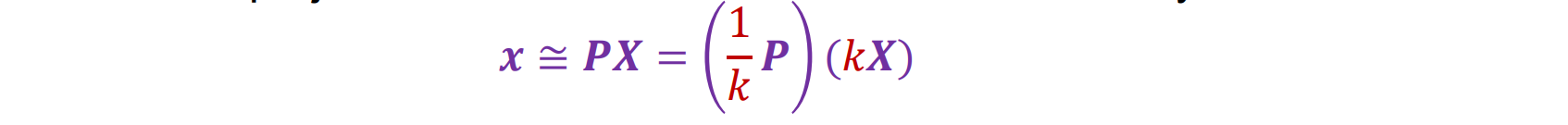
image.png

  • 如果我们使用变换 Q 变换场景并将逆变换应用于相机矩阵，则图像观测值不会改变：

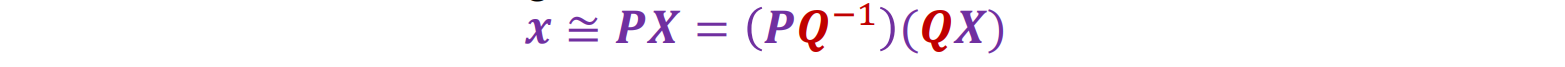
image.png

Projective Ambiguity

  • Q没有任何约束的时候，会产生投影歧义性

image.png

  • 此时Q是4x4满秩矩阵

Affine Ambiguity(仿射歧义性)

  • 如果我们施加并行约束，我们可以得到一个达到仿射歧义性的重建。约束Q的最后一行为[0…0,1]，仿射歧义性能保持平行关系

image.png

image.png

Similarity Ambiguity(相似歧义性)

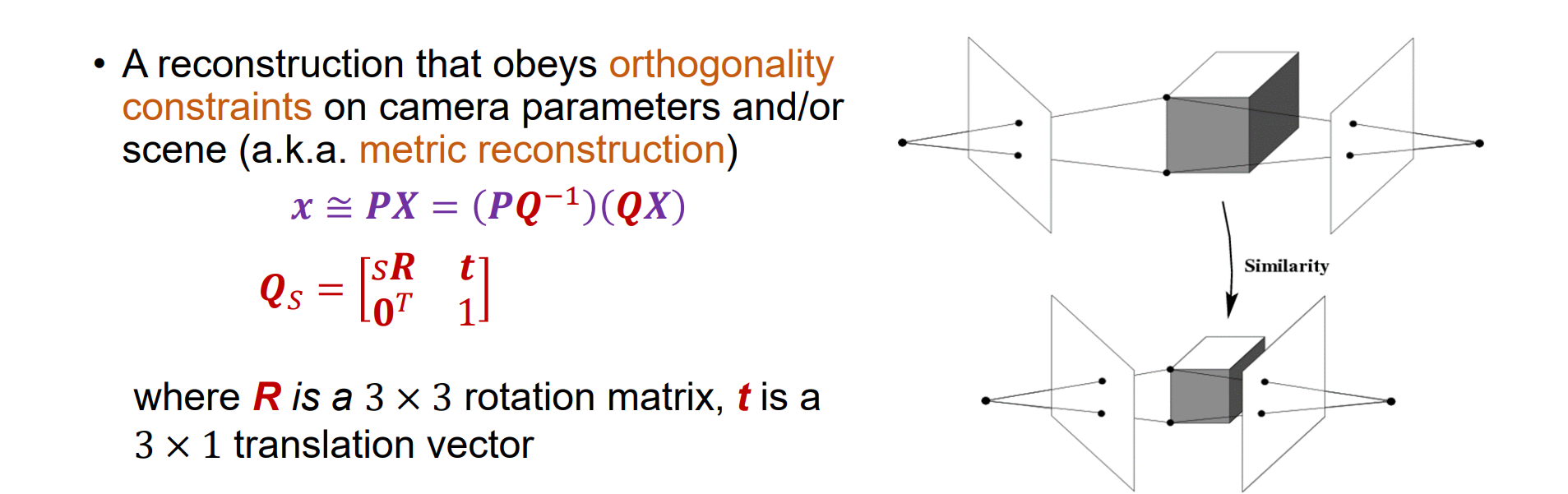
  • 遵循摄像机参数和/或场景的正交性约束的重建（也称为度量重建）。限制Q只包含缩放，旋转或平移可重建达到相似歧义性。能保证直角不变，和真实世界保持相似关系

image.png

image.png

Affine Structure from Motion

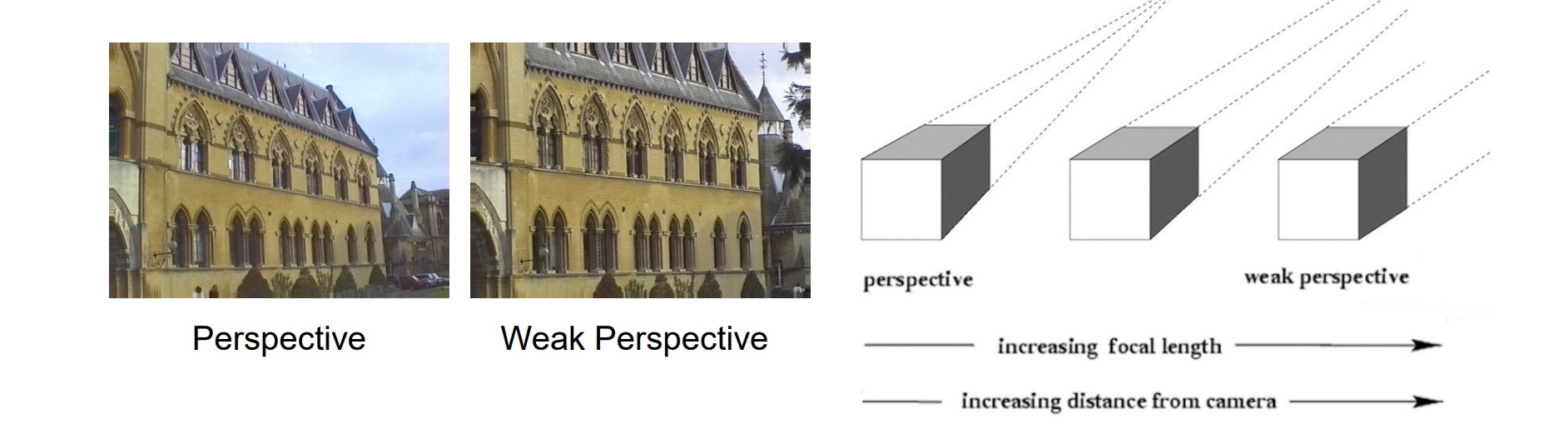
  • affine or weak perspective cameras(弱视角相机)：假设相机距离物体很远的时候，可以近似用正交矩阵估计投影矩阵以简化数学计算

image.png

  • 正交矩阵：丢弃掉3D点的Z坐标

image.png

Affine Camera

  • 在正交投影下，相机矩阵可以写成如下形式。其中第一个矩阵代表内参，即2D仿射变换，第二个矩阵为正交投影矩阵，第三个矩阵对应3D齐次坐标变换

image.png

  • 将此相机称为仿射相机，将用它来执行 SFM

  • 投影矩阵是 3D 到 2D 线性映射加上平移：，写成分块矩阵形式如下：其中，t是平移量

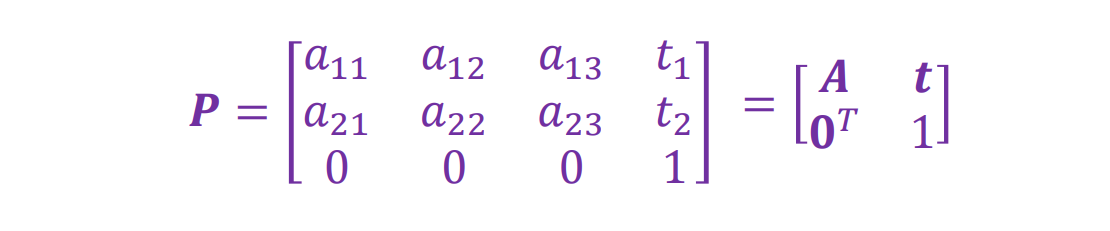
image.png

  • 在非齐次坐标中：其中将第一行记为a1,第二行记为a2,则a1,a2为投影矩阵的两个基(投影轴)，写成AX+t可得t是世界坐标系的原点坐标的投影(t1,t2)

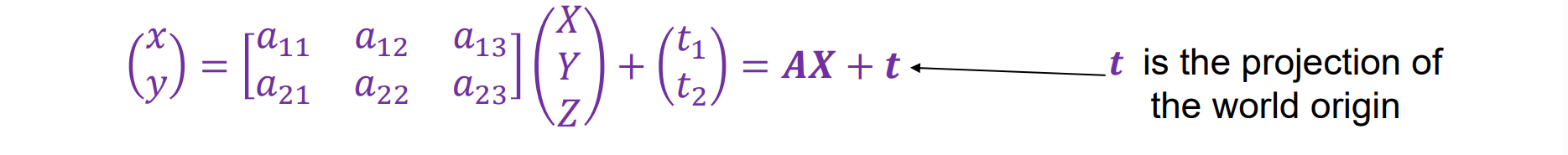
image.png

  • Affine Structure from Motion给出n 个固定 3D 点的 m 张图像，使得：其中红色部分的A,X,t都是未知

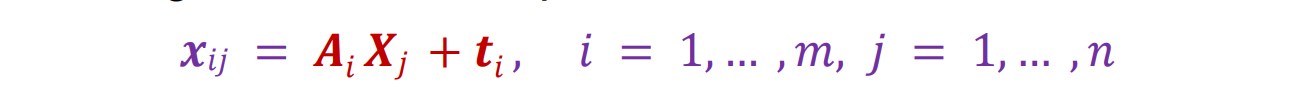
image.png

  • 使用 mn 对应关系 xij 估计 m 个投影矩阵 Ai 和平移向量 ti 和 n 个点 Xj

  • 重建定义为具有 12 个自由度的任意仿射变换 Q：

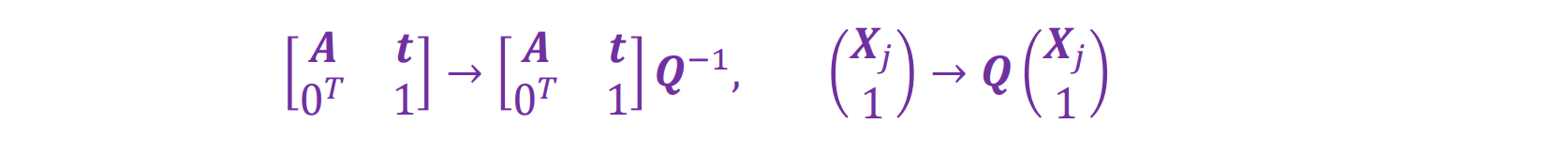
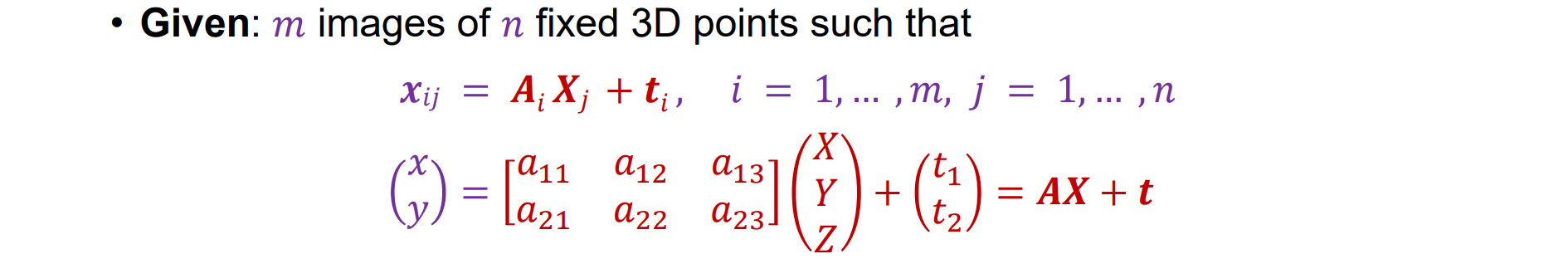
image.png

image.png

  • 一个点关于x,y各得一个方程，一个点得到两个方程

  • 2mn个已知变量(xij)，8m+3n个未知变量(Ai,ti和Xi)

  • 为了能够解决这个问题，我们必须有 2mn ≥ 8m + 3n − 12，因为仿射歧义性带走了 12 个自由度

  • 而对于两个图片，即m=2，可得n≥4，至少需要4个对应点

  • 化简技巧1: centering:通过减去每个视图中图像点的质心来使数据居中，即将投影点归一化。先计算平均点，再将原点平移到平均点的位置

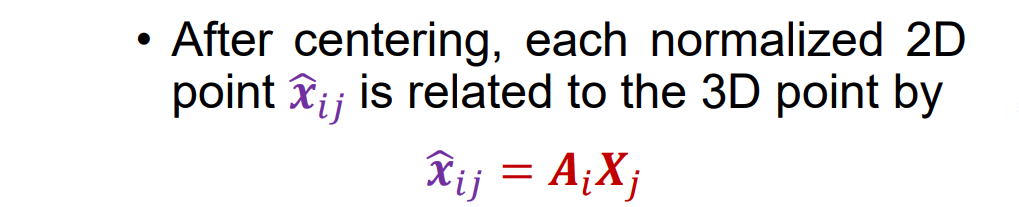
image.png

image.png

  • 通过将世界坐标系的原点定义为 3D 点的质心，无需将 3D 数据居中（和平移歧义）

image.png

  • 上述公式展开中：m是相机索引，n是点的索引，Ai是投影矩阵，Xi是投影坐标点

  • 根据矩阵秩将 M、S 从 D 分解：D = MS。D的秩一定为3，因为M的秩为3，且D的秩为3

Factorizing the Measurement Matrix

  • 根据矩阵秩从 D 分解 M、S:SVD 分解：Mm×n = Um×m ⋅ Σm×n⋅ Vn×n.T

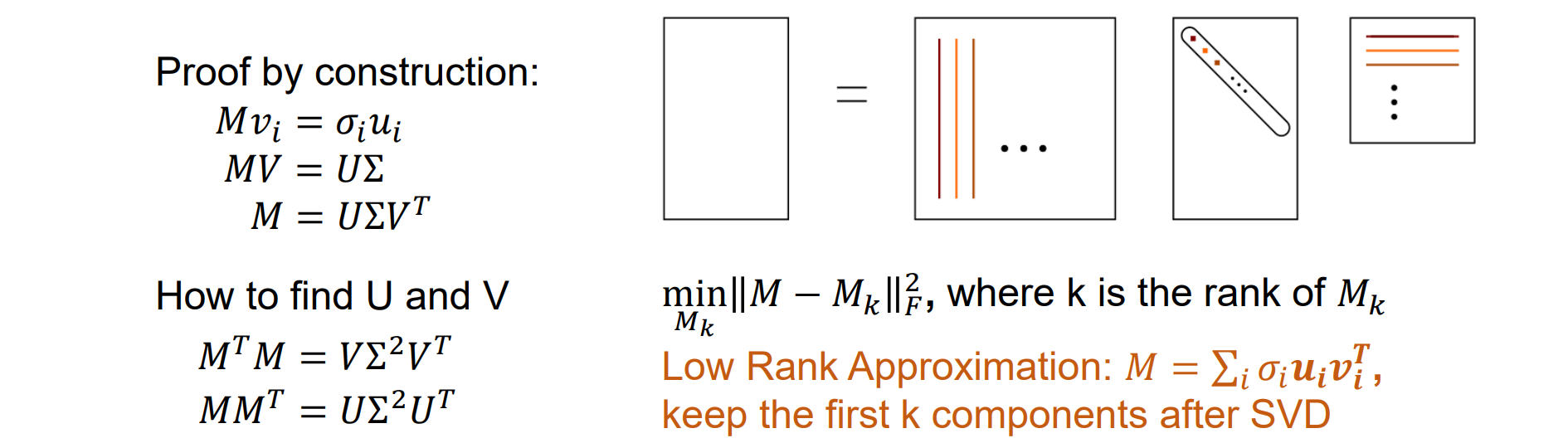
image.png

  • 求得U,V,利用SVD低秩近似，可以只取前K(3)个大的奇异值，将小的置为0

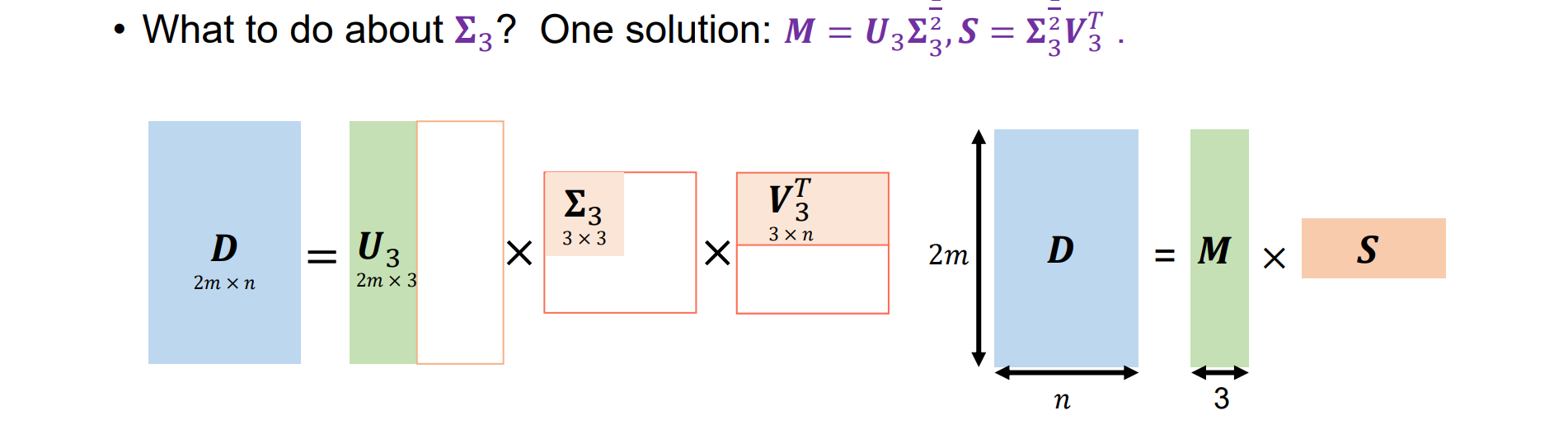
image.png

Eliminating the Affine Ambiguity

  • 加入其他约束可以消除仿射歧义，但仍有其他歧义

  • 添加约束：使每个相机矩阵 AiQ 代表一个正交投影，即具有正交轴（行），即保直角

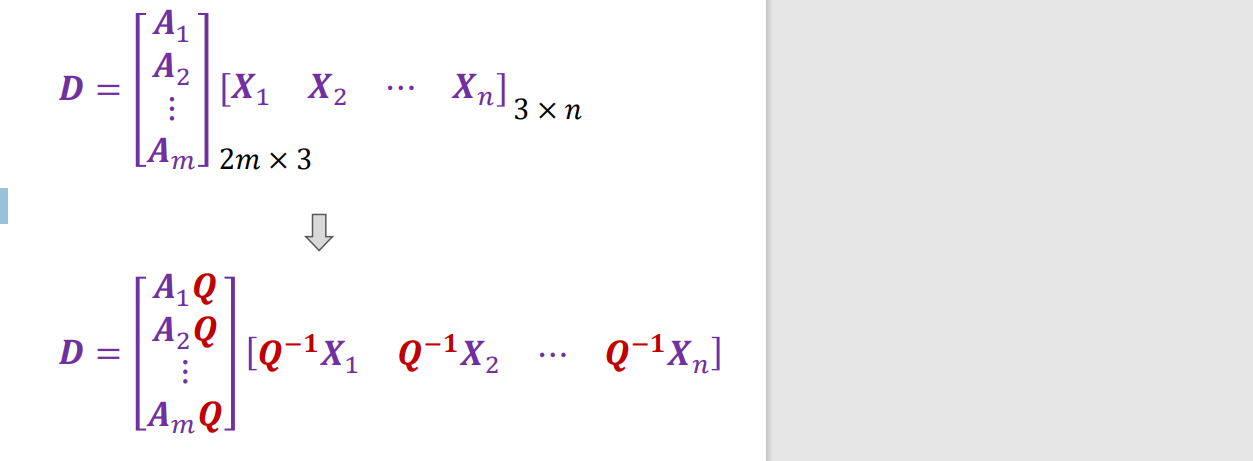
image.png

  • 设 a1 和 a2 是 2 × 3 正交投影矩阵的行：通过投影轴正交可得m个约束，从而使Q变得唯一可解

image.png

  • 但是限制并非是线性的，所以需要设L = QQ.T得到关于L的等式且L是线性的。可以通过最小二乘法的到L，然后再通过Cholesky分解得到Q

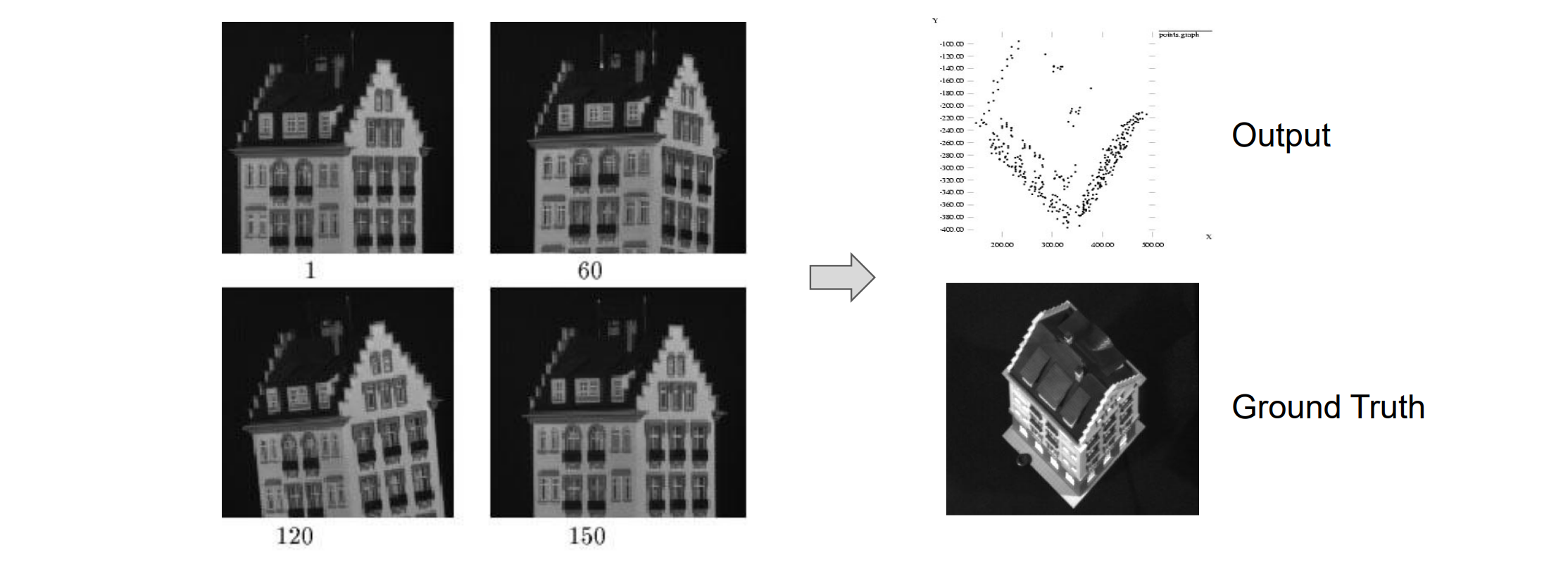
image.png

Dealing with Missing Data

  • 到目前为止，我们假设所有点在所有视图中都可见

  • 实际上，测量矩阵通常如下所示：由于有遮挡，是稀疏的，不可能看到所有点

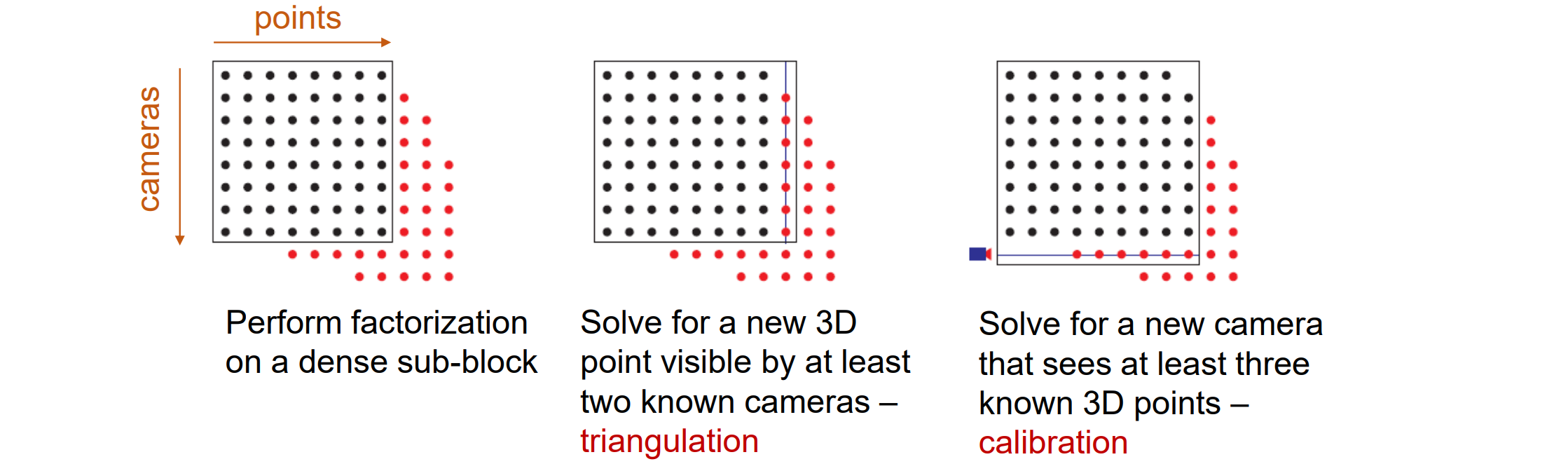
image.png

  • 可能的解决方案：将矩阵分解为密集的子块，分解每个子块，并融合结果，逐块求解。然而在现实中却行不通

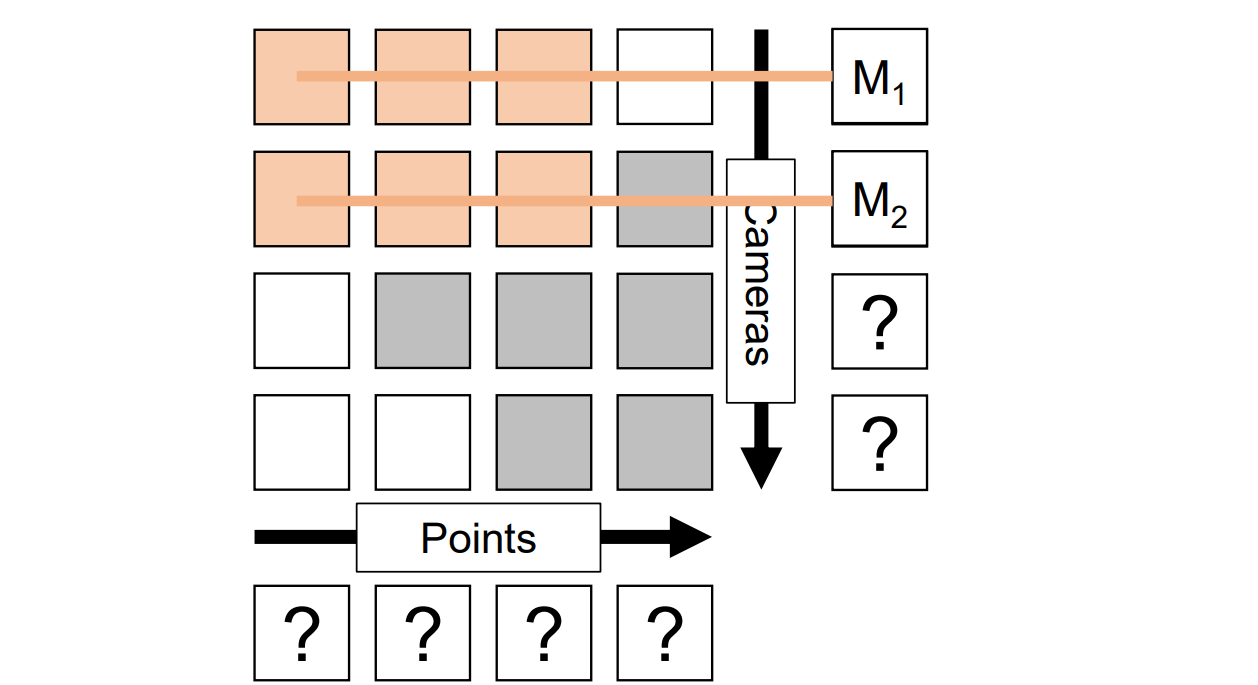
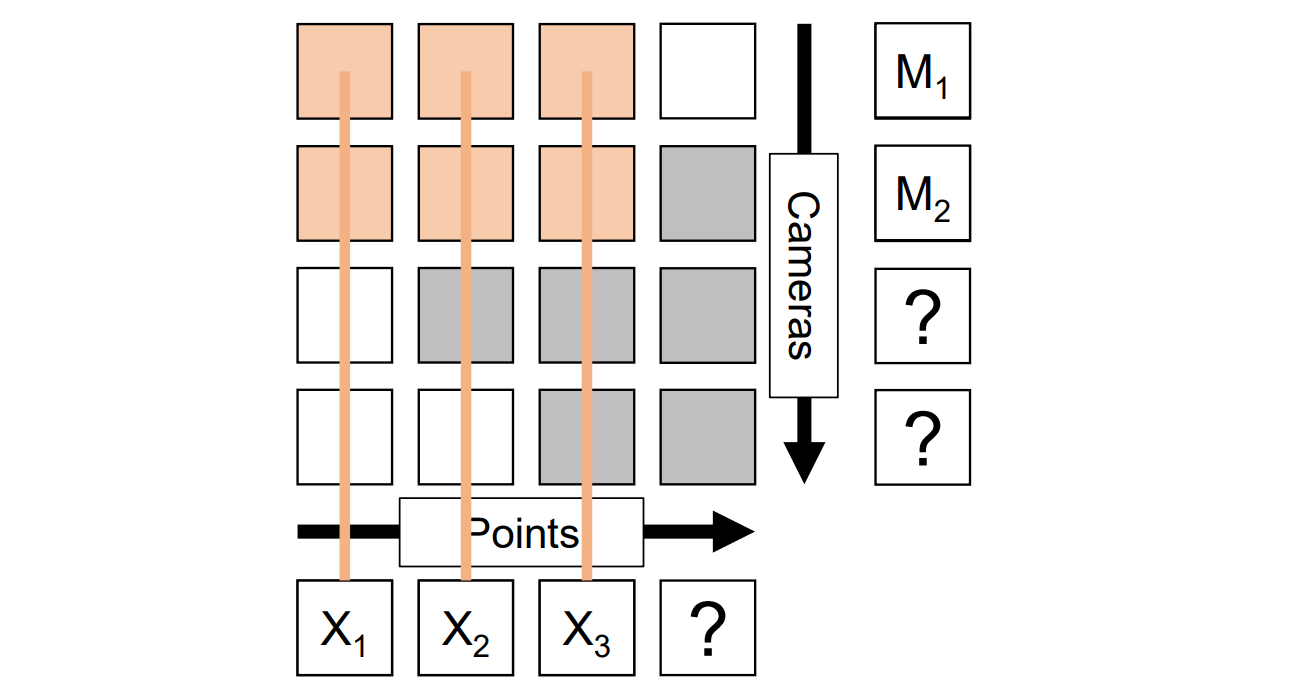
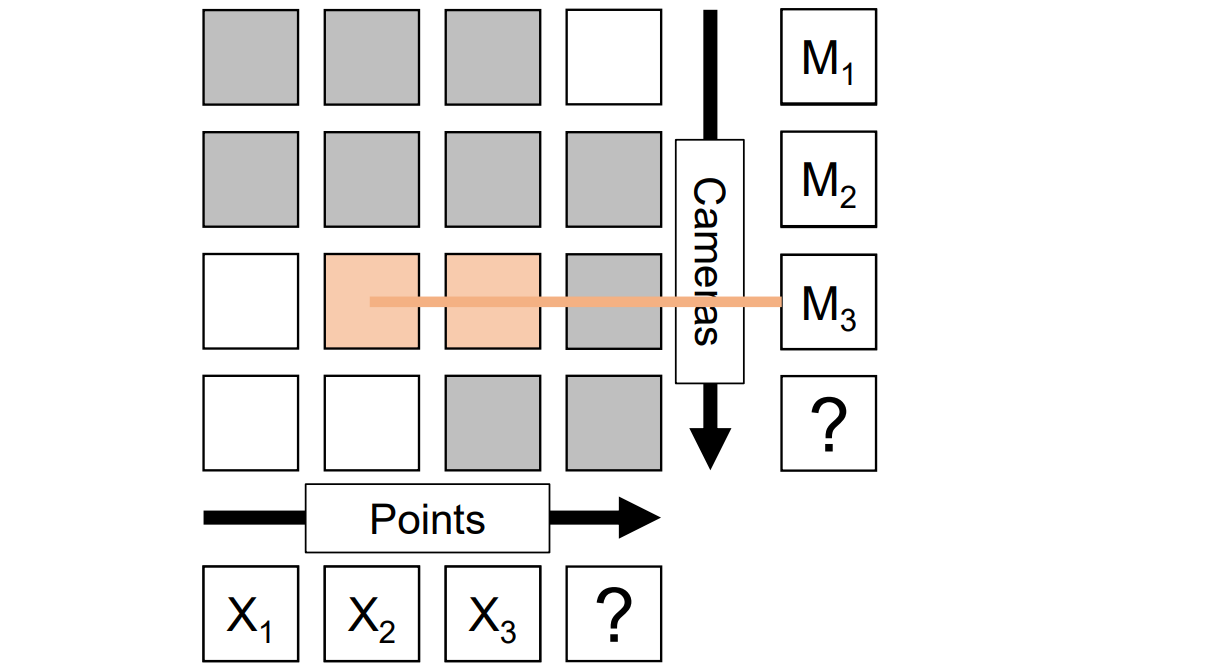
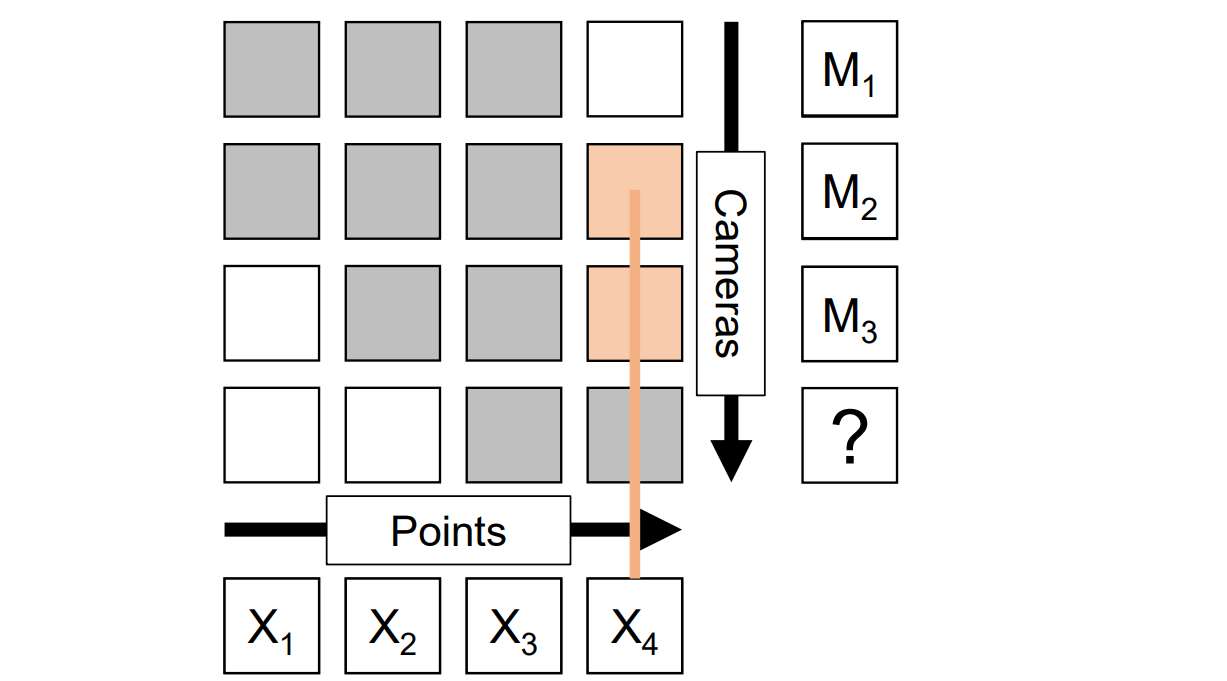
  • 增量法(Incremental bilinear refinement):先求解，求解完后向右拓展一列以解决新的3D点，通过triangulation求解；再向下拓展一行以解决新的相机校准，用calibration求解，然后重复迭代此过程

image.png

Projective Structure from Motion(宽松条件下求解SFM)

  • n 个固定 3D 点的 m 张图像，使得（忽略可见性）：

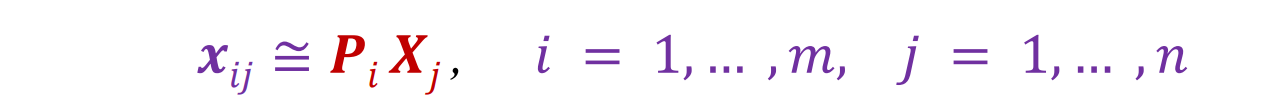
image.png

  • 问题：根据 mn 对应关系 Xij 估计 m 个投影矩阵 Pi 和 n 个 3D 点 Xj

  • 在没有校准信息的情况下，相机和点最多只能恢复 4 × 4 投影变换Q,Q是一族解

  • 2𝑚𝑛 ≥ 11𝑚 + 3𝑛 − 15时可解，对于两个相机，至少需要7个点

Projective SFM: Two-Camera Case

  • 流程：
    1. 使用归一化八点算法(normalized eight-point algorithm)估计两个视图之间的基本矩阵 F
    2. 将第一个相机矩阵设置为 [I | 0]
    3. 然后第二个相机矩阵由 [A | t] 给出，其中 t 是极点 （F.Tt = 0），A = −[t × ]F

Cameras from the Fundamental Matrix

image.png

  • 上述过程为基础矩阵的另一种定义方式。F与H无关，H是另一个投影矩阵

  • 任务转化为：从F中分解A,b

image.png

Self-calibration

  • 自校准是从透视（或仿射）重建中恢复度量重建的问题

  • 可以通过对相机或者世界坐标系假设来消除歧义性完成自校准

ncremental Structure from Motion

Incremental SFM

  • 核心思想：增量地增加相机的3D点

  • 流程：

    1. 使用基础矩阵初始化相机参数 Mi = [Ri ，ti]
    2. 使用Triangulation初始化3D点Xj
    3. 再使用校准和可见的已知点求解相机矩阵，用3D点和2D点匹配可得一个新的相机
    4. 增量式的重复上述过程

image.png

image.png

image.png

image.png

  • 问题：没有考虑3D点和相机放在一个整体进行优化

Bundle Adjustment

  • 用于调整3D点和相机的非线性方法(更新P,X)：最小化重投影误差。其中，wij代表可见性，0代表不可见；1代表可见

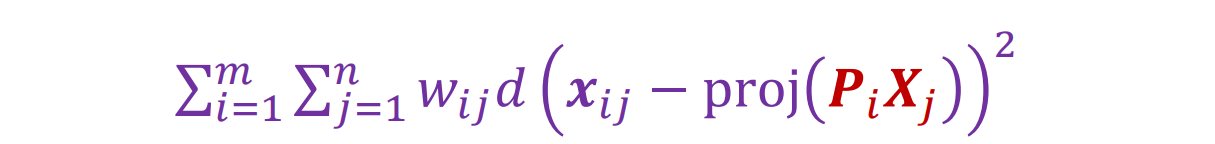
image.png

Photo Tourism: a Representative SFM Pipeline

Feature Detection

  • Detect SIFT features,Other popular features: SURF, ORB, BRISK, …

Feature Matching

  • 使用近似最近邻匹配来匹配每对影像之间的特征(高维空间上的最近邻插值)

  • 使用 RANSAC 通过归一化八点法估计每对之间的基矩阵

Incremental SFM

  • 选择一对具有大量内部值的图像（最好是 EXIF 数据）

    1. 从 EXIF 初始化内部参数（焦距、主点）
    2. 使用五点算法估计外部参数（R 和 t）
    3. 使用三角测量初始化模型点

  • 当剩余图像存在时

    1. 查找与模型中的图像具有许多特征匹配的图像
    2. 对特征匹配运行 RANSAC 以将新图像注册到模型
    3. 三角测量新点
    4. 执行bundle adjustment平差以定期重新优化所有内容
    5. （可选）与 EXIF 数据或地面控制点的 GPS 对齐