Introduction to Recognition

  • Recognition：从图像中重建语义

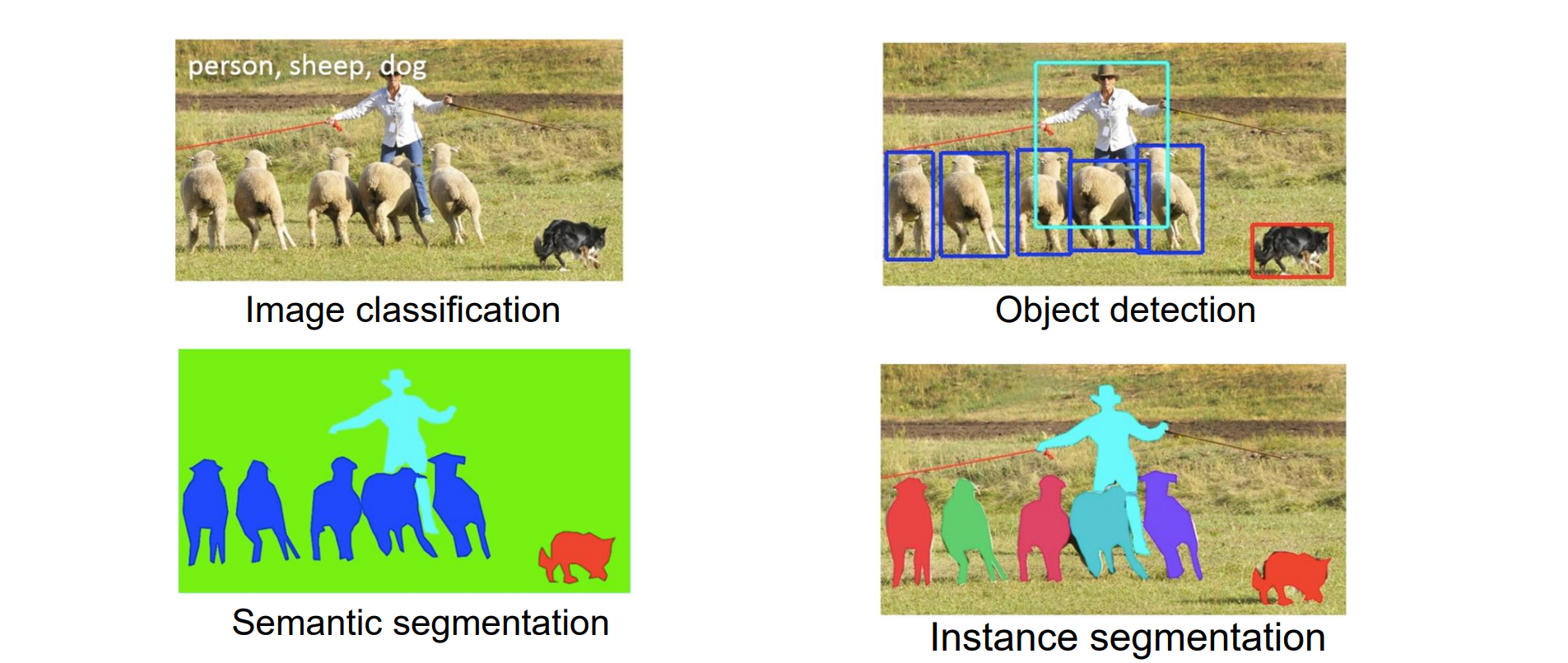
image.png

  • Challenges: Semantic Gap(语义鸿沟)

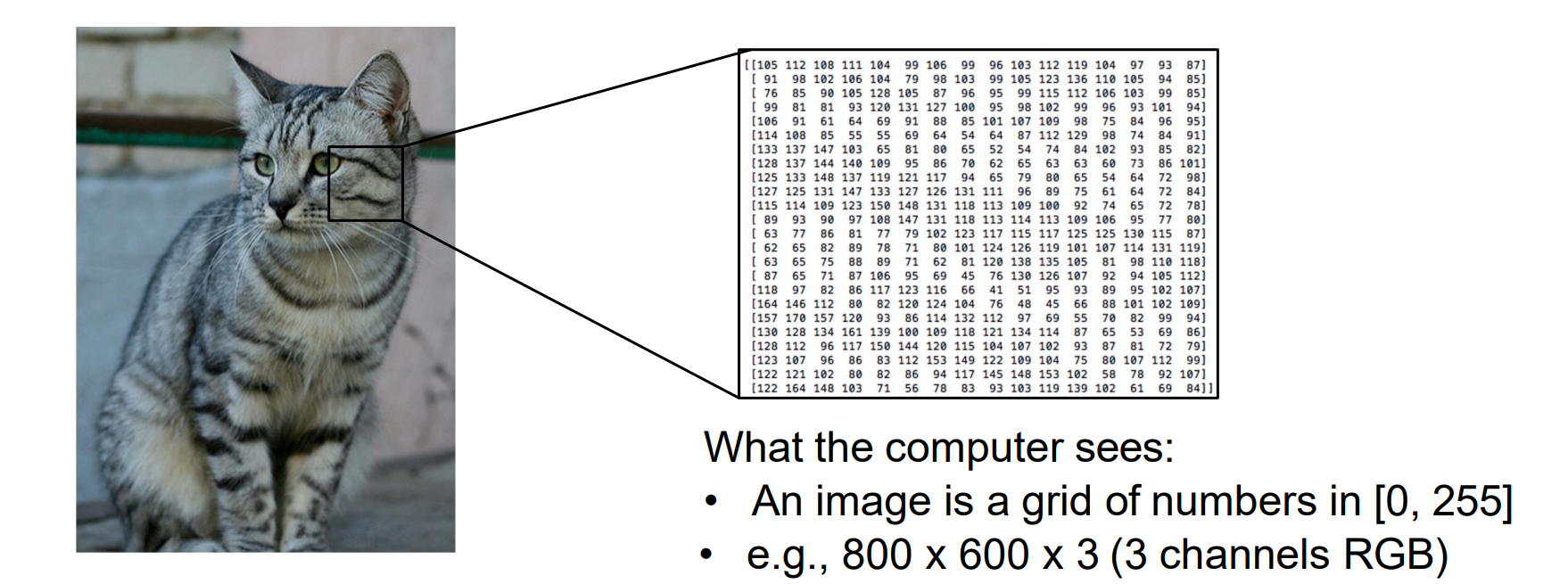
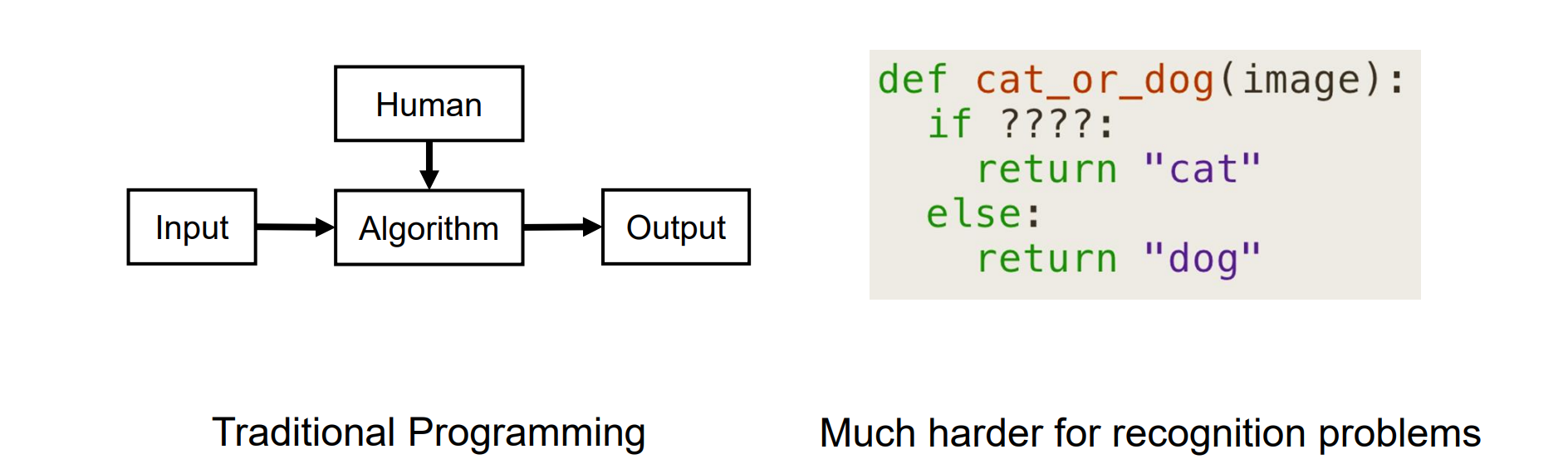
image.png

  • 从图像中重建语义，传统编程可能不使用：image可能有遮挡，并且模式不好找

image.png

  • Learn Semantics from Data：训练是隐式的，让神经网络学习某种准则，完成输入到输出的映射

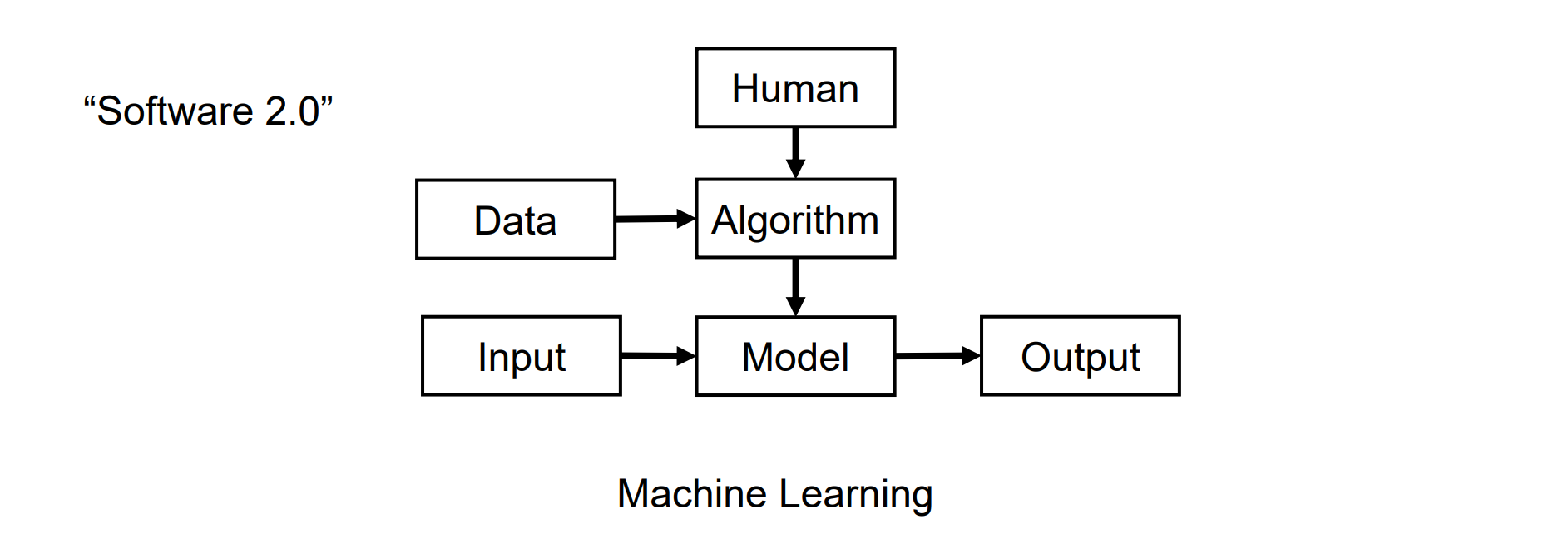
image.png

  • 输入：图像，标签

image.png

  • 有监督学习：有x有y，目的是学习一个从x到y的函数映射。可以分为两类：
    1. 分类问题：预测种类，结果是离散的
    2. 回归问题：从图像中预测连续的值

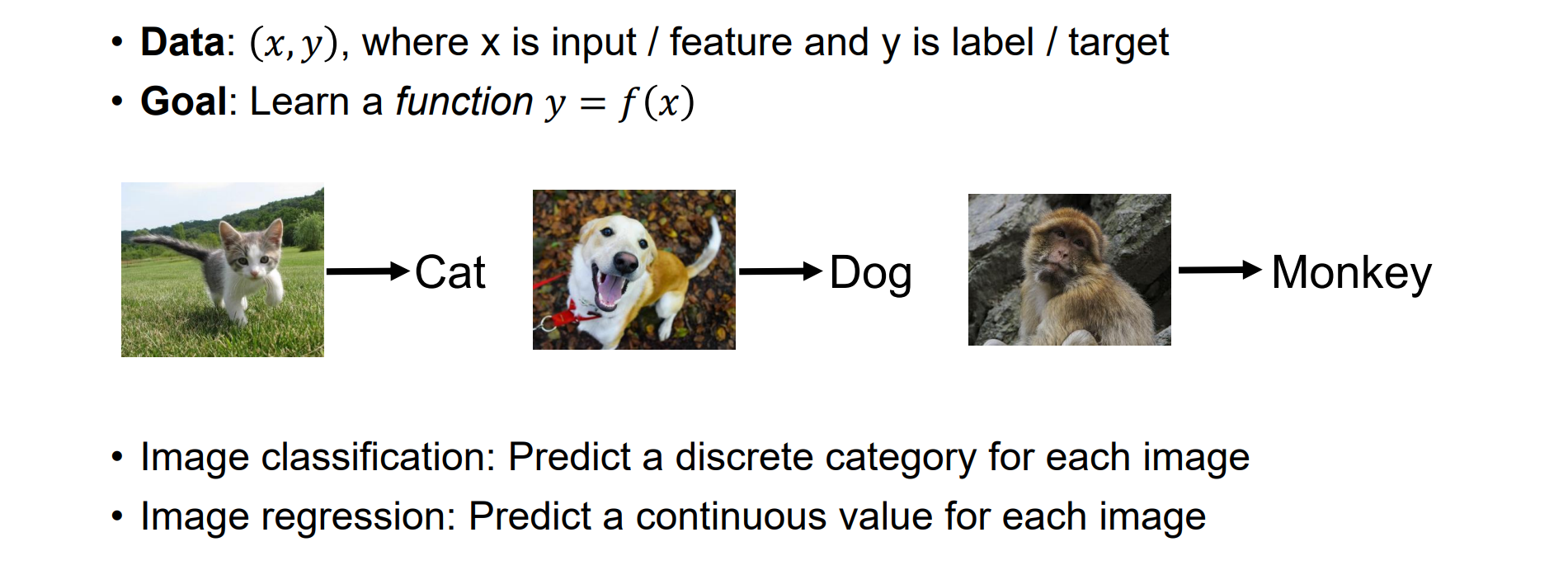
image.png

  • 无监督学习：有x无y，目的是了解数据中重要的基础结构或者分布

image.png

Linear Regression Model

Linear Regression

  • 总思想：线性回归，最小二乘求解。给定数据data，定义模型并写成点乘形式，定义损失函数。然后拟合误差，使得argmin(Loss(x))，即为训练过程

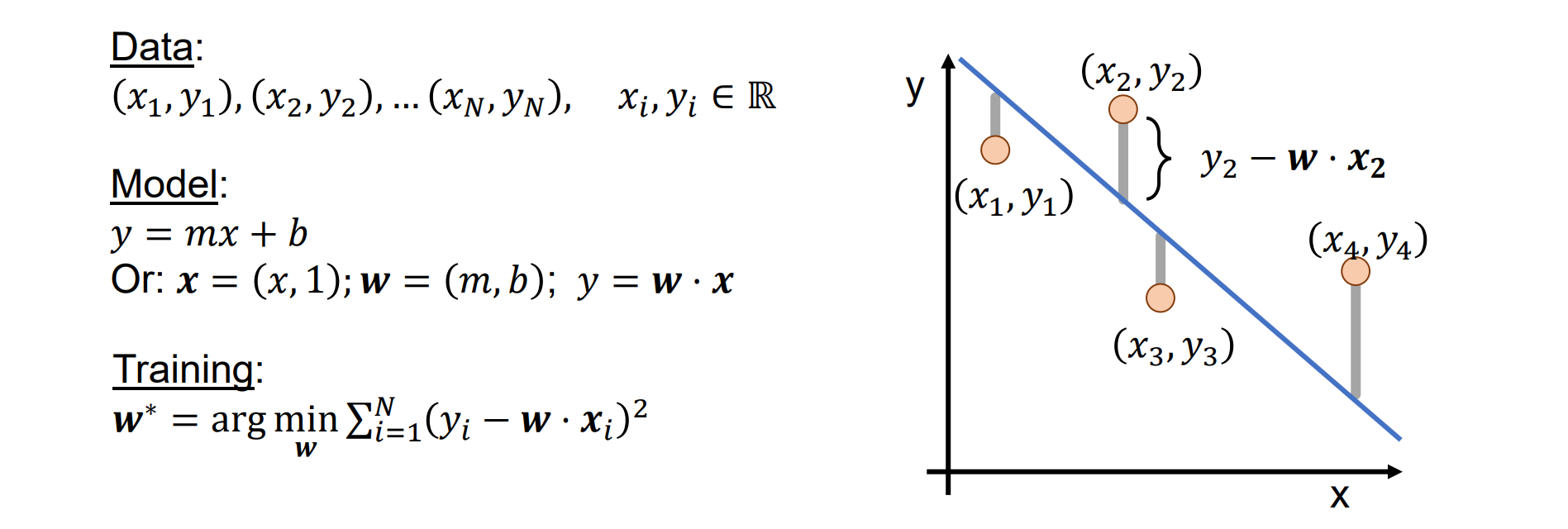
image.png

Solve Linear Regression with Least Squares

image.png

  • 问题：我们不太关心训练集的性能;我们想知道模型如何泛化到新数据。模型在训练集上表现很好，但是推广能力比较差

  • 解决方法：将数据集拆分为训练集(train sets)和测试集(test sets)。拟合 train set，并在两个集合上求值

Overfitting and Regularization

  • 问题：过拟合，在训练集上误差很小但是在测试集上误差很大，说明不能很好的泛化到新的数据中

  • 产生原因：从传统观念来看，过拟合是拟合到了训练集中的噪音

  • 从传统机器学习的角度来看，过于灵活的模型很容易过度拟合

  • 解决方法：正则化，权重衰减(weight decay)是一种常用的正则化策略

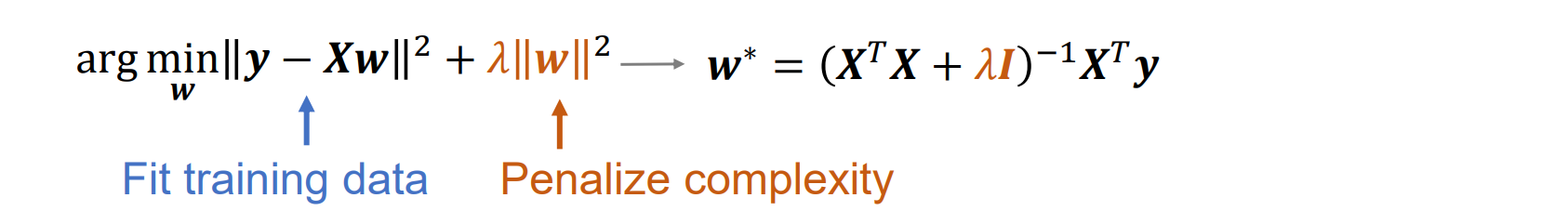
image.png

  • λ的几种情况：
    1. λ=0，没有正则化，模型过拟合
    2. λ=0.1，此时λ太大会导致欠拟合：该模型与训练数据拟合不佳，训练和测试数据都存在很大的误差。模型不够灵活

Parameters and Hyperparameters

  • 参数（w）：在训练期间通过拟合训练数据进行优化

  • 超参数（λ）：在训练之前选择，不依赖于训练数据

Choosing Hyperparameters

  • idea #1：选择在整个数据集上效果最好的超参数。BAD：λ = 0 对训练数据效果最佳

  • idea #2：将数据拆分为训练和测试;选择最适合测试数据的超参数。BAD：不知道处理新数据表现如何，泛化能力低

  • idea #3：将数据拆分为 train、val 和 test;选择 Val 上的 Hyperparameters 并且测试数据评估

  • idea #4: Cross-Validation:将数据拆分为folds，尝试将每个folds作为验证并平均结果。对于小型数据集很有用，但在深度学习中使用频率不高

image.png

多维输入线性回归

image.png

多维输入输出线性回归

image.png

  • 仍然可以用最小二乘法求解

Summary:

  • 机器学习是一种数据驱动编程形式：

    1. 有监督学习将输入映射到输出
    2. 无监督学习在没有标签的数据中找到一种结构和模式

  • 最小二乘线性回归：

    1. 正则化可以控制过拟合和欠拟合
    2. 使用训练集查找最佳参数
    3. 使用验证集选择超参数
    4. 使用测试集一次来估计泛化水平

Linear Classifier

  • 输入：照片；输出：类别

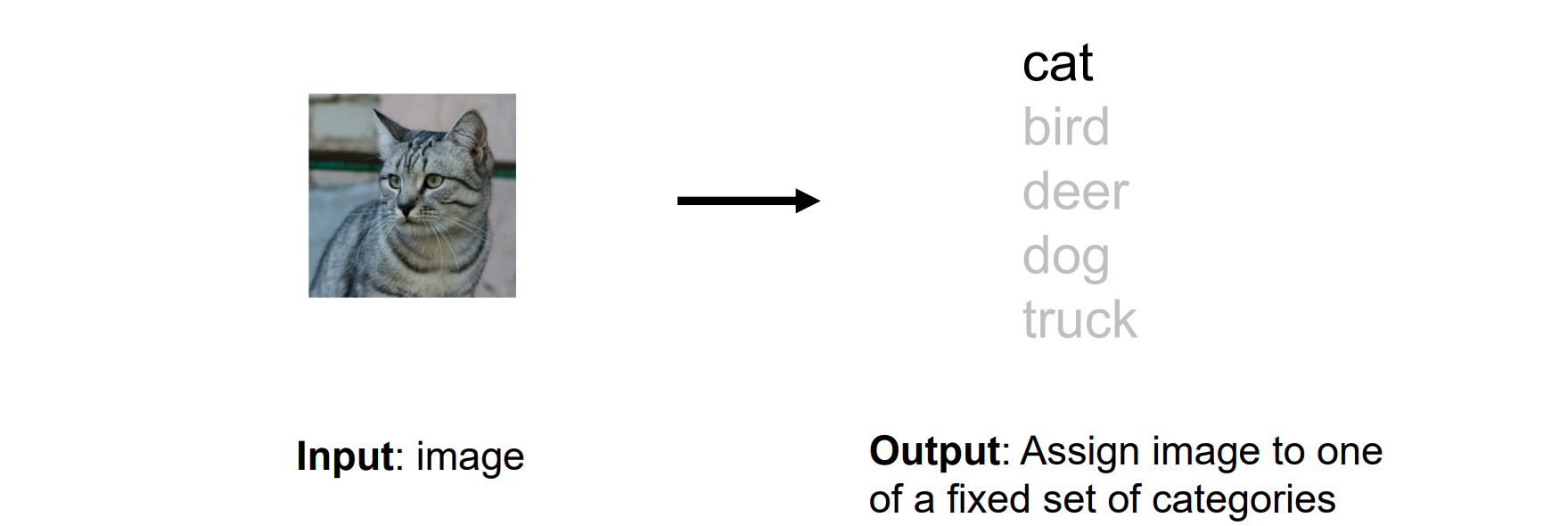
image.png

  • 分类问题必须使用one-hot独热编码：映射到高维空间，每一维是0或1

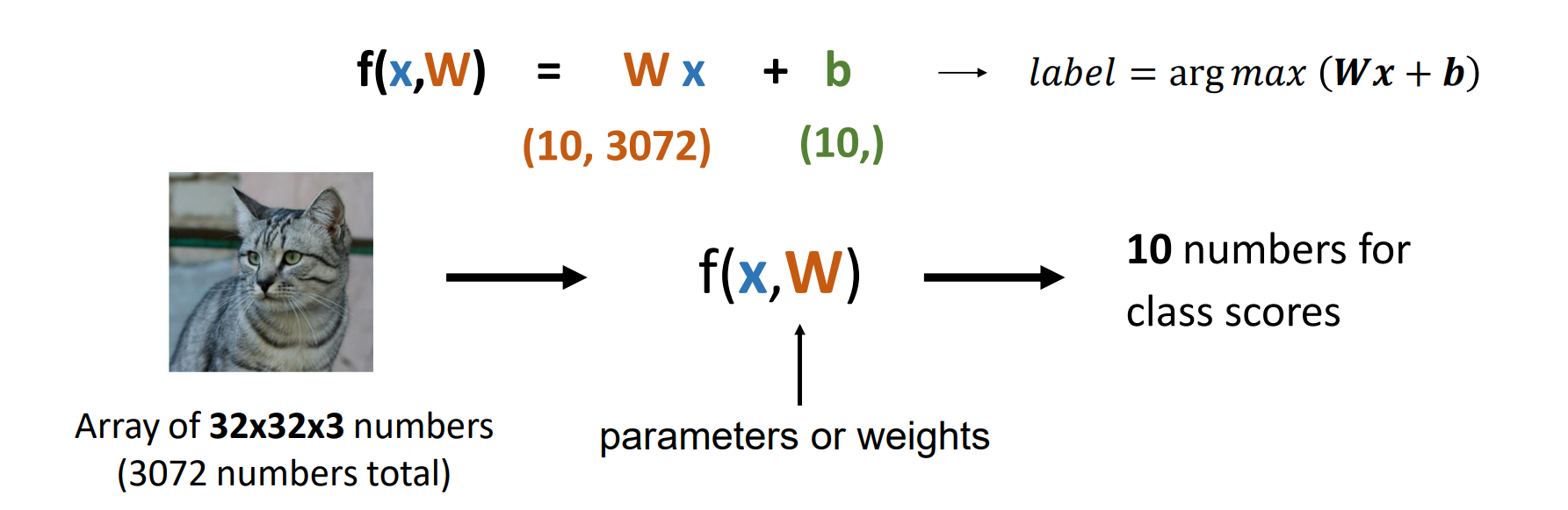
image.png

Linear Classifier: #1 Algebraic Viewpoint(代数观点)

  • 将b拼到w右侧形成一个大矩阵，点成输入图像矩阵看哪行点乘最大

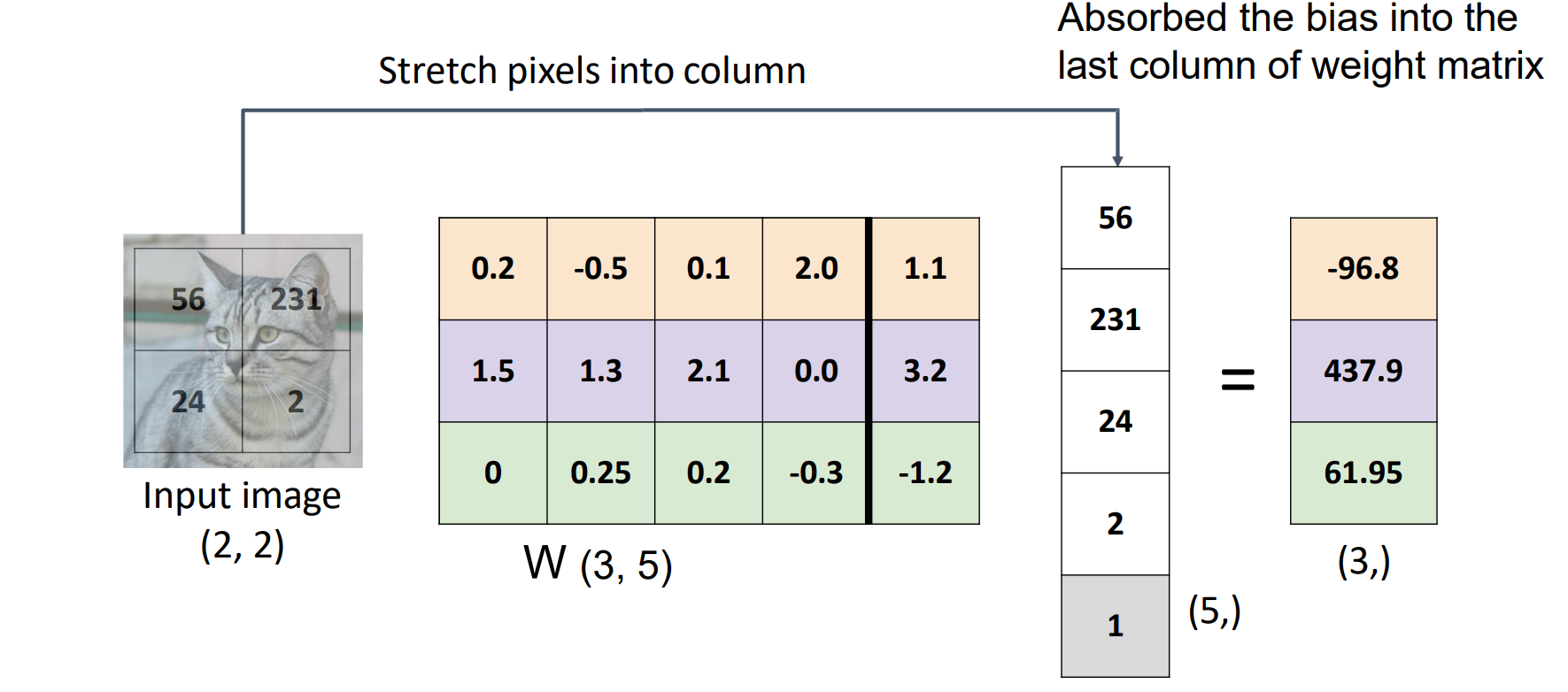
image.png

Linear Classifier: #2 Visual Viewpoint

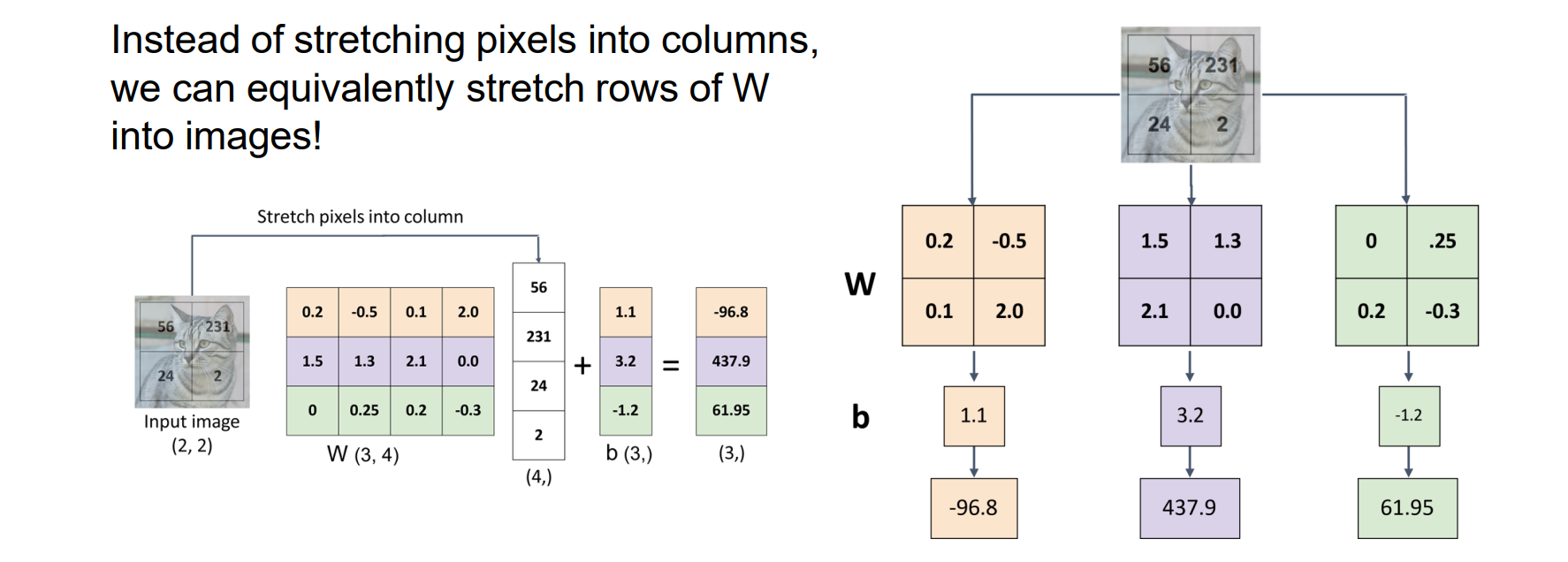
  • 等效地将W行拉伸到图像中，而不是将像素拉伸成列

  • 将w换成图像形状点乘看相关性，有点类似于模板匹配

image.png

Linear Classifier: #3 Geometric Viewpoint(几何观点)

  • 将输出每行作为线性方程画出，取最高值对应的label

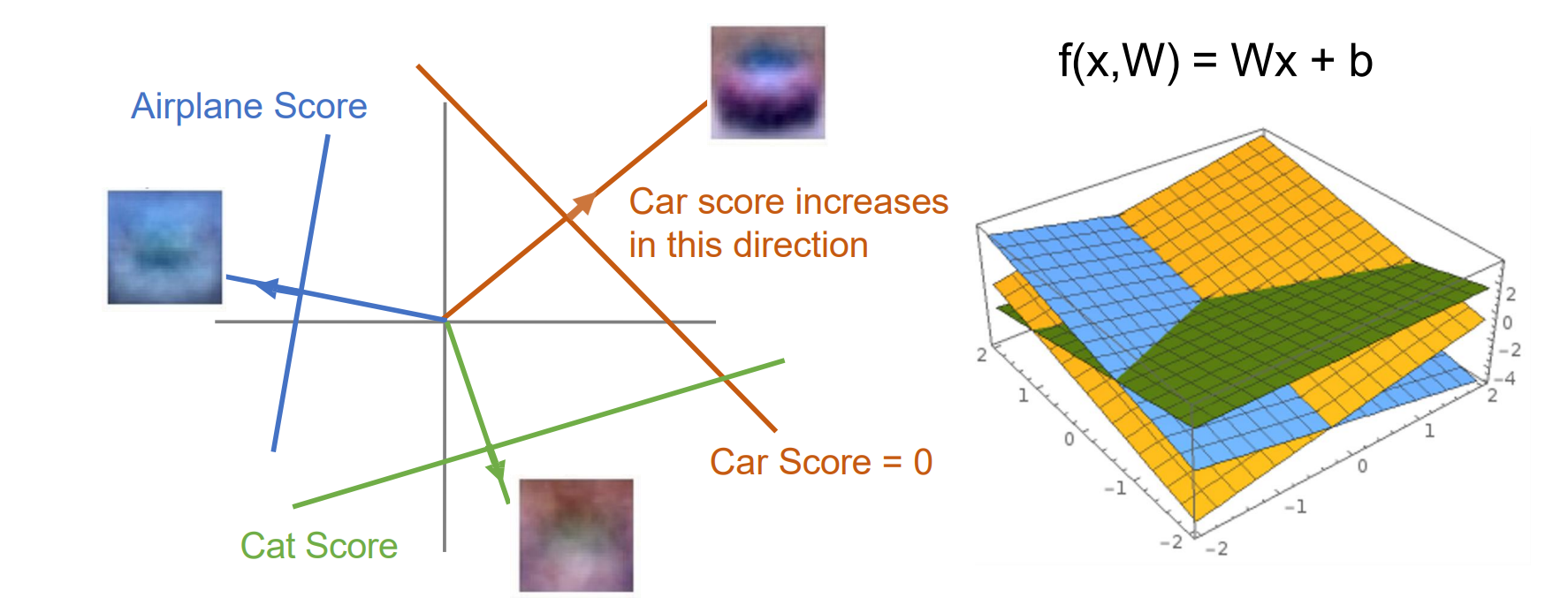
image.png

线性分类的局限性

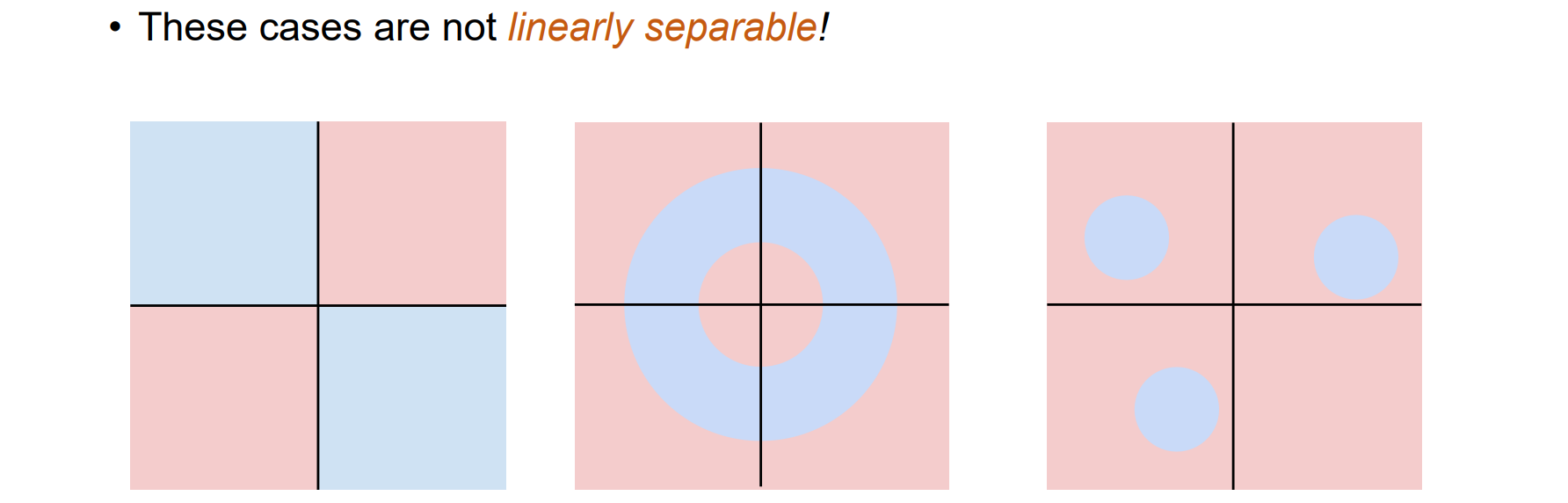
  • 问题：线性不可分问题，例如异或问题，高维划分问题

image.png

Linear Classifier: Three Viewpoints

  • 训练线性分类器时需要一个损失函数来优化

L2 Loss

  • 使用L2损失函数和最小二乘法解决分类问题：使用回归进行分类通常是有效的

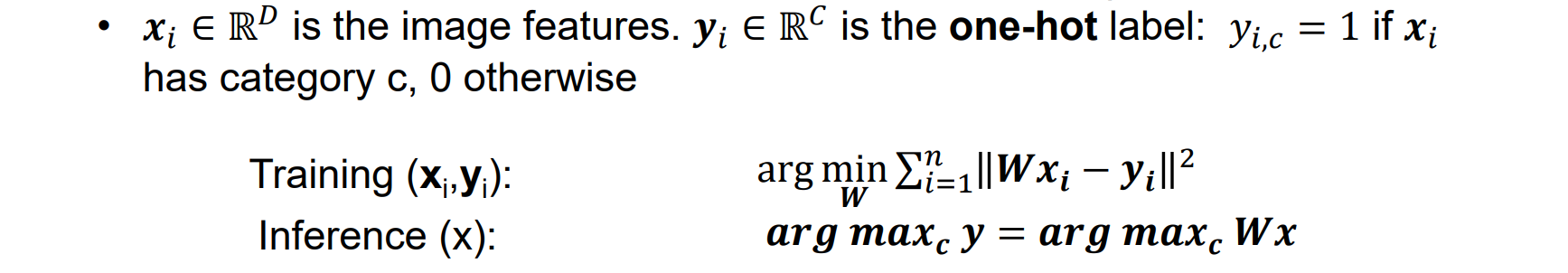
image.png

Cross-Entropy Loss

  • cross-entropy loss：将分类器分数解释为概率并获取交叉熵损失，最大似然估计：选择权重以最大化观测数据的可能性

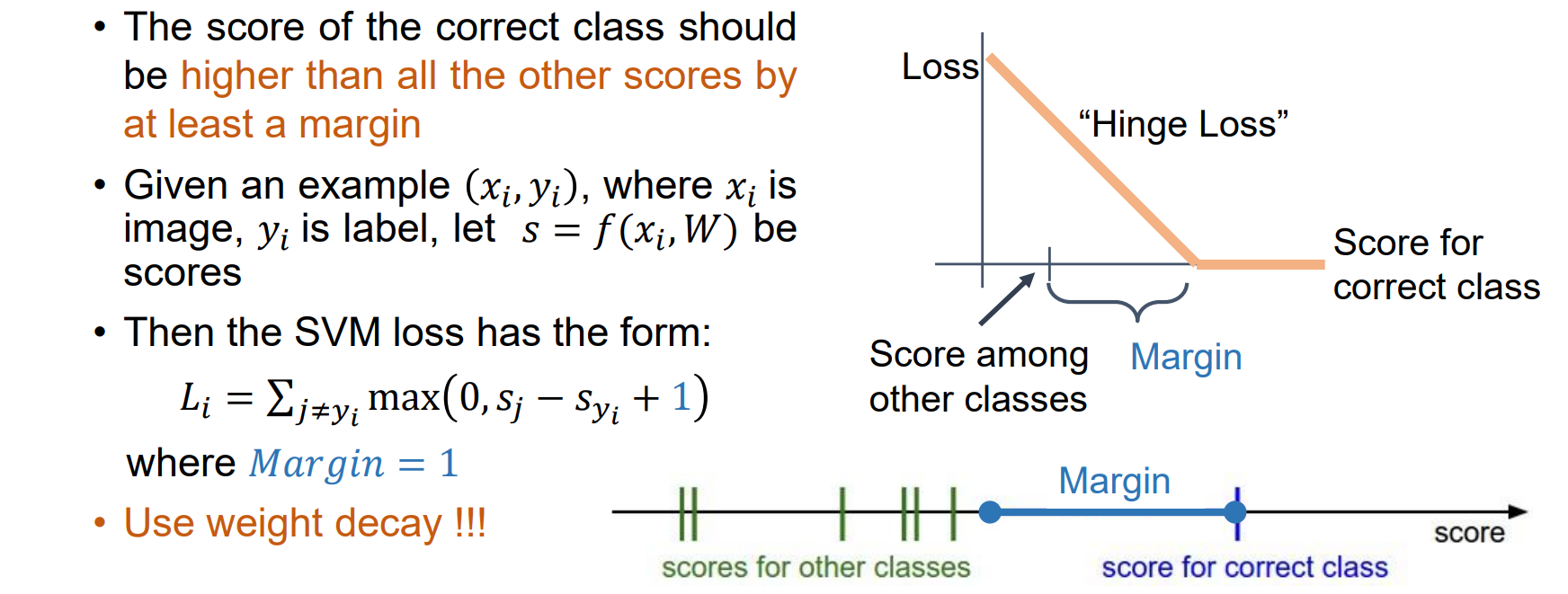
image.png

SVM Loss

  • SVM loss：正确分类的分数应至少比所有其他分数高出一点，否则进行惩罚

  • 需要使用weight decay

image.png

Summary

image.png