Optimization

Optimization with Grid Search

均匀采集样本点，遍历样本点遇到损失值更小的就进行更新

best, bestScore = None, Inf
for d1 in range1:
    for d2 in range2:
        w = [d1, d2]
        if L(w) < bestScore:
            best, bestScore = w, L(w)

优点：简单，只需要评估模型，对函数没有要求
缺点：计算代价高，高维求值困难

Optimization with Random Search

随机采样，与问题维度无关

best, bestScore = None, Inf
for iter in range(numIters):
    w = random(N,1) # sample
    score = 𝐿(𝒘) # evaluate
    if score < bestScore:
        best, bestScore = w, score

优点：简单：只需要评估模型，对函数无要求
缺点：维度高的时候可能因为随机采样点稀疏而错过最优解

When to Use Grid/Random Search

维度低
定义域受限
目标函数难以分析系
Random search与其他策略结合使用时通常更有效，Grid search使系统地测试某些内容变得容易

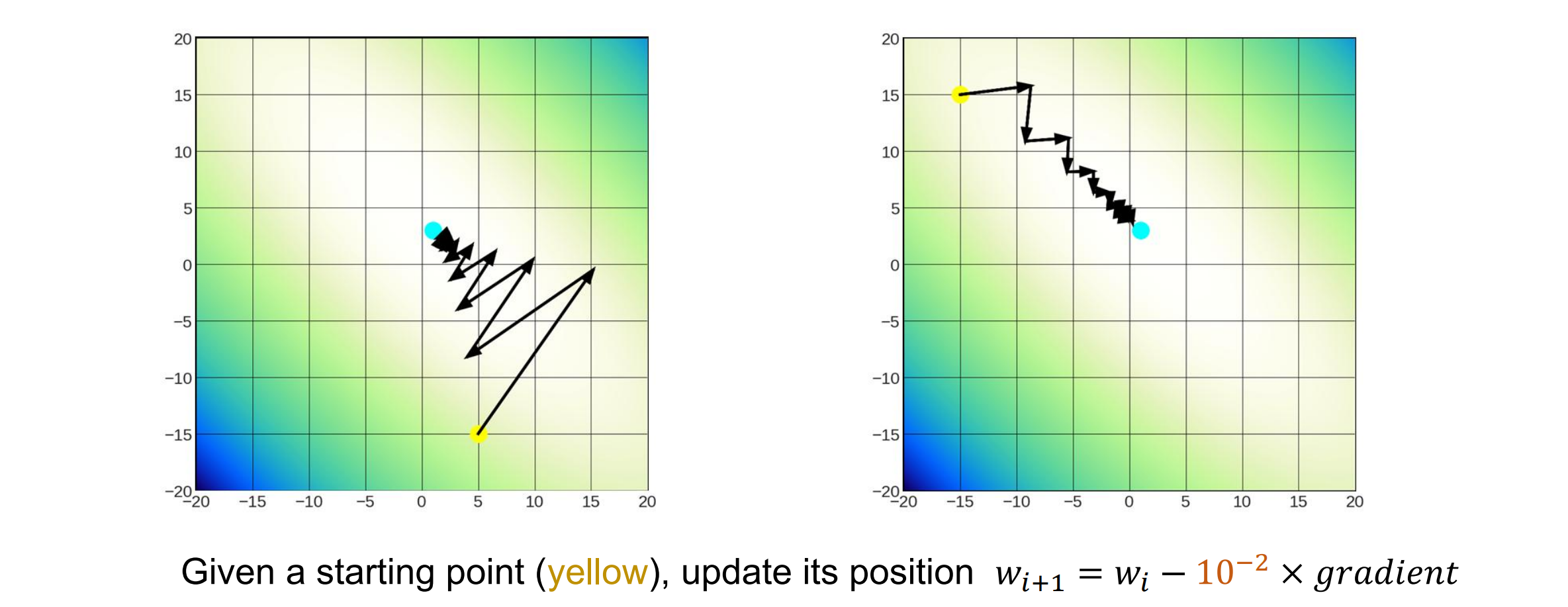
Optimization with Gradient Decent

梯度表示函数最快增长的方向和速率
Gradient Decent：在当前点沿函数的负梯度方向执行重复步骤，以找到函数的（局部）最小值
起始位置随机，不能保证全局最优，只能保证最后的梯度=0，即局部最优

Compute Gradients: Numerical Method(数值方法)

使用有限差分来近似导数，一般使用中心差分准确率最高

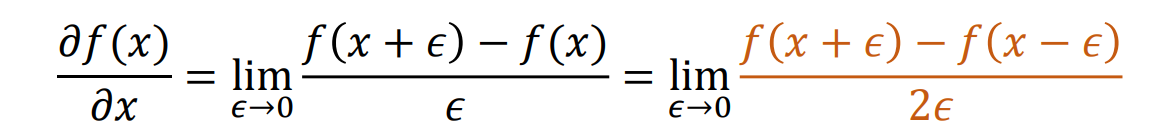
Numerical gradient: approximate, slow, easy to write

Computing Gradients: Analytic Method(解析法)

对于线性回归问题，梯度计算如下：

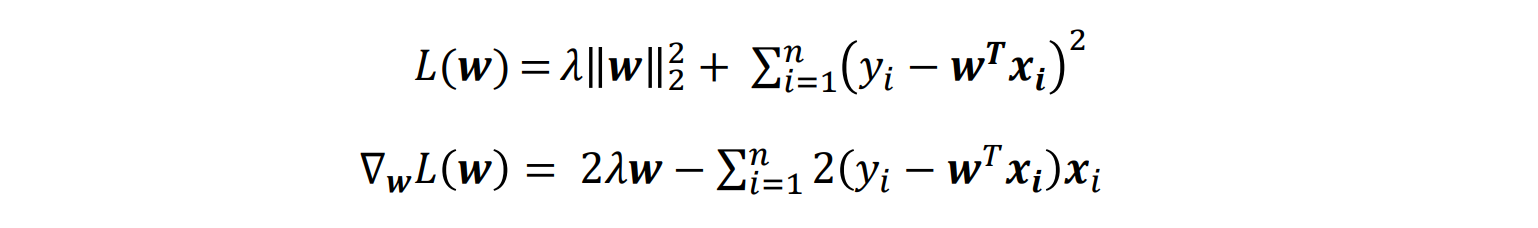
Analytic gradient: exact, fast, error-prone
在使用中通常使用Analytic gradient

Stochastic Gradient Descent: SGD

梯度下降的问题：当 N 很大时，计算总和代价很高

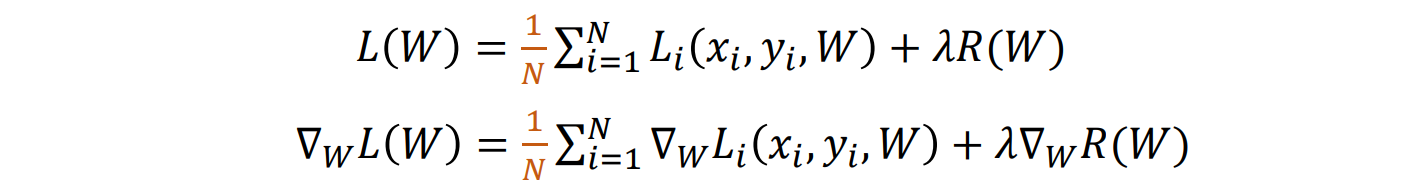
解决方法：蒙特卡洛积分，用minibatch来对N进行逼近

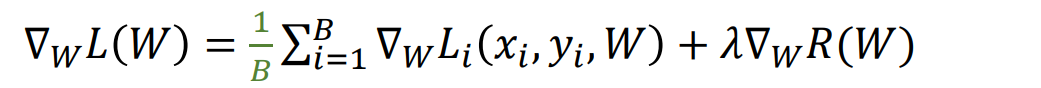
超参数：
1. 迭代步数
2. batch size
3. wight初始化
4. lr

w = initialize_weights()
for t in range(num_steps):
    minibatch = sample_data(data,batch_size)
    dw = compute_gradient(loss_fn,minibatch,w)
    w -= lr * dw

Problems of SGD: #1

目标函数在某一方向变化剧烈在另一方向变化很小。条件数差大的时候，梯度抖动很大

如果减小step size可以减小梯度抖动，但是更新速度会变慢

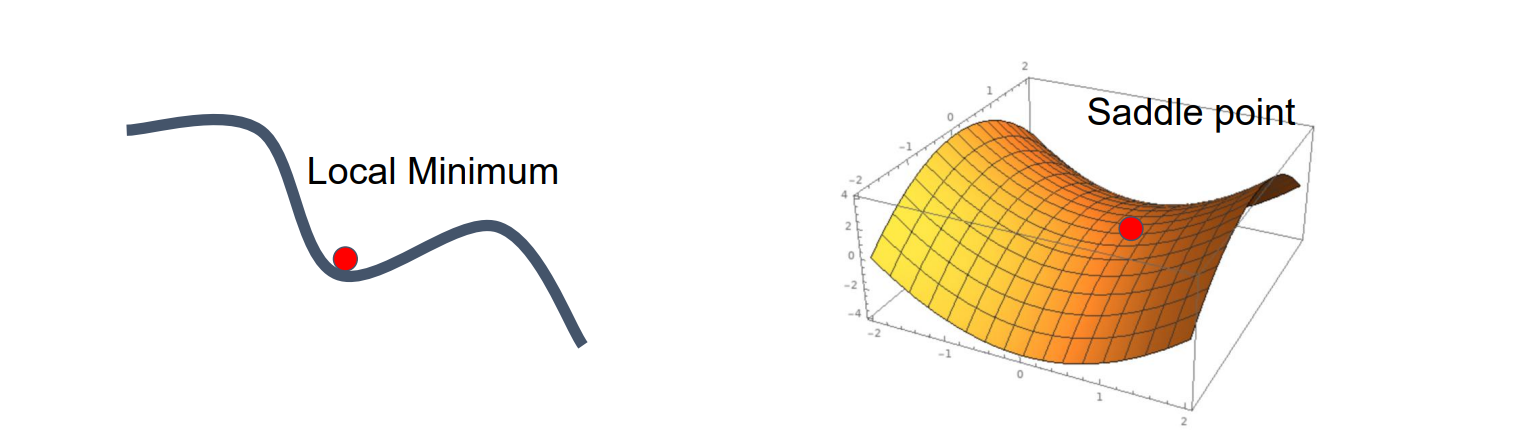
Problems of SGD: #2

难以跳脱局部最小值和鞍点

Problems of SGD: #3

噪声大，如果batch size << total sample number N

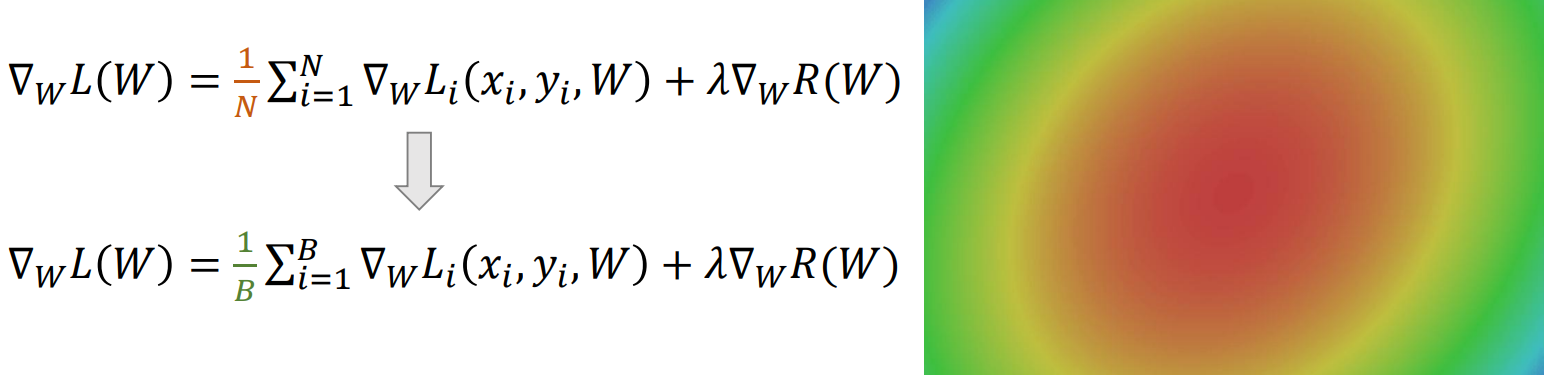
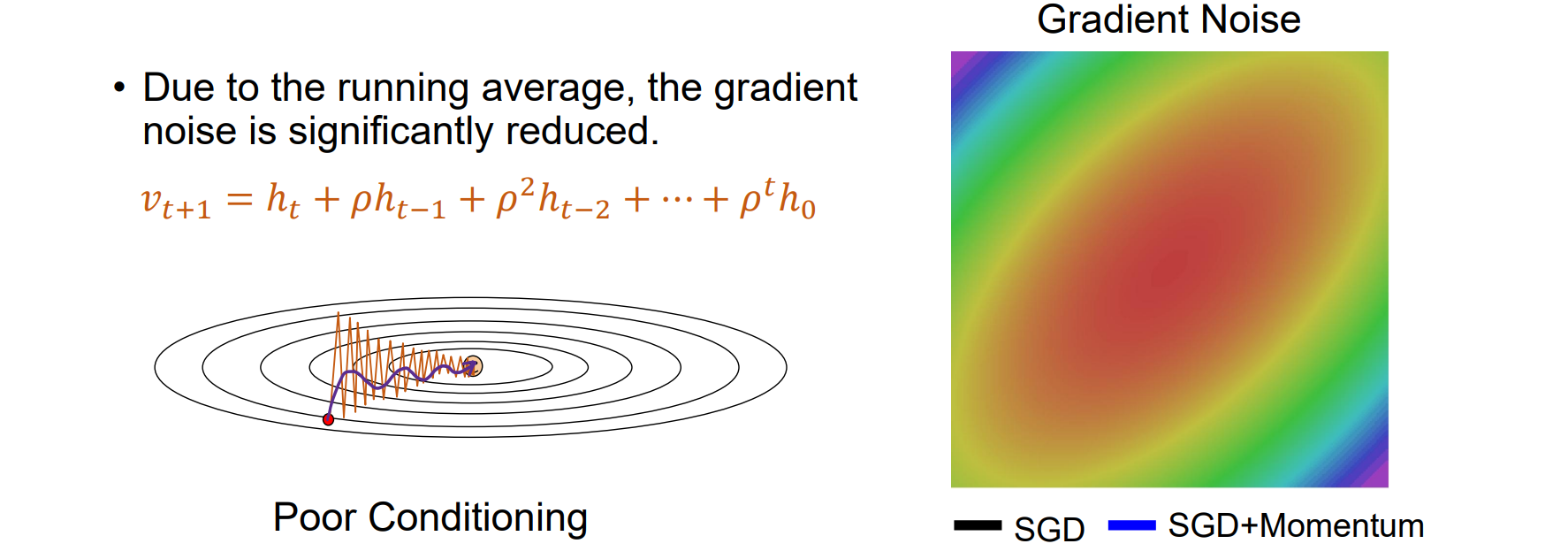
SGD with Momentum

Key idea: Build up the velocity for loss decent as a running mean of gradients，每一次的更新受到历史因素的影响

考虑历史因素在局部最小或者鞍点仍有扰动

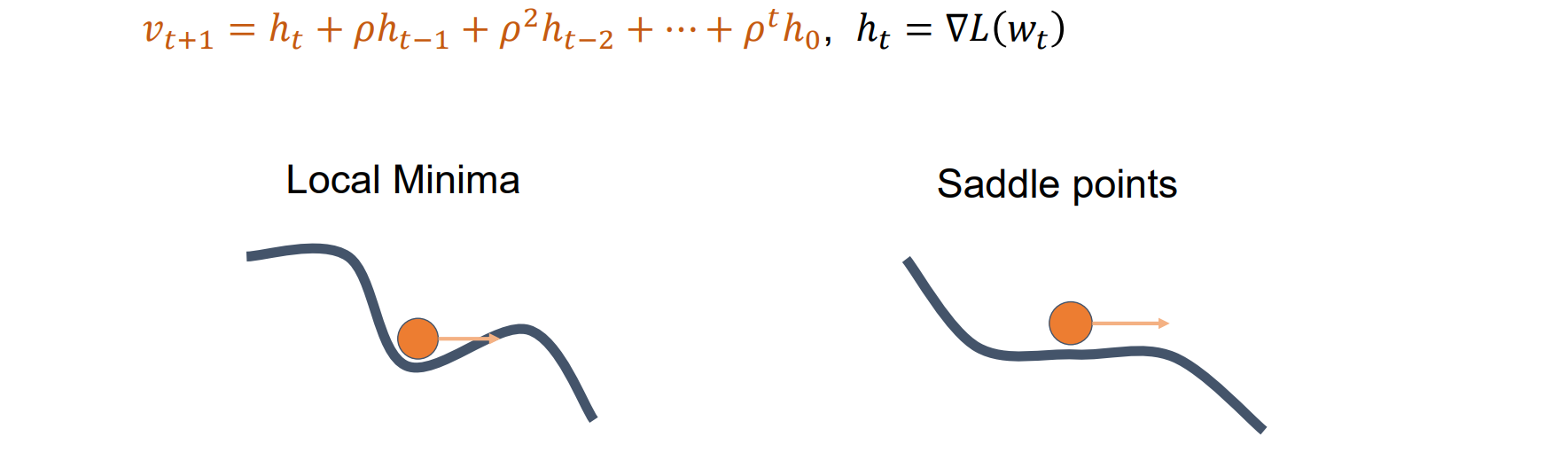
SGD with Momentum抖动小，收敛更快，噪音低

Nesterov Momentum

先按照历史累计的v走一步到A，然后再在A处找梯度下降

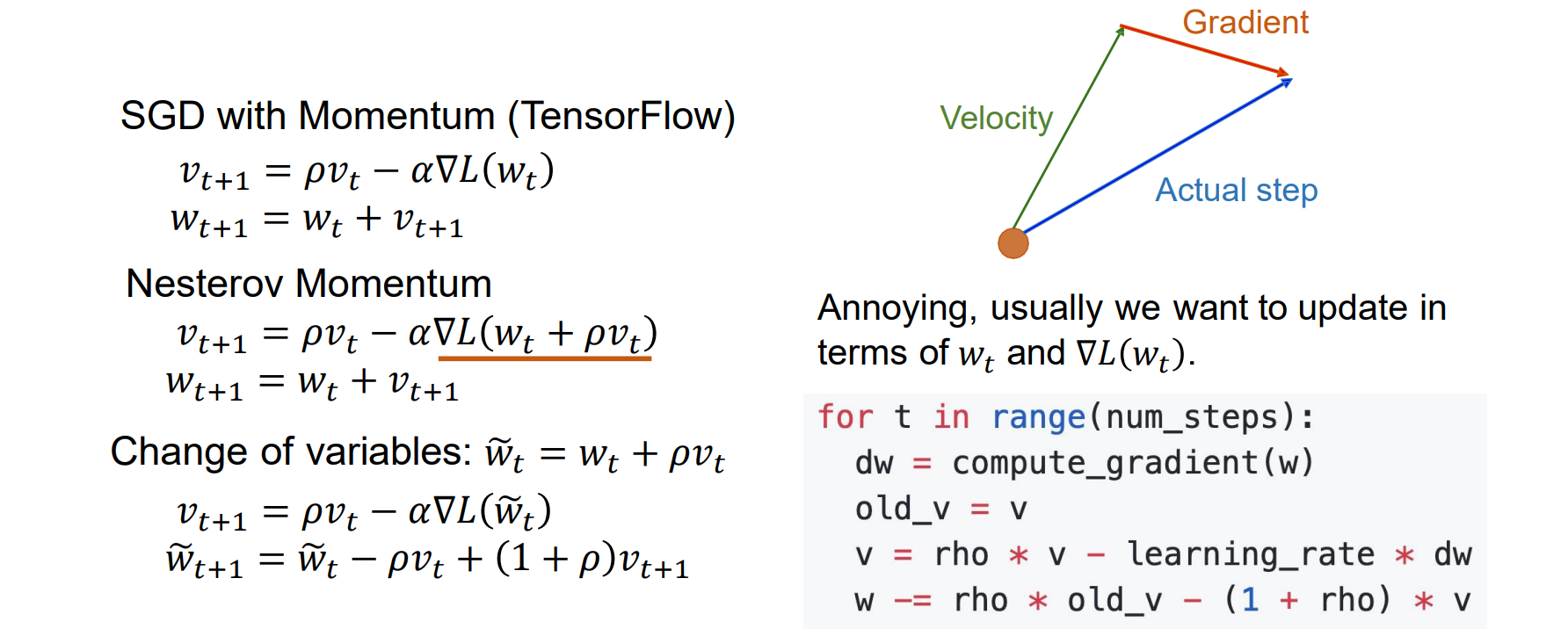
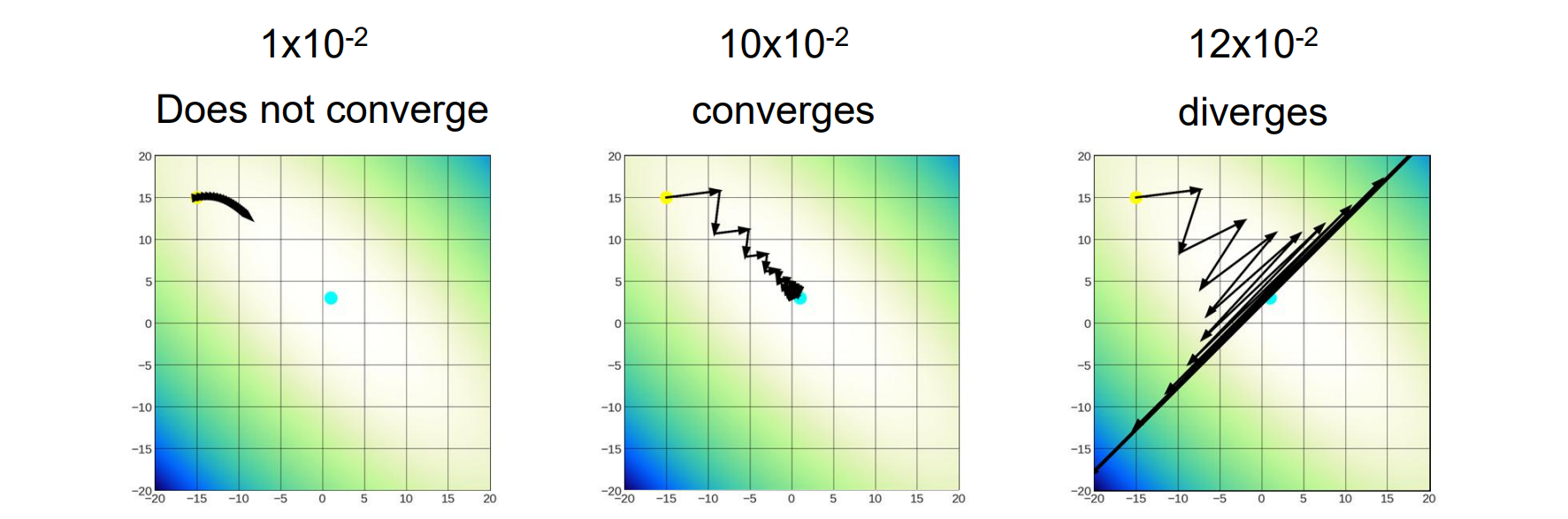
Nesterov Momentum收敛速度更快，但是当lr太高的时候会导致overshooting

Learning Rate

lr是一个重要的超参数：
1. lr太小会导致更新速度太慢
2. lr太大会导致overshooting

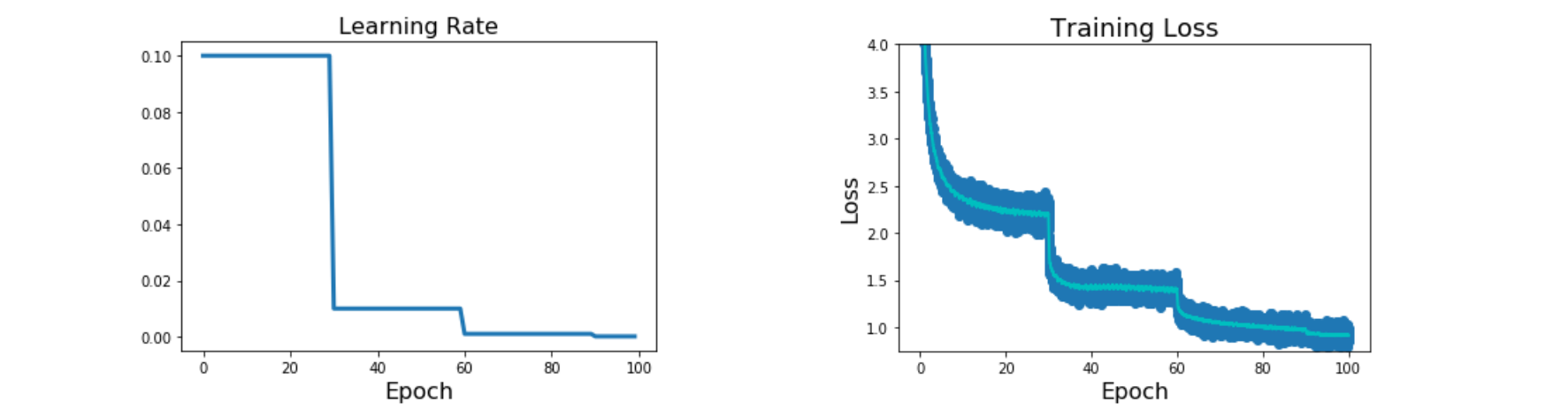
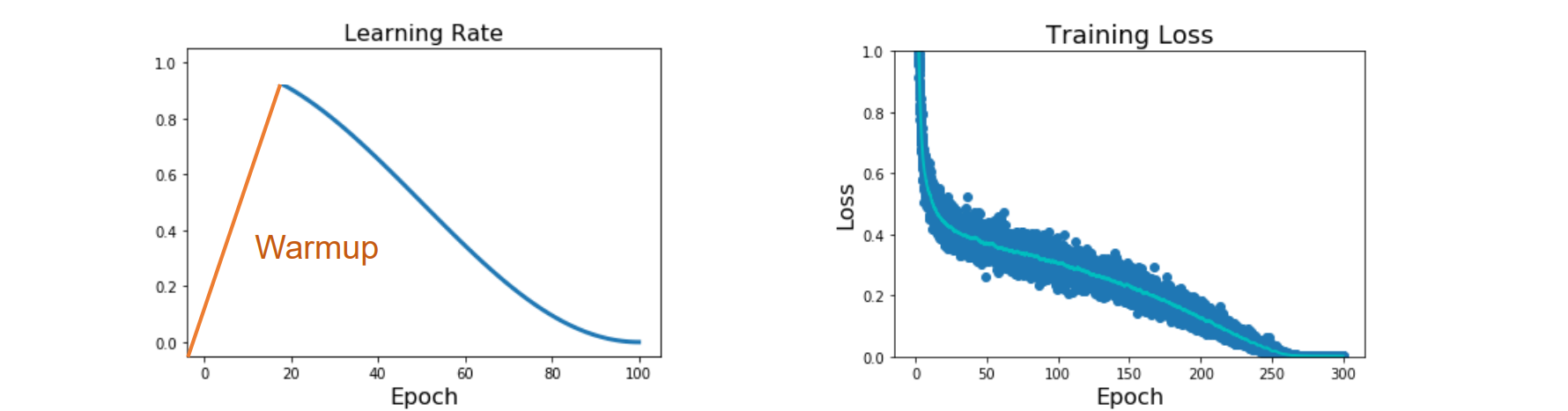
Stepwise Decay

Idea: Start with high learning rate, reduce it over time.Reduce by some factor at fixed iterations
在某个迭代次数后，lr下降

Cosine Decay

Idea: Start with high learning rate, reduce it over time.reduce the learning rate following：

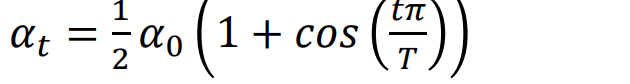
Adaptive Learning Rate Methods

稀疏梯度问题：当参数比较多时，很多梯度约等于0，且样本类出现次数不同，可能有的偶尔被激活，应该应用不同的lr

AdaGrad

调整学习率是一个代价很高的过程;因而希望自适应地调整学习率，甚至按参数进行调整
AdaGrad 根据每个维度中的历史平方和添加了梯度的元素缩放，这适用于稀疏梯度

grad_squard = 0
for t in range(num_steps):
    dw = compute_gradint(w)
    grad_squared += dw * dw
    w -= lr * dw / (grad_squared.sqrt() + 1e-7)

问题：AdaGrad 积累grad_squared，从而不受限制地不断增长

RMSProp: “Leaky Adagrad”

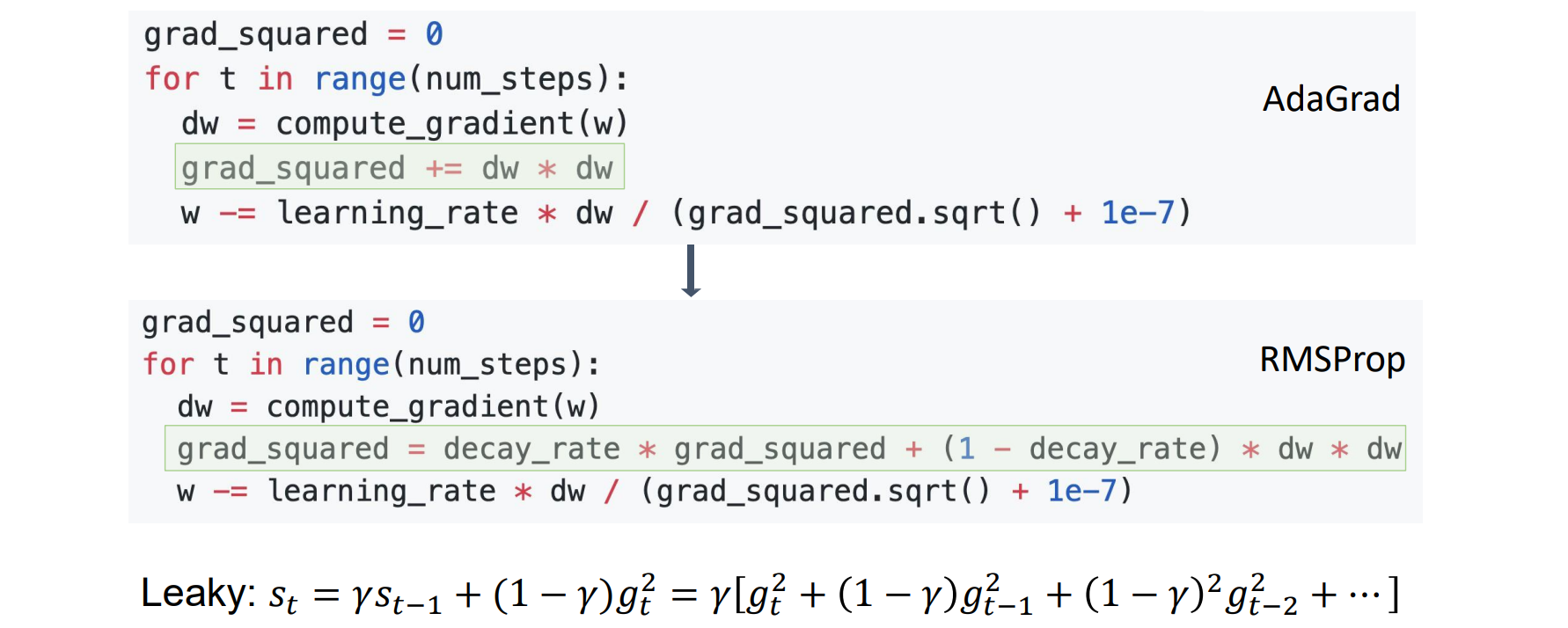
梯度归一化，而不是累加梯度，对grad_squared和dw*dw进行加权平均

Adam: RMSProp + Momentum

Adam (Adaptive Momentum) combines the benefits of RMSProp and Momentum
误差校正：用1/(1-β**t)进行校正

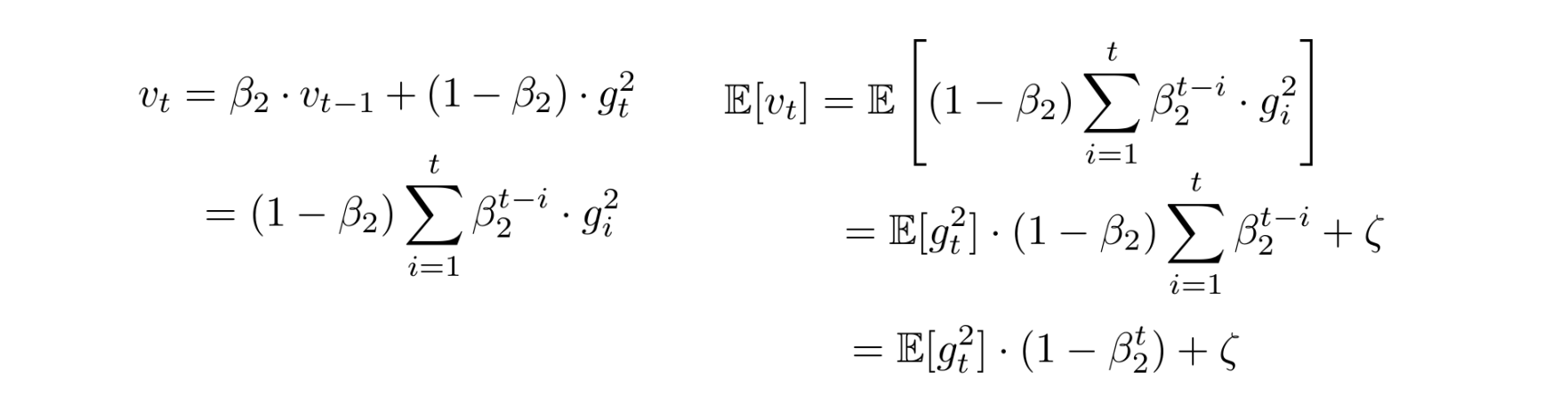
moment1 = 0
moment2 = 0
for t in range(1, num_steps + 1):
    dw = compute_gradient(w)
    # 累积一阶矩、二阶矩
    moment1 = beta1 * moment1 + (1 - beta1) * dw
    moment2 = beta2 * moment2 + (1 - beta2) * dw * dw
    moment1_unbias = moment1 / (1 - beta1 ** t)
    moment2_unbias = moment2 / (1 - beta2 ** t)
    w -= lr * moment1_unbias / (moment2_unbias.sqrt() + 1e-7)

L2 Regularization vs Weight Decay:Due to the gradient normalization in Adam, Weight Decay is “canceled”，因此应该显式的加入weight decay