计算机视觉 20 RNN and Transformers

RNN

Recurrent Neural Networks: Process Sequences

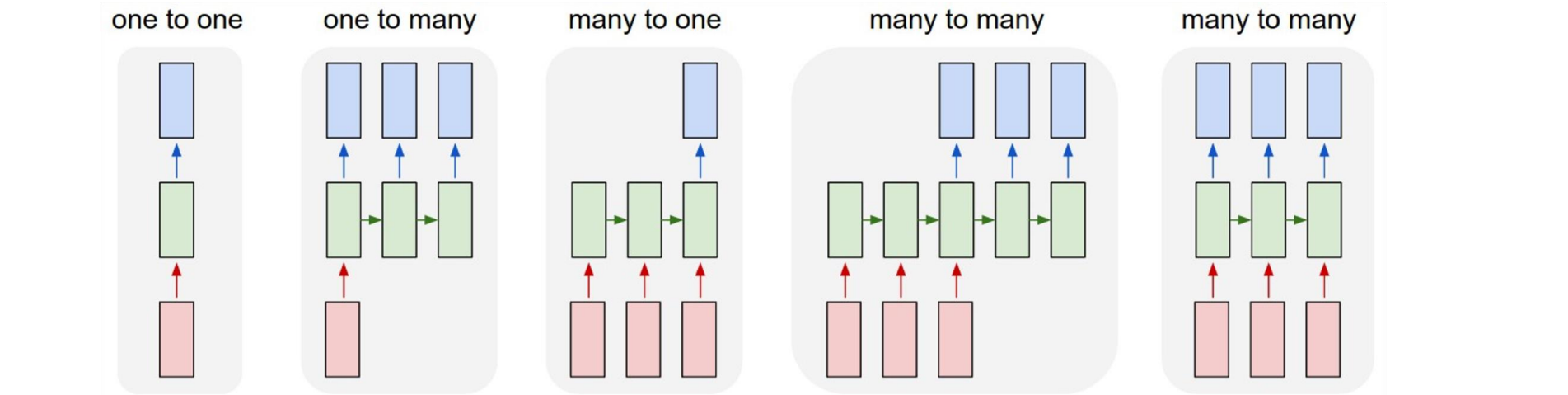
• 一对多：看图说话，输入一张图片输出一个文字序列，无法用CNN解决

• 多对一：视频分类，输入一个序列的图片，输出一个标签，无法用CNN解决

• 异步多对多：翻译，输入一个文字的序列，异步输出一个文字序列，无法用CNN解决

• 同步多对多：每帧视频分类，输入一个图片序列，输出一个标签序列，无法用CNN解决

• RNN用于处理序列问题

Sequential Processing of Non-Sequential Data

• 对于非序列的数据，可以将其进行序列化转化为序列数据进行RNN

Recurrent Neural Networks

• 实现思想：维护一个内部状态，随输入输出不断更新

• 可以通过在每个时间步应用想通的递归公式来处理向量序列x，得到对应位置的y

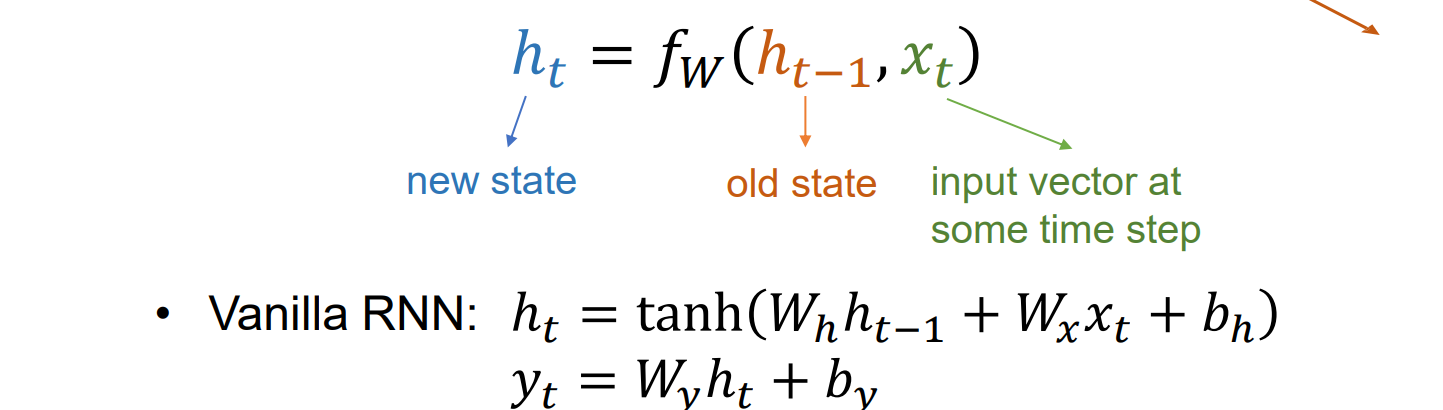
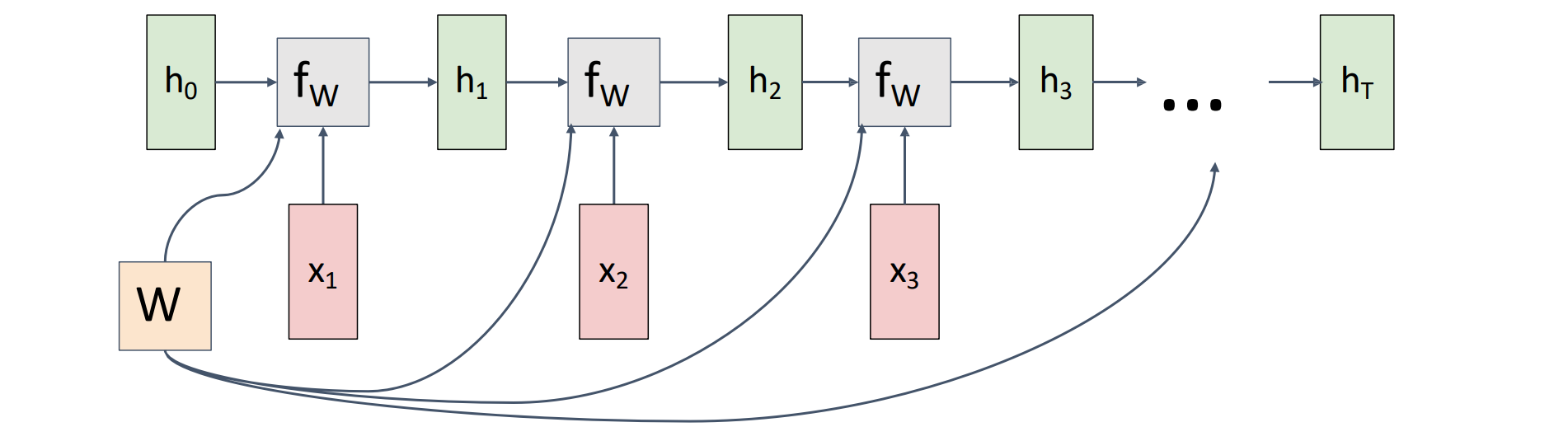
RNN Computational Graph

• 初始化隐藏层为0或者随机数来进行学习

• 在每个时间步长重复使用相同的权重矩阵

• 而many to many问题的计算图可以表示成：

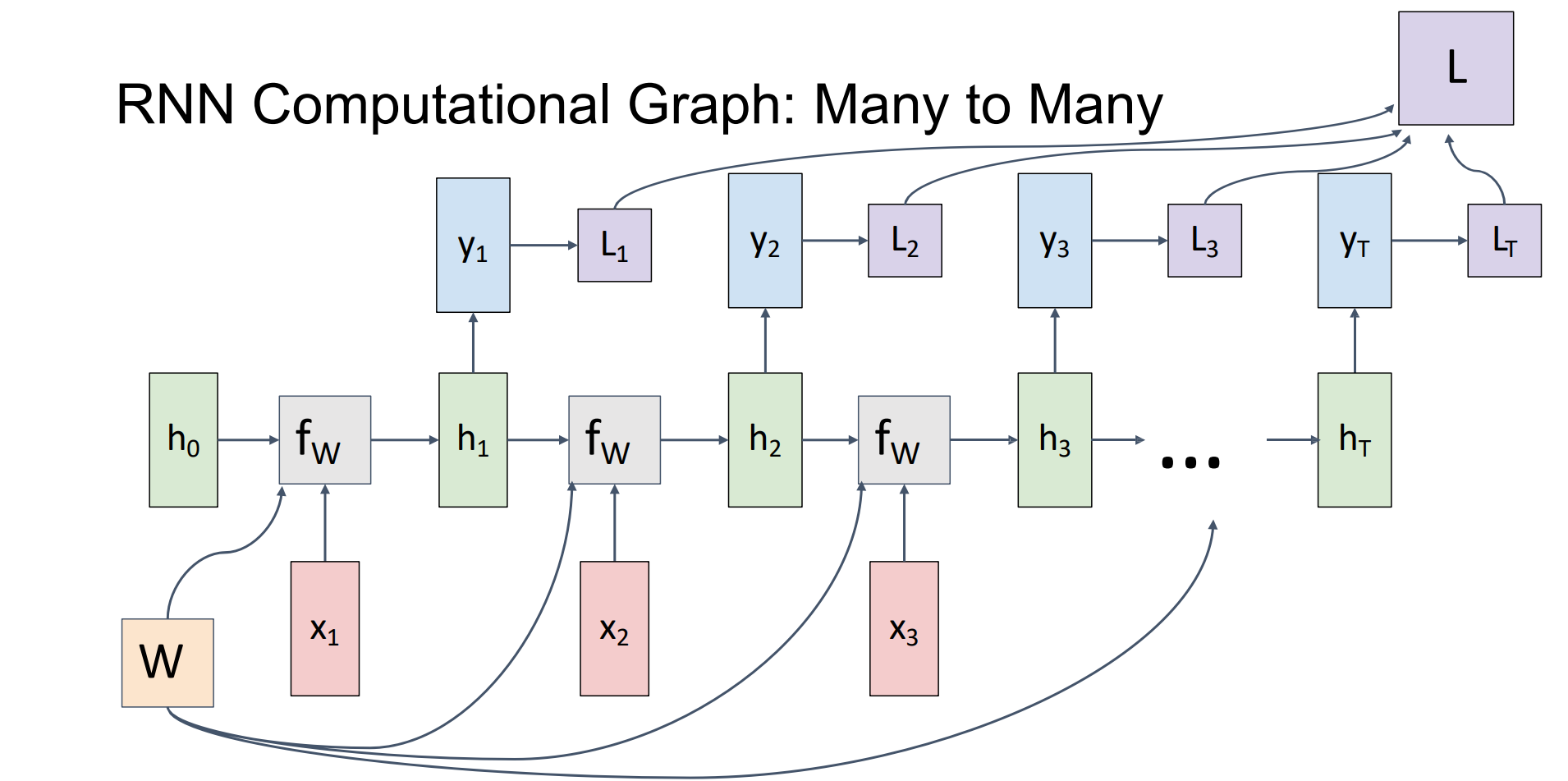
• 其中总损失函数是累加而得，因为权重矩阵是相同的(复制)，因此总梯度是局部梯度累加而得，通过梯度下降法更新

RNN Computational Graph: Sequence to Sequence

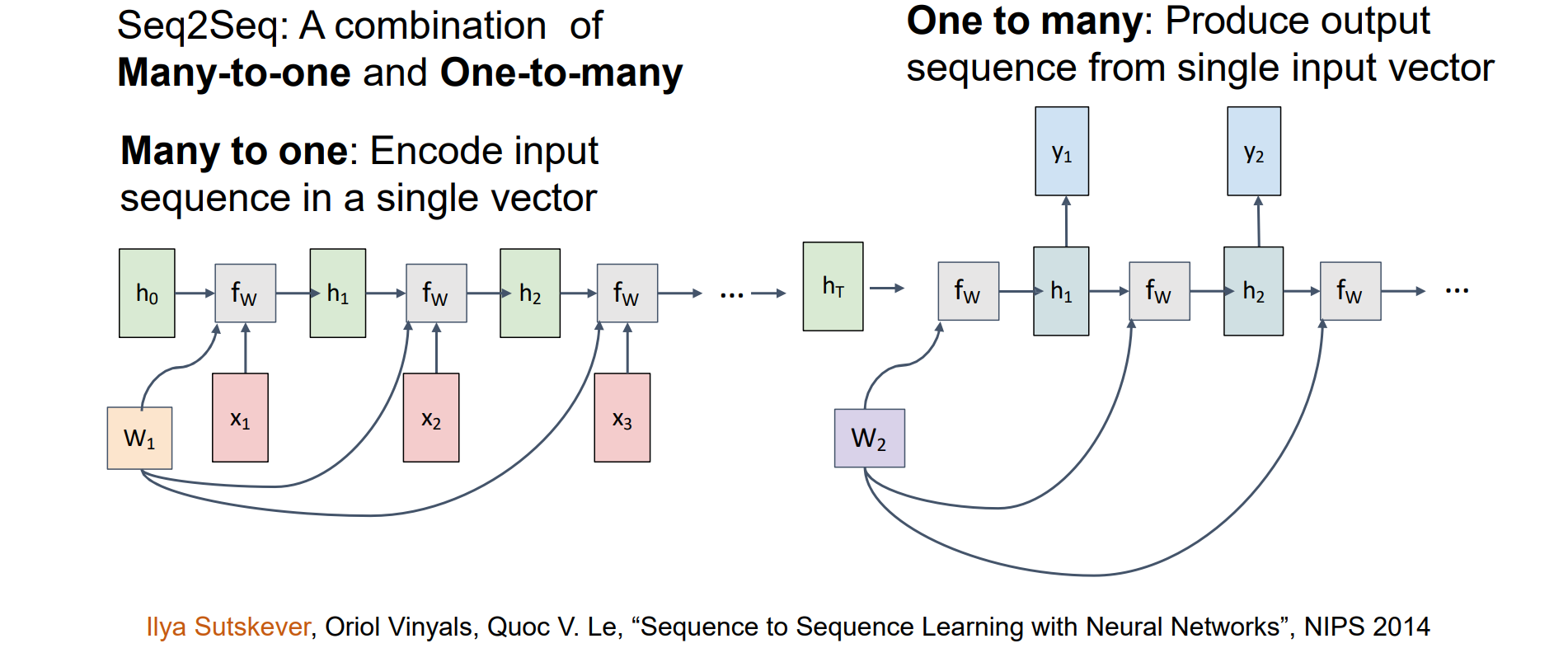
• Seq2Seq:是Many-to-one和One-to-many的组合：

  1. Many to one:在单个向量中编码输入序列
  2. One to many:从单个输入向量生成输出序列

• 相当于先对输入进行理解形成隐状态，再从隐状态中解码获得输出，设置隐状态的原因是异步Seq2Seq任务是需要对整个输入序列进行理解，例如对整个句子进行翻译

Example: Language Modeling

• 目标：给定字符1，2，…，t-1，模型预测字符 t，将1，2，…，t-1吸收为隐状态

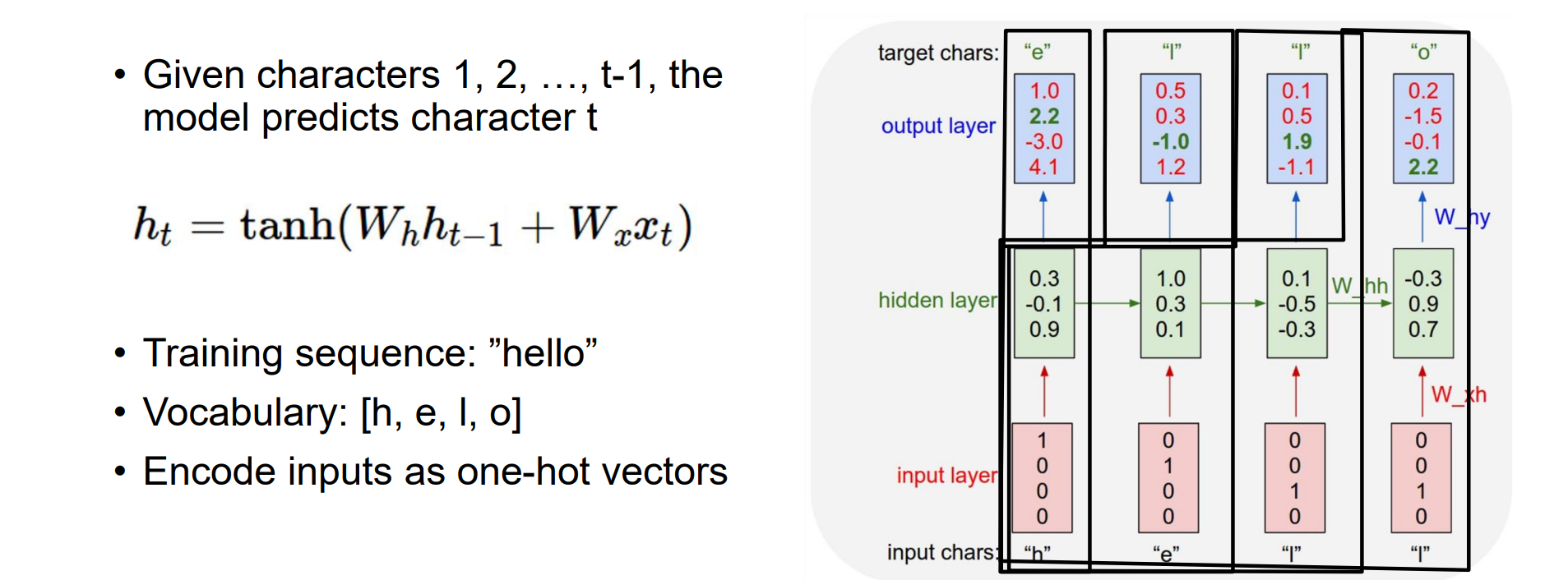
• 在测试时，生成新文本：一次一个示例字符，反馈给模型。先给定h，e作为真实的预测值进行训练，然后将h,e作为输入，l作为真实的预测值进行训练…

• 将每一个字映成one-hot编码形式

• GPT的原理类似

• 训练方式被称为teach forcing：训练时有真实标签，测试时没有真实标签

Backpropagation Through Time

• 向前遍历整个序列以计算loss，然后向后遍历整个序列以计算梯度

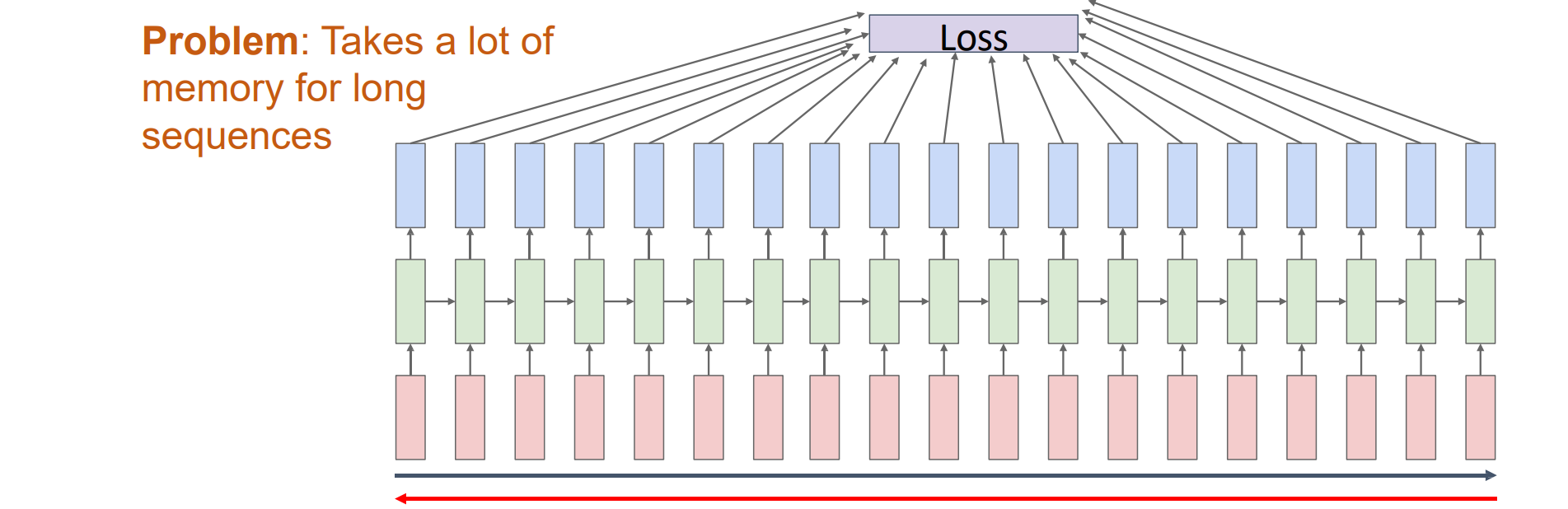
• 当序列比较长的时候w需要经过多次复制，因此梯度传播路径很长，计算所需空间内存较大

Truncated Backpropagation Through Time

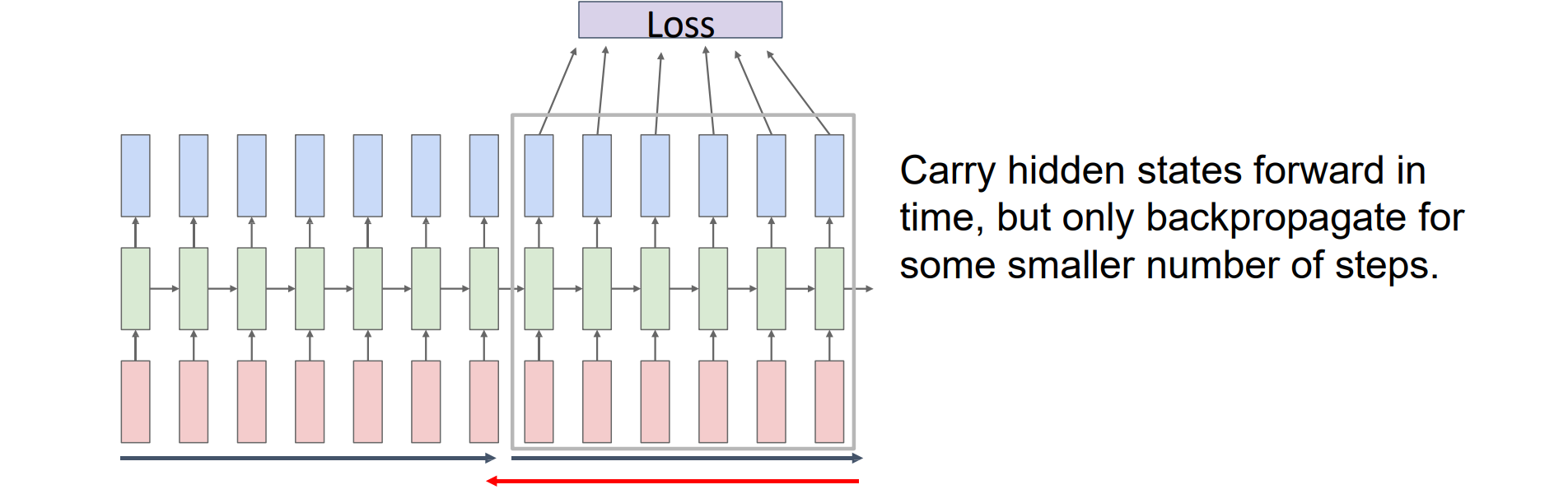
• 向前和向后运行序列的块，而不是整个序列，采样batch计算梯度来进行截断

• 在时间上向前推进隐藏状态，但仅对少量步骤进行反向传播

Example: Image Captioning with RNN

• 字典：常见字符

• 先用CNN进行图像特征提取得到feature，再把feature输入到RNN中进行图像描述任务

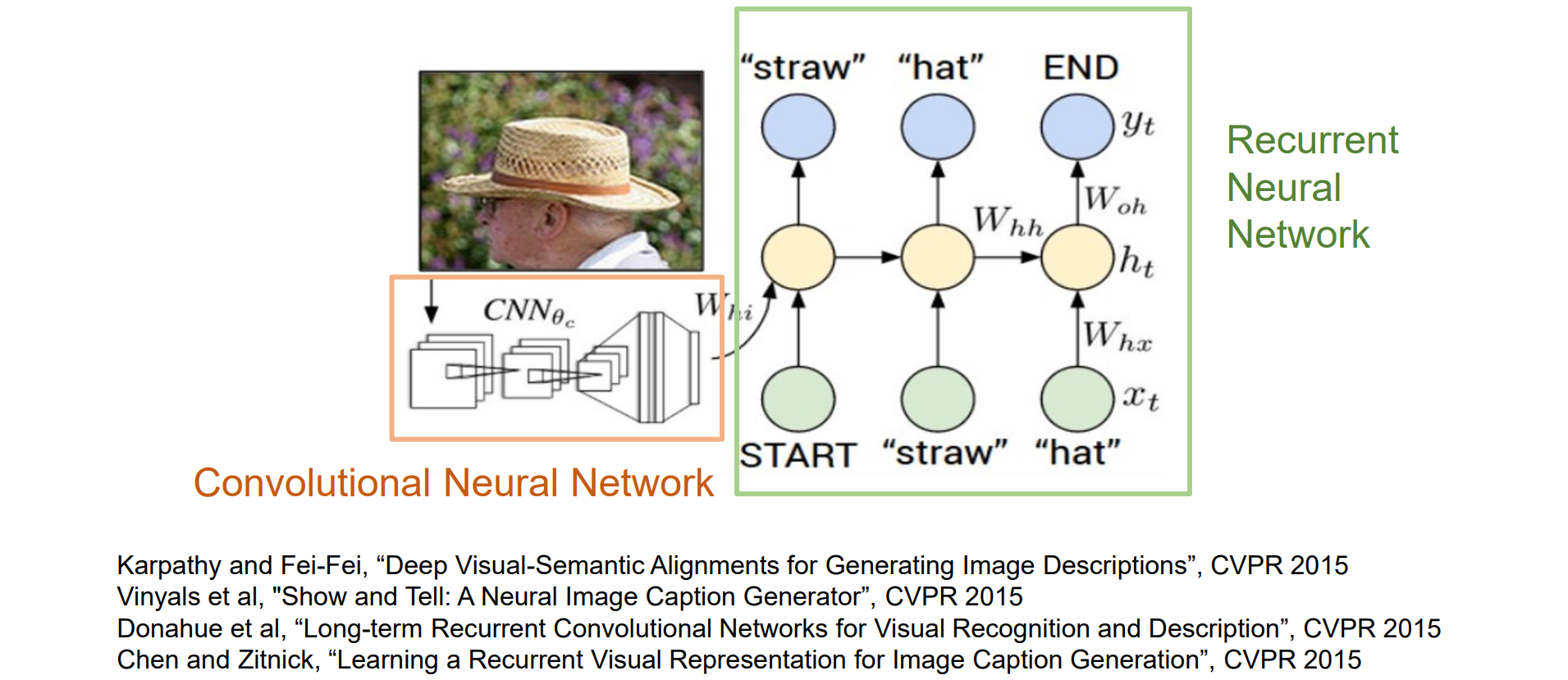
• 如何将feature加入到RNN中：

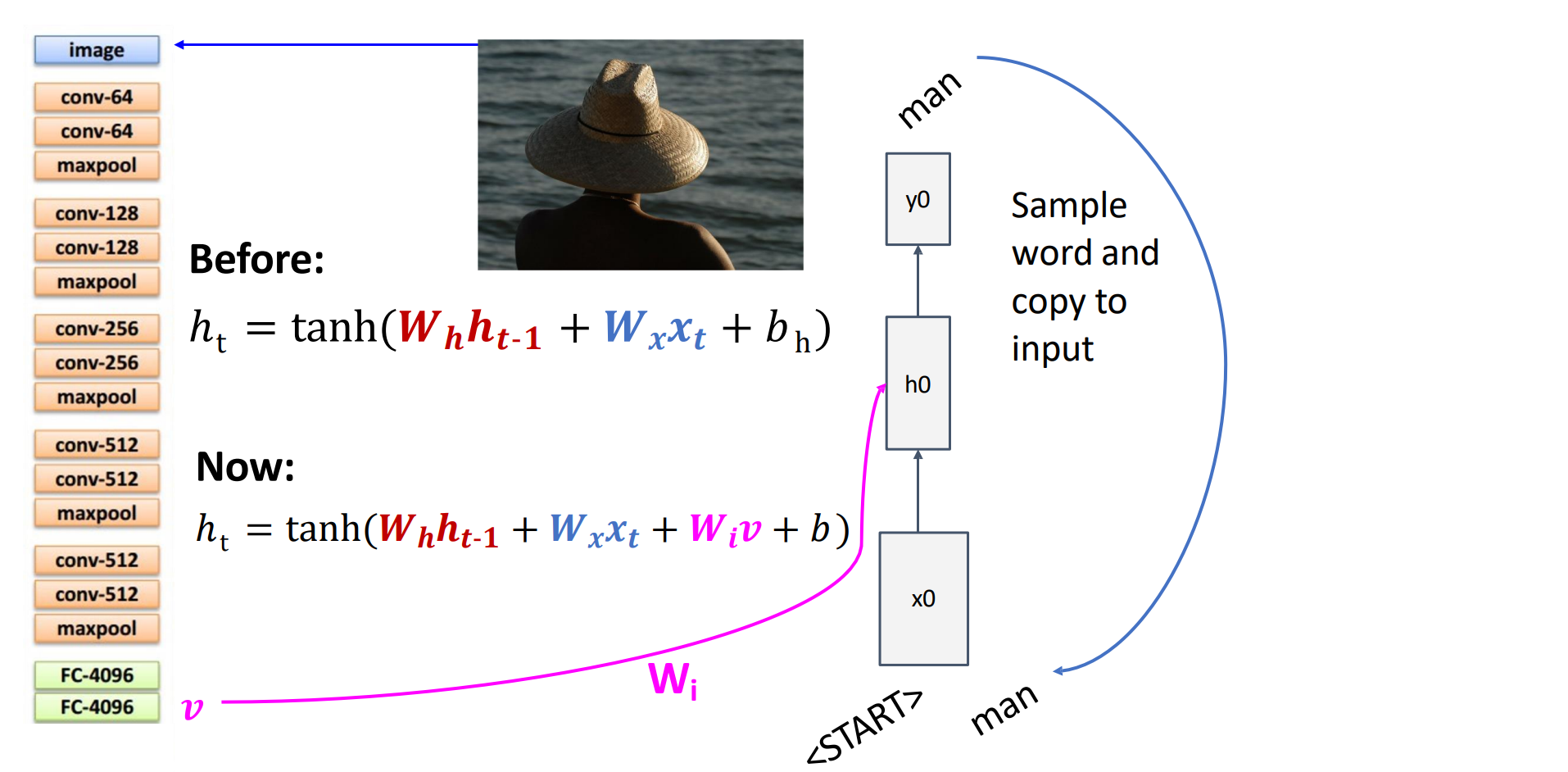
• 注意训练是异步的

Vanilla RNN Gradient Flow

• 以下红线代表梯度反向传播中梯度的流动方向

• 问题：训练不稳定，出现梯度消失和爆炸的问题

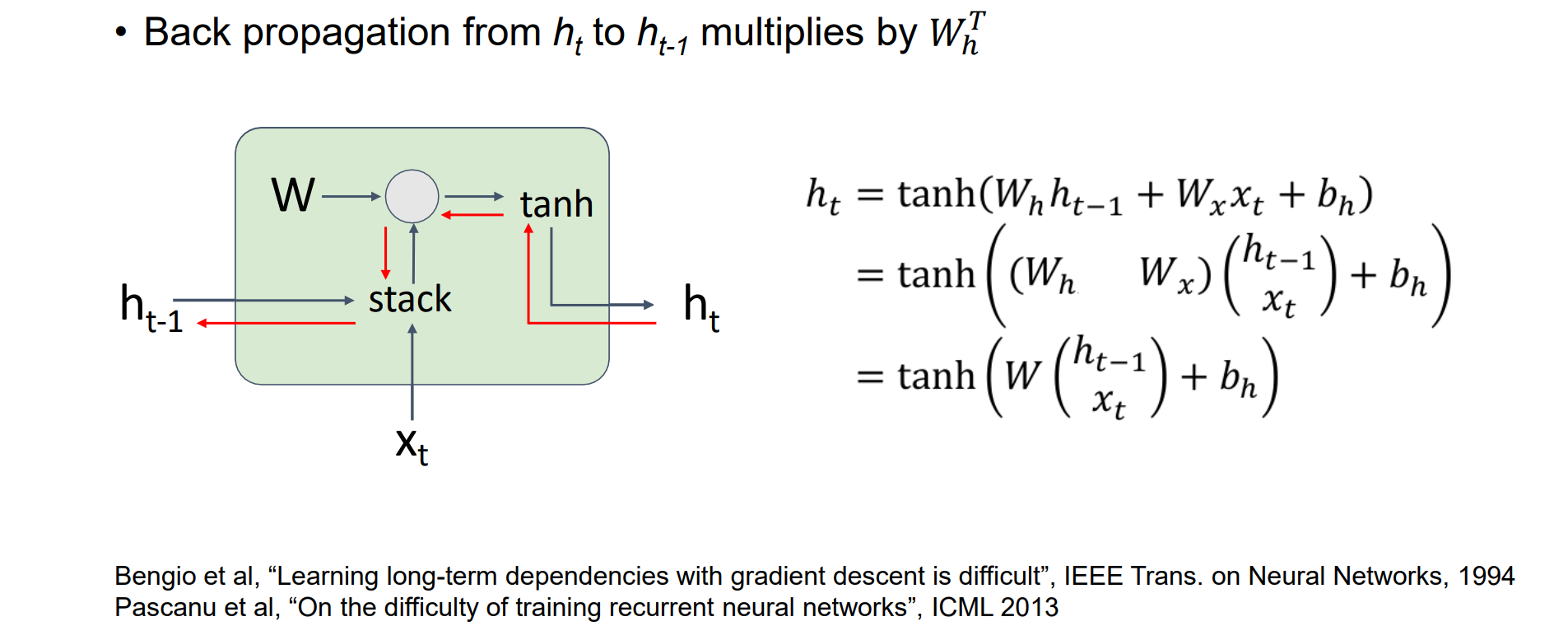
• 公式化简说明：RNN可以视为被循环使用的线性层

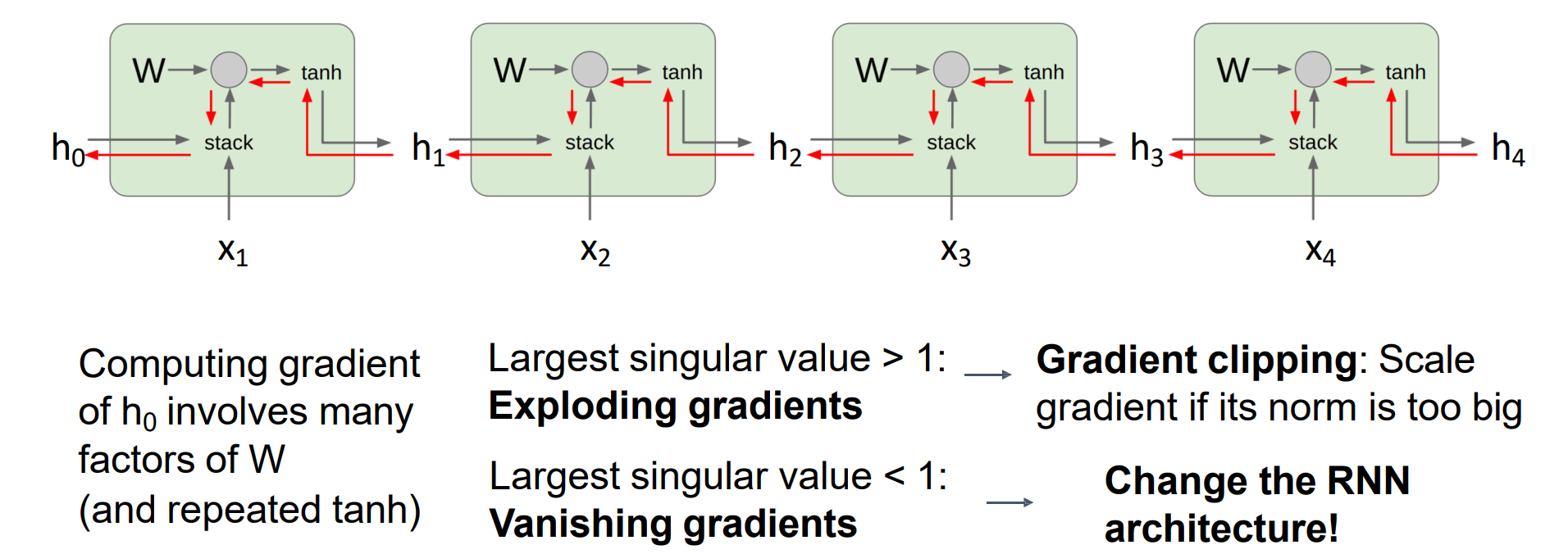
• 梯度传播过程中一系列的w相乘：

  1. 若奇异值>0，则会出现放大作用，可能导致梯度爆炸
  2. 若奇异值<0，则会出现减小作用，可能导致梯度消失

• 解决方法：加入LSTM，可以类比于ResNet

• Vanilla RNN：

import torch
import torch.nn as nn
import torch.nn.functional as F

class VanillaRNN(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(VanillaRNN, self).__init__()
        
        # 定义输入到隐藏层的权重矩阵 W_ih 和隐藏层到隐藏层的权重矩阵 W_hh
        self.W_ih = nn.Parameter(torch.randn(hidden_size, input_size))
        self.W_hh = nn.Parameter(torch.randn(hidden_size, hidden_size))
        self.b_h = nn.Parameter(torch.zeros(hidden_size))
        
        # 定义隐藏层到输出层的权重矩阵 W_ho
        self.W_ho = nn.Parameter(torch.randn(output_size, hidden_size))
        self.b_o = nn.Parameter(torch.zeros(output_size))

    def forward(self, x):
        # 初始化隐藏状态 h
        h = torch.zeros(self.W_hh.size(0), device=x.device)
        
        # 遍历输入序列的每个时间步
        for t in range(x.size(0)):
            # 计算当前时间步的隐藏状态 h_t
            h = torch.tanh(torch.matmul(self.W_ih, x[t]) + torch.matmul(self.W_hh, h) + self.b_h)
        
        # 计算输出
        output = torch.matmul(self.W_ho, h) + self.b_o
        return output

Long Short Term Memory (LSTM)

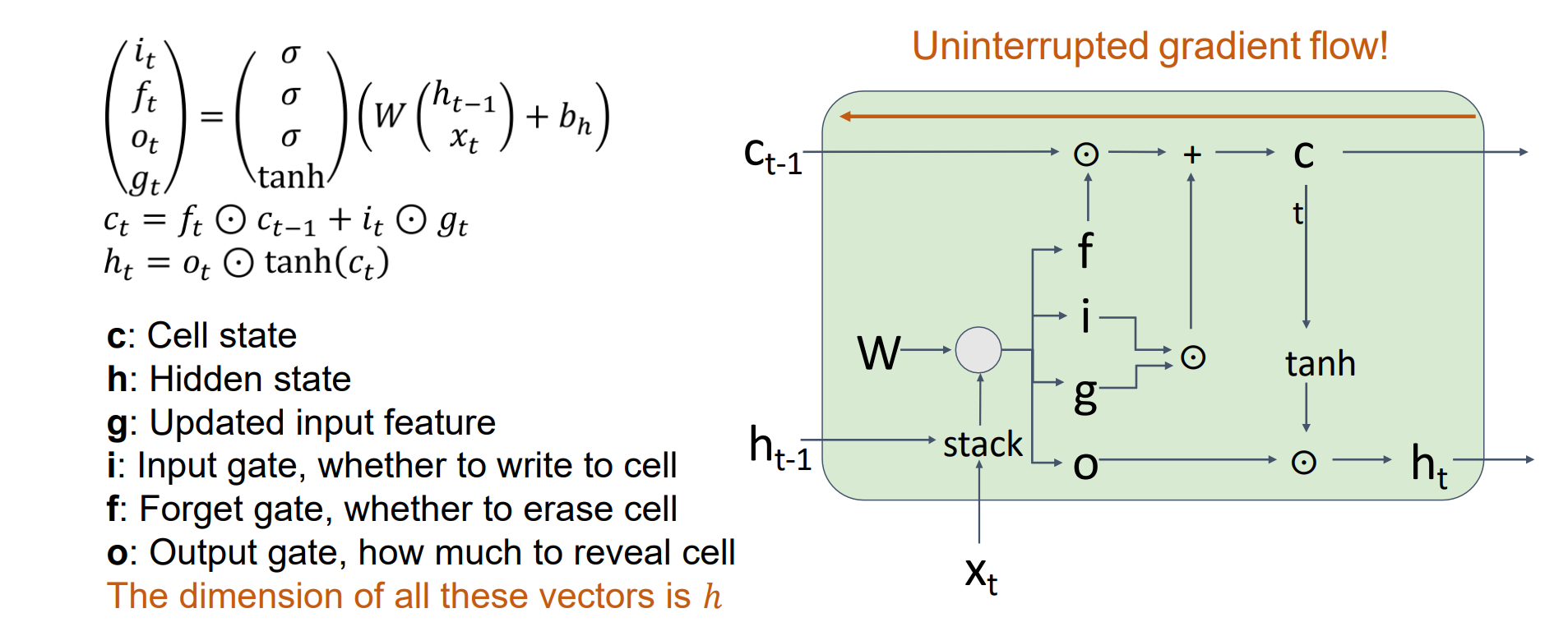
• 和RNN相比多了cell层和门，梯度可以再流畅传播，解决了梯度消失爆炸的问题

• i是输入门，决定有多少状态更新cell

• f是遗忘门，决定有多少概率忘记

• g是更新后的feature

• 历史(Ct-1)一部分忘记(ft)，一部分输入(it)更新cell state，cell state和ot来更新隐层藏ht

• LSTM_RNN:

import torch
import torch.nn as nn

class LSTM_RNN(nn.Module):
    def __init__(self, input_size, hidden_size, output_size, num_layers=1, dropout=0.5):
        super(LSTM_RNN, self).__init__()
        
        # 定义 LSTM 层
        self.lstm = nn.LSTM(input_size=input_size, 
                            hidden_size=hidden_size, 
                            num_layers=num_layers, 
                            batch_first=True, 
                            dropout=dropout)
        
        # 定义全连接层
        self.fc = nn.Linear(hidden_size, output_size)
    
    def forward(self, x):
        # x 的形状应为 (batch_size, seq_len, input_size)
        lstm_out, (h_n, c_n) = self.lstm(x)
        
        # 取最后一个时间步的隐藏状态作为特征
        last_hidden_state = h_n[-1]
        
        # 通过全连接层得到输出
        output = self.fc(last_hidden_state)
        return output

Multi-Layer RNNs

• 将隐藏状态从一个 RNN 作为输入传递到另一个 RNN，形成多层RNN

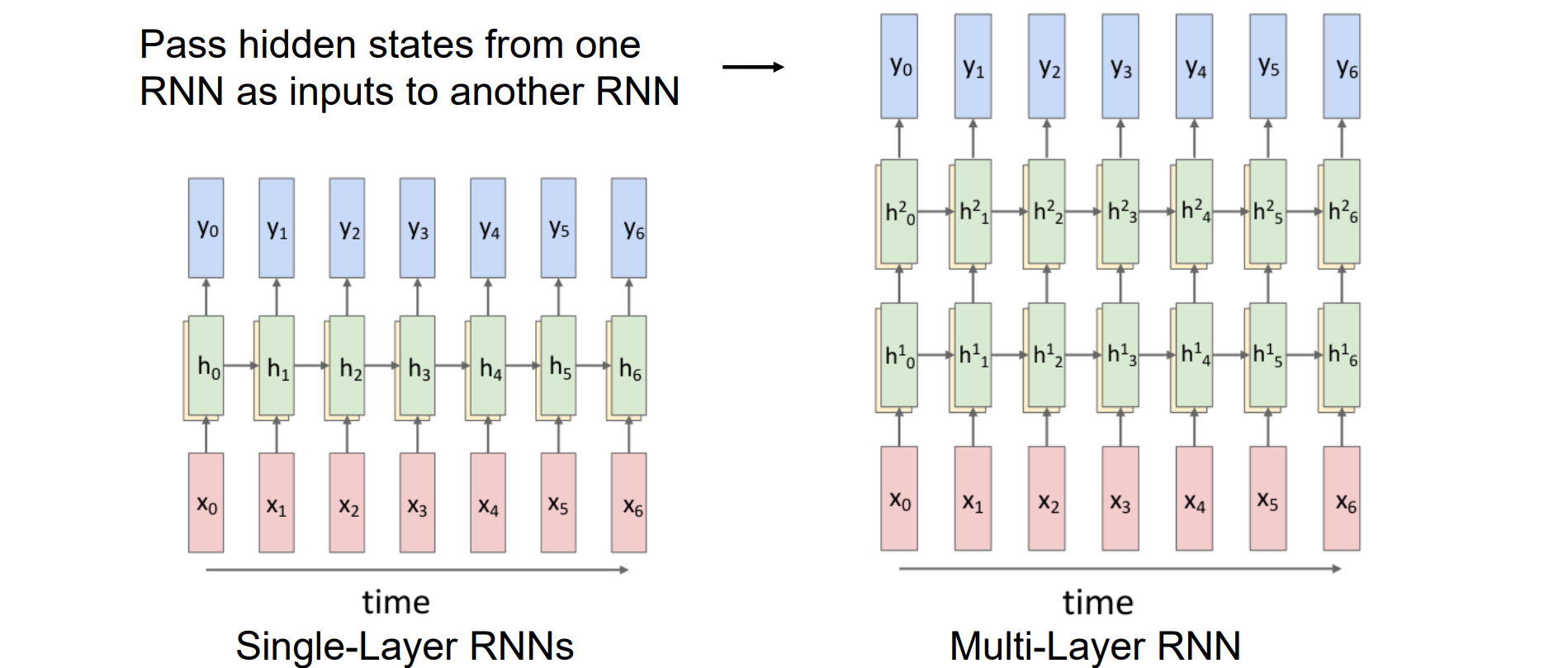
• 其中每一列都可以视为一个CNN

Transformer

Motivation of Attention

• RNN的优点：计算高效

• RNN的缺点：使用 RNN 的Seq2Seq模型的问题：输入序列通过固定大小的向量出现bottlenet问题，压缩成隐藏层时信息有损失，希望能够输出与输入直接有关联

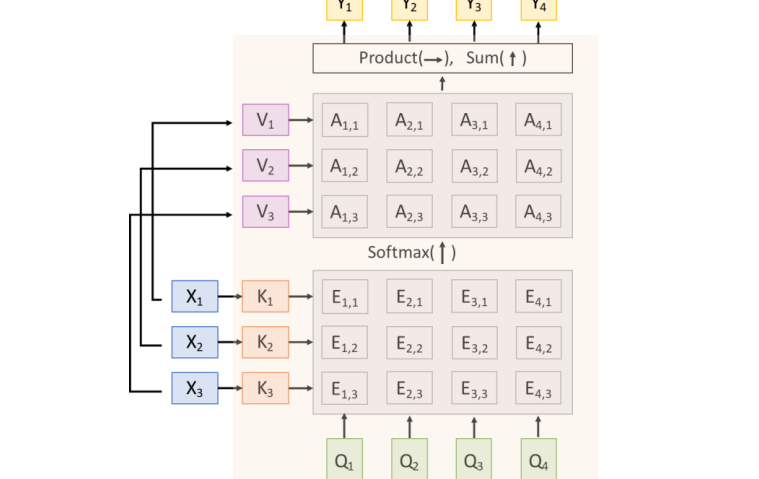
Attention Layer

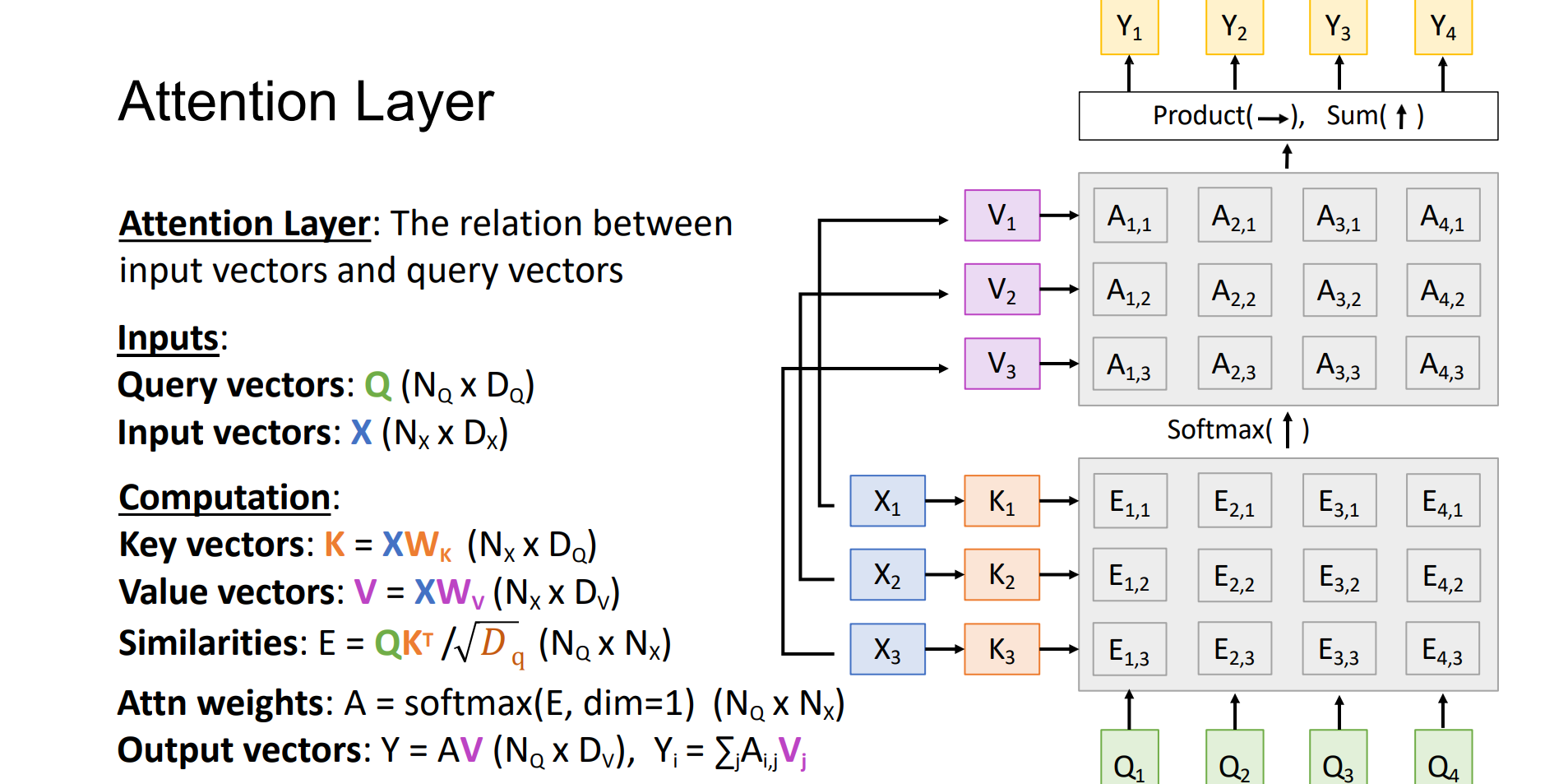
• Attention Layer:input vectors和query vectors找相互关系，类似于可微分的检索

• 输入：

  1. Query vectors: Q (NQ x DQ)，有NQ个q,维度是DQ
  2. Input vectors: X (NX x DX)，有NX个x,维度是DX

• key和value均为XW计算得到

• 用Q在X中找最近邻，和什么key最相似

• Similarities: E = QK.T / sqrt(𝐷q)x(NQ x NX)

• Attn weights: A = softmax(E, dim=1) (NQ x NX)，得到的是概率矩阵，每一列相加为1

• Output vectors: Y = AV (NQ x DV), Yi = ∑jA(i,j)Vj

• Self Attention: compute 𝑄 from 𝑋, 𝑄 = 𝑋𝑊𝑞，Q与X相关。否则称为Cross Attention

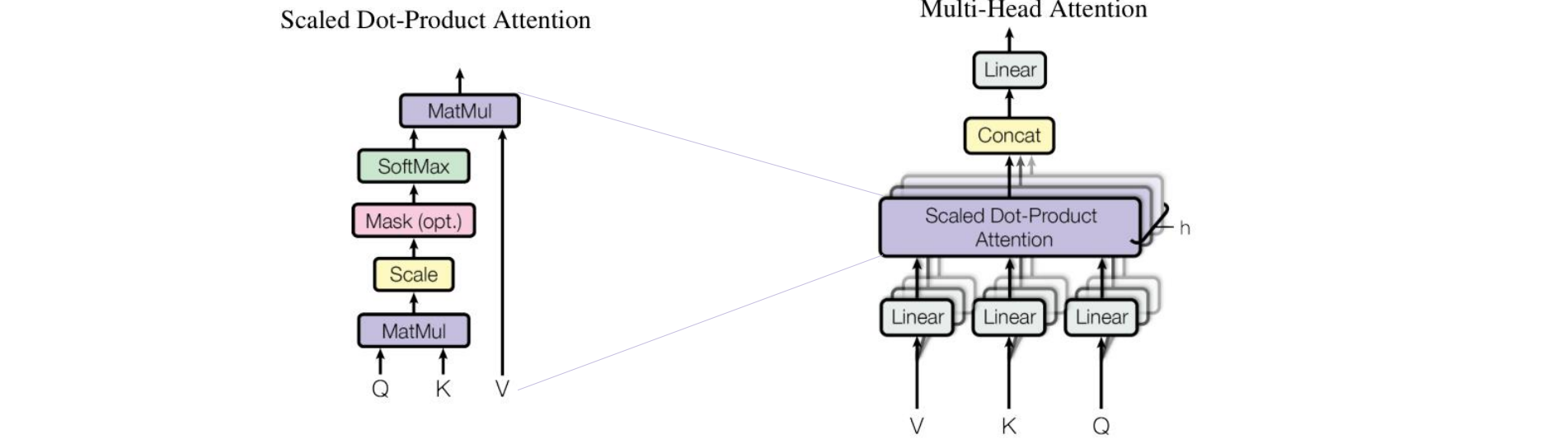
• Scaled Dot-Product Attention: 𝐴𝑡𝑡𝑒𝑛𝑡𝑖𝑜𝑛(𝑄,𝐾,𝑉) = 𝑠𝑜𝑓𝑡𝑚𝑎x(E)，使用sqrt(dk)：当 DK 较大时，点积的幅度会增大，从而将 SoftMax 函数推入梯度极小的饱和区。÷sqrt(dk)后方差为1

• Attention is permutation equivariant(交换不变性)：考虑排列 input 向量，那么 Queries、Keys、Values 和 Outputs 将相同，但也进行了置换

• 因此需要显式的将位置信息加入到神经网络中：将位置编码 PE 连接或添加到输入，PE 可以是学习的查找表，也可以是位置的 sin/cos 特征

Multi-Head Attention

• 问题：Q点乘K只有一种可能得结果，相互关系太简单，因此要进行分组

• 实现思路：

  1. 线性投影查询、键和值 h 次
  2. 并行执行 h 次的 attention 函数，然后拼接并投影结果

Transformer Block

• Transformer Block由多个self-attention层和多个MLP层拼接而成

• 实现思路：

  1. 先对x进行正则化，应该对c个通道正则化，沿着D维度进行正则化
  2. 然后用attention计算元素相互关系
  3. 加入残差连接
  4. 进行正则化
  5. MLP进行通道间的变换
  6. 加入残差连接

• 可以高度并行化，规模化实现

• LayerNorm 和 MLP向量独立工作，Self-attention是向量之间唯一的交互

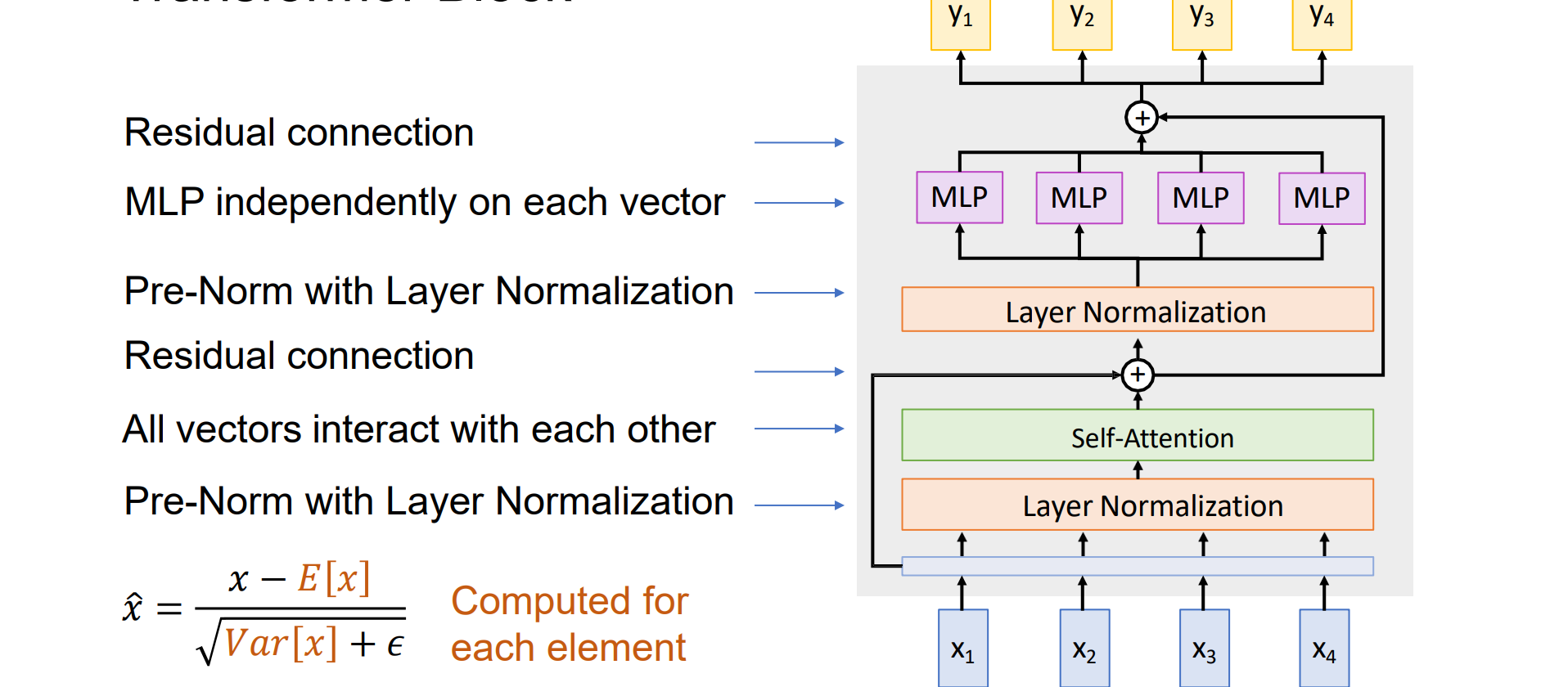
• Transformer Block:

import torch
import torch.nn as nn
import torch.nn.functional as F
import math

class MultiHeadAttention(nn.Module):
    def __init__(self, embed_dim, num_heads):
        super(MultiHeadAttention, self).__init__()
        self.num_heads = num_heads
        self.embed_dim = embed_dim
        self.head_dim = embed_dim // num_heads

        assert self.head_dim * num_heads == embed_dim, "Embedding dimension must be divisible by number of heads"

        self.query = nn.Linear(embed_dim, embed_dim)
        self.key = nn.Linear(embed_dim, embed_dim)
        self.value = nn.Linear(embed_dim, embed_dim)
        self.fc_out = nn.Linear(embed_dim, embed_dim)

    def forward(self, values, keys, query, mask):
        N = query.shape[0]
        value_len, key_len, query_len = values.shape[1], keys.shape[1], query.shape[1]

        # Split the embedding into self.num_heads different pieces
        values = values.reshape(N, value_len, self.num_heads, self.head_dim)
        keys = keys.reshape(N, key_len, self.num_heads, self.head_dim)
        query = query.reshape(N, query_len, self.num_heads, self.head_dim)

        values = values.permute(2, 0, 1, 3)
        keys = keys.permute(2, 0, 1, 3)
        query = query.permute(2, 0, 1, 3)

        energy = torch.einsum("qnhd,knhd->qnhk", [query, keys])

        if mask is not None:
            energy = energy.masked_fill(mask == 0, float("-1e20"))

        attention = torch.softmax(energy / (self.head_dim ** (1 / 2)), dim=-1)

        out = torch.einsum("qnhk,vnhd->qnhd", [attention, values]).reshape(
            self.num_heads, N, query_len, self.head_dim
        )

        out = out.permute(1, 2, 0, 3).reshape(N, query_len, self.num_heads * self.head_dim)

        out = self.fc_out(out)

        return out

class TransformerBlock(nn.Module):
    def __init__(self, embed_dim, num_heads, expansion_factor=4, dropout=0.1):
        super(TransformerBlock, self).__init__()

        self.attention = MultiHeadAttention(embed_dim, num_heads)
        self.norm1 = nn.LayerNorm(embed_dim)
        self.norm2 = nn.LayerNorm(embed_dim)
        self.feed_forward = nn.Sequential(
            nn.Linear(embed_dim, expansion_factor * embed_dim),
            nn.ReLU(),
            nn.Linear(expansion_factor * embed_dim, embed_dim)
        )
        self.dropout1 = nn.Dropout(dropout)
        self.dropout2 = nn.Dropout(dropout)

    def forward(self, value, key, query, mask):
        attention = self.attention(value, key, query, mask)
        attention = self.dropout1(attention)
        x = self.norm1(attention + query)
        forward = self.feed_forward(x)
        forward = self.dropout2(forward)
        out = self.norm2(forward + x)
        return out

Transformer

• Transformer由多个transformer block形成

• Vaswani et al: 12 blocks, DQ=512, 6 heads

• Transformer:

import torch
import torch.nn as nn

# 定义模型参数
d_model = 512  # 模型维度
nhead = 6      # 注意力头数
num_layers = 12  # Transformer块的层数

# 初始化Transformer模型
transformer = nn.Transformer(
    d_model=d_model,
    nhead=nhead,
    num_encoder_layers=num_layers,
    num_decoder_layers=num_layers,
    dim_feedforward=2048,  # 前馈神经网络的维度
    dropout=0.1,          # Dropout概率
    activation='relu',    # 激活函数
    batch_first=True      # 输入和输出的形状为(batch, seq, feature)
)

# 创建示例输入数据
# 假设输入序列长度为10，批次大小为32
src = torch.rand((32, 10, d_model))  # 源序列
tgt = torch.rand((32, 10, d_model))  # 目标序列

# 前向传播
output = transformer(src, tgt)

Three Ways of Processing Sequences

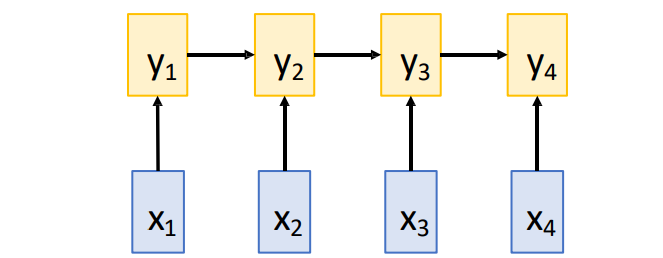
RNN

• 优点：省内存

• 长序列：在一个 RNN 层之后“看到”整个序列

• 缺点：难以并行

1D Convolution

• 优点：容易并行

• 缺点：长序列的感受野小

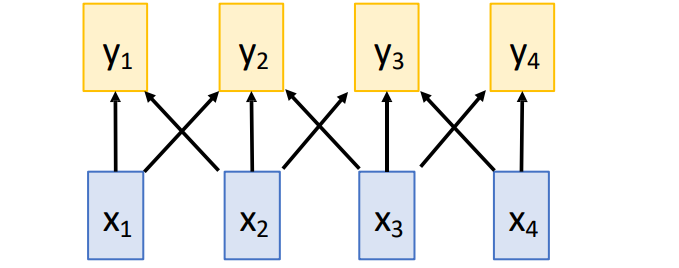
Self-Attention Layer

• 优点：每一个输出可以看到每一个输入，容易并行化规模化

• 缺点：耗内存

Transformers on Pixels

• 将图像转换为序列：从左到右从上到下扫描形成序列

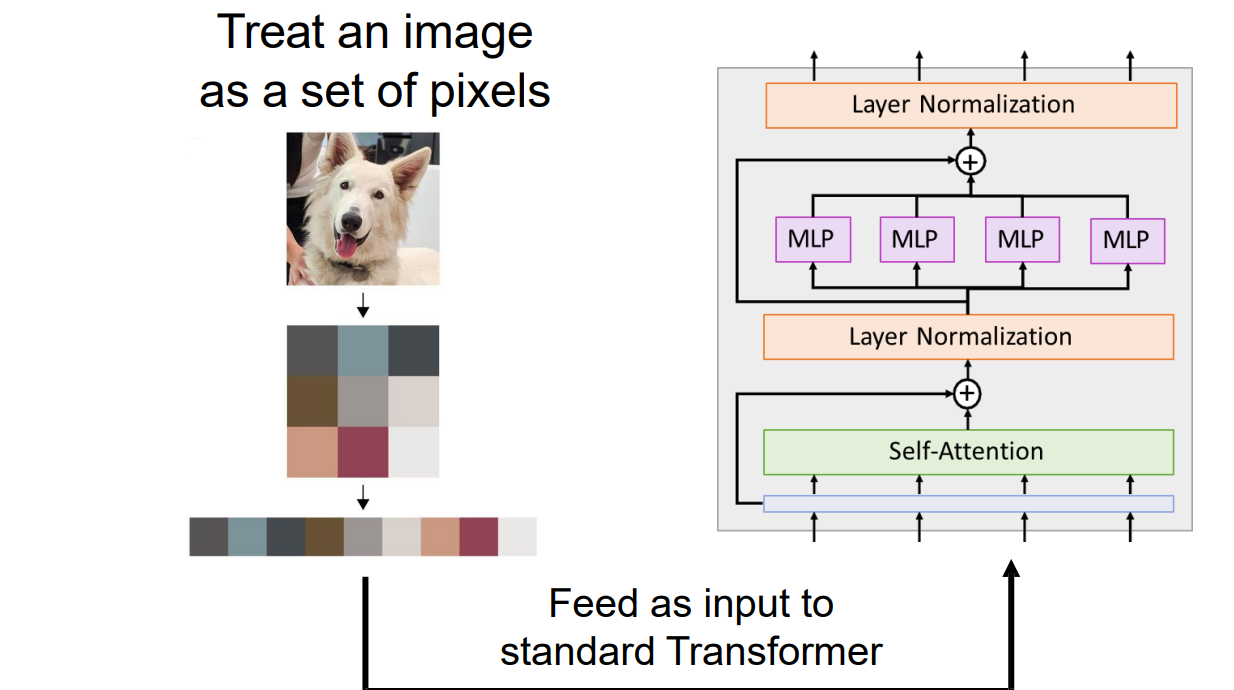
• 问题：高像素会导致计算存储都很大。R x R 图像每个attention矩阵需要 R4 个元素;对于 R=128、48 层、16 个头，单个示例的attention矩阵需要 768GB 的内存

Transformers on Image Patches

• 解决方法：将一个image分成patch形式形成多个token

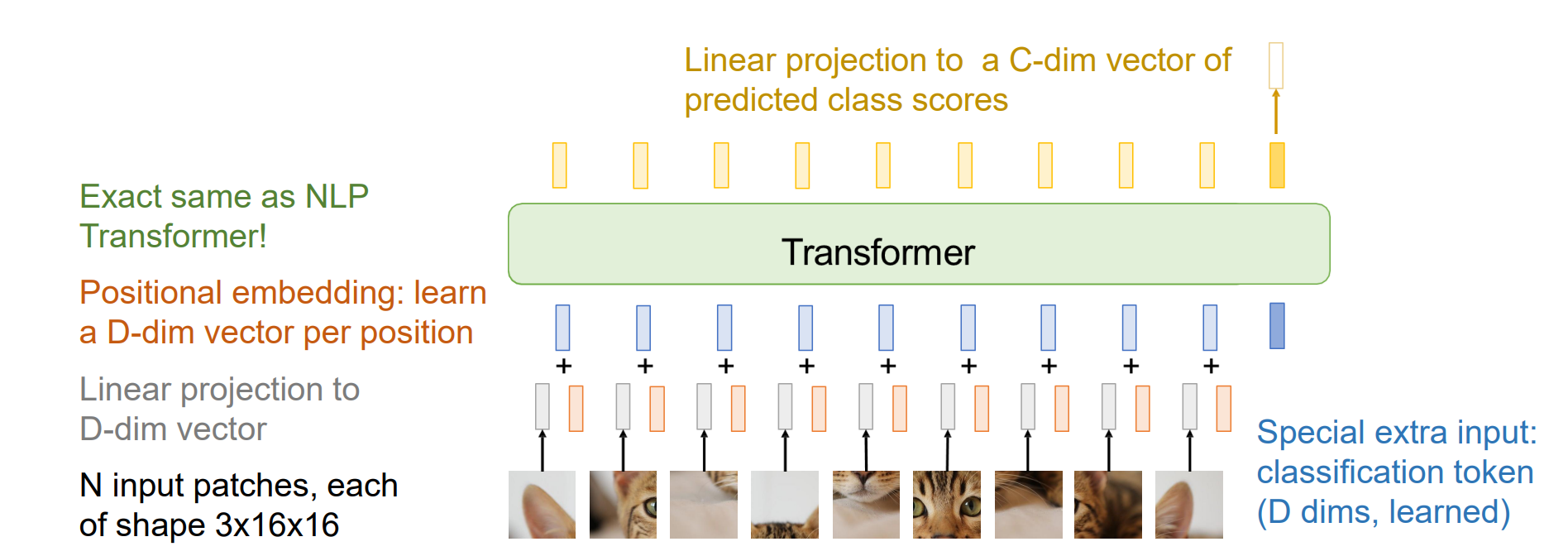
Vision Transformer (ViT)

• 第一个没有卷积的计算机视觉模型

• ViT 在像素上比Transformer效率高得多,在大的数据集上优于ResNet

• 在大多数 CNN（包括 ResNets）中，随着我们在网络中深入，会降低分辨率并增加通道（分层架构Hierarchical architecture）,希望在ViT中也使用Hierarchical architecture，从而更符合视觉

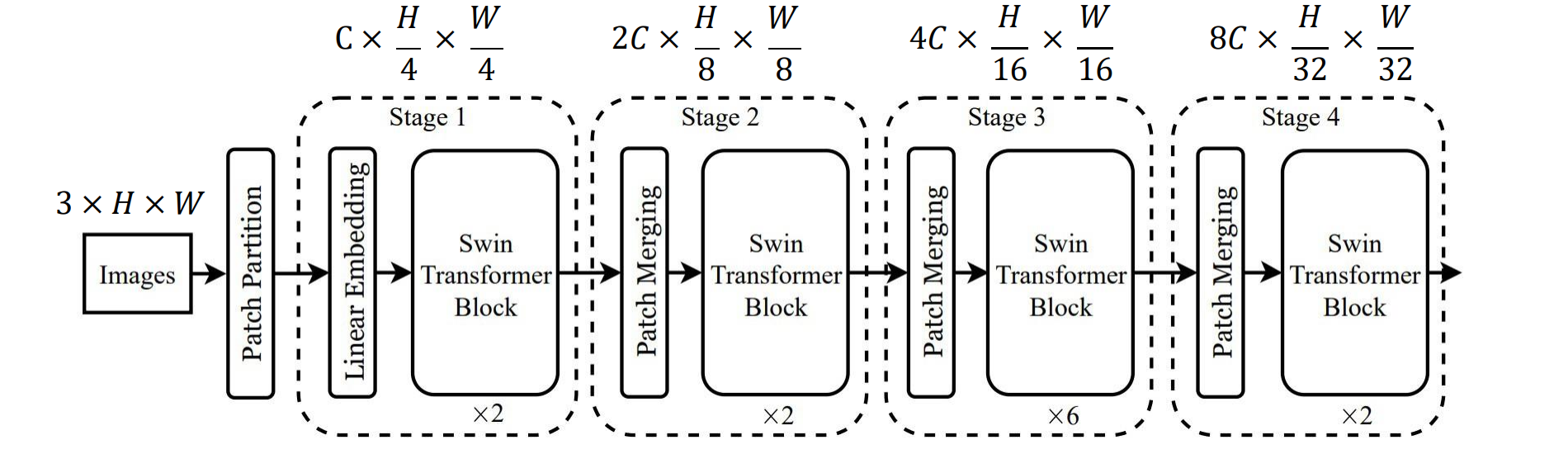
Hierarchical ViT: Swin Transformer

• 进行若干次attention后进行一次降采样：2x2的图像块映射到更高维

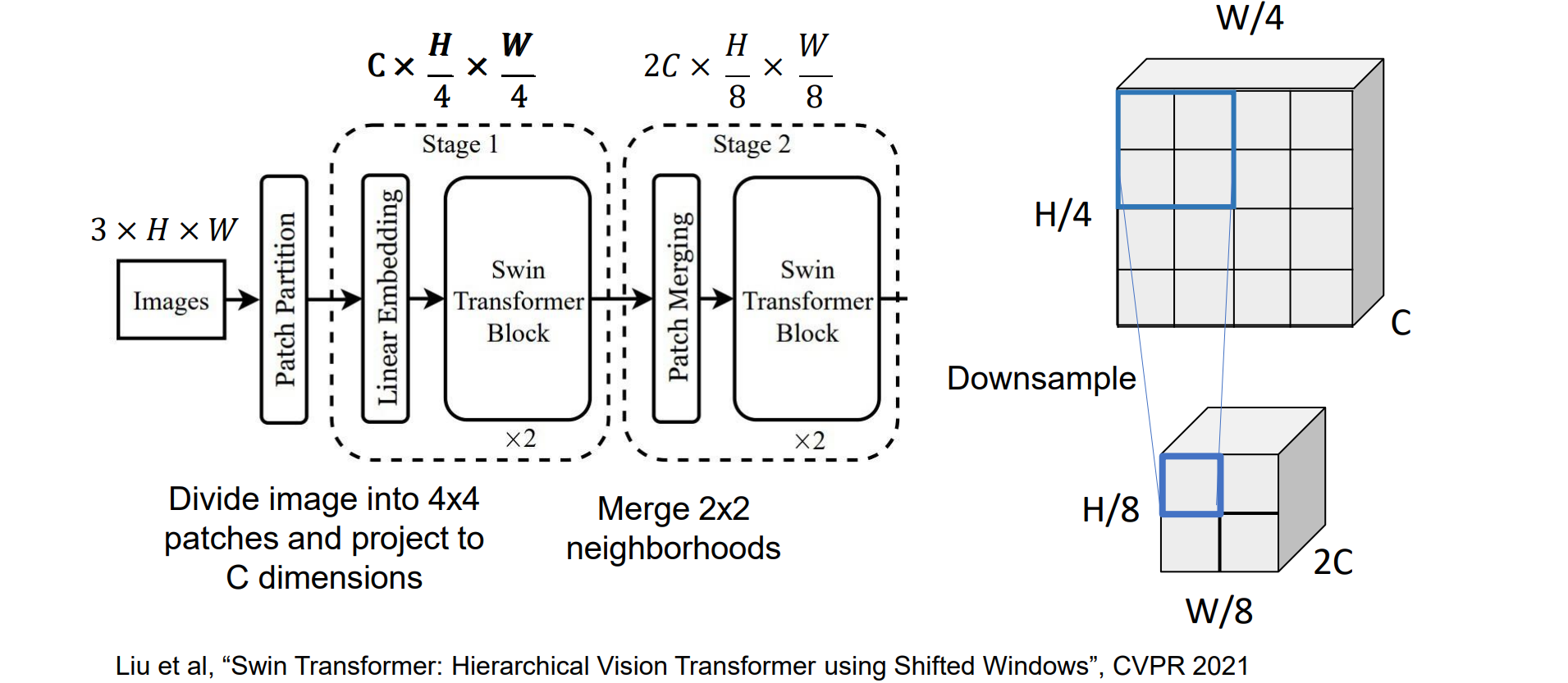
• 问题：元素多，计算量大

• 解决方法：进行图像分块(patch)，在每一块上进行attention

Swin Transformer: Window Attention

• 使用 H x W 标记网格，每个注意力矩阵都是(H^2)(W^2)，即图像大小的二次方

• 不让每个 Token 关注所有其他 Token，而是将图像划分为 M x M Tokens 的窗口（此处为 M=4）;仅计算每个时段内的注意力

• 所有注意力矩阵的总大小现在为：(M^4)（H/M）（W/M） = (M^2)HW

• 问题：Tokens仅与同一窗口内的其他Tokens交互;没有跨Windows交互

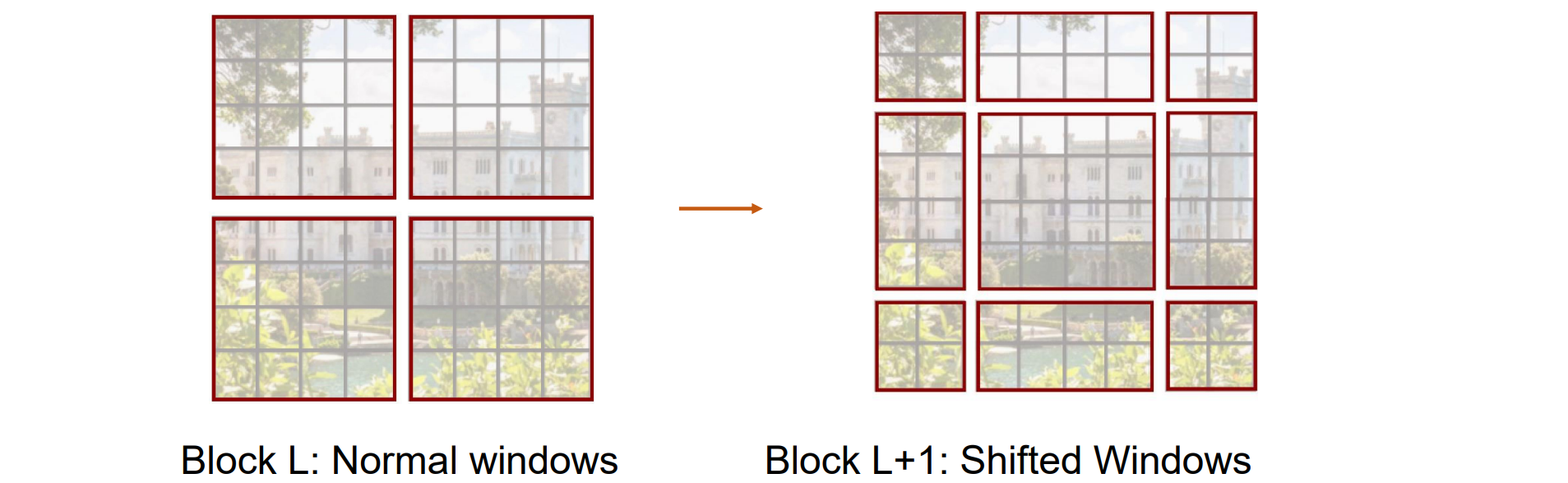
• 解决方法：在连续的 Transformer 块中交替使用普通窗口和移位窗口，更换窗口的划分形式，迭代几次

• ViT 为输入标记添加了位置嵌入，对图像中每个标记的绝对位置进行编码

• Swin 不使用全局位置嵌入，而是在计算注意力时对patches之间的相对位置进行编码

• Swin:

import torch
import torch.nn as nn
import torch.nn.functional as F
from torch import Tensor

# 定义基础的窗口注意力模块
class WindowAttention(nn.Module):
    def __init__(self, dim, num_heads, window_size, qkv_bias=True, attn_drop=0., proj_drop=0.):
        super().__init__()
        self.dim = dim
        self.num_heads = num_heads
        self.window_size = window_size
        self.qkv = nn.Linear(dim, dim * 3, bias=qkv_bias)
        self.attn_drop = nn.Dropout(attn_drop)
        self.proj = nn.Linear(dim, dim)
        self.proj_drop = nn.Dropout(proj_drop)
        self.softmax = nn.Softmax(dim=-1)

    def forward(self, x: Tensor, mask: Tensor = None) -> Tensor:
        B, N, C = x.shape  # B: batch size, N: number of tokens, C: channel dimension

        # 线性变换获取Q, K, V
        qkv = self.qkv(x).reshape(B, N, 3, self.num_heads, C // self.num_heads)
        qkv = qkv.permute(2, 0, 3, 1, 4)  # (3, B, num_heads, N, C // num_heads)
        q, k, v = qkv[0], qkv[1], qkv[2]

        # 窗口内的注意力计算
        attn = torch.matmul(q, k.transpose(-2, -1))  # (B, num_heads, N, N)
        attn = attn / (self.dim ** 0.5)  # 缩放

        if mask is not None:
            attn = attn + mask

        attn = self.softmax(attn)  # softmax得到概率分布
        attn = self.attn_drop(attn)

        # 加权求和
        out = torch.matmul(attn, v)  # (B, num_heads, N, C // num_heads)
        out = out.permute(0, 2, 1, 3).reshape(B, N, C)

        out = self.proj(out)
        out = self.proj_drop(out)

        return out


# 定义基础的Swin Transformer Block
class SwinTransformerBlock(nn.Module):
    def __init__(self, dim, num_heads, window_size, shift_size=0, mlp_ratio=4., qkv_bias=True, drop=0., attn_drop=0.):
        super().__init__()
        self.dim = dim
        self.window_size = window_size
        self.shift_size = shift_size

        # 窗口注意力层
        self.attn = WindowAttention(dim, num_heads, window_size, qkv_bias, attn_drop, drop)

        # MLP层
        self.mlp = nn.Sequential(
            nn.Linear(dim, int(dim * mlp_ratio)),
            nn.GELU(),
            nn.Linear(int(dim * mlp_ratio), dim)
        )
        self.drop = nn.Dropout(drop)

    def forward(self, x: Tensor) -> Tensor:
        # Layer Normalization + Attention
        x = x + self.attn(x)
        x = x + self.mlp(x)
        return x


# Patch Merging Layer
class PatchMerging(nn.Module):
    def __init__(self, dim, out_dim):
        super().__init__()
        self.proj = nn.Linear(dim * 4, out_dim)

    def forward(self, x: Tensor) -> Tensor:
        B, N, C = x.shape
        H = W = int(N ** 0.5)  # 假设输入是一个正方形的特征图
        x = x.view(B, H, W, C)  # (B, H, W, C)

        # 合并相邻的patches
        x0 = x[:, 0::2, 0::2, :]  # H/2, W/2
        x1 = x[:, 1::2, 0::2, :]  # H/2, W/2
        x2 = x[:, 0::2, 1::2, :]  # H/2, W/2
        x3 = x[:, 1::2, 1::2, :]  # H/2, W/2
        x = torch.cat([x0, x1, x2, x3], dim=-1)  # 合并四个部分

        x = x.view(B, -1, C * 4)  # 扁平化
        x = self.proj(x)
        return x


# Swin Transformer类
class SwinTransformer(nn.Module):
    def __init__(self, num_classes=1000, depths=[2, 2, 6, 2], embed_dim=96, num_heads=[3, 6, 12, 24], window_size=7, 
                 mlp_ratio=4., drop_rate=0., attn_drop_rate=0., patch_size=4):
        super().__init__()

        self.num_classes = num_classes
        self.depths = depths
        self.embed_dim = embed_dim
        self.window_size = window_size
        self.mlp_ratio = mlp_ratio
        self.drop_rate = drop_rate
        self.attn_drop_rate = attn_drop_rate
        self.patch_size = patch_size

        # Patch embedding
        self.patch_embed = nn.Conv2d(3, embed_dim, kernel_size=patch_size, stride=patch_size)

        # Swin Transformer Blocks
        self.blocks = nn.ModuleList()
        for i in range(len(depths)):
            block = nn.ModuleList()
            for _ in range(depths[i]):
                block.append(SwinTransformerBlock(
                    dim=embed_dim * (2 ** i),
                    num_heads=num_heads[i],
                    window_size=window_size,
                    shift_size=0 if i == 0 else window_size // 2,
                    mlp_ratio=mlp_ratio,
                    drop=self.drop_rate,
                    attn_drop=self.attn_drop_rate
                ))
            self.blocks.append(block)

        # Patch merging layers
        self.patch_merging = nn.ModuleList()
        for i in range(3):
            self.patch_merging.append(PatchMerging(embed_dim * (2 ** i), embed_dim * (2 ** (i + 1))))

        # Classification head
        self.norm = nn.LayerNorm(embed_dim * (2 ** 3))
        self.head = nn.Linear(embed_dim * (2 ** 3), num_classes)

    def forward(self, x: Tensor) -> Tensor:
        B = x.shape[0]
        x = self.patch_embed(x)  # Patch embedding

        # Swin Transformer Blocks
        for i, block in enumerate(self.blocks):
            for blk in block:
                x = blk(x)
            if i < 3:  # Patch merging after each stage
                x = self.patch_merging[i](x)

        x = x.mean(dim=1)  # global average pooling
        x = self.norm(x)
        x = self.head(x)  # classification head
        return x

# 示例使用：
if __name__ == "__main__":
    model = SwinTransformer(num_classes=1000)
    x = torch.randn(1, 3, 224, 224)  # 模拟输入的图片数据
    out = model(x)
    print(out.shape)  # 输出类别预测结果

---