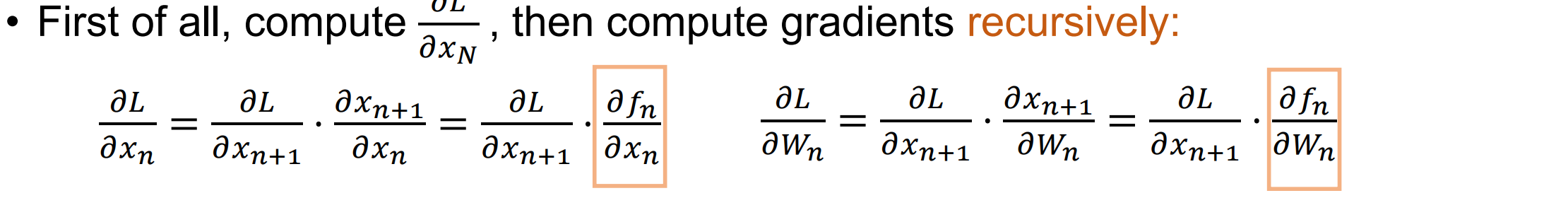Neural Networks as Computational Graphs

  • 有了梯度即可用SGD或AdamW优化器更新梯度训练neutral network,关键问题是如何计算梯度

  • 神经网络可以看作是有向无环计算图

  • 每个节点代表一个函数，每条边代表一个特征

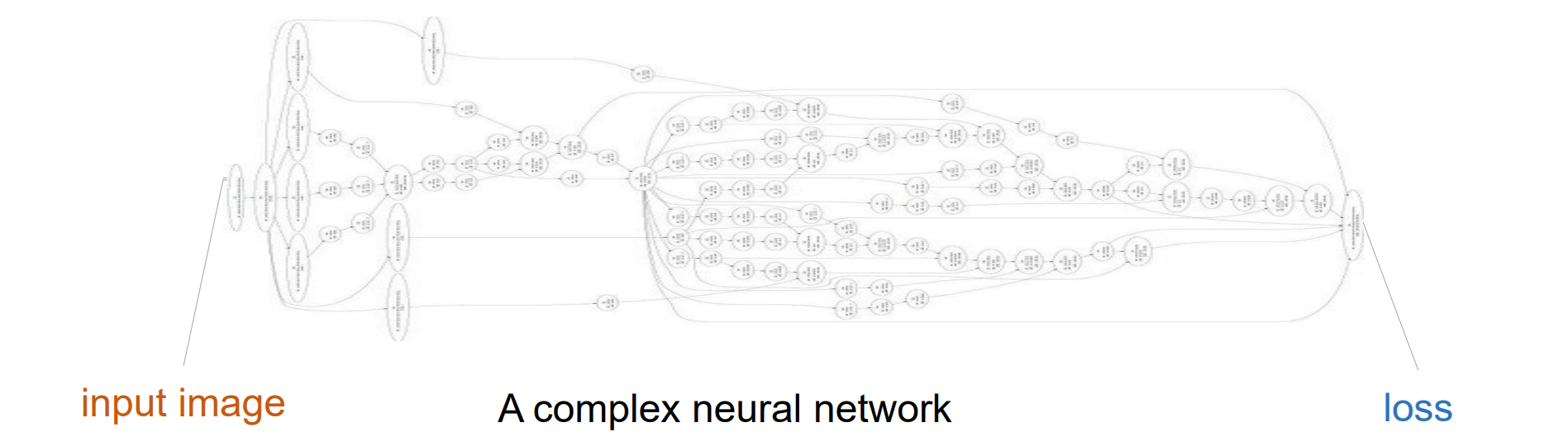
image.png

  • 任何神经网络可以画成如下形式的计算图，左侧是输入图像，中间是神经网络而右侧得到损失

image.png

Back Propagation

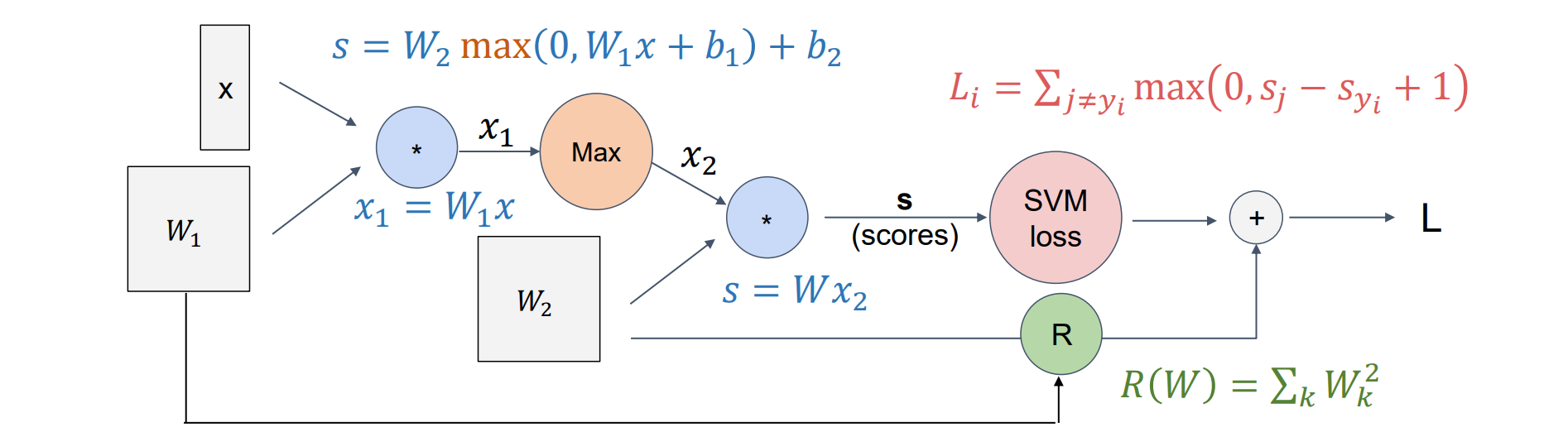
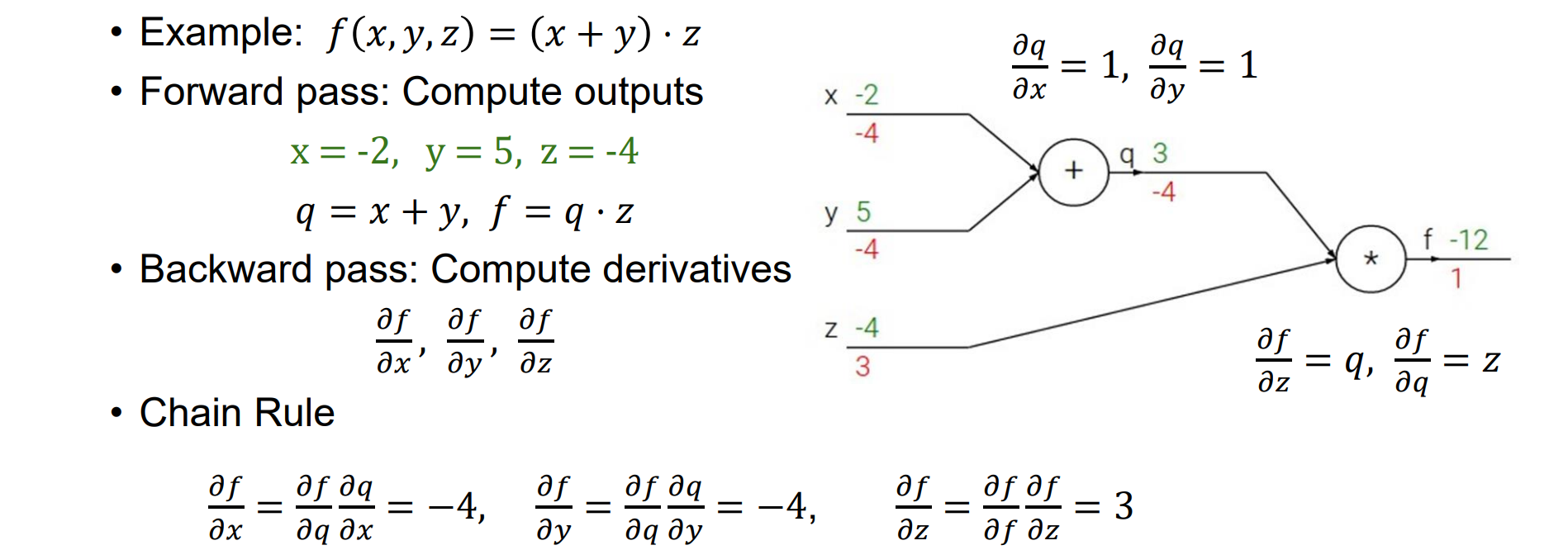
  • 先考虑一个结点：

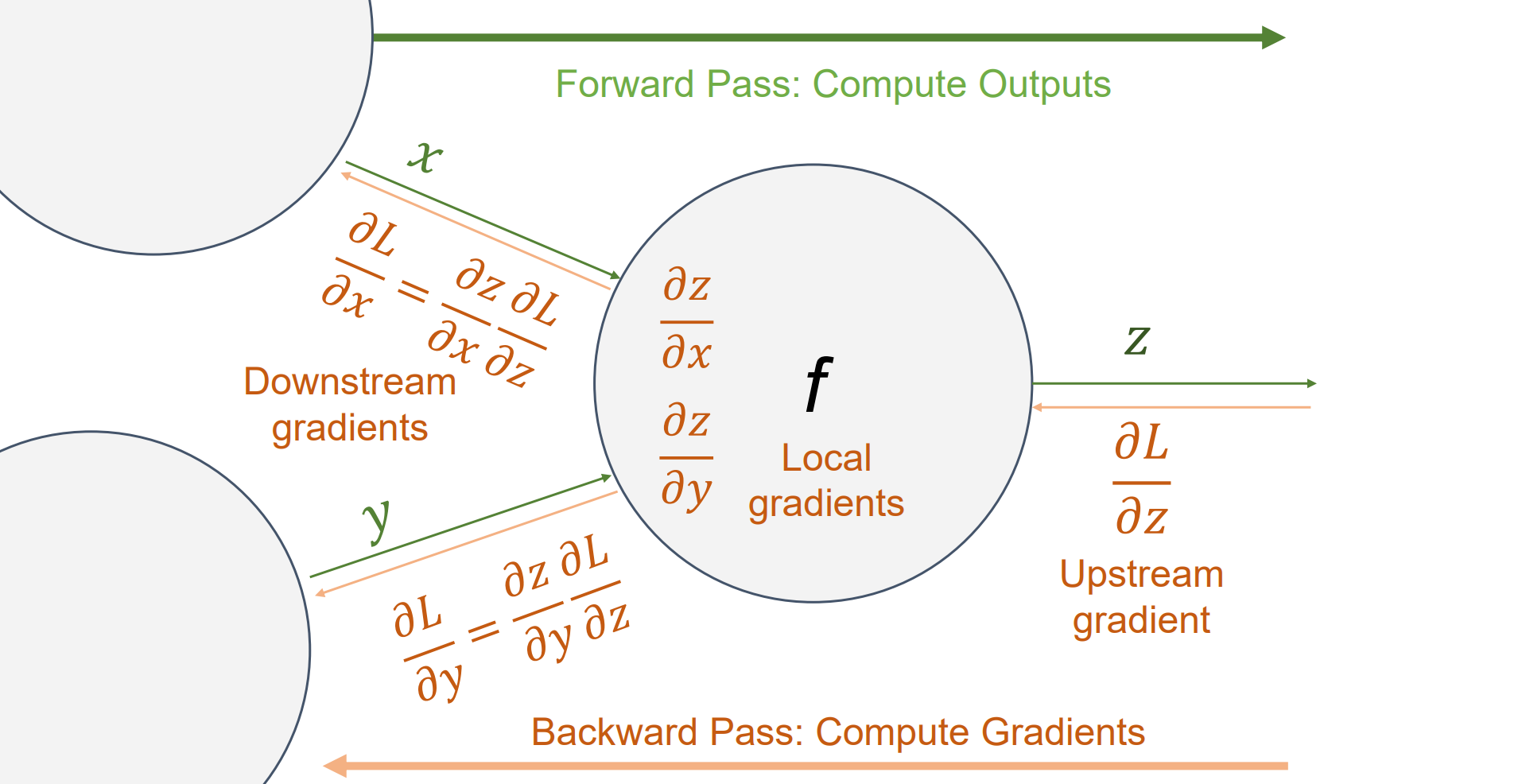
image.png

  • 反向传播：从输出端反传到输入端，计算思路：

    1. 先写前向运算的计算图
    2. 算forward，并且算出loss
    3. 从后往前计算梯度，利用链式法则

  • 可以认为loss函数的上游梯度为1

image.png

  • 可以对部分计算进行合并，例如画框的部分可以合并为sigmoid函数，合并的过程又称神经网络编译

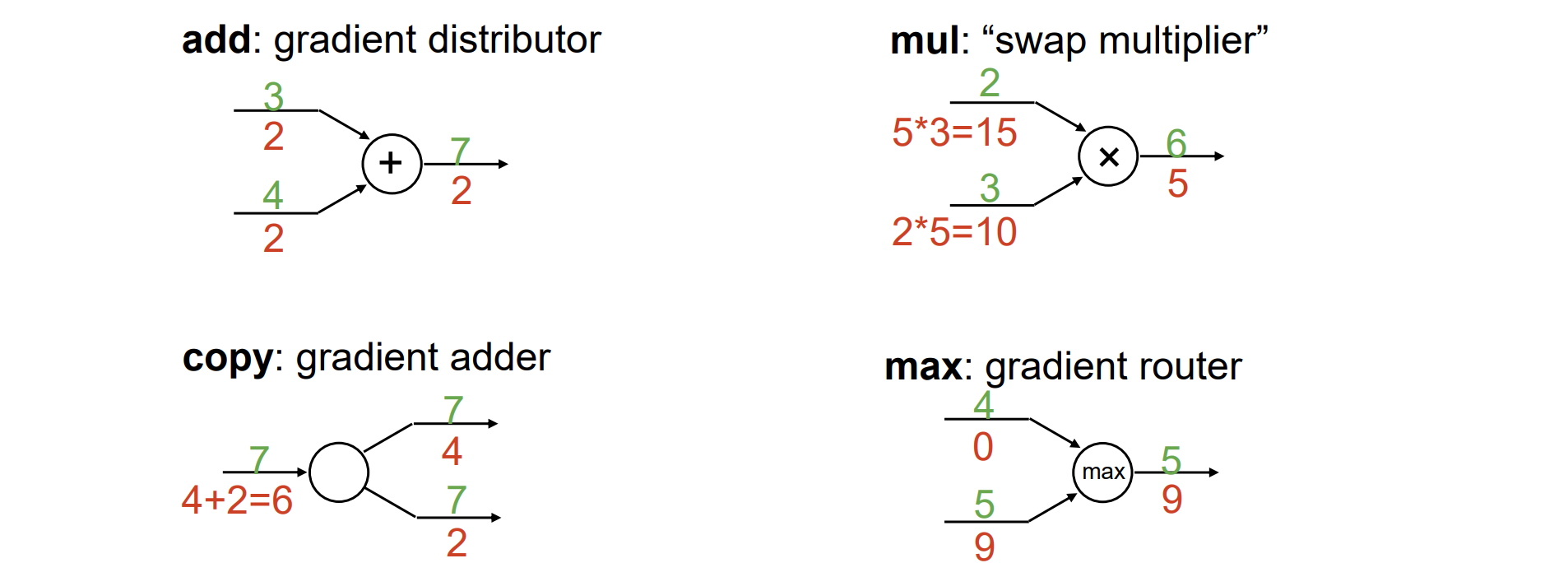
image.png

Common Patterns in Gradient Flow

  • +：直接反传

  • *：反乘

  • 复制：反加

  • max：沿着大的分支传回，小的置0

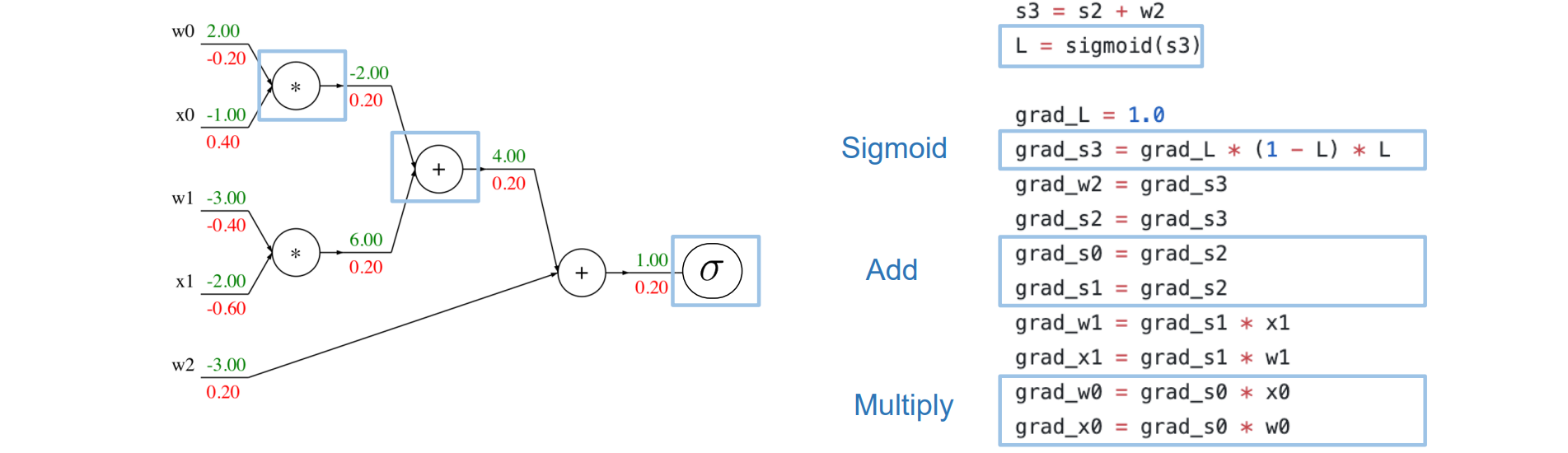
image.png

Back Propagation: Flat Implementation

  • 在定义前向计算时显式写入后向计算，例如：

image.png

Back Propagation: Auto Differentiation

  • 步骤思路：

    1. 构建计算图
    2. 运行正向计算
    3. 对所有图节点执行拓扑排序
    4. 通过反向计算图自动运行向后传递

  • 做拓扑排序可以构建任务依赖关系，可以进行自动构建

image.png

Back Propagation with Tensors

  • 对于𝑥 ∈ ℝ𝑁, 𝑦 ∈ ℝ，导数是梯度，n维；对于𝑥 ∈ ℝ𝑁, 𝑦 ∈ ℝM，导数为Jacobian矩阵，梯度是nxm维

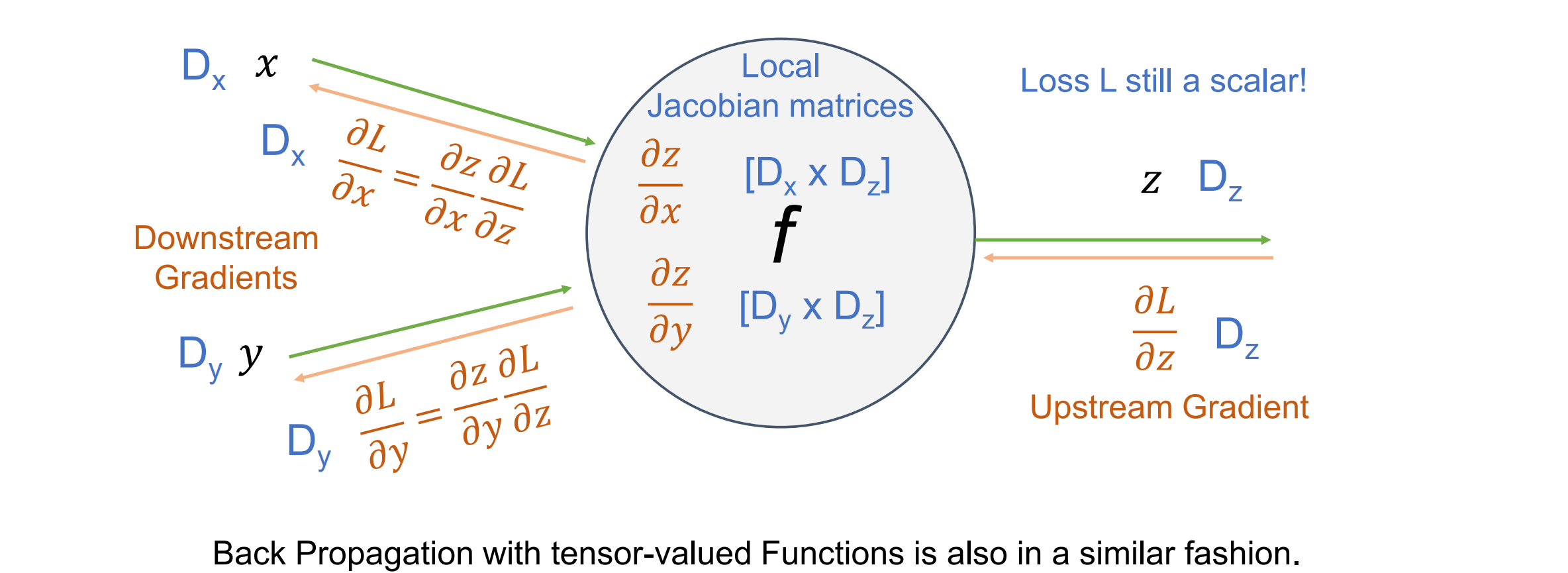
image.png

  • tips：更新梯度计算公式的时候可以先看形状，然后根据形状凑w和x的位置以及是否有转置

image.png

Back Propagation for Higher-Order Derivatives

  • 计算高阶导数的时候需要先把整个计算图存储下来，再对整个计算图再做一次back propagation

  • back propagation：用递归的链式法则进行更新定义

image.png