Linear Classifiers的局限性

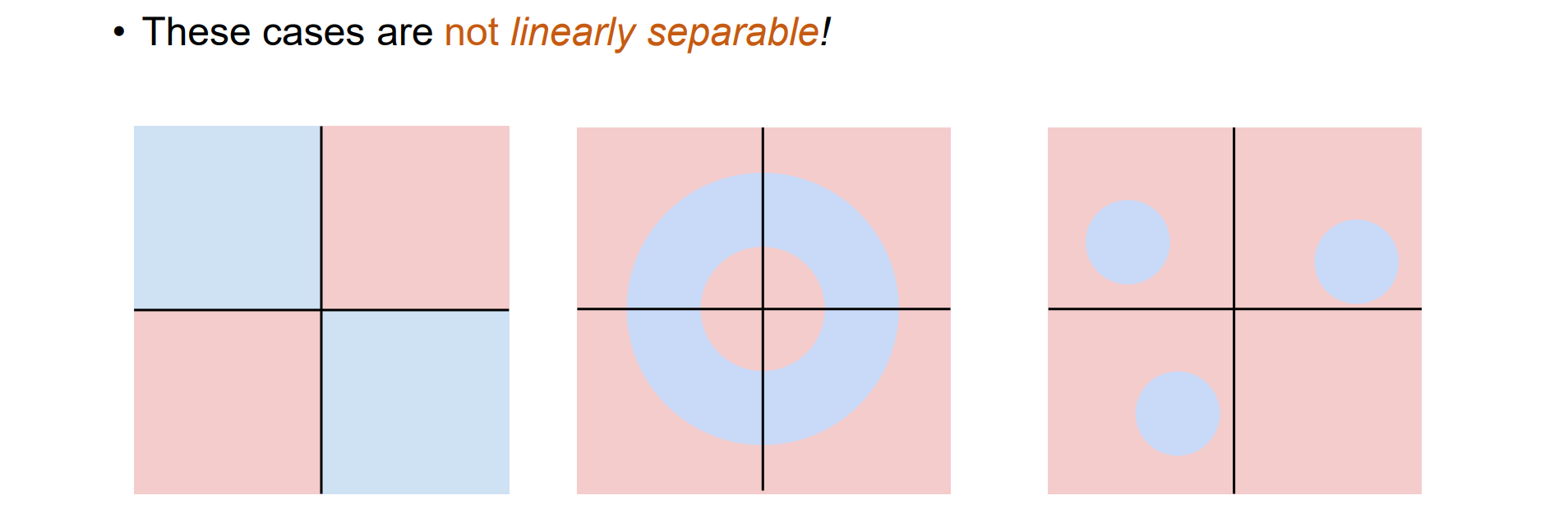
  • Linear Classifiers无法解决线性不可分的问题：

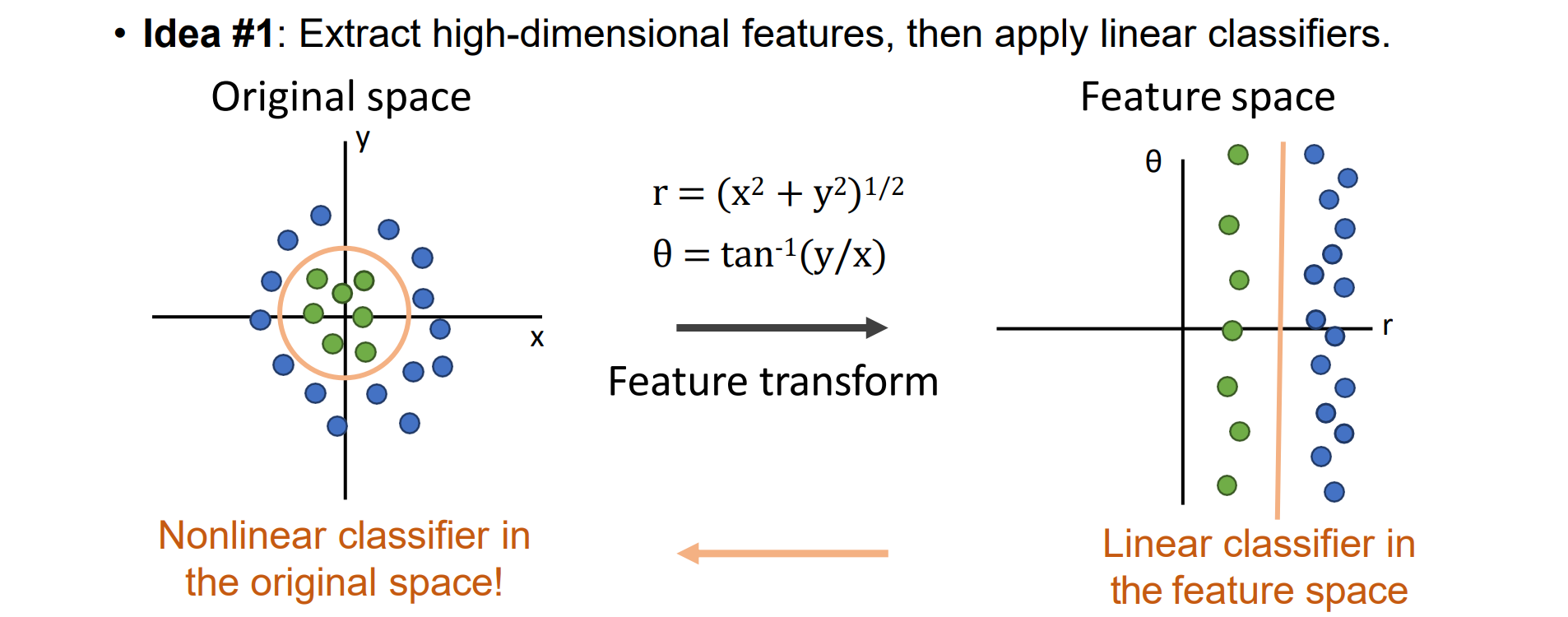
image.png

  • Idea #1:将低维特征进行高维非线性的特征变换从而得到高维的线性可分

image.png

  • Idea #2:HoG for Linear Classifier：
    1. 将图像分成8x8的区域
    2. 对每个区域计算梯度直方图
    3. 使用SVM作为分类器

image.png

  • HoG方法可以很好的描述图像内容并且丢弃不重要的内容，对小变化具有鲁棒性

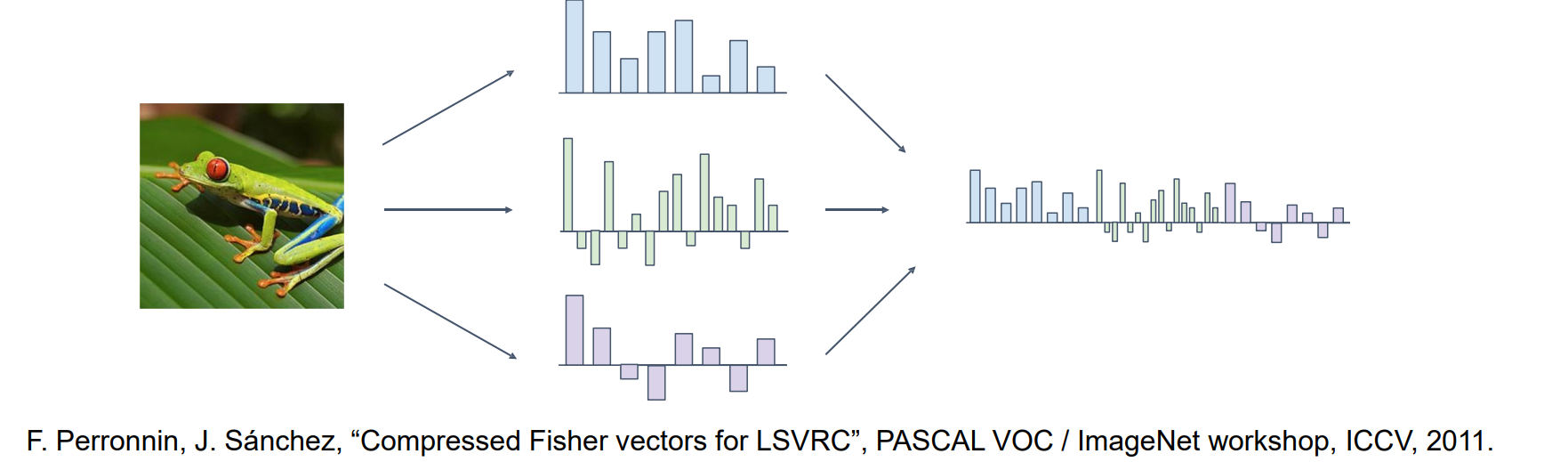
  • Idea #3:线性分类器的高维特征压缩：提取多个feature图，拼在一起映射到高维空间，再用PCA降维

    1. 连接多个图像特征：维度越高越好
    2. 使用 PCA 压缩并提取 Fisher 向量以减小维度
    3. 使用 SGD 进行一对多 SVM 学习

image.png

Neural Networks

Single-Layer Perceptron

  • 单层感知机SLP无法解决一些非常简单的问题(XOR)，点乘完后激活从而完成分类任务

  • Contributed to the so-called AI winter.(不能解决异或问题)

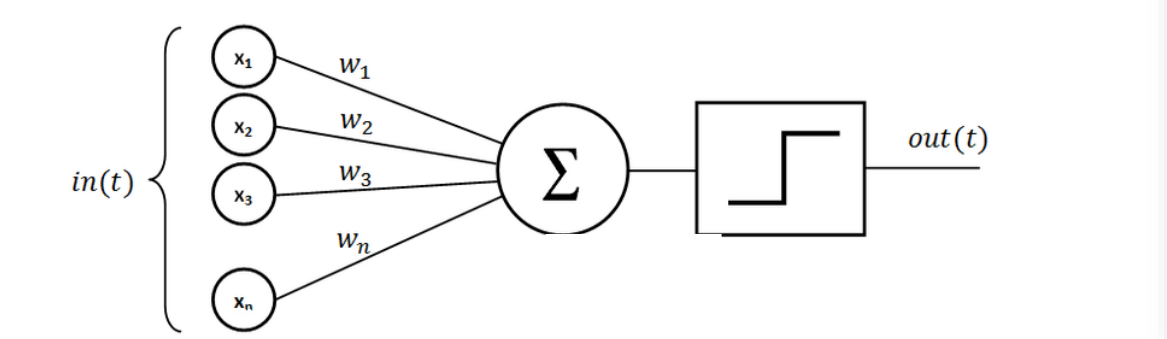
image.png

Multiple Layer Neural Networks

  • MLP至少有一个隐藏层，可以近似任意精度的任何函数

  • MLP只是一种神经网络

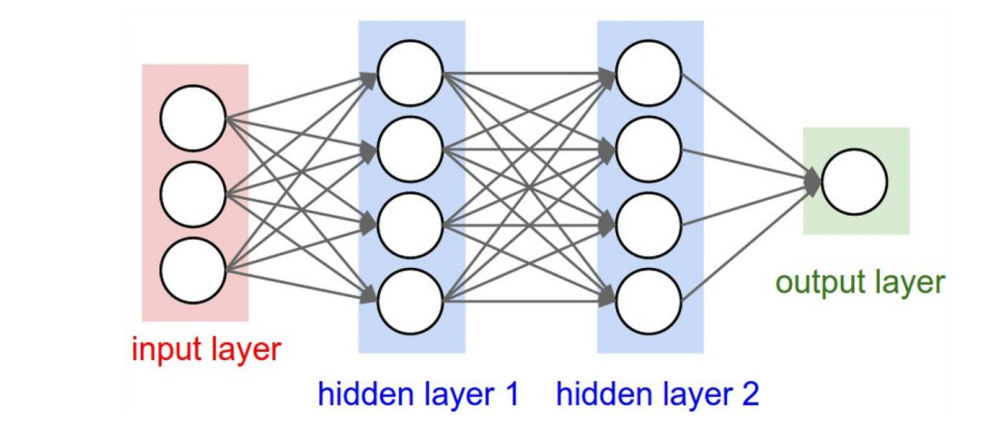
image.png

  • 2-layer Neural Networks (MLPs):𝑠 = W2𝝈 (𝑊1𝑥) , 𝑊1 ∈ ℝ𝐻×𝐷, 𝑊2 ∈ ℝ𝐶×H，其中H 是隐藏神经元的数量，σ 是非线性激活函数

  • 激活函数𝝈必须是非线性的，且必须是可微的

  • MLPs可以逼近任何函数的原理：两个sigmoid加入偏置可以组成任何基函数，多层MLPs可以用多个基函数局部逼近任何函数，再拼成一个完整的逼近函数

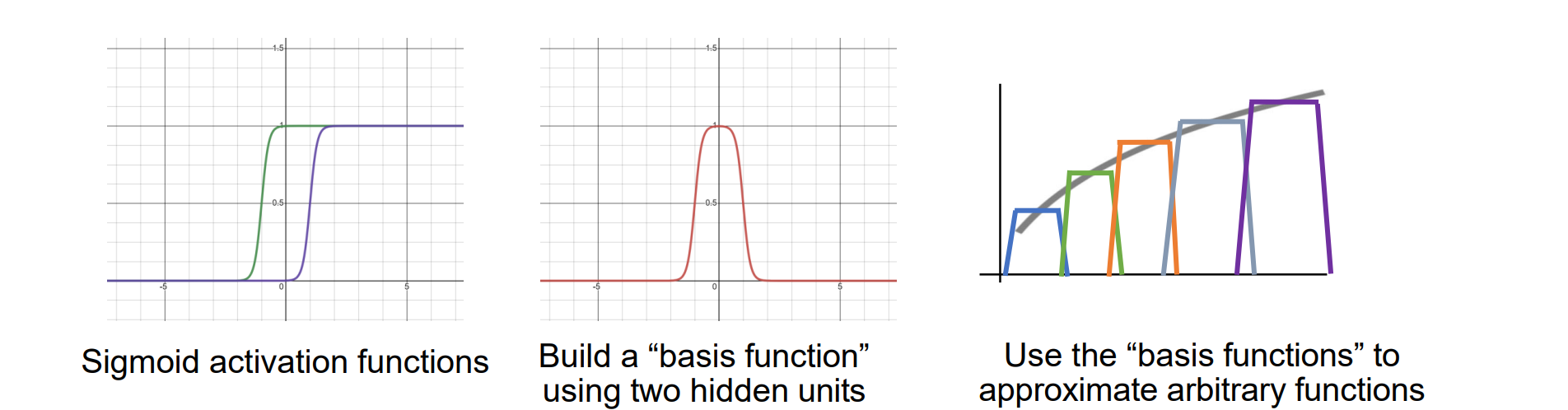
image.png

激活函数

image.png

  • 组合后可以逼近任何其他函数

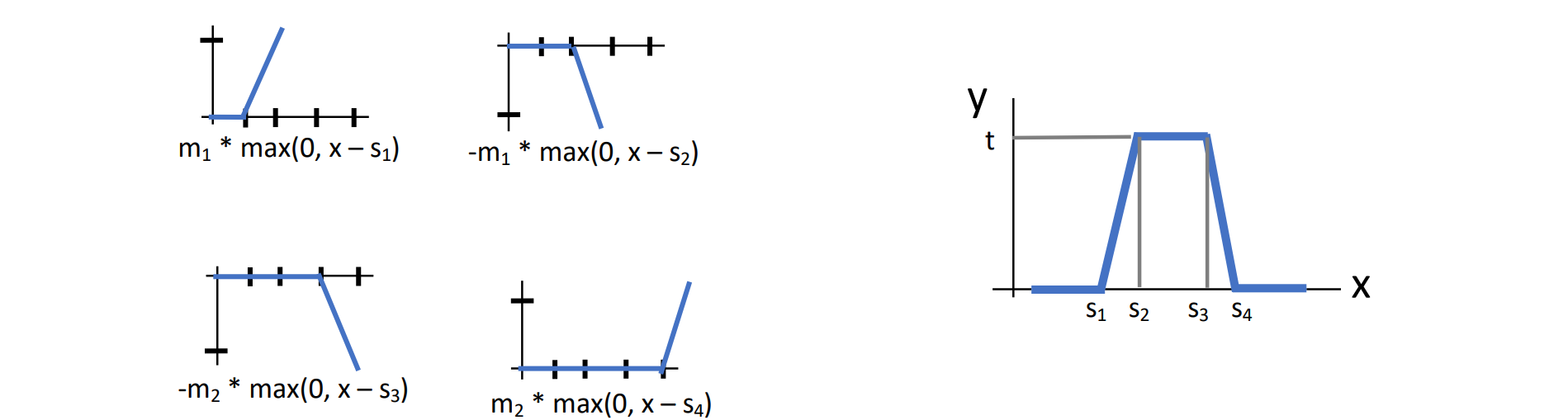
image.png

Neural Networks: Visual Viewpoint

  • MLPs可以为每类形成多个模板，w2可以理解为模板的线性组合

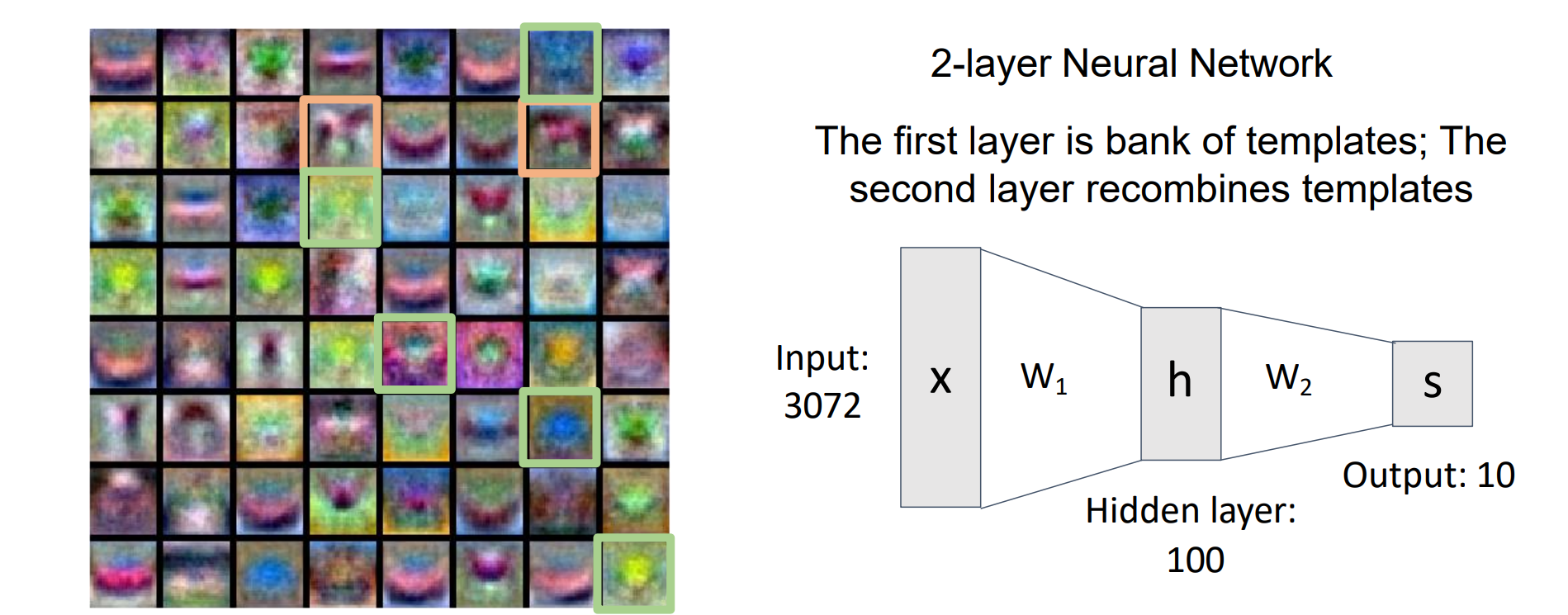
image.png

Neural Networks: Geometric Viewpoint

  • MLPs提供了更复杂的决策面，提高了非线性性

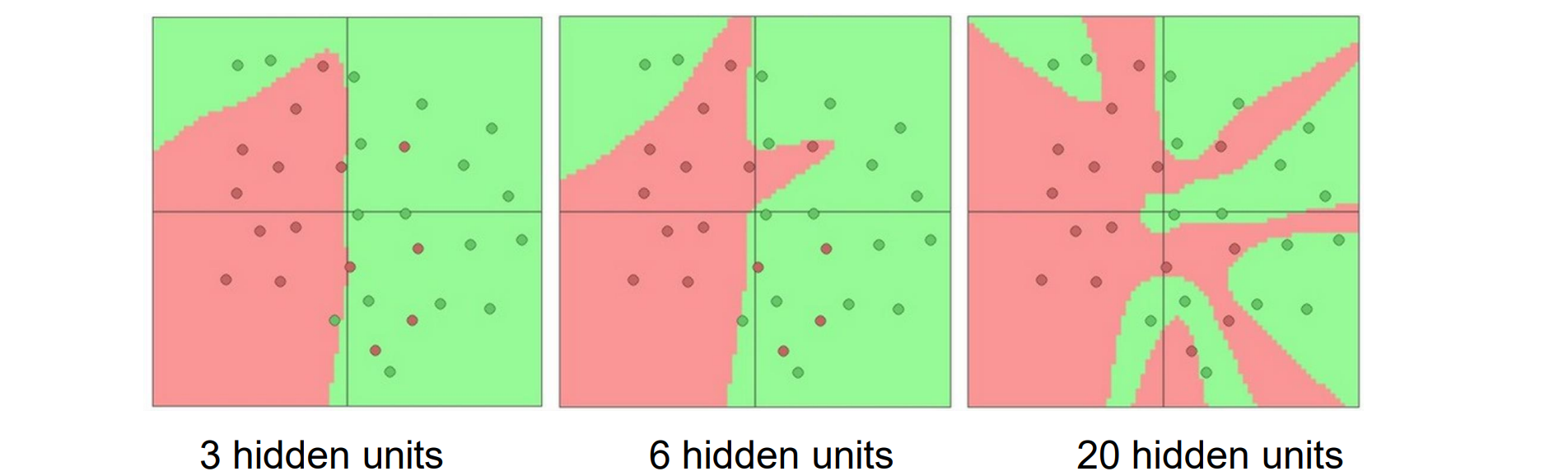
image.png

Deep Neural Networks

  • MLPs的局限性：MLPs前提假设必须有大量的隐藏层才能逼近其他复杂函数，从而使得深度变深，复杂性提高

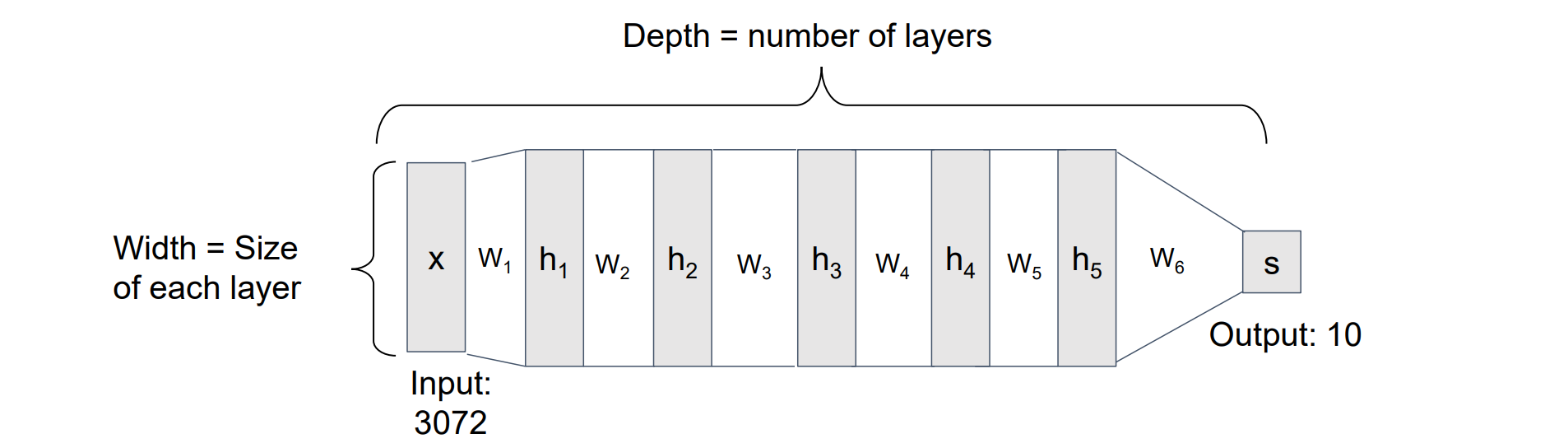
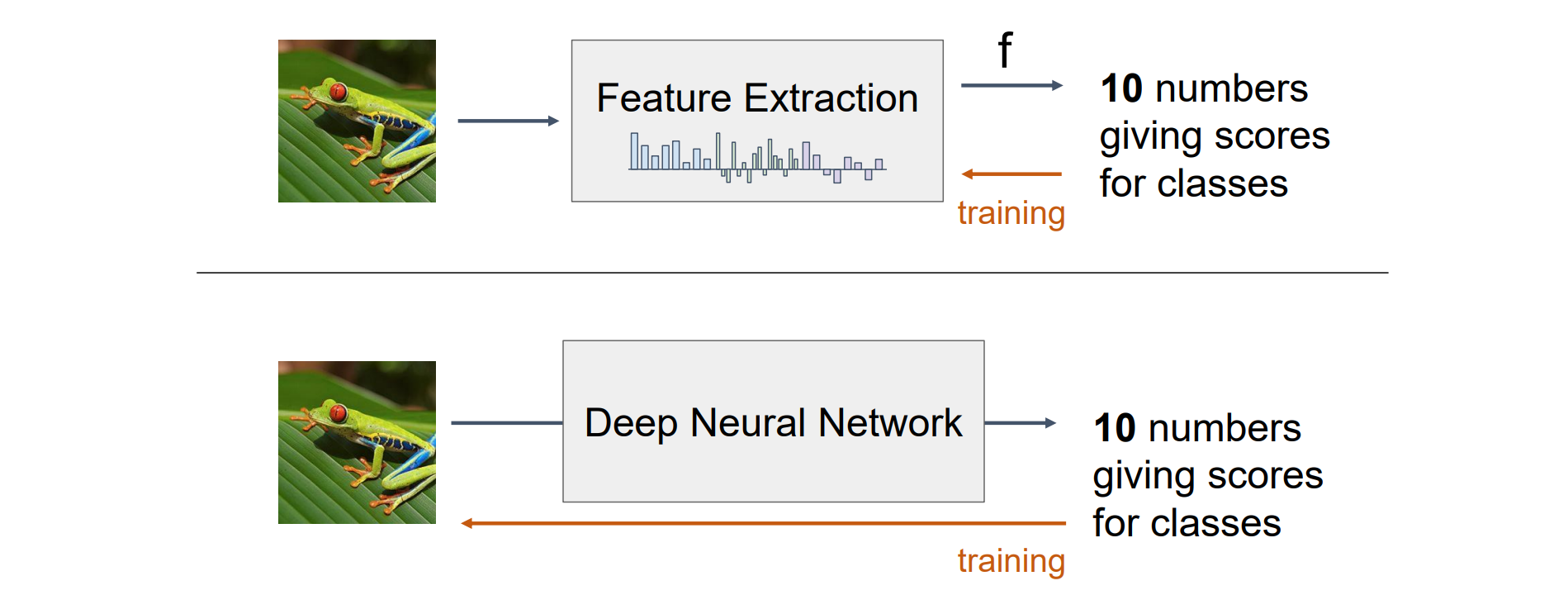
image.png

Neural Networks vs Image Features

  • Feature Extraction是手动提取特征然后应用线性分类器，而Deep Neutral Network是自动特征提取，实现了端对端

image.png